太阳光入射角差异对不同气候区立面垂直安装光伏组件发电量的影响研究

叶 露，何 涛,2*，张昕宇，孙峙峰，李博佳，王 敏

(1. 中国建筑科学研究院有限公司，北京 100013；2. 国家建筑工程技术研究中心，北京 100013)

0 引言

截至2020年，中国光电建筑应用装机容量已超过30 GW，光电建筑应用面积占既有建筑总面积的约1%，主要以工商业屋顶应用为主。经测算，中国现有建筑中，可以安装光伏组件的所有建筑立面面积与屋顶面积相当[1]，而在立面上安装光伏组件的节能潜力较大，这也是零能耗建筑发展的必然方向[2]。但是立面安装的光伏组件的安装倾角、方位角受建筑外围护结构的限制，与地面最佳倾角安装的光伏组件相比，二者的全年太阳光入射角的变化差异较大，导致全年发电量也有所不同。

太阳光入射角直接影响单块太阳电池的实际输出功率，进而会影响整个光伏组件的实际输出功率。屠佳佳等[3]的研究结果表明：在同一时刻改变光伏组件的安装倾角和方位角，其发电效率也会随之发生微小的变化。行业普遍采用入射角修正系数(IAM)来表示光线透过光伏组件表面时产生的损失比率，入射角修正模型主要包括美国桑迪亚国家实验室提出的IAM测算模型[4]，以及常用的ASHRAE模型及菲涅尔模型。

立面安装包括立面垂直安装和立面倾斜安装两种方式，本文研究仅针对立面垂直安装。基于入射角修正模型的ASHRAE模型，本文对中国不同气候区立面垂直安装的光伏组件发电量和地面最佳倾角安装的光伏组件发电量进行了计算和差异对比，计算二者的相对偏差并得出量化值，最终直观得到太阳光入射角差异对立面垂直安装的光伏组件发电量与地面最佳倾角安装光伏组件发电量的差值的影响。

1 建立光伏组件发电量计算模型

立面垂直安装光伏组件的发电量计算过程与地面最佳倾角安装光伏组件的不同，其需要同时考虑安装方式和环境参数的影响。立面垂直安装光伏组件的发电量计算过程主要分为3个部分：倾斜表面接收的太阳辐照度计算、修正系数计算、光伏组件发电量计算，下面进行具体分析。

1.1 倾斜表面接收的太阳辐照度计算

立面垂直安装光伏组件表面接收的太阳辐照度的计算过程与地面最佳倾角安装光伏组件的相同。立面垂直安装光伏组件表面接收的太阳辐照度GT为光伏组件倾斜表面接收的直射太阳辐照度ID,θ、散射太阳辐照度Id,θ及反射太阳辐照度IR,θ之和，即：

式中：ID,H为水平面接收的直射太阳辐照度，W/m2；Id,H为水平面接收的散射太阳辐照度，W/m2；θ为太阳光入射角，(° )；αs为太阳高度角，(° )；S为光伏组件安装倾角，立面垂直安装时取90°；ρG为反射率。

1.2 修正系数计算

光伏组件盖板玻璃对入射的太阳辐照具有反射和吸收等作用，太阳光入射角不同时，其透射吸收比也不同，所以需要通过公式计算入射角修正系数IAM(θ)。入射角修正系数可表示为：

式中：b0为经验参数，由光伏组件的类型决定，一般取0.05。

在不同的环境参数下，光伏组件工作温度是变化的，而工作温度的变化对于光伏发电系统效率的影响较大，因此，需要考虑不同工作温度下的温度修正系数。温度修正系数XT的计算式可表示为：

式中：EffT为光伏组件的温度系数，/℃，其取值由光伏组件的类型决定，可通过厂家提供的样本获得；TPV为光伏组件工作温度，℃。

1.3 光伏组件发电量计算

发电量是输出功率在时间范围内的积分，求得光伏组件的输出功率，即可得到光伏组件的发电量。光伏组件的输出功率与光伏组件有效面积、光伏组件的光电转换效率、太阳辐照度、光伏组件工作温度等有关。光伏组件输出功率P的计算式可表示为：

式中：APV为光伏组件的有效面积，m2；ηPV为标准测试条件(STC)下光伏组件的光电转换效率。

2 不同气候区立面垂直安装光伏组件的发电量对比

由于地理纬度存在差异，不同地区立面垂直安装光伏组件的太阳光入射角会随之变化。由于太阳光入射角存在差异，导致在不同地区立面垂直安装光伏组件的年发电量与地面最佳倾角安装光伏组件之间的差异也会不同。

本文选取中国4个不同的气候区，从北至南分别在4个气候区中选取哈尔滨市、北京市、上海市、广州市作为4个典型城市进行分析。4个典型城市的纬度分别约为 44°、40°、30°、22°，依次递减，根据天体运动规律可计算得到不同气候区、不同光伏组件安装方式下太阳光入射角的变化情况；并利用前文所述公式，分析不同气候区立面垂直安装光伏组件年发电量与地面最佳倾角安装光伏组件年发电量之间的差异。4个典型城市的地理位置及气候条件如表1所示。

表1 4个典型城市的地理位置及气候条件Table 1 Geographical location and climatic conditions of four typical cities

对于地面最佳倾角安装的光伏组件，其最佳倾角通常等于当地纬度，因此，在哈尔滨市、北京市、上海市、广州市以地面最佳倾角安装光伏组件时，其最佳倾角分别为 44°、40°、30°、22°；而在立面垂直安装时，光伏组件安装倾角为90°。

2.1 不同气候区太阳光入射角的变化

中国地处北半球，在夏至日时太阳光直射北回归线，太阳高度角在正午(12:00)时最高。但是随着纬度的增加，同一时刻下的太阳高度角越来越小。根据天体的运动规律及相关公式，可计算得到夏至日时不同地区立面垂直安装光伏组件的太阳光入射角，然后与地面最佳倾角安装光伏组件的太阳光入射角进行对比，可得到不同光伏组件安装方式下太阳光入射角的变化情况。夏至日时，4个典型城市不同光伏组件安装方式下太阳光入射角的变化曲线如图1所示。图中：绿色直线为太阳光入射角为90°时的标准线。

图1 夏至日时，4个典型城市不同光伏组件安装方式下太阳光入射角的变化曲线Fig. 1 Variation curve of sunlight incidence angle under different PV modules installation modes in four typical cities during summer solstice

由图1可知：无论安装城市如何变化，立面垂直安装光伏组件的太阳光入射角均高于地面最佳倾角安装光伏组件的太阳光入射角，且随着光伏组件安装城市纬度的降低，二者之间的差值逐渐增加。夏至日时，从太阳升起到落下，在哈尔滨市、北京市、上海市、广州市两种不同光伏组件安装方式下太阳光入射角的差值分别在11.9°～45.6°、11.8°～45.8°、13.2°～60.0°、16.9°～67.2°之间变化。

而当太阳光入射角大于等于90°时，意味着太阳光与光伏组件表面平行或照射到光伏组件背面，在这种情况下，光伏组件表面可接收的直射太阳辐照度被大幅削弱。同时，当太阳光入射角过大时(尤其是大于70°以后)，会极大地影响光伏组件的输出参数值，此时的入射角修正系数也会迅速降低，不利于光伏组件发电。因此，研究不同光伏组件安装方式下因太阳光入射角差异而引起的发电量变化，对于指导不同气候区立面垂直安装的光伏发电系统的设计意义重大。

2.2 不同气候区的光伏组件发电量变化

根据2020年哈尔滨市、北京市、上海市、广州市4个典型城市的天气条件，可得到4个典型城市不同安装方式下光伏组件月发电量的变化情况，具体如图2～图5所示。

图2 哈尔滨市不同安装方式下光伏组件月发电量对比Fig. 2 Comparison of monthly power generation capacity of PV modules under different installation modes in Harbin

图3 北京市不同安装方式下光伏组件月发电量对比Fig. 3 Comparison of monthly power generation capacity of PV modules under different installation modes in Beijing

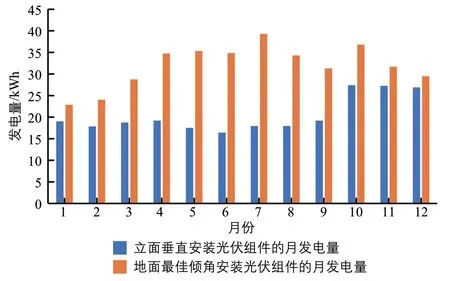
图4 上海市不同安装方式下光伏组件月发电量对比Fig. 4 Comparison of monthly power generation capacity of PV modules under different installation modes in Shanghai

图5 广州市不同安装方式下光伏组件月发电量对比Fig. 5 Comparison of monthly power generation capacity of PV modules under different installation modes in Guangzhou

由图2可知：在1—2月及11—12月时，哈尔滨市立面垂直安装光伏组件的月发电量高于地面最佳倾角(为44°)安装光伏组件的月发电量。在3—10月时情况相反，尤其是在5—7月时，太阳运动到北回归线附近，立面垂直安装光伏组件的月发电量会迅速下降，与地面最佳倾角安装光伏组件的月发电量之间的差值也越大；在6月时二者的差值达到最大，为19.54 kWh。

由图3可知：在1月和12月时，北京市立面垂直安装光伏组件的月发电量比地面最佳倾角(为40°)安装光伏组件的月发电量高；在2—11月时情况相反。在6月时，立面垂直安装光伏组件的月发电量为23.89 kWh，比地面最佳倾角安装光伏组件的月发电量低了21.0 kWh。

由图4可知：由于纬度较低，在1—12月期间，上海市立面垂直安装光伏组件的月发电量均比地面最佳倾角(为30°)安装光伏组件的月发电量低。在7月时，立面垂直安装光伏组件的月发电量为17.9 kWh，地面最佳倾角安装光伏组件的月发电量为39.3 kWh，此时二者的差值达到最大，为 21.4 kWh。

由图5可知：与上海市的情况类似，在1—12月期间，广州市立面垂直安装光伏组件的月发电量均比地面最佳倾角(为22°)安装光伏组件的月发电量低。在7月时，立面垂直安装光伏组件的月发电量为15.3 kWh，地面最佳倾角安装光伏组件的月发电量为31.8 kWh，此时二者的差值达到最大，为16.5 kWh。

地理位置不同，不同安装方式下光伏组件的发电量变化情况不同，需要引入相关系数来量化同一地区立面垂直安装和地面最佳倾角安装的光伏组件发电量之间的差异。本文选择采用相对偏差来衡量不同安装方式下光伏组件的发电量差异，最后可计算得到2020年4个气候区不同安装方式下光伏组件年发电量的相对偏差。

相对偏差β的计算式可表示为：

式中：N为计算小时数，h；P90为立面垂直安装时光伏组件的输出功率，W；Pφ为光伏组件最佳安装倾角为φ时以地面最佳倾角安装的光伏组件的输出功率。

当相对偏差大于零时，说明立面垂直安装光伏组件的发电量低于地面最佳倾角安装光伏组件的发电量；当相对偏差小于零时，说明立面垂直安装光伏组件的发电量高于地面最佳倾角安装光伏组件的发电量。

根据式(8)，可计算得到2020年哈尔滨市、北京市、上海市、广州市4个典型城市不同安装方式下光伏组件年发电量的相对偏差，结果如图6所示。

由图6可知：随着所在地区纬度的降低，不同安装方式下光伏组件年发电量的相对偏差逐渐增加，由21%增加到40%。由此可知，低纬度地区受太阳高度角的影响较大，因此与地面最佳倾角安装光伏组件的发电量相比，立面垂直安装光伏组件的发电量减少得更多；这也意味着相同安装面积(即光伏组件有效面积总和)的情况下，低纬度地区立面垂直安装的光伏组件全年发电量更少，并且与地面最佳倾角安装的光伏组件发电量之间的差值更大，因此，该类地区光伏组件不建议采用立面垂直安装方式。

图6 4个典型城市不同安装方式下光伏组件年发电量的相对偏差Fig. 6 Relative deviation of annual power generation capacity of PV modules under different installation modes in four typical cities

根据式(8)，计算哈尔滨市、北京市、上海市、广州市4个典型城市不同安装方式下光伏组件月发电量的相对偏差情况，具体结果如表2所示。

表2 4个典型城市不同安装方式下光伏组件月发电量的相对偏差情况Table 2 Relative deviation of monthly power generation capacity of PV modules under different installation modes in four typical cities

由表2可知：在哈尔滨市、北京市、上海市、广州市4个典型城市，不同安装方式下光伏组件月发电量的相对偏差经历了逐渐增加，达到峰值后再逐月下降的过程。在哈尔滨市和北京市，均存在光伏组件月发电量的相对偏差小于零的情况，即立面垂直安装光伏组件的月发电量高于地面最佳倾角安装光伏组件的月发电量。然而，随着光伏组件安装城市纬度的降低，在上海市和广州市，光伏组件月发电量的相对偏差均大于零，意味着立面垂直安装光伏组件的月发电量均小于地面最佳倾角安装光伏组件的月发电量。哈尔滨市、北京市、上海市、广州市光伏组件月发电量的最大相对偏差分别为44.7%、48.1%、54.4%、56.2%，可以看出，在低纬度地区，光伏组件月发电量的相对偏差大于50%，说明立面垂直安装光伏组件的月发电量比地面最佳倾角安装光伏组件的月发电量减少了一半以上。

3 实验验证

为了验证前文不同安装方式下光伏组件发电量变化情况的分析结论，于2020年7月20日在北京市进行了对比实验。实验选择两块型号相同的光伏组件，安装倾角分别设置为40°和90°；两块光伏组件均无阴影遮挡。实验中部分设备的名称及其参数如表3所示。

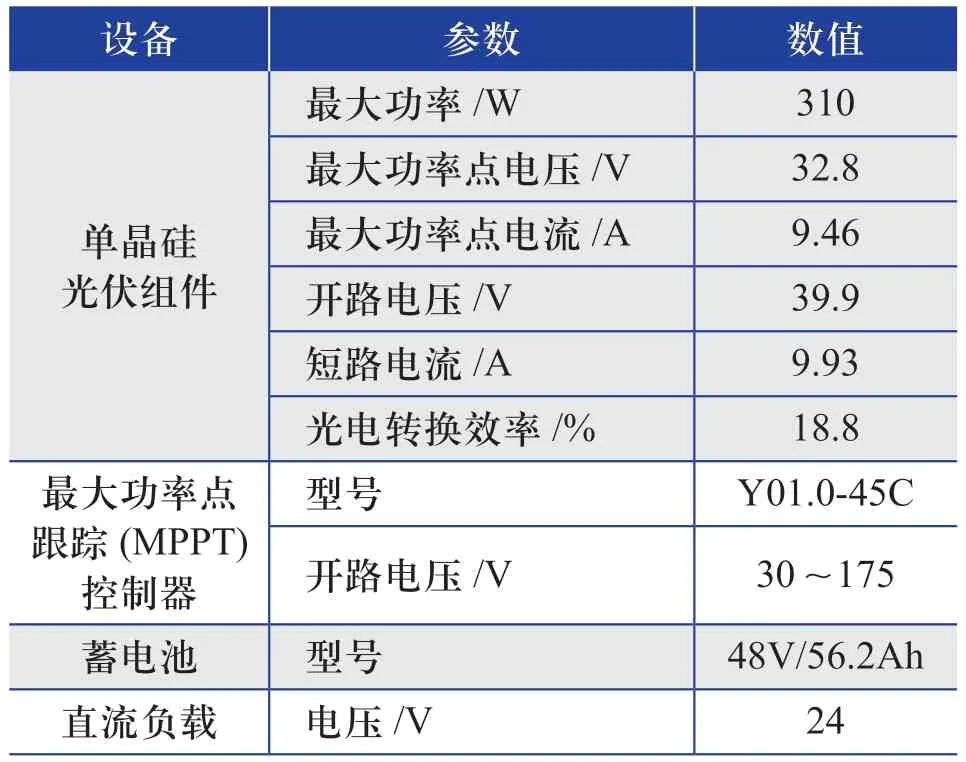
表3 实验中部分设备的名称及其参数Table 3 Names and parameters of some equipment in the experiment

该实验选择直流负载蓄电池使用型系统，由光伏组件、蓄电池组、充放电控制器(具备MPPT)，以及直流负载等组成。蓄电池组用来存储白天光伏组件产生的电能，以供直流负载使用。直流负载蓄电池使用型系统的原理图如图7所示。

图7 直流负载蓄电池使用型系统的原理图Fig. 7 Principle diagram of DC load battery service system

不同安装方式的光伏组件发电量测试平台如图8所示。将两块光伏组件同时放置在同一室外环境中，其中一块光伏组件采用立面垂直安装方式，垂直安装在建筑南立面；另一块光伏组件以地面最佳安装倾角40°放置在旋转台上，调整旋转台朝向为正南向。保证2块光伏组件的外接负载相同，通过数据采集仪记录2块光伏组件的小时输出功率数据，对比二者的小时输出功率差值，并比较二者的相对偏差大小。

图8 不同安装方式的光伏组件发电量测试平台Fig. 8 Power generation capacity test platform of PV modules with different installation modes

4 结果分析

通过实验数据与计算结果的对比，可得到立面垂直安装光伏组件的小时输出功率和地面最佳倾角(为40°)安装光伏组件的小时输出功率差异，具体结果如图9所示。

图9 不同安装方式下光伏组件的小时输出功率差异Fig. 9 Difference of hourly output power of PV modules under different installation modes

由图9可知：由于受太阳光入射角的影响，立面垂直安装光伏组件的小时输出功率低于地面最佳倾角(为40°)安装光伏组件的小时输出功率，两种安装方式下光伏组件的小时输出功率差值在14:00达到最大，为95.2 W。

根据实验结果，计算得到两种安装方式下光伏组件小时输出功率的相对偏差，结果如图10所示。

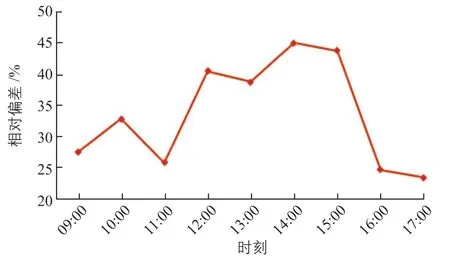
图10 两种安装方式下光伏组件小时输出功率的相对偏差Fig. 10 Relative deviation of hourly output power of PV modules under two installation modes

由图10可知：光伏组件小时输出功率的相对偏差在14:00达到最大，约为45%。

根据图10，可计算得到光伏组件日发电量的相对偏差约为37.6%。通过式(1)～式(8)，可计算得出7月20日光伏组件日发电量的相对偏差约为36.6%。二者的相对误差为2.49%，误差较小。证明采用本文提出的相对偏差计算公式表征立面垂直安装和地面最佳倾角安装的光伏组件发电量之间的差异较为准确。

5 结论

本文基于入射角修正模型，探讨了太阳光入射角差异对不同气候区立面垂直安装光伏组件发电量的影响，对不同气候区因太阳光入射角差异而引起的立面垂直安装光伏组件的发电量和地面最佳倾角安装光伏组件的发电量之间的差异进行了分析和对比，并计算了二者的相对偏差。研究结果显示：

1)立面垂直安装光伏组件的年发电量比地面最佳倾角安装光伏组件的年发电量低，且随着光伏组件安装地区纬度的降低，二者的发电量差值逐渐增大；

2)量化不同气候区立面垂直安装光伏组件的年发电量与地面最佳倾角安装光伏组件的年发电量的相对偏差，得到2020年哈尔滨市、北京市、上海市、广州市不同安装方式下光伏组件年发电量的相对偏差分别为21%、26%、36%、40%，低纬度地区的相对偏差较大；

3)其他气候区也可采用本文提出的公式及相对偏差来量化立面垂直安装光伏组件的发电量和地面最佳倾角安装光伏组件的发电量差异，研究结果对指导光伏发电系统设计意义重大。