遗传算法求解带时间窗的车辆路径问题

文/周景欣

引言

随着互联网的进步，电子商务业的飞速发展，人们的生活愈发信息化，车辆路径问题的客户已经从以前的大型超市、生产基地等更多的落地到如家庭、个人等小而精的客户身上。带时间窗的车辆路径问题（VRPTW）更加贴切现在和未来对于车辆路径问题的描述。VRPTW 是VRP问题的一种常见的变体，配送车辆容量有限，每一个客户都拥有一个特定的交付时间窗口所限定，车队运输需要在客户的时间窗内抵达客户所在位置为客户服务，否则将受到一定的惩罚。VRPTW 也被认为是NP-hard[1]，精确算法求解车辆路径问题仅仅适用于规模较小的问题，而面对现实世界中大型的VRPTW 时，启发式和元启发式通常更加适合[2]。模拟退火（SA）、禁忌搜索（TS）[6]、蚁群优化(ACO)[4]、遗传算法(GA)[3]、粒子群优化（PSO）[5]等算法已被证明可有效解决复杂的多目标问题，在求解车辆路径问题上取得了显著的成果。本文以最小化物流配送成本为目标，研究带时间窗的车辆路径问题，建立数学模型;为克服遗传算法收敛速度慢的缺陷，设计并采用了自适应大邻域算法中的破坏算子，通过局部搜索策略，保留较优解。通过实际算例测试表明，改进的遗传算法较简单遗传算法有较好的局部寻优能力，验证了本文算法的有效性。

1.问题描述

VRPTW 可描述为：对一系列的装货点和（或）卸货点，组织合理的行车线路，使车有序地通过它们，在满足货物的需求量、车辆的容量限制、车辆的行驶时间、顾客要求的服务时间窗口等约束条件下，以最低的总成本满足所有客户的需求[9]。时间窗可分为硬时间窗和软时间窗，本文的研究都是以软时间窗为基础。

图1-1中线路上的数值表示的是车辆的行驶时间，且以配送中心时间窗开始时间为车辆的出发时间。图1-1(a)表示配送网络优化前，配送中心服务客户的配送线路存在着大量交错运输和长距离运输的情况，并且存在违反时间窗的客户点较多，而配送网络优化后（见图1-1(b)），客户被分配到临近的配送中心接受物流服务，不仅没有出现违反时间窗的客户点，而且消除了长距离的交错运输。

图1 -1配送网络优化前后对比

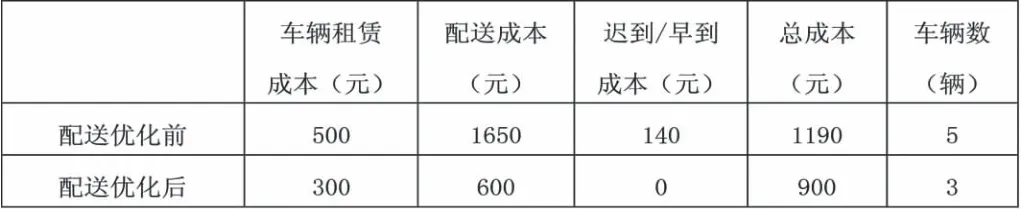
表1 -1 配送网络优化前后成本对比

2.模型建立

2.1 符号定义

配送网络优化问题的变量定义如表2-1所示。

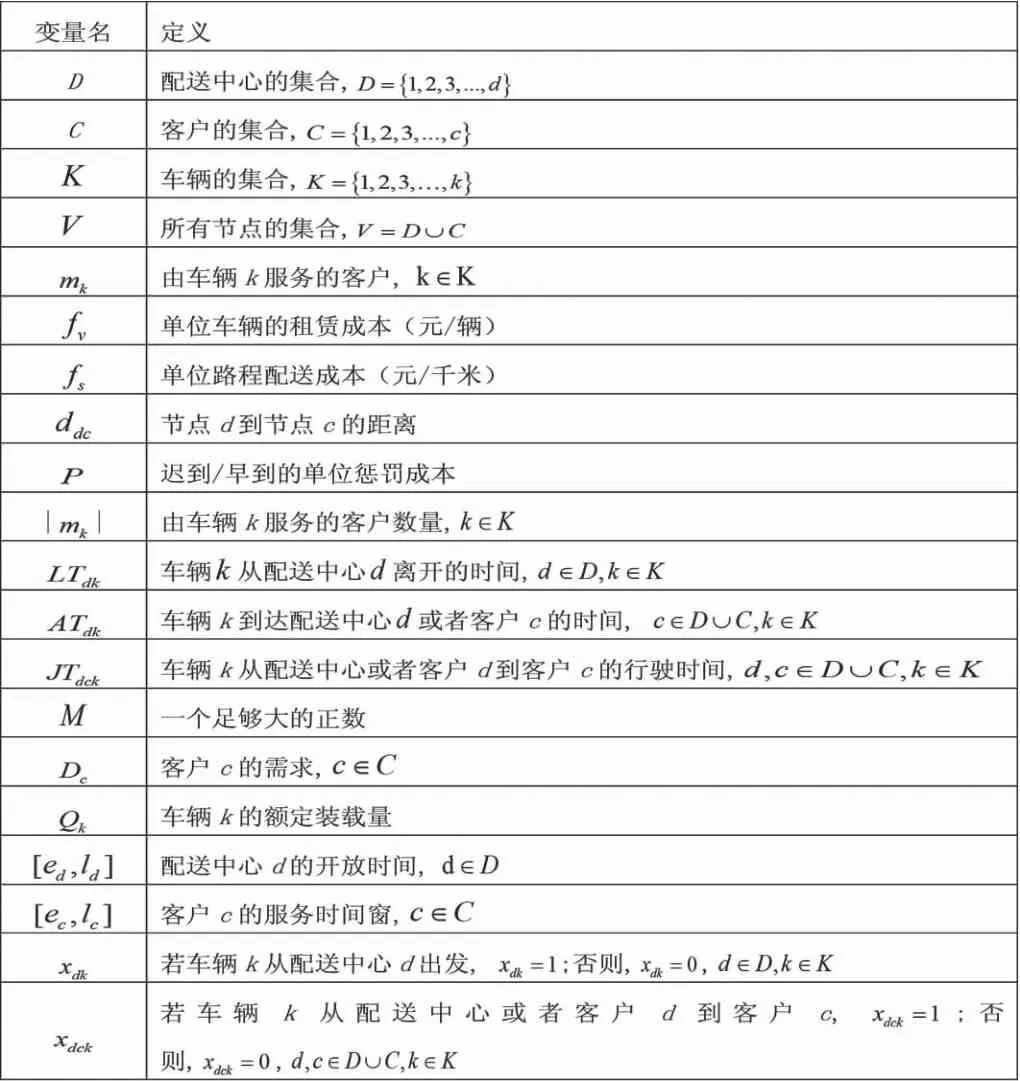
表2 -1变量定义

2.2 模型构建，为构建模型做如下假设：（1）客户的货物需求量均小于车辆的载容量，一辆车可以满足多个客户需求；（2）所有的客户均由一个配送中心供货；（3）只有一种型号的车辆参与配送；（4）车辆的行驶速度是保持恒定的，即匀速行驶、以配送物流运营成本Z最小化为目标，建立带时间窗的车辆路径优化模型:

Z3：表示配送车辆违反客户时间窗的惩罚成本。

式（5）表示一个客户仅由一辆车服务；式（6）表示每个客户仅接受一条配送线路服务；式（7）表示车辆服务客户后必须离开；式（8）表示消除线路上的子回路；式（9）表示车辆离开配送中心的时间必须在其开放时间之内；式（10）表示车辆到达配送中心的时间必须在其开放时间之内；式（11）-（14）表示时间连续性约束；式（15）表示车辆的装载量不超过车辆容量；式（16）-（17）表示决策变量。

3.改进的遗传算法

应用改进的遗传算法进行优化计算和模型求解，相关变量定义为：popsize表示种群规模，genmax表示最大迭代次数，ps，pc和pm分别表示选择，交叉和变异概率，Pt与Qt分别表示初始种群和子代种群，gen表示当前算法迭代次数。混合算法的具体流程下：Step 2：应用改进的方式生成初始种群Pt，设置gen=1。Step 3：对初始种群Pt中的染色体进行选择，交叉和变异操作生成子代种群Qt。具体的选择，交叉和变异过程如下述Step3.1-Step3.3所示[8][9][10]。Step 3.1：设计适应度函数并计算适应度函数值，根据染色体的适应度大小应用轮盘赌方法经过多轮选择确定子代种群。Step 3.2：交叉操作，根据交叉概率随机选择染色体进行交叉运算，并采用单点交叉法，两点交叉法和部分映射交叉法生成子代染色体，并与父代染色体进行比较选择子代染色体。Step 3.3：变异操作，根据变异概率随机选择染色体进行变异运算，并采用部分映射变异和互换操作算子生成子代染色体，并与父代染色体比较选择子代染色体。Step 4：将Pt与Qt合并形成新的种群Rt，评价种群个体的目标函数值。Step 5：令gen=gen+1，重复混合算法Step3进行循环操作，直到达到最大迭代次数genmax。Step 7：通过计算染色体对应个体目标函数值的大小，选取并输出最优解，结束算法。

4.算例及结果分析

4.1 算例相关数据。本文以重庆市某物流企业的配送网络为例进行研究，选择了一个配送中心和50个客户，最多可使用车辆15辆。其中配送中心的坐标为（40，50），客户点特征如表4-1所示。根据已有相关文献和实例数据规模，设置相应参数为：种群大小=100，迭代次数=100，交叉概率=0.9，变异概率=0.05。

表4 -2 优化结果

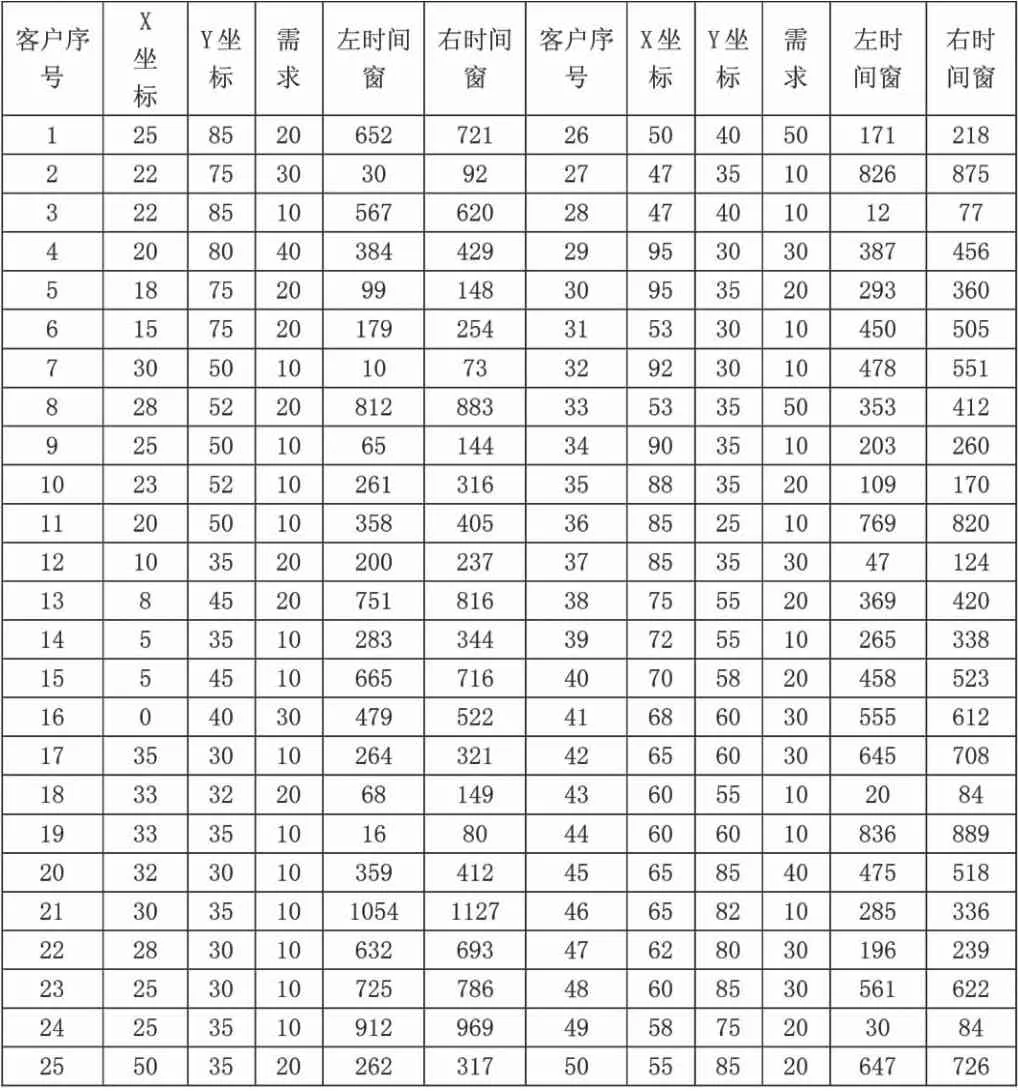
表4 -1客户特征

4.2 VRPTW 配送优化方案

在配送中心的服务周期内，应用上述改进的遗传算法求解带VRPTW 的物流成本和车辆使用数，得到8条车辆优化路径，如下所示：配送路线1：0→2→5→6→4→3→1→0；配送路线2：0→7→9→10→11→8→0；配送路线3：0→37→35→34→30→29→32→36→0；配送路线4：0→12→14→16→15→13→0；配送路线5：0→28→26→25→33→31→27→0；配送路线6：0→19→18→17→20→22→23→24→21→0；配送路线7：0→43→39→38→40→41→42→44→0；配送路线8：0→49→47→46→45→48→50→0；该结果中车辆行驶总距离为626.2806，总成本为3314.03元。

4.3 优化结果分析。由图4-2可知，车辆固定成本，惩罚成本和配送成本都有所下降，且物流运营总成本由7835.43元下降到了4114.03，直接下降了47.5%。此外，利用改进的遗传算法求解的优化结果有效地消除了违反客户时间窗的现象，并且大幅度地减少了行驶路程，从而得到了较优的结果。

结束语

本文结合配送中心对配送路径的要求，以VRPTW 为研究对象，站在物流企业的角度，建立了成本最小化的数学模型。针对遗传算法局部搜索能力差的缺点，结合混合遗传算法的特点，在标准遗传算法的基础上，改进了初始种群的生成方式，并且引进自适应大领域算法中破坏算子的移除和插入操作对个体进行局部搜索。研究结果表明，该算法对求解带时间窗约束车辆路径问题是有效的，并且能有效降低物流成本和提高配送车辆使用效率。

引用出处

[1]胡大伟,陈希琼,高扬.定位-路径问题综述[J].交通运输工程学报,2018,18(01):111-129.

[2]贺协腾.选址路径问题及其优化算法综述[J].中国新技术新产品,2009(18):13.

[3]慕晶晶.基于遗传算法的服装退货回收车辆路径优化问题研究[J].物流工程与管理,2021,43(03):123-125.

[4]熊沂铖,王栋.基于蚁群算法的车辆路径问题研究[J].信息技术,2019,43(07):15-17+23.

[5]胡小宇,刘庆,贺文宁,马炫.基于粒子群算法的单仓储多车物流配送优化[J].计算机应用,2018,38(S2):21-26.

[6]李阳,范厚明,张晓楠,杨翔.求解模糊需求车辆路径问题的两阶段变邻域禁忌搜索算法[J].系统工程理论与实践,2018,38(02):522-531.