基于ANSYS Workbench/Ls-Dyna的锤片—菌草粉碎系统的功耗模型分析

万家明, 陈伟祥, 陈重成, 郑书河

(福建农林大学机电工程学院/现代农业装备福建省高校工程研究中心，福建 福州 350002)

为了解决我国食用菌产业高速发展带来的“菌林矛盾”，我国学者林占熺于1983年从非洲引入巨菌草在国内种植[1].菌草具有对生长环境要求不高、生长周期短、产量高、营养成分高等特点，很快被推广种植[2-3].菌草在生态环境建设、畜牧业发展、能源开发以及材料研发等方面都具有很好的应用前景[4-8].

由于菌草的生产规模不断扩大，对菌草加工处理环节的要求也不断提高.现阶段用于秸秆粉碎的设备主要有锤片式粉碎机、铡草机、揉搓机等，其中锤片式粉碎机由于操作方便、结构简单、通用性好等特点被广泛应用[9].但目前锤片式粉碎机仍然存在粉碎效率低、耗能高的问题.田海清等[10]为了提高粉碎机的粉碎性能，设计了一种由圆弧、等边角、翼形弧组成的筛网，结果表明在相同条件下，该筛网对物料的粉碎效果比普通环形筛网好；王德福等[11]利用高速摄像仪对玉米秸秆的粉碎过程进行观察，发现其主要的粉碎形式为击打粉碎、撞击粉碎和搓擦粉碎，并通过试验分析了含水率、转速、筛网直径对度电产量的影响；Michaela et al[12]研究了锤片线速度、空气流量、筛网直径对粉碎机产量以及粉碎效果的影响，研究表明，锤片的线速度与筛网直径对于物料粉碎后的平均粒径有显著影响，而空气流量对平均粒径的影响不显著；苏从毅等[13]对锤片的结构进行了研究，设计了一种开刃锤片，物料与该锤片撞击后的周向线速度比传统矩形锤片降低了30%～50%，从而降低物料与锤片的速度差，增大碰撞力，提高粉碎效果；Bochat et al[14]设计了一种新型三角锤片，该锤片可以破坏锤片式粉碎机内的环流层，与传统的矩形锤片相比，这种锤片的撞击面积更大，且本身具有的倾斜角度可以增大物料的径向速度，使得物料更容易通过筛网.

目前大多数研究主要针对粉碎机整体工作性能的提升，对于锤片与物料的碰撞粉碎过程未作深入研究.本研究以锤片式粉碎机为基础，设计了一种新型锤片；并以该锤片为研究对象，对锤片—菌草粉碎系统的碰撞、粉碎过程进行研究，探究在不同作业参数下锤片与菌草碰撞时的碰撞力、功率的变化趋势，以及影响碰撞力及功率的参数，旨在提高粉碎机的粉碎效率，降低粉碎功耗.

1 材料与方法

1.1 锤片—菌草粉碎系统力学模型的建立

图1 碰撞的几何模型Fig.1 Geometric model of impact

锤片式粉碎机的工作原理是通过锤片对物料进行反复击打，同时利用物料与筛网、物料与物料之间的摩擦、碰撞来粉碎物料.图1为锤片与菌草茎秆的碰撞几何模型示意图.从图1可知，工作时，锤架板转动使得销轴带动锤片转动，锤片获得动能后与菌草茎秆发生碰撞，从而打断、粉碎菌草.

根据矩形锤片以及菌草茎秆的特点，并参考文献[15]设计了新型锤片，如图2所示.通过将锤片击打的端面设计成斜面并对两侧材料进行一定的去除，提高锤片与物料的接触时间，增大物料受到的击打力，使得物料被粉碎得更加充分，提高材料的利用效率；同时由于增大了击打端面的厚度，锤片末端的质量更大，其对物料击打的动能也更大，且末端的倾角与物料发生碰撞时更容易击碎物料，有利于提高粉碎效率.

新旧锤片碰撞的受力分析如图3所示.

根据几何关系可知：

(1)

(2)

则撞击点B、C的线速度分别为：

vB=ωr2

(3)

vC=ωr3

(4)

根据动量定理可知：

Ft=mv1-mv2

(5)

设新旧锤片的撞击时间均为t，质量为m，则新旧锤片的碰撞力分别表示如下：

(6)

(7)

两者碰撞力之差为：

(8)

图2 锤片结构Fig.2 Hammer structure

1.2 锤片—菌草粉碎系统仿真模型的建立

通过三维建模软件SolidWorks对锤片—菌草粉碎系统的碰撞模型进行建模.菌草的结构分为3层，分别为最外层的韧皮部、中间层的木质部以及最内层的芯部.其中最内层的芯部为髓腔结构，韧皮部和木质部对于茎秆的强度起主要贡献作用，而髓腔的强度很小，因此可将菌草茎秆简化为薄壁空心圆柱模型[16]；同时为了方便计算，对这一结构进行简化，将锤片与锤架板设置为固定连接.建模完成后将建立的几何模型以Parasolid(*.x_t)文件格式进行保存，并导入ANSYS Workbench/Ls-Dyna模块中.

利用材料库对锤片以及菌草茎秆的材料进行设置，锤片材料采用结构钢，因为锤片在碰撞过程中变形极小，故将其设置为刚体；由于菌草是一种非线性、各项异性的弹性材料[17]，因此采用弹性正交各项异性材料模型(*MAT_ORTHOTROPIC_ ELASTIC)对菌草茎秆的材料属性进行设置.菌草茎秆的材料参数[18]如表1所示.

表1 菌草茎秆的材料参数Table 1 Mechanical parameters of JUNCAO stem

模型网格的划分是进行有限元分析和求解的重要环节，网格的类型和粗细不但影响计算结果的准确性，同时对计算机的计算效率也有影响.网格划分得越细，其求解精度越高，计算结果越准确.但是过密的网格会增大计算机的工作负担，延长求解时间，降低求解效率，因此对菌草茎秆与锤片发生碰撞的部位进行网格加密处理，其余部分采用自动网格划分；同时对菌草茎秆的网格结构进行面映射，形成更加均匀的六面体网格.由于锤片是刚体，网格的质量对仿真结果影响不大，故采用自动网格方法进行划分，网格划分结果如图4所示.

对模型进行网格划分后再对其进行初始条件的设定，由于锤片是通过绕中心旋转来对菌草进行击打，除了保留绕z轴转动的自由度，对其他5个自由度进行约束.为了模拟真实情况下菌草被击打的过程，对菌草茎秆不施加约束，使其具有6个方向的自由度，并设定仿真时间，添加侵蚀接触，以保证仿真的准确性.

1.3 单因素与多因素试验的设计

为了研究锤片转速、锤片斜面倾角、菌草茎秆直径对碰撞粉碎功耗的影响，以转速、斜面倾角、茎秆直径3个因素为变量，以最大碰撞力和平均功率为试验指标，对锤片—菌草粉碎系统的碰撞过程进行单因素试验的动力学仿真，分析转速、斜面倾角、茎秆直径对最大碰撞力以及平均功率的影响程度.对转速、斜面倾角、茎秆直径选取5个水平进行碰撞仿真试验，因素水平如表2所示.

表2 因素水平表Table 2 Factors and levels

表3 因素水平编码表Table 3 Coding of factors and levels

为了进一步研究转速、斜面倾角、茎秆直径之间的相互影响及其对碰撞力和功率的影响，确定最佳的参数，减少碰撞粉碎过程中的功耗，在单因素试验的基础上进行多因素试验.采用响应曲面Box-Behnken试验方案，以最大碰撞力和平均功率为指标，对转速、斜面倾角、茎秆直径进行三水平三因素试验.根据单因素分析中确定的因素取值范围进行因素水平的选择，其因素水平如表3所示.

图4 网格划分Fig.4 Grid partition

2 结果与分析

2.1 碰撞过程

对模型进行求解，将求解后的d3plot文件导入Ls-Prepost结果处理软件中查看仿真结果.从图5可看出，锤片与茎秆碰撞时部分茎秆会被锤片击打飞出、断裂，而茎秆未出现明显的变形.根据文献[18]，茎秆破坏前可分为2个阶段：第1个阶段近似弹性阶段，此时茎秆的应力与应变呈线性关系，虽然发生弹性变形，但其变形量很小；第2个阶段中当茎秆受到的应力大于极限应力，茎秆发生断裂.未发生明显变形的一个原因是茎秆与锤片碰撞时，受到的应力超过其自身能够承受的极限应力，另一个原因可能是未对茎秆的自由度进行约束使得变形量不明显.

从图6、7可以看出：菌草茎秆在约0.15 ms内与锤片发生碰撞，最大碰撞力为77 N；随着碰撞时间的变化，锤片动能逐渐减小，而碰撞时产生的振动使得碰撞力以脉冲的形式出现，但是在各阶段峰值时碰撞力的大小呈先减小后增大的变化趋势.锤片与茎秆刚开始接触时，两者的相对速度大，所以碰撞力也大；随着碰撞的不断发生，锤片在经过中间的空心区域时，由于碰撞面积和相对速度减小，其受到的阻力也减小；当锤片穿过茎秆中间的空心区域到达茎秆内壁时，接触面积增大，导致受到的阻力也增大；当锤片逐渐穿过内壁时，接触面积减小，受力也减小；2.37 ms后其动能不再变化，碰撞力也变为0，此时碰撞结束.整个碰撞过程总耗时2.37 ms，锤片动能损耗418 mJ，平均功率182 W.

图5 菌草的断裂过程Fig.5 Breaking process of JUNCAO

图6 锤片—锤架板的动能变化Fig.6 Kinetic dynamics of hammer and stand

2.2 单因素试验

图8 不同转速下的最大碰撞力与平均功率Fig.8 Maximum impact force and average power at different rotational speeds

从图8可知，最大碰撞力随着转速的增大呈现先下降后升高再下降的变化趋势，最大碰撞力出现在2 200 r·min-1处，为103 N；最小碰撞力出现在3 100 r·min-1处，为43.54 N.平均功率则随着转速的增大，呈逐渐上升的趋势，最大值出现在3 400 r·min-1处，为228.57 W；最小值出现在2 200 r·min-1处，为121.43 W.从图9可知，随着斜面倾角的增大，最大碰撞力呈先减小后增大的趋势，最小值出现在10°倾角，为77 N；最大值出现在5°倾角，为106 N.平均功率随着倾角的增大呈现先减小后增大的变化趋势，最大值出现在10°倾角，为179.4 W；最小值出现在7.5°倾角，为149 W.由图10可知，最大碰撞力随着菌草直径的增大呈先下降后增大的变化趋势，最大值出现在22 mm，为88.7 N；最小值出现在20 mm，为77 N.平均功率随着菌草直径的增大呈增大的趋势，最大值出现在24 mm，为191.58 W；最小值出现在16 mm，为140.24 W.

根据单因素试验结果，以最大碰撞力和最小碰撞功率为标准，确定各影响因素的取值范围：锤片转速2 500～3 100 r·min-1，锤片斜面倾角5°～10°，菌草茎秆直径18～22 mm.

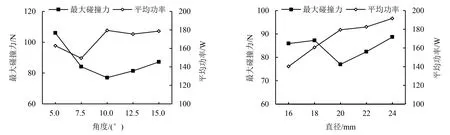
图9 不同斜面倾角下的最大碰撞力与平均功率Fig.9 Maximum impact force and average power at different inclined angles

2.3 多因素试验

多因素试验结果如表4所示.

表4 多因素试验结果1)Table 4 Results of multi-factor test

利用软件Design-Expert对碰撞仿真数据进行拟合，建立最大碰撞力、平均功率的二次多项式回归模型.

Y1=-399.289 72+1.244 63A-52.722 17B-92.185C+0.006 637AB-0.009 925AC+1.155BC-0.000 206A2+0.400 6B2+2.680 31C2

(9)

Y2=-150.280 63+0.075 762A-39.413 14B+16.446 05C+0.002 085AB-0.027 11AC-0.036 45BC+0.000 096A2+2.304 44B2+1.633 01C2

(10)

由表5、6可知，最大碰撞力的回归模型和平均功率模型的P值均小于0.000 1;失拟项的P值大于0.05，说明最大碰撞力、平均功率的回归模型与实际情况的拟合程度较高.由各因素的P值可知：3个因素对最大碰撞力均有极显著影响，且各因素之间的交互作用对模型有极显著影响，对最大碰撞力的影响程度从大到小依次为转速、斜面倾角、茎秆直径；转速和茎秆直径对平均功率有极显著影响，斜面倾角对于平均功率有显著影响，影响程度从大到小依次为转速、茎秆直径、斜面倾角.同时，转速与斜面倾角的交互作用显著，转速与茎秆直径的交互作用极显著，斜面倾角与茎秆直径的交互作用对模型的影响不显著.

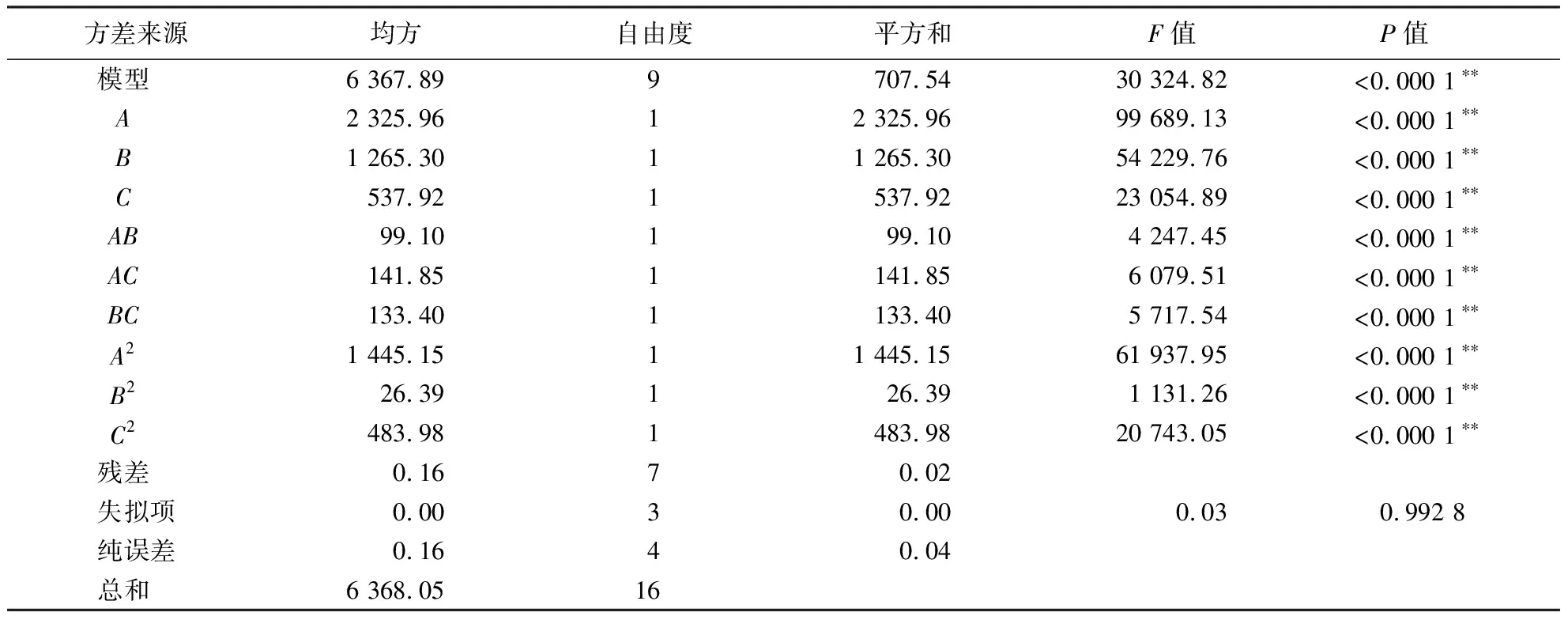
表5 最大碰撞力的方差分析1)Table 5 ANOVA of maximum impact force

根据拟合的二次回归模型，通过Origin软件绘制各因素交互的3D响应曲面图(图11、12).由图11可知：当斜面倾角保持不变时，最大碰撞力随转速的增大呈先小幅增大后减小的变化趋势；当转速保持不变时，最大碰撞力随斜面倾角的增大而增大.由图11可知：当转速保持不变时，最大碰撞力随茎秆直径呈先减小后增大的变化趋势；当茎秆直径保持不变时，随着转速的增大，最大碰撞力呈先增大后减小的变化趋势.由图11可知：当斜面倾角保持不变时，随着茎秆直径的增大，最大碰撞力逐渐减小；当茎秆直径保持不变，最大碰撞力随斜面倾角的增大呈逐渐减小的变化趋势.

由图12可知：当斜面倾角保持不变，平均功率随着转速的增大而增大；当转速保持不变，平均功率随着斜面倾角的增大呈先减小后增大的变化趋势.根据图12可知：当保持在低转速时，平均功率随着茎秆直径的增大而增加；在靠近3 100 r·min-1处，平均功率随着茎秆直径的增大呈小幅增大的变化趋势；而茎秆直径保持不变时，平均功率随着转速的增大而增大.由图12可知：当斜面倾角保持不变时，平均功率随茎秆直径的增大而增大；当茎秆直径保持不变时，平均功率随斜面倾角的增大呈先减小后增大的变化趋势.

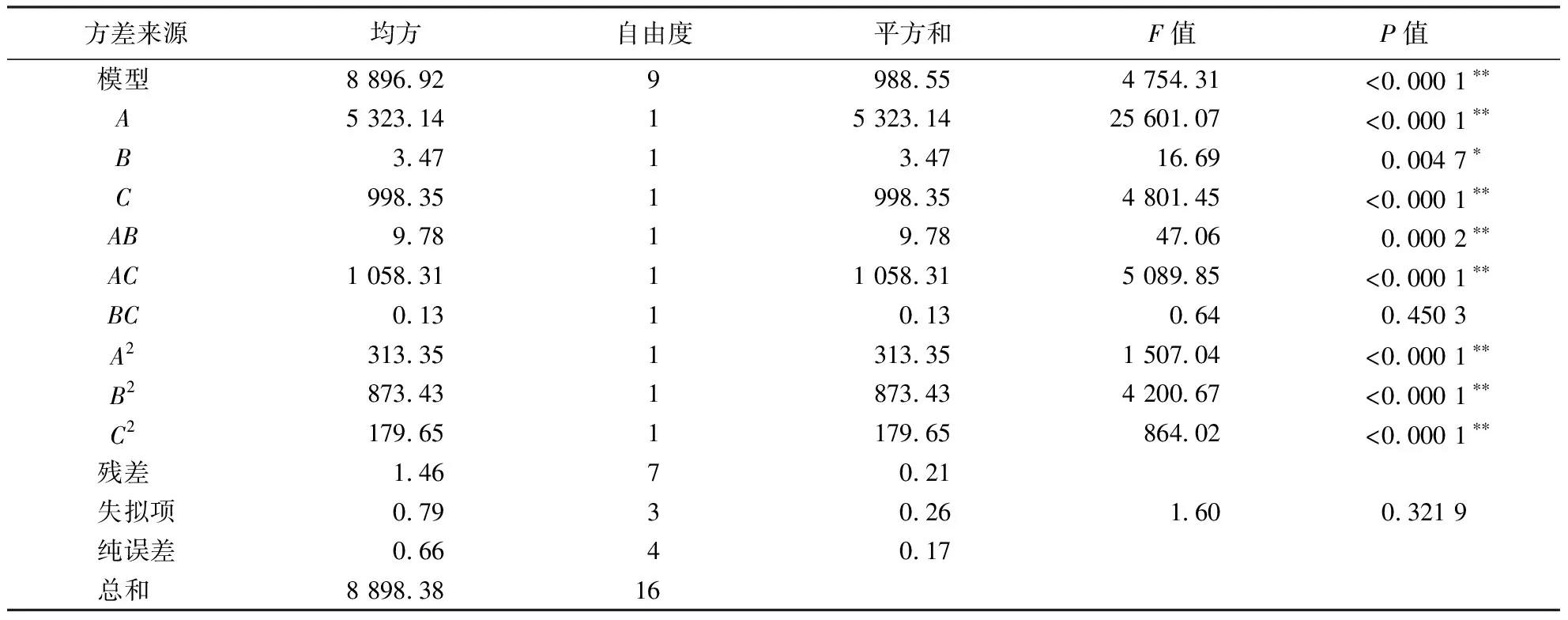
表6 平均功率的方差分析1)Table 6 ANOVA of average power

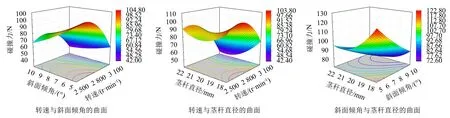
图11 两因素对最大碰撞力的响应曲面Fig.11 Response surface modelling of effect of 2 factors on maximum impact force

通过Design-Expert对结构参数进行优化，在茎秆直径取最大值(22 mm)的条件下，以最小平均功率为主要优化目标，以最大碰撞力为次要优化目标，求解最佳参数组合.最佳优化结果为：转速2 623.18 r·min-1，斜面倾角7.12°，最大碰撞力95.37 N，平均功率165.15 W.将优化后的参数作为试验条件，对碰撞模型进行仿真，仿真后的最大碰撞力为105 N，与模型的误差为10%；平均功率为163.14 W，与模型的误差为1.22%，两者与优化所得的预测值都较为接近.

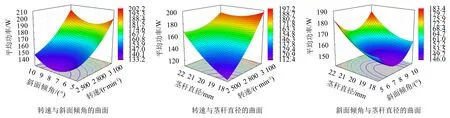
图12 两因素对平均功率的响应曲面Fig.12 Response surface modelling of effect of 2 factors on average power

3 小结

本研究基于锤片式粉碎机，根据锤片的工作特性对锤片进行了优化设计，并建立新旧锤片与菌草碰撞的力学模型，对碰撞过程进行了分析；利用ANSYS Workbench/Ls-Dyna对锤片—菌草粉碎系统的碰撞过程进行动态仿真分析，并得到碰撞过程中的碰撞力和动能变化曲线；以转速、斜面倾角、茎秆直径为影响因素，以最大碰撞力和平均功率为指标进行单因素试验，确定影响因素的取值范围；通过Design-Expert软件设计了三因素三水平的响应曲面试验，对试验结果进行了方差分析，结果表明对最大碰撞力的影响程度表现为：转速>斜面倾角>茎秆直径.对平均功率的影响程度表现为：转速>茎秆直径>斜面倾角.建立最大碰撞力和平均功率的回归模型，得到茎秆直径为22 mm时的最佳参数：转速2 623.18 r·min-1，斜面倾角7.12°，在此参数下，最大碰撞力95.37 N，平均功率165.15 W.根据得到的最佳参数进行仿真试验，验证优化结果的可靠性，结果表明最大碰撞力与模型的误差为10%，平均功率与模型的误差为1.22%，与预测结果较为接近，表明模型可靠性较高.