基于模糊聚类和动态K值的室内定位算法

董世鹏，吴韶波

（北京信息科技大学 信息与通信学院，北京 100101）

0 引 言

基于WiFi的指纹定位由于具有低成本、易部署、非视距等优点，已成为室内定位领域研究的热点[1]。目前典型的WiFi指纹匹配算法是K近邻（KNearest Neighbor, KNN）算法及其改进算法，通过比较待测点与指纹库中参考点指纹强度距离，推算出待测点位置。但在室内环境中受多径及障碍物遮挡等因素影响，WiFi信号强度存在波动，导致单纯基于信号强度的定位算法将错误参考点归入近邻点中，增加定位误差[2]。

文献[3]在离线阶段根据参考点空间位置进行聚类，在线匹配时在同一类簇参考点中选择近邻点，避免将偏离空间中心的参考点加入到近邻点，但离线阶段和在线阶段聚类标准的不同无法保证在线聚类匹配的准确性。文献[4]采用改进的组合加权指纹定位算法，剔除偏离几何中心的近邻点，将满足条件的近邻点结合实际位置与欧氏距离进行加权，没有考虑不同欧氏距离下近邻点定位可靠性，使估算出的几何中心与测试点实际位置的距离较远。

由于基于K近邻的定位算法需要计算测试点与指纹库中所有参考点的距离，当指纹库中参考点数量过多时，难以保证定位实时性。因此，通常需要对指纹进行聚类，减少在线定位阶段需要计算的参考指纹数量，提高定位效率。文献[5]中提出基于FCM聚类及KNN算法的指纹定位方法，文献[6]中提出一种基于亲和力传播聚类的定位方法，文献[7]利用层次聚类对指纹库进行划分，均有效地降低了计算复杂度。但以上方法都没有考虑到聚类边缘处参考点选取问题。文献[8]在二分K-means聚类的基础上，根据聚类中心与样本点欧氏距离阈值选择类簇，将满足条件类簇的所有指纹数据添加到参考点中，提高聚类边缘处定位精度，但会引入过多指纹。文献[9]中对数据在不同聚类的隶属度差值进行划分，但不适合样本位于多个聚类边缘处的情况。

针对以上问题，本文提出了一种结合改进FCM聚类与动态K值定位的改进算法。离线阶段在传统FCM聚类的基础上，将隶属度大于阈值的参考指纹添加到对应类中，降低聚类边缘处指纹数据不足引起的误差。结合指纹强度信息与近邻点空间位置，剔除距离预测中心点较远的近邻点，并根据WKNN算法得出定位结果。

1 WiFi指纹定位算法

WiFi指纹定位可以分为离线指纹库构建和在线定位两个阶段。离线指纹库构建阶段，采集并保存在各参考点采集到的指纹信息；在线定位阶段，根据离线指纹库及测试点采集到的指纹信息推算测试点位置。

1.1 离线指纹库构建

在待定位区域按照一定间隔设置参考点，并建立相应坐标系。记录每一个参考点处采集到的指纹信息强度及对应坐标，并保存到指纹库FP中，如下式：

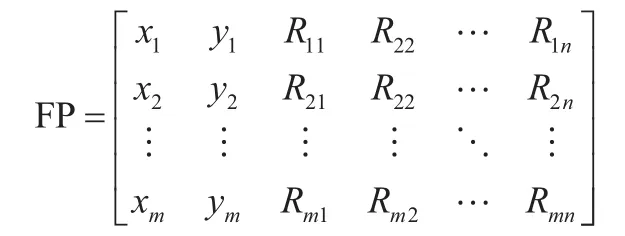
其中：（xi,yi）表示第i个参考点的坐标；Rij表示在第i个参考点接收到的第j个AP的指纹强度。

1.2 在线定位匹配

由于KNN算法[10]及WKNN算法[11]都是选取固定K个近邻点，在判定近邻点时容易引入信号距离较远的点，导致定位精度降低。EWKNN算法[12]通过设定指纹强度距离阈值确定定位时的近邻点及K值，有效避免了相似度较小近邻点的引入，提高了定位精度。故在线定位阶段本文选择在传统EWKNN算法的基础上进行改进，通过结合指纹强度距离与空间距离对近邻点进行二次筛选，进一步提高定位精度。

2 FCM聚类算法及改进

2.1 FCM算法原理

FCM聚类算法是一种模糊理论与HCM算法结合的软聚类算法，使用[0，1]之间的隶属度来表示数据属于某个类的概率，并且样本对于所有类簇的隶属度之和为1。样本在类簇中具有越高隶属度，则属于该类的可能越大，并将隶属度最高的类作为样本所属聚类[13]。

FCM算法中代价函数定义为：

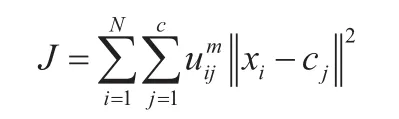
其中：J为代价函数；N为数据个数；c为聚类个数；uij为第i个数据对于第j个聚类的隶属度；m为权重系数；||xi-cj||2为数据xi到聚类中心cj的距离。

通过拉格朗日公式对代价函数求导，最终可以得到聚类中心点和隶属度的迭代公式分别为：

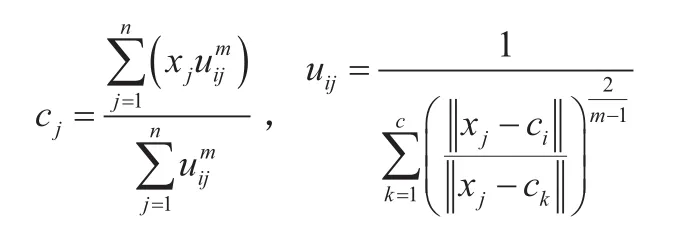
2.2 FCM算法步骤

FCM聚类算法的基本流程如图1所示。

离子液体是由离子组成的有机盐化合物，在室温下多为流动状态的液体，对纤维素等聚合物具有良好的溶解性能。在纤维素向5-HMF的催化转化过程中，离子液体被广泛采用[12]。

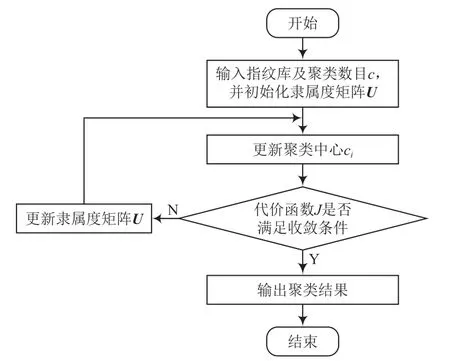
图1 FCM聚类流程

2.3 基于隶属度最小值的聚类划分

当测试样本在指纹聚类边缘处时，近邻点可能被划分到不同聚类中，使聚类边缘处的测试样本无法获得足够参考点造成定位精度降低。由于在FCM算法中聚类边缘处的样本对于相邻类别都有较高隶属度，故在FCM聚类算法中加入最小隶属度阈值对指纹数据进行划分。

在传统FCM聚类中加入最小隶属度阈值m，当样本i在该类簇中隶属度值最大或隶属度大于固定阈值m时，将样本i加入到该类中，使在多个类簇中有较高隶属度的样本可以划分到不同聚类。

3 结合模糊聚类的动态K值定位

为解决WiFi指纹定位中聚类边缘处参考点不足造成定位精度降低及部分近邻点偏离空间中心导致的定位精度下降的问题，提出了一种结合最小隶属度的FCM聚类和动态K值的定位算法。算法的整体流程如图2所示。

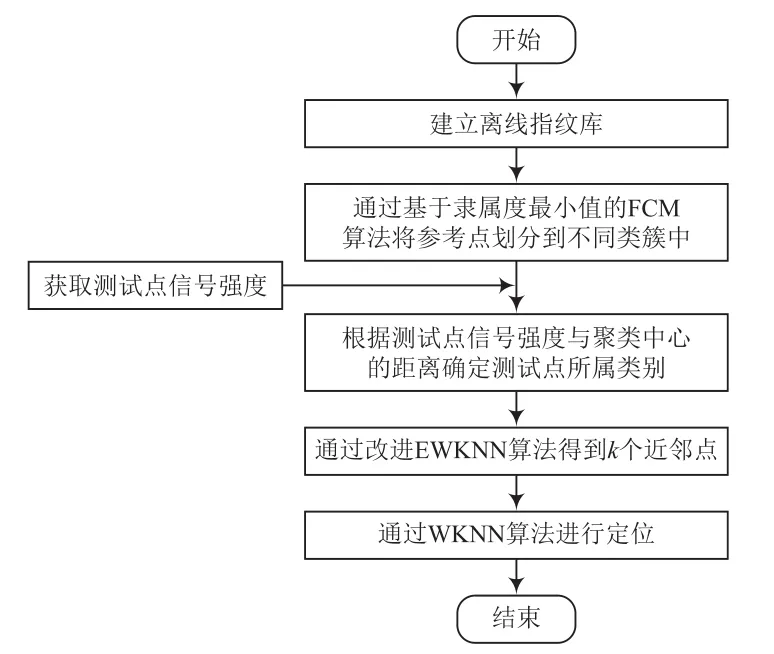
图2 改进算法流程

针对传统指纹定位算法进行在线定位时部分近邻点偏离空间中心较远导致定位精度降低问题，提出一种基于欧氏距离和近邻点之间空间距离的K值确定方法，对近邻点进行二次筛选。具体算法步骤如下：

（1）将设备从周围接入点收集到的信号强度序列与指纹数据库中的指纹序列进行计算，得到测试点信号强度与所有参考指纹序列的距离为：

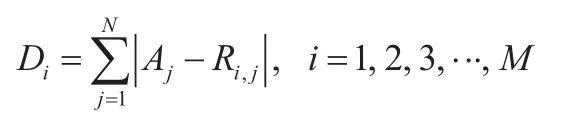
其中：Aj为第j个AP的RSSI；Ri,j为第i个参考点处第j个AP的RSSI；M为指纹库中参考点个数；N为指纹库中AP个数。

（2）将Di按照升序排列，即Di中最小值为D1，最大值为DL，设定阈值D，将序列中大于D的点筛除，得到G个参考点。用Sg表示D1和Dg之间的差（g=2, 3,...,G）。计算Sg的平均值为：

筛除Sg大于E(S)的参考点，并将剩余参考点数目设置为K，按照升序排列为[D1,D2,...,DK]，作为待筛选近邻点。

（3）定义初始中心坐标为（xcen,ycen），且有：

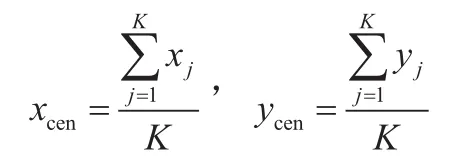
（4）计算坐标D1(x1,y1)与中心点坐标（xcen,ycen）距离，若小于阈值L则将中心坐标更新为（x1,y1），否则剔除近邻点D1并对近邻点D2进行判断。若满足阈值要求，将中心坐标更新为（x2,y2）并执行步骤（6），若不满足则执行步骤（5）。

（5）计算D1与D2坐标均值（x12,y12）与中心点坐标（xcen,ycen）距离，若小于阈值L则将中心坐标更新为（x12,y12）。

（6）计算下一个近邻点与中心坐标距离：

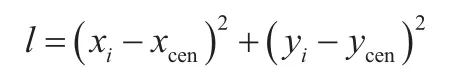
（7）若l＜L，则将近邻点Di添加到指纹序列d中，并更新中心点坐标为：

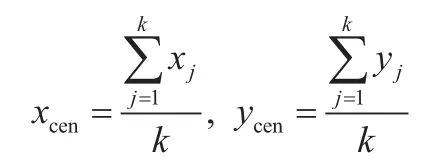
其中：k为满足阈值条件的近邻点个数；xj和yj为指纹序列d中的近邻点。

（8）重复步骤（6）和步骤（7），判断其余近邻点。

（9）对满足条件的近邻点序列[d1,d2,...,dk]，通过WKNN算法估计测试样本位置（xcen,ycen）。

4 实验结果与分析

4.1 实验环境

实验设置在学院教学楼6楼走廊进行，实验场地为50 m×2 m的长方形区域，以1 m×1 m采样间隔构建离线指纹库。使用红米Note7手机进行WiFi信号采集，并使用MATLAB2016a软件对算法有效性进行验证。实验环境如图3所示。

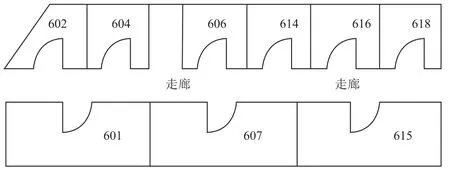
图3 实验区域平面

离线阶段：使用自主开发的WiFi信息采集APP在每个参考点处采集WiFi指纹信息，共采集100个参考点，每个参考点采集RSSI信号数据30次，将数据进行高斯均值滤波后存储到指纹数据库中。

在线阶段：在实验区域内随机选择60个测试点，每个测试点采集RSSI信号10次，将经过均值滤波处理后的数据存储为测试样本。

4.2 实验结果与分析

为验证本文提出的动态K值定位算法，分别使用基于传统FCM聚类的WKNN算法、EWKNN算法和本文提出的动态K值算法对测试点进行位置估计，其中改进定位算法阈值L设定为3，定位结果如图4及表1所示。基于传统FCM聚类的动态K值算法平均误差为1.25 m，达到累计概率80%时的误差为2.06 m，均低于EWKNN和WKNN算法，其中平均定位误差分别降低12%和24%。

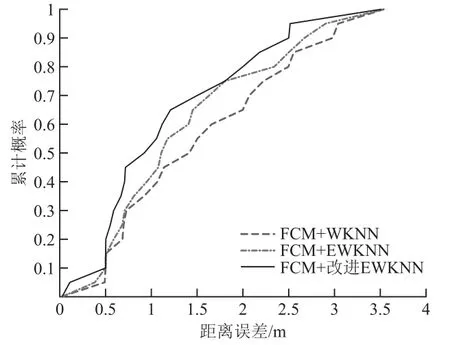
图4 三种算法定位误差

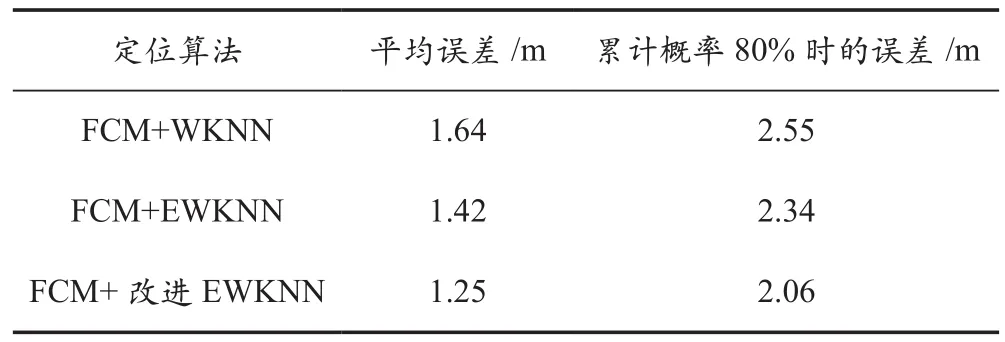
表1 三种算法定位误差对比

对于聚类边缘处缺少近邻点导致的定位精度下降问题，选取不同的m值进行多次实验，发现当m取0.1时基于最小隶属度的FCM聚类效果最好。故取隶属度最小阈值m为0.1，并对基于传统FCM的改进EWKNN算法及本文所提算法进行位置估计，实验结果如图5及表2所示。与基于传统FCM聚类的动态K值定位方法比较，本文改进算法定位平均误差及达到相同累计概率的定位误差均有所降低，分别减少了5%和3%。

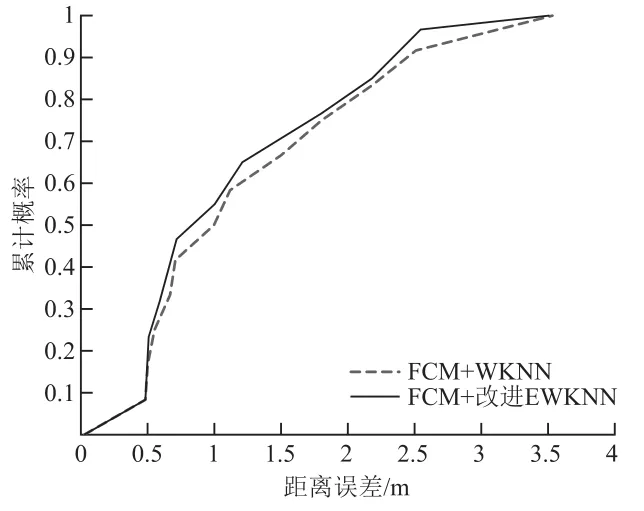
图5 聚类效果比较

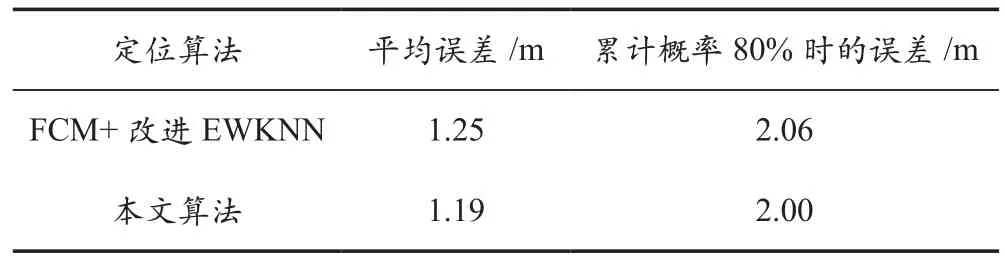
表2 聚类效果比较

将本文改进算法与基于传统FCM聚类的WKNN算法及EWKNN算法进行对比，平均定位误差分别降低27%和16%，累计概率达到80%时的定位误差分别降低26%和15%，提高了定位精度。

5 结 语

针对传统指纹定位中近邻点选择及聚类边缘处精度下降问题，本文提出了一种结合最小阈值聚类与动态K值的指纹定位算法。在离线阶段，根据最小隶属度阈值对样本进行聚类，将传统聚类边缘点处的样本点划分到多个类别中，降低聚类边缘处因缺少参考点而导致的定位误差。针对在线阶段，提出了一种结合指纹强度与参考点位置的动态加权K近邻算法，对具有较低指纹序列相似度及偏离空间中心的近邻点进行剔除，有效提高了定位精度。实验结果表明，本文提出的改进算法虽然在一定程度增加了计算复杂度，但相较传统算法定位精度有了较大提升，验证了算法的有效性。