通过关联预测对古代玻璃制品成分分析

＊殷宇龙

（哈尔滨工程大学 黑龙江 150001）

目前已有电子探针、光谱分析仪等各类高精仪器能对古代文物的成分进行定量分析。本文主要探究通过关联预测等数学方法分析古代玻璃组分的有效性。

1.模型假设

（1）假设所给的有效数据均准确，不存在错误。

（2）假设未检测出的成分在该样本中不存在。

（3）假设样本数量极少的两项与其他成分不存在相关性。

2.符号说明

符号说明：

3.模型的建立与求解

(1)问题一：模型的建立与求解

①数据的预处理。由于检测手段等多方面的原因导致部分数据中成分比例之和可能并不为100%，假设成分比例累加和介于85%～105%之间的数据为有效数据。以蜻蜓眼玻璃珠[3]为例，利用Excel将不满足范围要求的数据剔除，后续建模过程中不再重申。

②模型的建立与求解。玻璃类型、纹饰和颜色属于离散化的变量，为量化三者对表面风化的关系，建立最优标度法模型，通过SPSS对得到相关性和容差值如表1。

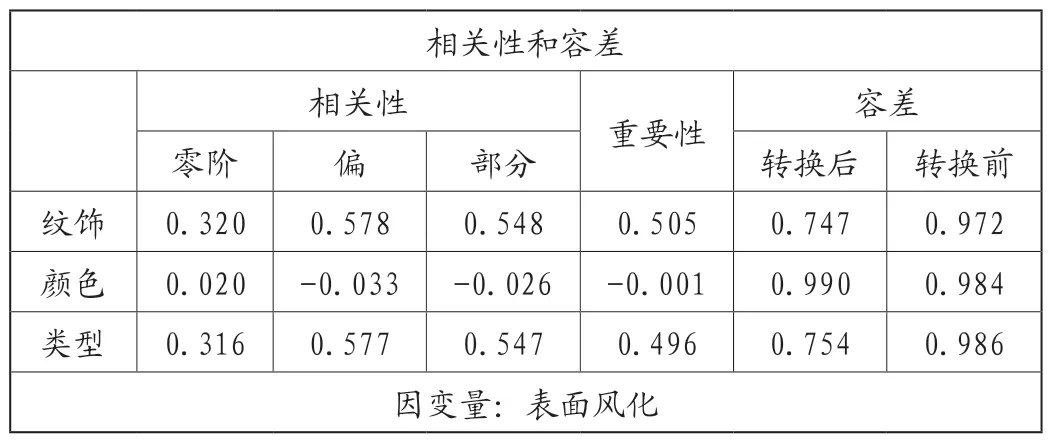
表1 玻璃类型、纹饰和颜色与表面风化的相关性和容差表

从表1中可以得到玻璃文物的纹饰和类型对表面风化具有较高的相关性，同时由于容差较大因此使得结果可信度好，进一步得到三者对表面风化的影响系数如表2。

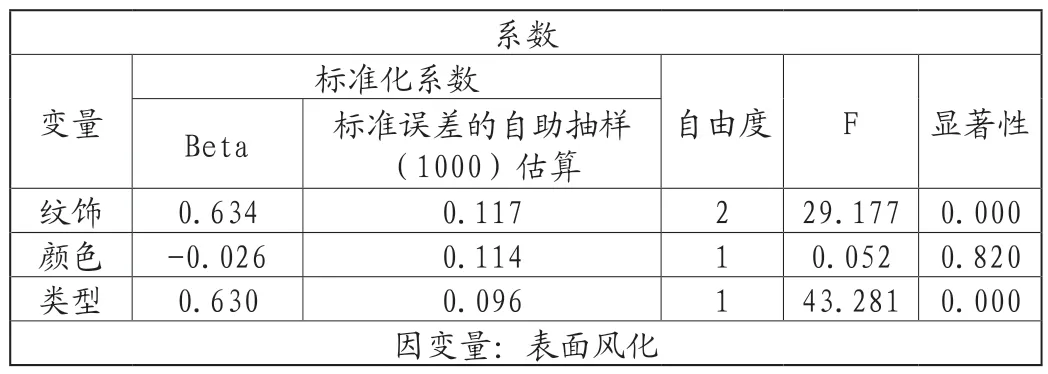
表2 玻璃类型、纹饰和颜色对表面风化影响系数

为了预测其风化前的值，依据t检验进行预测。当t＞0.05时铅钡的数据方差具有齐性的特征，便可以直接由平均值差值来求得其风化前的数值，故铅钡类风化前化学成分预测公式如下。

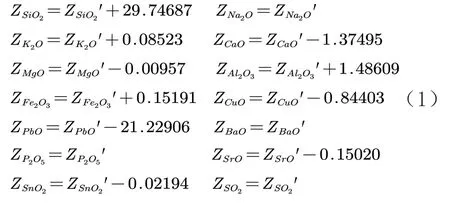
铅钡类[2]风化前化学成分预测表如表3所示。

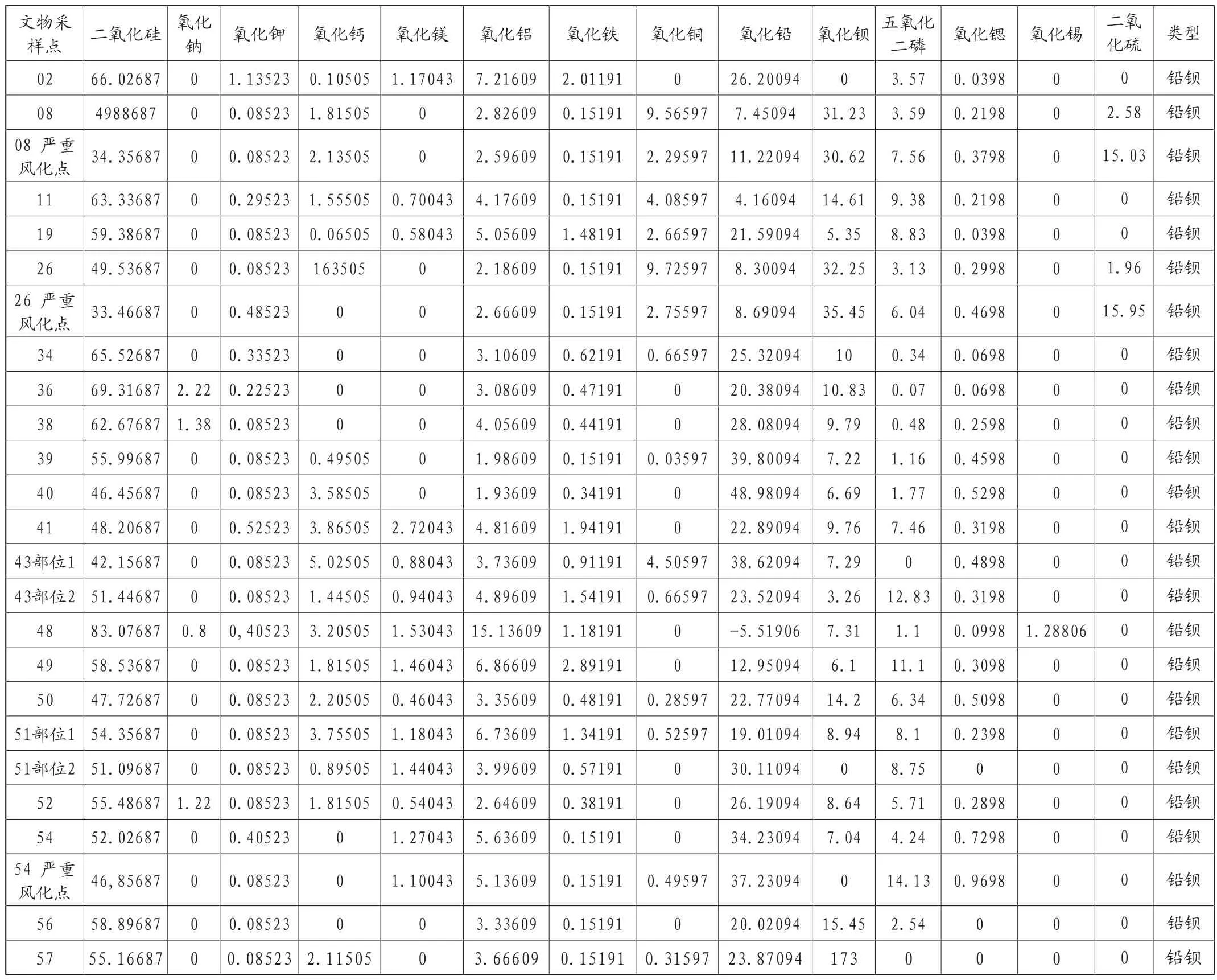
表3 铅钡类风化前化学成分预测表

而高钾的莱文方差不具有统计学意义，因此采取另一方案。

在玻璃风化过程中SiO2的净含量不变[1]，其他物质的含量会逐步减少，以致使得SiO2百分比含量上升。据此，本文利用风化过程中SiO2的含量作为刻画风化程度的变量，通过的SiO2含量，将剩余物质的百分比含量通过利用步进法做回归分析，得到六个最相关的变量。通过回归分析，得到了回归系数，为下阶段求出回归前的变量作铺垫。回归分析表格如表4所示。

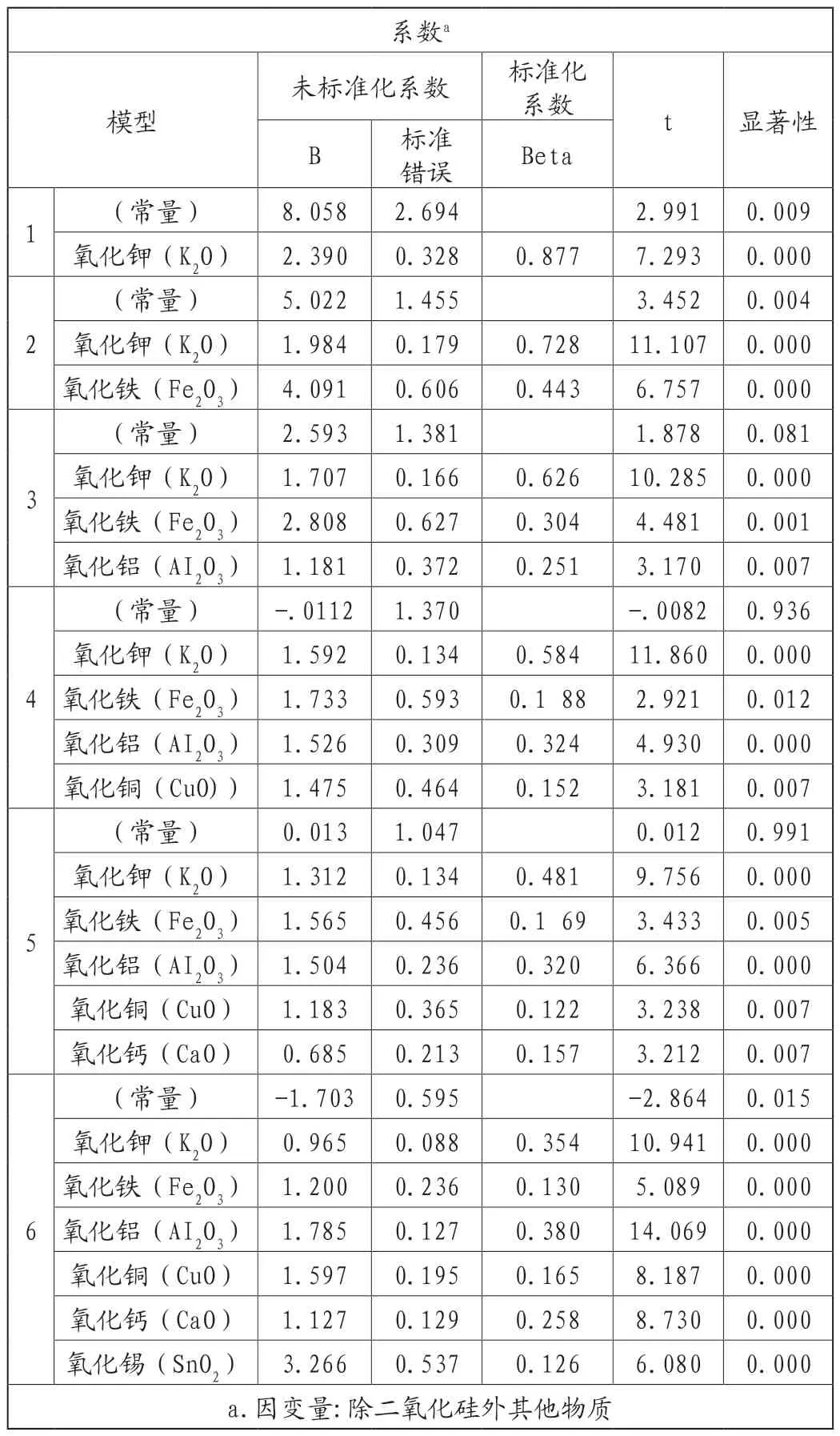
表4 化学成分之间的回归性分析

为了预测SiO2的风化前的含量，利用t检验分析。从表5可以看出，k值得莱文方差满足k＞0.01，即k的数据方差齐性良好。使用其t检验的平均值差值，详见表5，通过式（2）可以对风化前的SiO2值。

表5 二氧化硅的独立样本检验

利用上文得到的线性关系赋值以k的风化变化倍数，拟带入风化后的各线性相关数据，通过式（3）求出k值，并将k值赋以各相关数据，通过式（4）便可得到各个值的风化之前含量，如表6所示。

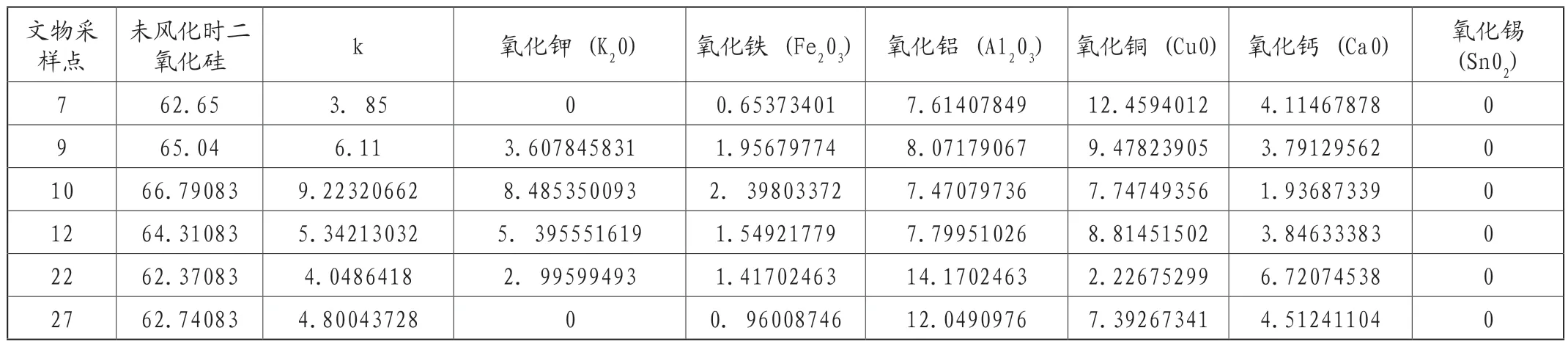
表6 高钾类[2]风化前化学成分预测

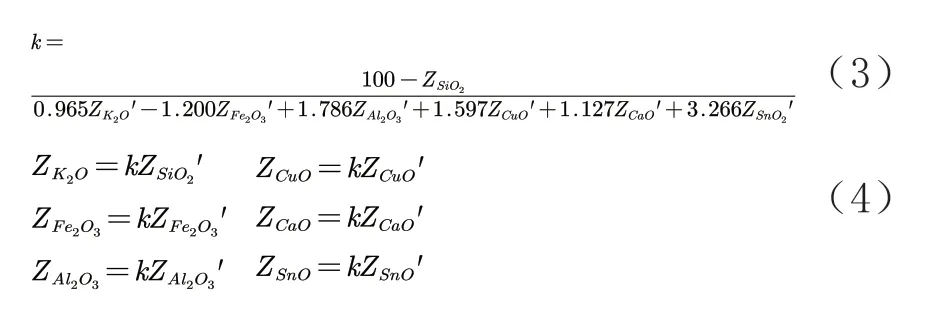
(2)问题二：模型的建立与求解

玻璃文物的化学成分作为高钾类和铅钡类文物划分的重要因素，通过SPSS将化学成分作为二阶聚类的聚类变量进行聚类分析，聚类效果见图。

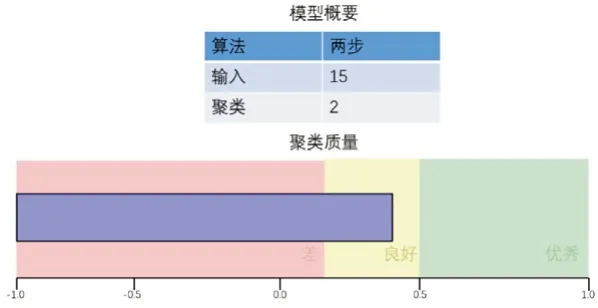
图1 二阶聚类输入15组玻璃制品，聚类为两组，聚类的质量为良好

二阶聚类效果良好，将二阶聚类的结果与高钾类与铅钡类分类的结果进行频率拟合分析，结果见下表7。

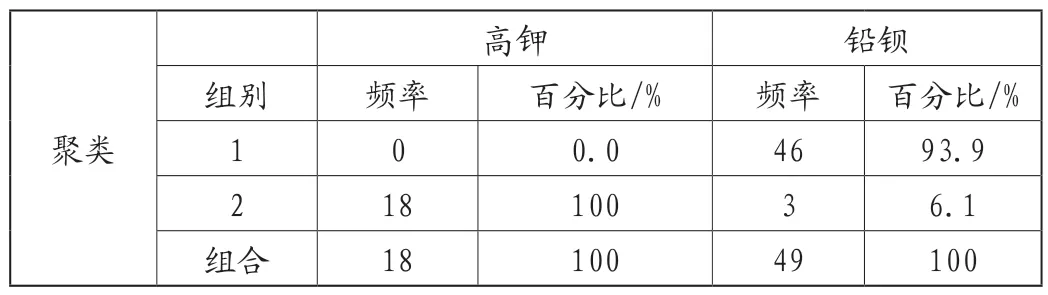
表7 高钾类与铅钡类聚类出现频率

频率表可以看出，聚类结果和原分类结果拟合较好，因此可通过二阶聚类并依照聚类预测变量分析表可以得出，结果见图2。

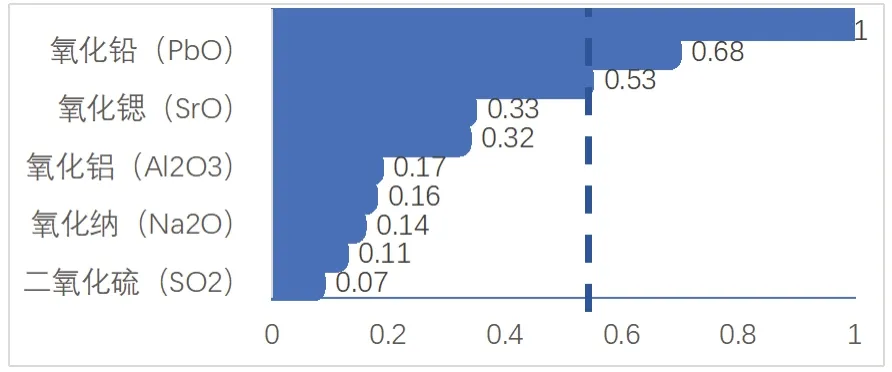
图2 将玻璃文物进行二阶聚类为2组，图为预测变量的重要性柱状图

经上述模型可得，SiO2、PbO、P2O5、SrO和BaO对聚类产生重要的影响，可作为高钾玻璃和铅钡玻璃的分类规律。

(3)问题三：模型的建立与求解

由表8的数据玻璃制品所含化学成分共有14种，并以此建立Fisher多分类判据进行降维分析，通过SPSS得出分类的可信度与相关数据。

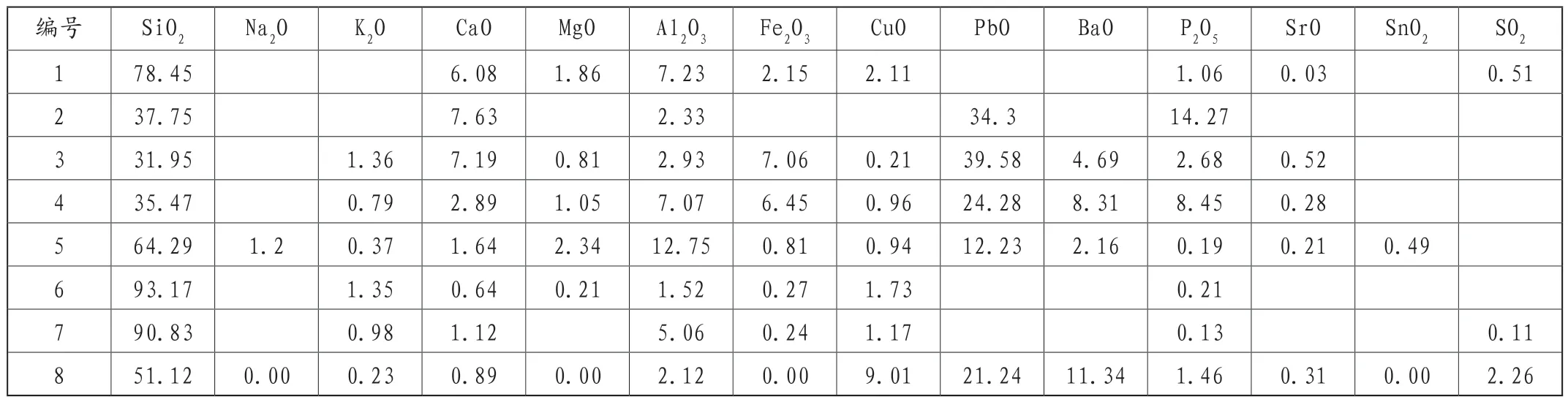
表8 部分典型采样点的采集成分占比

由Fisher分类结果表可得，其对原始数据与高钾和铅钡类分类的结果重合度达到100%，为防止过拟合的现象，进行80%的训练组和20%的验证组进行多次分类，均得到100%的重合度，因此可以Fisher多分类判据进行分类，得到未标准化典则判断函数系数如表9。

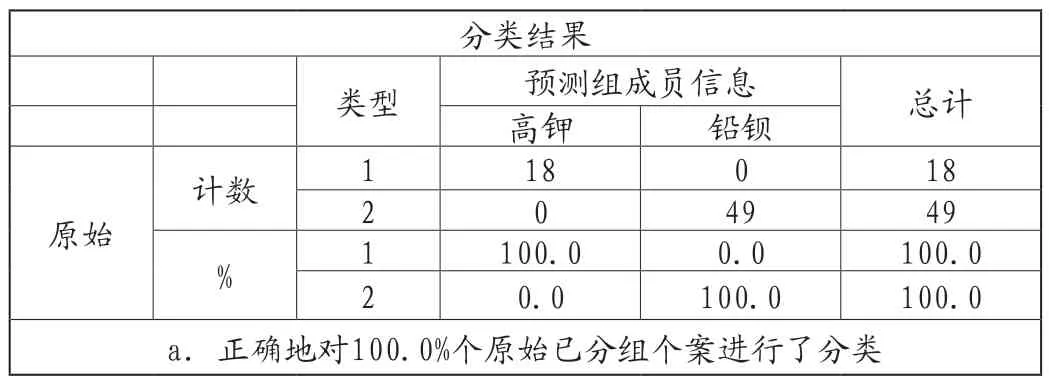
表9 Fisher分类结果表

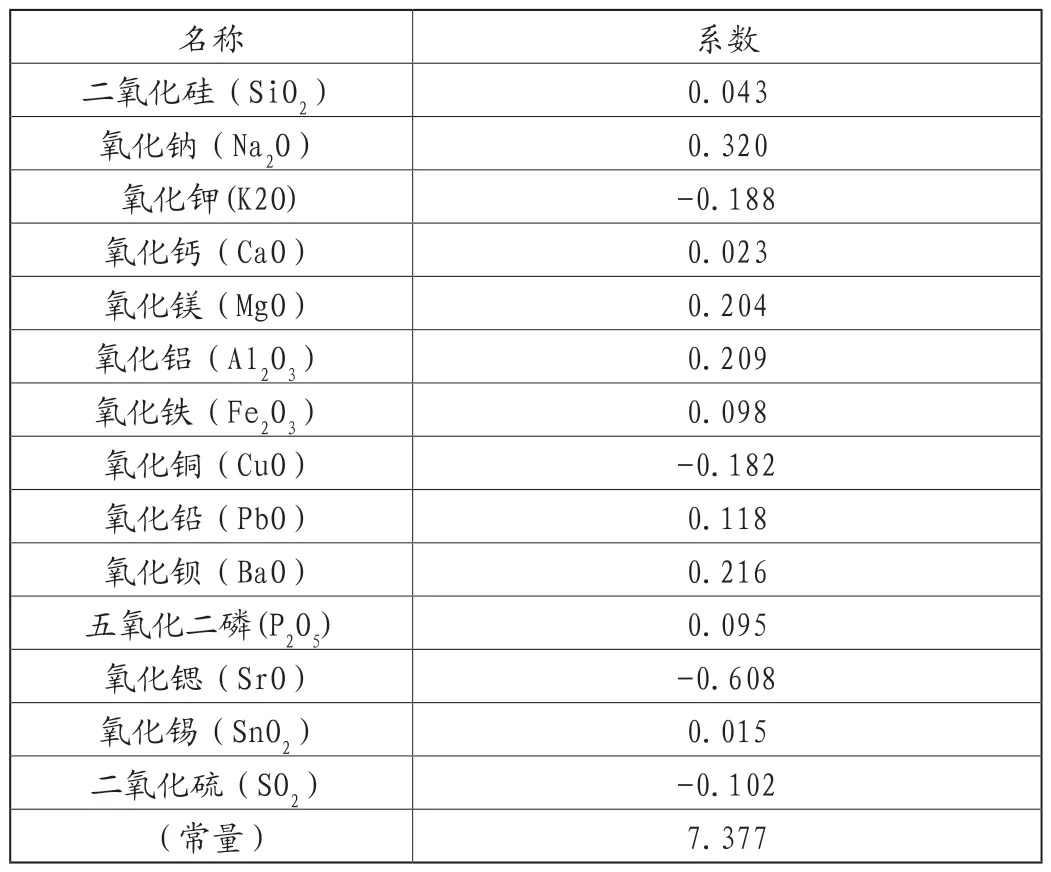
表10 未标准化典则判断函数系数

由未标准化典则判断函数系数得典则判断函数：

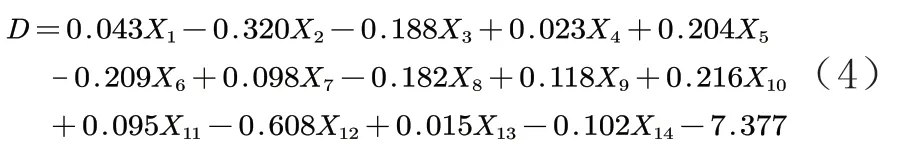
其中，将玻璃制品所含上述化学成分代入式（4）中，若结果小于0，分为高钾组；反之分为铅钡组。

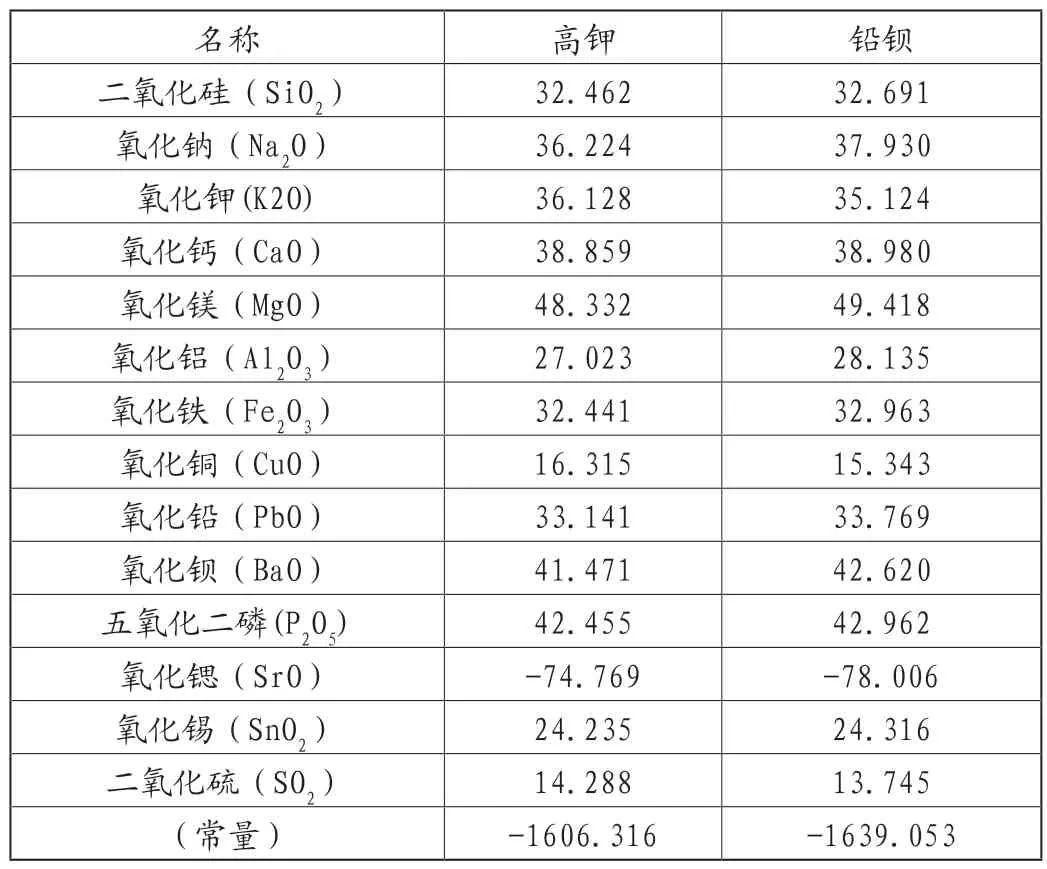
表11 未标准化典则判断函数系数

由分类函数系数得到Bayes判别式：

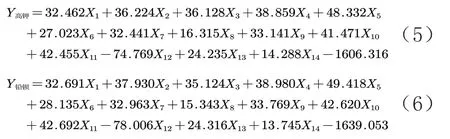
由Bayse判断式性质可得，化学成分代入两式之中，即其在与大者所在的类别。

通过上述玻璃分类模型，即根据式子（4）（5）（6）对未知玻璃制品文物进行分析，得到以下分类表格。

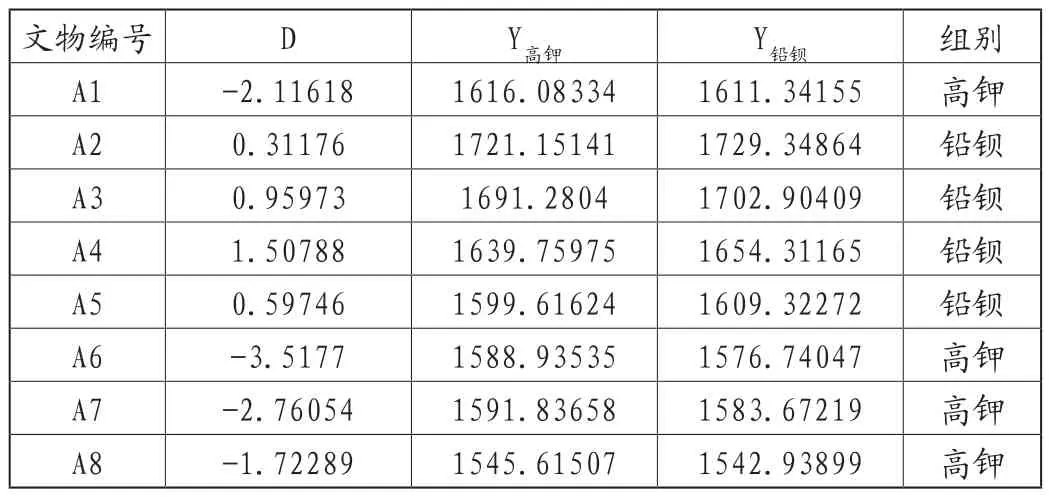
表12 未知文物分类表

4.模型的评价

模型一分析出其相关性和容差值。利用t检验，发现铅钡莱文方差齐性，直接利用平均值差值进行计算。而高钾的莱文方差不齐，便利用SiO2的不变性，巧妙地将风化程度合理量化，通过对其余下的总成分与各个化学成分进行线性回归分析，滤除无关量之后，利用通过t检验预测出风化前的SiO2含量，反推出与之线性相关的主要化学成分风化前的含量。但是存在某些线性程度不好的变量无法进行分析求解的缺点，因此需寻求能够将非线性变量进行线性化的方法。

模型二通过二阶聚类的方法，聚类效果良好，通过聚类结果和高钾铅钡类的分类进行拟合，拟合效果达到93.9%。

模型三采取了博克斯描述，利用组内协方差矩阵，得到了其费希尔系数以及非标准化系数。拟合程度非常良好，可以预测出采样点是否风化。

5.结语

本模型通过对一些基础元素进行分析可以得到较为良好的预测效果，对古代玻璃成分的分析具有辅助帮助。