基于CEEMDAN和SVM的混凝土破坏状态声发射信号识别
2023-02-06栾亚伟胡宝文白延杰
宿 辉,栾亚伟,胡宝文,白延杰
(1.河北工程大学水利水电学院,河北 邯郸 056038; 2.河北省智慧水利重点实验室,河北 邯郸 056038)
随着我国水利建设不断发展,越来越多的混凝土材料被应用于水利工程中。混凝土状态直接决定了水利工程的安全性。因此,混凝土材料早期破坏状态的识别诊断对水利工程的安全运行至关重要[1-2]。声发射技术是目前一种较成熟的无损监测技术,近年来被逐渐用于探寻混凝土破坏状态监测方面的问题[3]。通常对包含混凝土内部损伤信息的声发射信号进行滤波处理,可以精准地提取混凝土破坏过程中的相关参数,进而获得混凝土的损伤信息[4]。例如:袁明等[5]采用快速傅里叶谱变换和小波包分解方法,分析了混凝土裂缝扩展过程中声发射信号,发现混凝土宏观裂纹波形相对于微观裂纹波形更为复杂;赵奎等[6]应用集合经验模态分解(EEMD)及单通道盲源分离(SCBSS)方法对岩石声发射信号进行了滤波处理,发现该方法可以有效保护滤波后声发射信号的频域信息,但该算法添加的高斯白噪声会影响声发射信号的分解。由于傅里叶变换和小波分解法[7]并不能对非平稳的声发射信号进行完全的去噪处理,Torres等[8]提出了自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)方法,其通过对各阶残余量添加自适应白噪声,可有效获取一定数量不同频率的自适应特征模态(IMF)分量,且重构误差趋于0,因此,其对非线性时间序列的分解效果更好。
与传统的神经网络[9]和随机森林[10]等机器学习方法相比,支持向量机(support vector machine,SVM)方法[11-12]的优势在于:适用于小数量样本学习,简化了通常的分类问题,具有很好的鲁棒性。因此,SVM可以有效解决复杂非线性问题中的预测难题。例如:吴鑫等[13]将声发射信号的能量、幅值等特征参数输入神经网络模型中,减小了岩石声发射事件源定位误差;吴贤国等[14]把混凝土材料用量作为参数输入到RF-SVM模型中做回归预测,得到的预测结果精度接近实测值。
本文将CEEMDAN方法与SVM方法耦合使用,提出了一种混凝土破坏状态声发射信号耦合识别模型,探究其对混凝土破坏阶段特征提取的可行性和预测混凝土破坏阶段的准确性。
1 试验方案
1.1 试验材料与方法
为了保证试验的准确性,本次试验混凝土试块规格为100 mm×100 mm×200 mm,水泥为太行山牌P·O 42.5普通硅酸盐水泥,粗骨料为5~15 mm连续级配的碎石,细骨料为当地河砂筛选出,粉煤灰选自当地电厂生产的Ⅱ级粉煤灰,减水剂采用聚羧酸高性能减水剂。
在YH-60B型混凝土标准养护箱养护,养护湿度在95%以上,温度设定为(20±1)℃,养护龄期分别为1 d、3 d、7 d和28 d,强度等级为C30,1 m3混凝土配合比参数包括:水胶比0.42,水198 kg,水泥424 kg,粉煤灰47 kg,碎石1 186 kg,砂582 kg,减水剂1.2 kg。试件共计4组,每组3个试件作为平行试验,共计12个试件,分别对其进行声发射单轴压缩试验,计算各组试件的平均值,当一个试件抗压强度与平均值超过15%时,重新做试验。最后从中选取养护龄期为28 d的工况进行研究。
1.2 试验仪器
加载系统为TAW-2000微机伺服三轴试验机,此次加载方式为位移控,加载速率为0.1 mm/min。声发射系统采用PCI-2型多通道高速采集声发射试验仪,传感器采用R6-a型,频率带宽范围为10~110 kHz,声发射门槛值38 dB,峰值定义时间50 μs,采样率设定1 MSPS,撞击定义时间100 μs,闭锁时间300 μs。
2 声发射信号分析
2.1 混凝土损伤信号预处理
在声发射监测过程中将得到能量、幅值等特征参数,其中前者可以很好地反映混凝土在破坏过程中的状态[15]。图1为混凝土在单轴压缩过程中声发射信号能量-时间和荷载-时间变化曲线。值得注意的是声发射能量可以有效评估混凝土裂纹的变化情况,即裂缝越剧烈,能量越大。
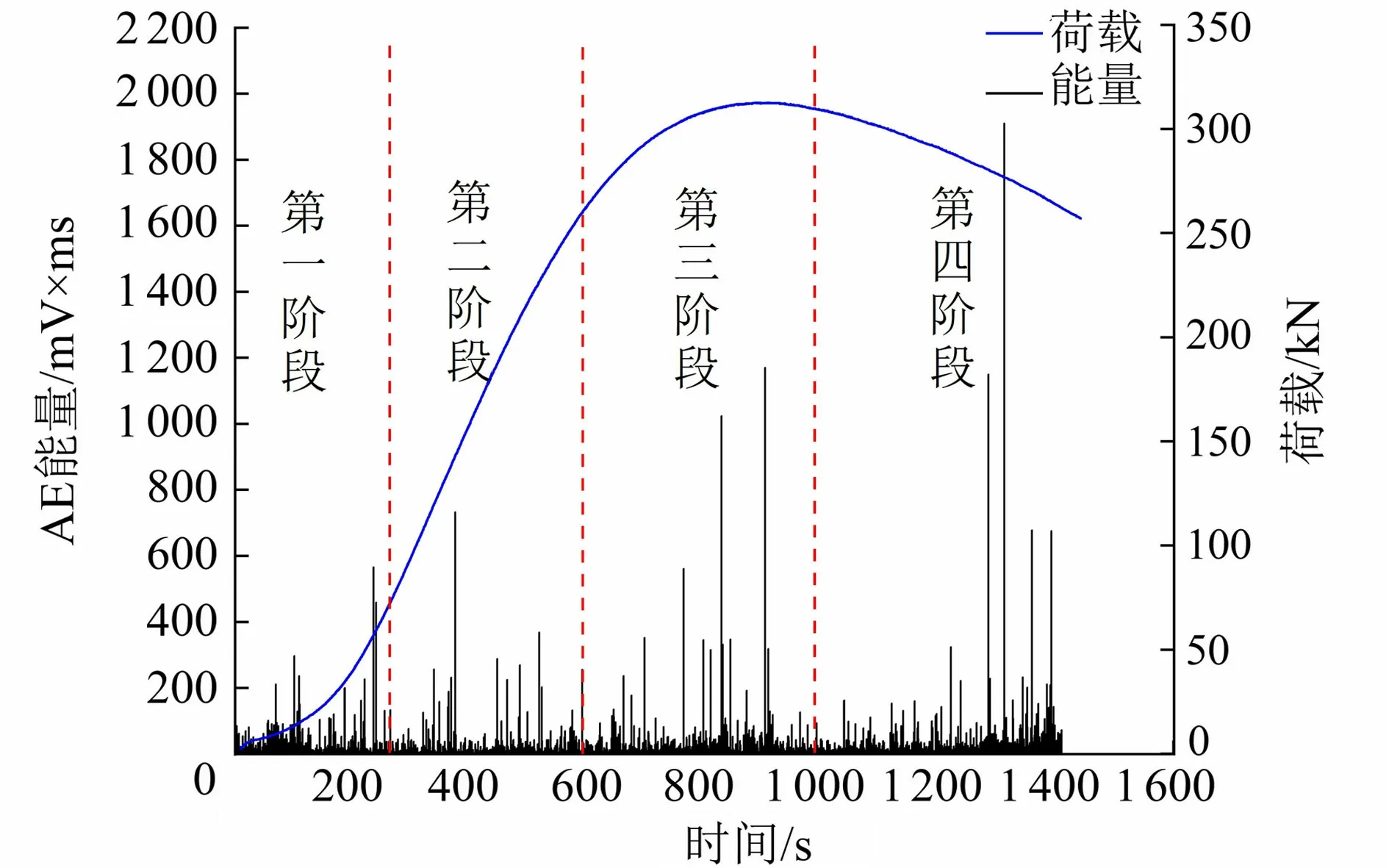
图1 能量-荷载-时间曲线
图1表明,在混凝土破坏过程中,混凝土内部的能量在大多数时间处于均衡释放状态,整体呈现“聚集-释放-再聚集-再释放”的演进过程,但在230 s、370 s、915 s、1310 s附近能量曲线存在局部峰值现象,这归因于混凝土将前一时段内聚集的能量集中释放,其突变点意味着混凝土裂纹发展到最剧烈时刻;在加载初期,混凝土中原始存在的微孔隙在荷载的作用下逐渐闭合,产生一定的声发射信号。随着荷载的增大,混凝土中逐渐有裂纹萌生,荷载继续增大,原始的裂纹进一步发展至试件表面,进入最后一阶段,荷载减小,混凝土材料损伤达到极限状态,根据荷载-时间曲线结合峰值出现的位置和裂纹在破坏过程中的变化过程,可以将整个混凝土破坏过程分为微孔隙闭合、裂纹萌生、裂纹发展、裂纹贯通4个阶段,其相关参数见表1。
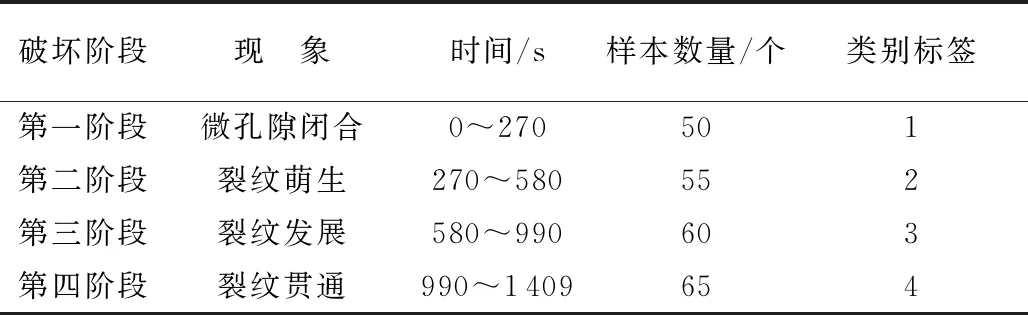
表1 不同破坏阶段的数据集
图2为混凝土破坏过程中声发射幅度分布规律4个阶段中选取的典型信号波形图。通过对不同阶段去噪分解前声发射信号波形的对比发现,随着裂纹的不断发展,声发射信号的幅值逐渐变大、波形复杂程度增大,且在0.01V处存在双波、三波以及难以分辨波形个数的多波。
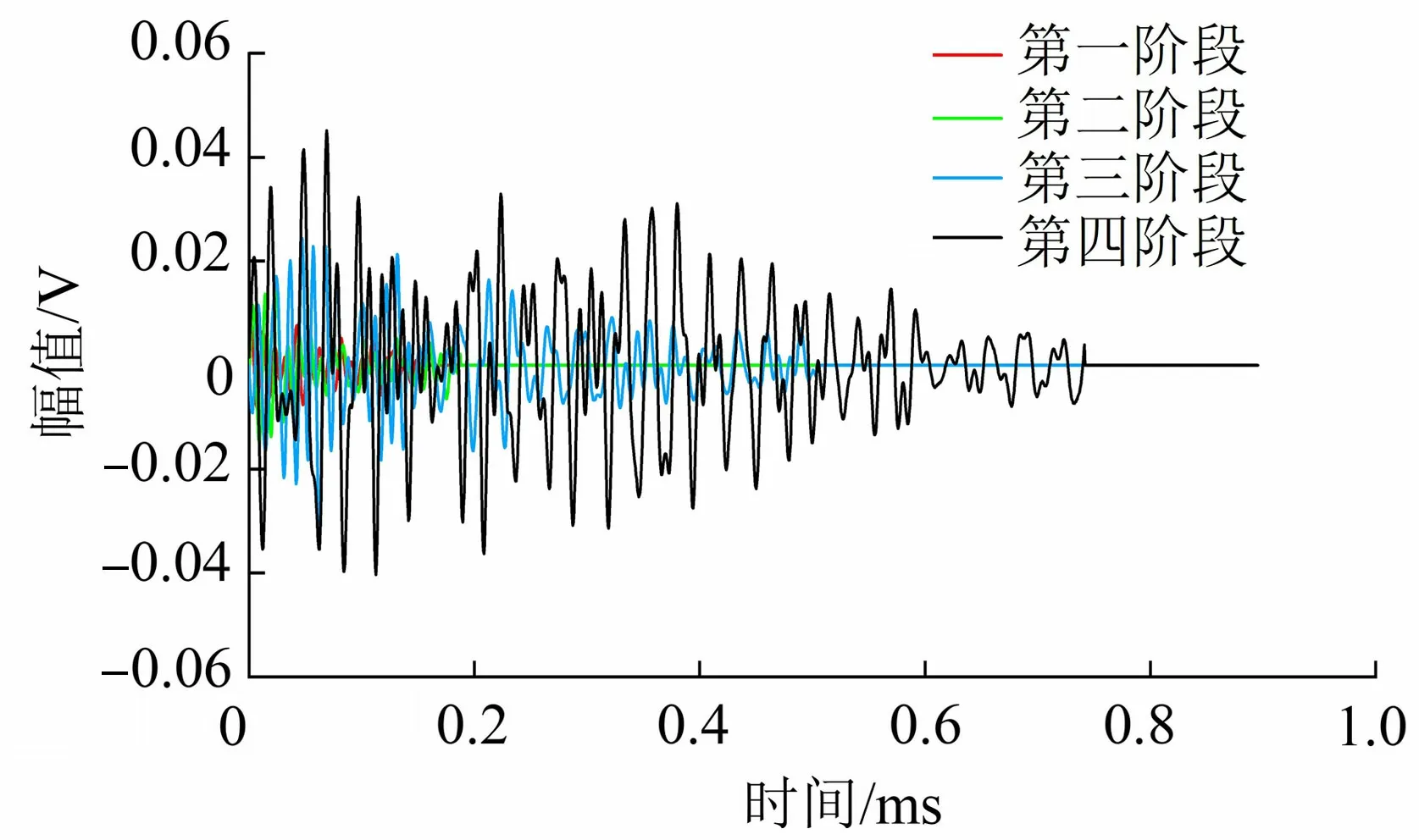
图2 不同破坏阶段典型波形
综合分析表1和图2可知,4个阶段的持续时间依次增加,同时考虑数据的处理量以及SVM方法适用于小数量样本学习,在借鉴王岩等[9]处理声发射信号选取样本的研究成果的基础上,本文确定在第一阶段随机选取50个样本,第二、三、四阶段依次随机选取55个、60个和65个样本。
2.2 基于CEEMDAN的声发射信号分析
基于MATLAB平台,对混凝土不同破坏阶段的声发射信号进行CEEMDAN分解,各个声发射信号均可以分解为10~12个IMF分量和一个残差。
图3为第一阶段中一个原始信号,使用CEEMDAN法对原始信号进行分解,利用分解出的每个IMF分量与原声发射信号的相关系数,可以确定每个IMF分量包含原声发射信号频域信息的程度。IMF1~IMF11分量与原声发射信号的相关系数分别为0.539 4、0.602 1、0.883 7、0.680 1、0.432 4、0.220 9、0.019 9、0.005 3、0.001 5、0.023 3、0.028 4。如果求出的一阶IMF与原信号的相关系数较之前几阶明显小很多,可判定这一阶是假的,应该去掉,计算亦随之停止。从IMF7开始相关程度较之前急剧下降,基本为0,因此IMF1~IMF6包含了原声发射信号中主要频域信息。图4和图5分别为第一阶段原始信号的CEEMDAN的IMF1~IMF6分量及其信号频谱图。
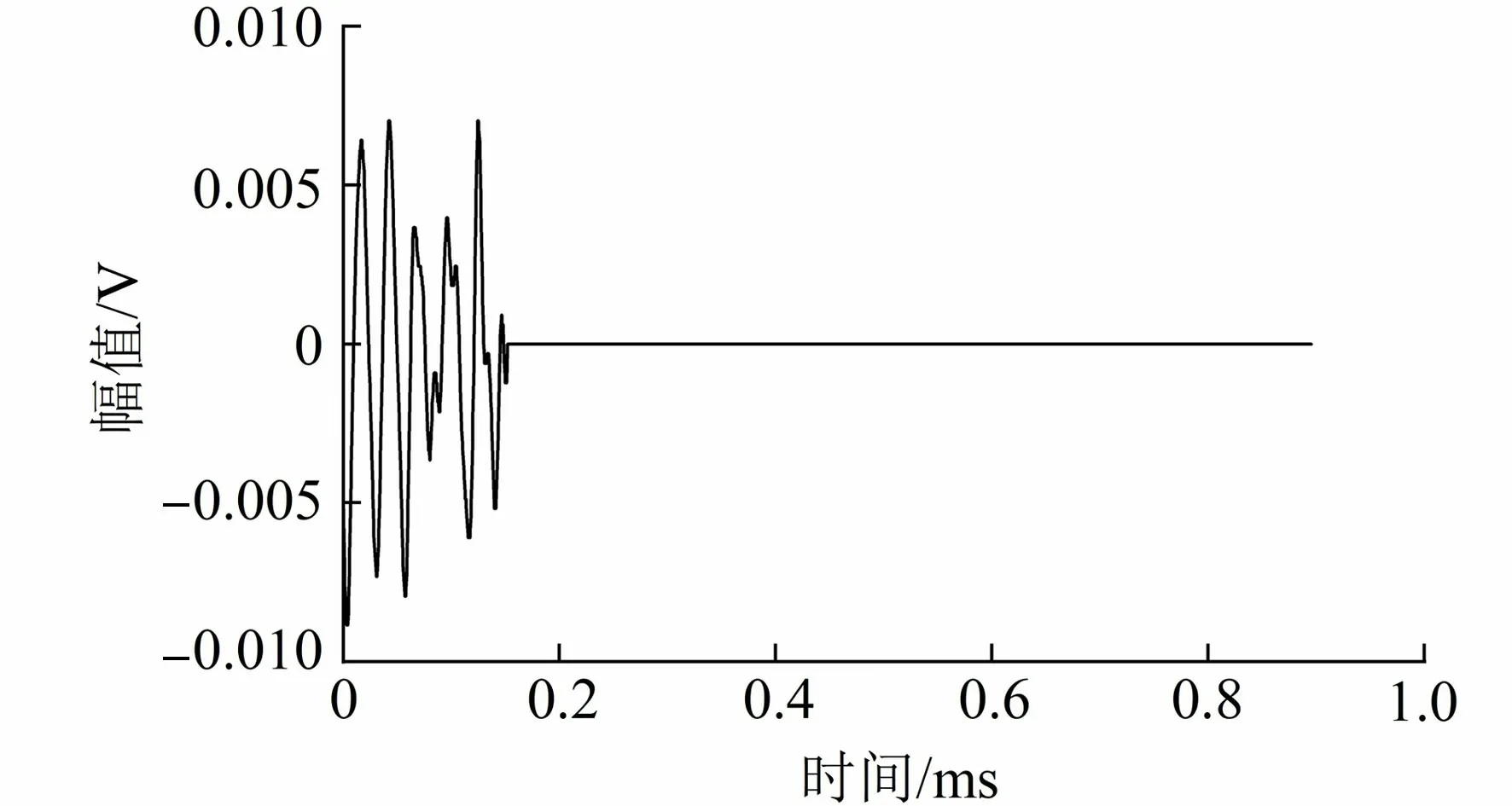
图3 第一阶段原始信号波形
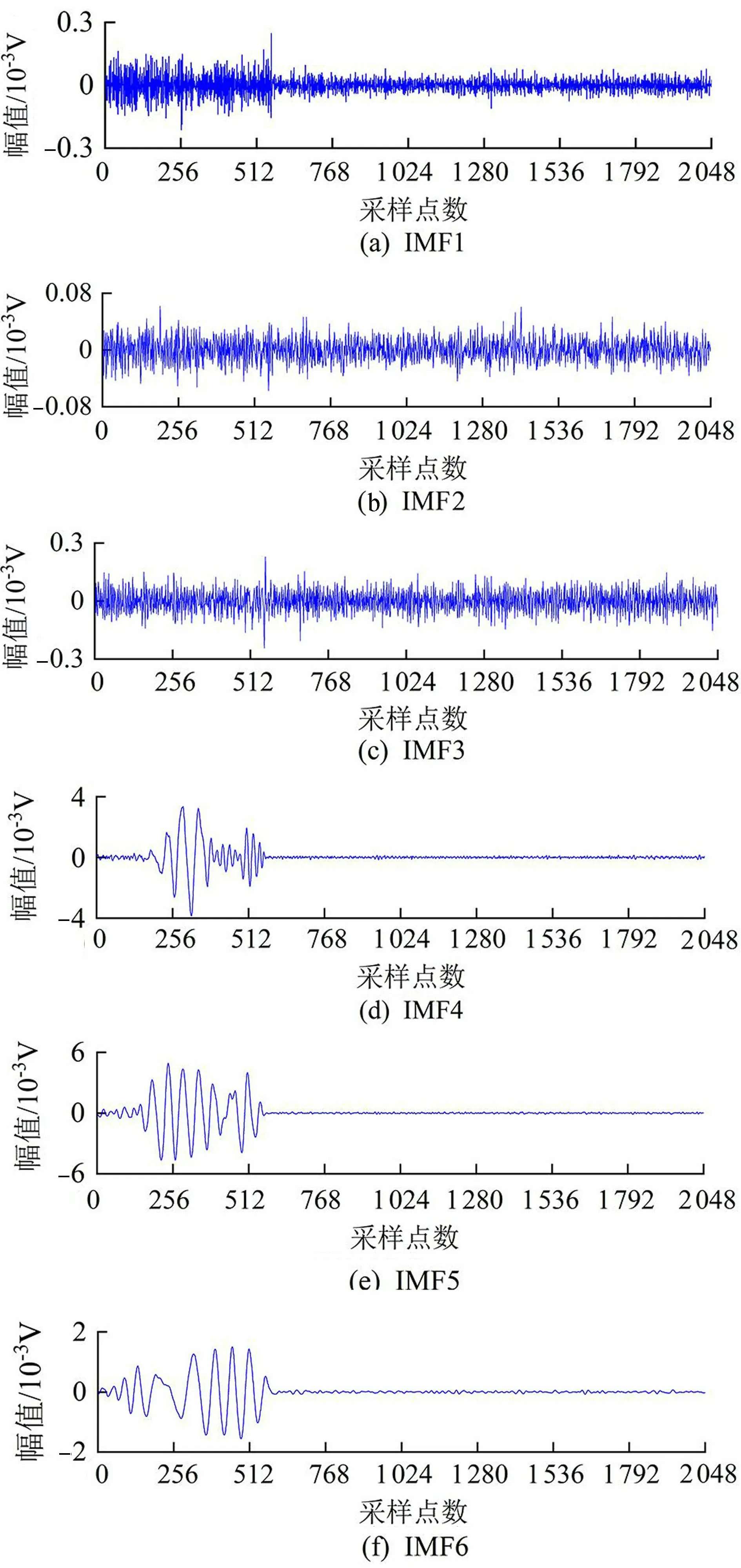
图4 第一阶段原始信号的CEEMDAN分解IMF分量
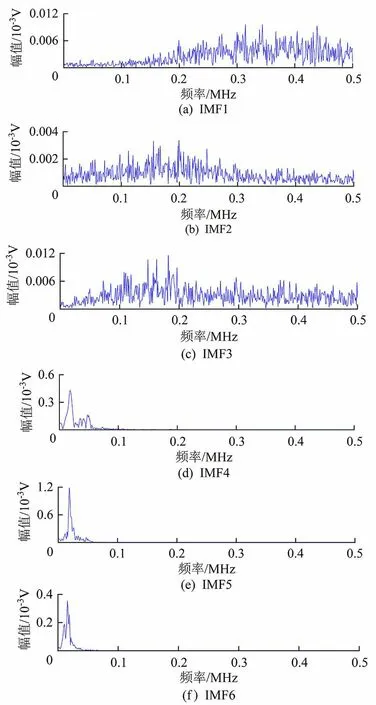
图5 第一阶段原始信号的CEEMDAN分解IMF分量信号频谱
2.3 混凝土破坏声发射信号特征提取结果
利用CEEMDAN分解得到的IMF1~IMF6分量特征参数能量系数Pe和波形系数Cs可以较好地揭示不同破坏阶段特征,其计算公式为
(1)
(2)
式中:χij为第j个IMF分量的第i个数据值;N为信号总数据数;M为IMF分量总数;|χi|表示第i个数据点的绝对值。
值得指出的是能量系数是每个IMF分量占全部IMF分量能量的比值,在不同阶段,其值差异显著;波形系数是波形有效值与波形平均幅值的比值,不同阶段的声发射波形系数也存在差异。混凝土破坏声发射信号特征参数值如表2和表3所示。
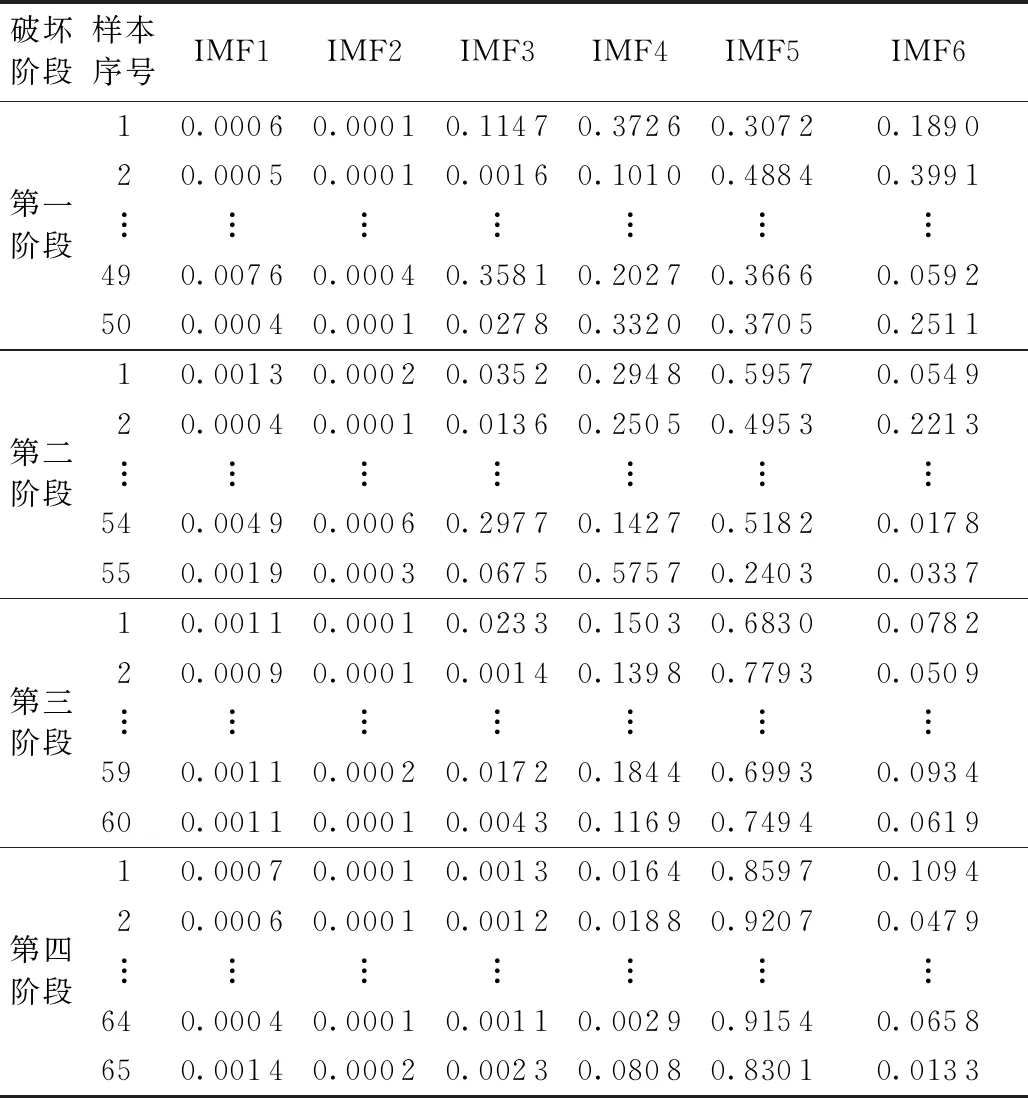
表2 SVM输入特征能量系数
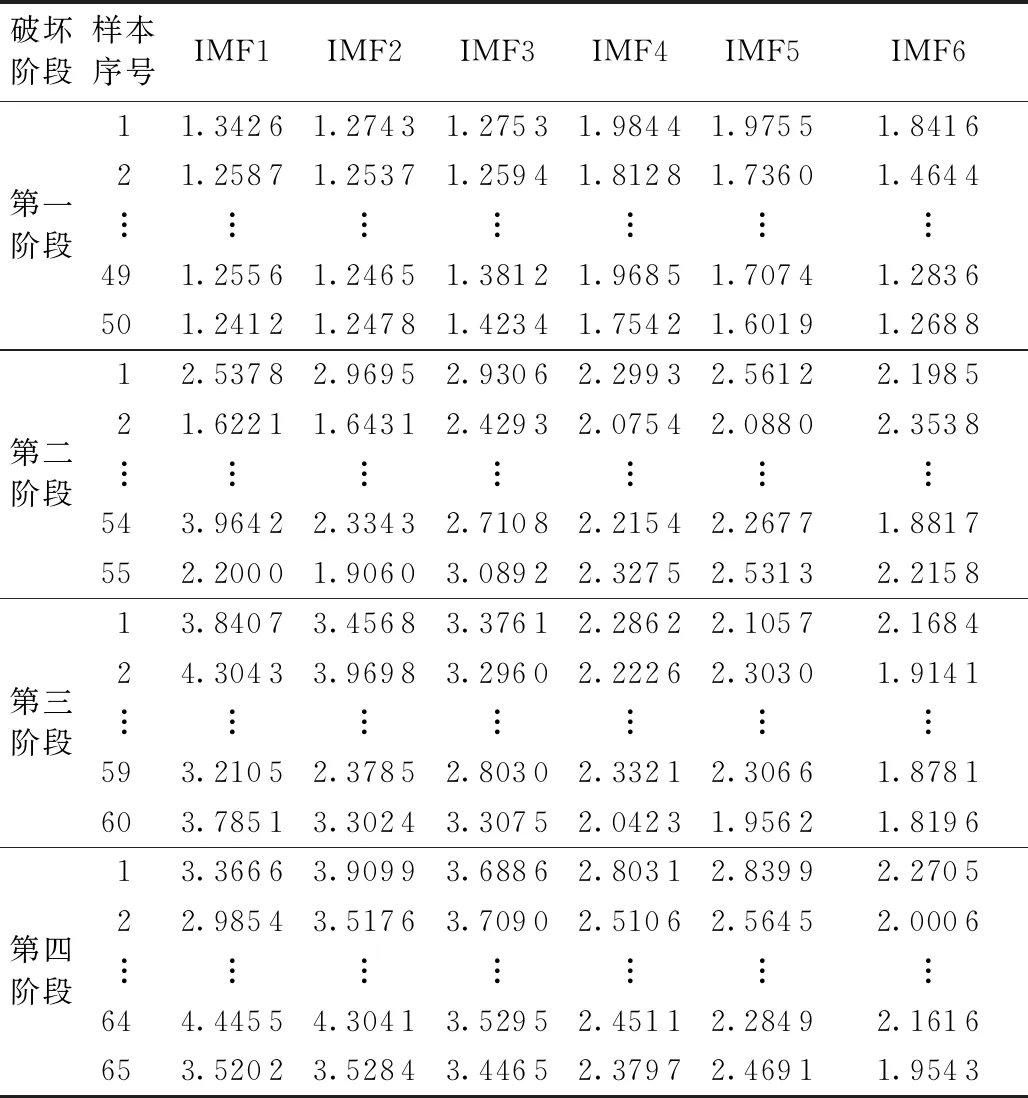
表3 SVM输入特征波形系数
2.4 基于SVM的破坏状态监测
2.4.1数据预处理
数据量纲不统一以及数据偏态分布均会降低SVM的求解速度和模型精度。因此,利用Python软件中的StandardScaler对混凝土破坏声发射信号原始数据进行归一化和标准化处理,并将其输入到SVM中,其计算公式为
(3)
式中:X为原始数据;μ为均值;σ为标准差。
2.4.2网格搜索和交叉验证的参数优化
由于混凝土破坏声发射数据具有高度非线性特征,在SVM训练测试过程中,核函数选择径向基核(RBF),并利用网格搜索法寻找出最优参数惩罚因子C和g。此外,考虑到训练数据对参数的影响较大,且前一阶段的最优参数将会随之改变。因此,采用K-CV交叉验证与网格搜索相结合的方式对每组(C,g)参数进行优选,即将训练数据分为4组,其中3组作为训练集,剩余1组作为预测集,最终优选得到4个模型,并将其分类准确率的平均值视为交叉验证的评估指标。
图6为能量系数和波形系数寻优三维等高线图。SVM方法利用少量样本就可以完成训练学习,为了降低预测样本数量不足易于造成的结果偶然性,故本文选择每个阶段的前60%作为训练样本,其余作为预测样本,且把各信号分量IMF1~MF6的能量系数和波形系数作为SVM的输入特征参数。SVM的输出分为4类,分别为第一阶段、第二阶段、第三阶段和第四阶段。
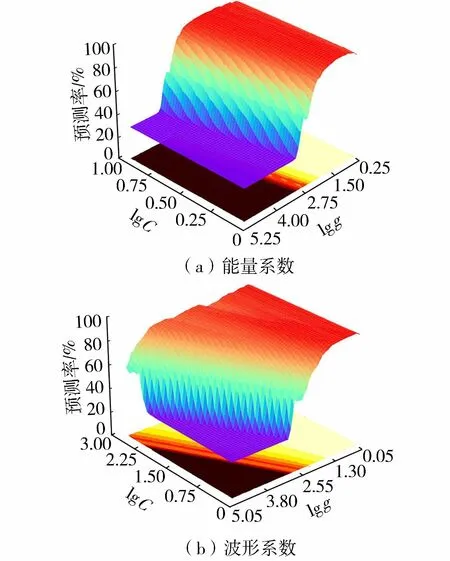
图6 能量系数和波形系数寻优三维等高线
表4为混凝土破坏状态预测结果(能量系数和波形系数分类结果)。由表4可知,将能量系数作为特征参数时,经过网格搜索和交叉验证最终确定参数C的取值为8.3,参数g的取值为0.09,其准确率高达92.39%;将波形系数作为特征参数时,经过网格搜索和交叉验证最终确定参数C的取值为1.02,参数g的取值为1.88,其准确率高达91.30%。
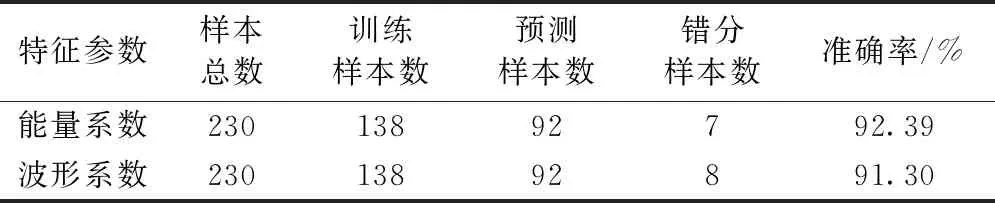
表4 能量系数和波形系数分类结果
3 结 论
a.基于CEEMDAN和SVM方法对混凝土破坏状态识别是可行的,且利用IMF分量和原信号的相关性可有效剔除虚假分量。
b.利用网格寻优和交叉验证方法优化SVM参数,可以提高诊断精度。
c.有效IMF分量的能量系数和波形系数作为特征参数时,其预测率分别为92.39%和91.30%,两者均可以较优地揭示混凝土破坏的损伤特征。
d.提出的CEEMDAN与SVM耦合方法可有效进行混凝土破坏状态的识别,研究成果可为评估混凝土结构安全状态提供可靠的理论依据。
