基于SSA-BP算法的锚护机器人误差补偿研究
2023-02-06史光亮马祺杰王海燕张宁波
史光亮,马祺杰,王海燕,张宁波,李 波
(1.中煤华晋集团有限公司王家岭矿,山西 运城 043300;2.中国煤炭科工集团太原研究院有限公司,山西 太原 030006;3.山西天地煤机装备有限公司,山西 太原 030006;4.中煤(天津)地下工程智能研究院有限公司,天津 300131)
0 引 言
锚护是矿山开采中的关键性工序之一,锚护机器人更是智慧矿山不可缺少的设备。利用锚护机器人不仅可以减少开采支出、加快支护速度、提高经济效益,还能够通过无人支护,提高井下作业安全性[1],实现全自动、智能化作业需要超高的精度,因此,作业精度就成为衡量锚护机器人性能的重要指标。
生产、装配、碰撞或磨损都会造成锚护机器人末端精度降低,负载工作导致机身变形也会影响末端精度[2],这就需要进行误差补偿。国内外学者的研究已经获得了一些成果,例如给机器人关节空间直接补偿[3]、引入特有误差因素完善原有误差模型[4]、利用智能算法误差补偿[5]等。目前,各大煤矿使用的仍是掘锚机、运锚机等配套的机载式钻架,该类型钻架存在工作范围有限、不灵活、不能实现全自动锚钻功能等缺陷,边帮则使用手工钻人工支护,远没有达到锚护机器人的智能化支护水准。国外只有SANDVIK集团的掘进凿岩台车和凿岩支护钻机两种设备可以实现多关节活动、自动打孔、铺网、锚杆紧固,但是由于技术保密,无法获得数据。而国内方面,中国煤炭科工集团太原研究院有限公司制造出了两臂智能锚杆钻车,填补了国内锚护机器人的空白。
因此,本着省时省力、支出少、安全性高的施工原则,本文在现有研究的基础上提出用麻雀算法改进BP神经网络尝试误差补偿,并通过几种算法的相互对比,证明该方法的可行性。
1 误差模型
1.1 误差模型的建立
根据Chasles定理[6],可以运动旋量表示刚体运动。设置参考位姿和形态,如图1所示。在没有其他误差干扰的情况下,各个关节轴线处产生的平移或者旋转误差都可以误差旋量表示,其在世界坐标系下书写为ξe1(0),ξe2(0),...,ξen(0)[7]。进一步分解可以发现,这些误差旋量和关节轴线经过旋转、平移或者螺旋运动的结果一致,因此广义上可以把其看作刚体的移动副或者旋转副,由此可得锚护机器人含误差旋量的指数积公式[8]见式(1)。

图1 运动副坐标误差
T(θ)=
(1)
根据相关资料可知[9-10],大部分末端误差都是由几何参数误差造成的,占总误差的80%。由陈杰[9]的误差建模分析可知,旋转角度误差、运动副轴线偏转、偏移误差这三种误差对锚护机器人末端位姿精度影响最大,因此应使用这三种误差因素建立误差模型。为了更加方便地分析计算过程,假设三种误差值分别为0.01°、0.01°、0.1 mm[11],各关节添加误差见表1。
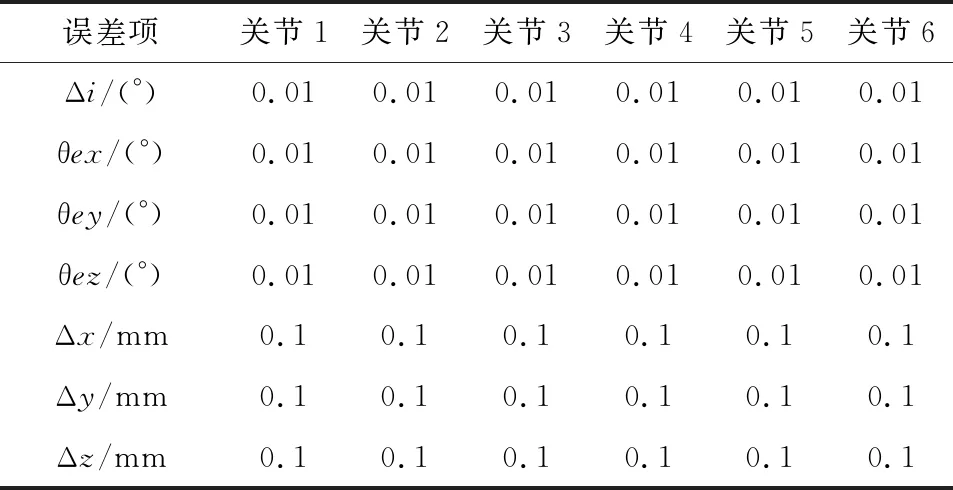
表1 关节误差值
如果把添加的误差看作旋量运动的结果,则误差经过矩阵变换后可表示为式(2)[12]。
T=transl(0.1,0.1,0.1)grpy2r×
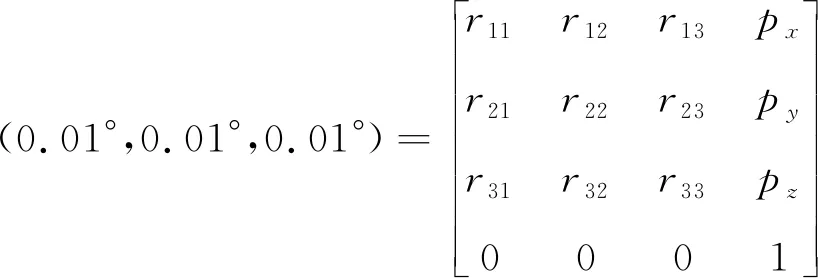
(2)
由T可求得ωe、ve,进而求误差旋量ξe见式(3)[13]。
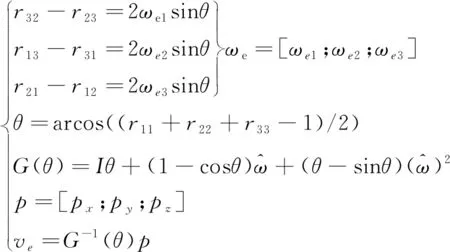
(3)
根据伴随矩阵的定义可得式(4)。

(4)
综上可得完整误差模型公式[14],见式(5)。
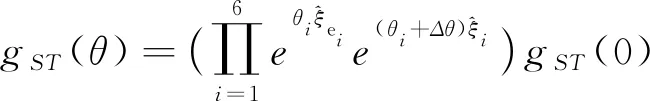
(5)
1.2 误差模型的验证
在建模软件中搭建带误差的锚护机器人虚拟样机,测量后可知虚拟样机初始位姿和数学工具中计算结果相一致,如图2所示。在锚护机器人的工作空间内随机抽取10组关节角向量θi=[θ1,θ2,θ3,θ4,θ5,θ6](i=1~10)来验证误差模型的正确性。首先将10组关节角向量依次代入数学工具仿真软件的误差模型计算出对应的锚护机器人末端位置坐标Ti=(TX,Ty,Tz),然后将这10组关节角向量依次代入三维模型仿真平台中带误差模型的虚拟样机,求出相应的10组末端位置坐标ti=(tX,ty,tz)。通过坐标Ti和ti计算出两者之间的“相对距离”,以两坐标点之间的相对距离作为两坐标点之间的误差值,计算结果见表2。 由表2可知,软件计算和虚拟样机仿真的结果基本一致,因为软件的数值运算存在精度限制,因此表2中产生的3×10-7~4×10-7mm的误差为合理误差,可忽略不计,本文提出的误差建模方法的正确性得到了验证。

图2 初始位形测量图

表2 末端位置对比表

续表2
2 基于SSA-BP神经网络误差补偿法
2.1 麻雀算法
麻雀算法就是模拟麻雀觅食过程从而获得优化问题的解[15],群集用矩阵见式(6)。
X=[x1,x2,…,xN]T,xi=[xi1,xi2,…,xiD]
(6)
式中:N为规模数;i=(1,2,…,N);D为变量维数。适应度计算公式见式(7)。

(7)
式中,fxi为适应度值。位置更新公式见式(8)。

(8)
式中:t为现阶段重复反馈次数;T为全局重复反馈次数;α为(0,1]随机数;Q为标准正态分布数;L为1×d的矩阵,矩阵元素均为1;R2为危险值;ST为安全值。位置更新公式见式(9)。

(9)


(10)
式中:β为满足数组平均数等于0且与平均数之差平方和的平均数等于1的常态分布;K为在-1到1范围内的任意数,可以用来表示粒子运动方向;fi、fg、fw分别为当前个体适应度值、当前全局最优值和当前全局最差值[17]。
2.2 SSA-BP算法误差补偿原理
使用麻雀算法的适应度值更新BP神经网络的权值和阈值[18]。由于预警和惩罚机制的存在,不但加快了BP模型的收敛速度,还避免了过早收敛,解决了局部最优的问题。通过计算麻雀适应度值来更新BP神经网络权重和阈值,把更新后的权数和临界值代入BP模型,将理论模型中的关节角θ和带误差的实际关节角q分别作为导入和导出让BP神经网络自我学习[14]。给定一组关节角度q,将其代入误差模型中求得实际位姿T,然后将T代入不含误差的逆运动学模型中求得理论关节角θ,最后把理论关节角θ和实际角q作为BP神经网络反向学习的导入和导出。BP神经网络训练模式如图3所示。

图3 BP神经网络训练图
直接使用q和θ这两组关节角训练神经网络的优势为当给定关节角理论值θ后神经网络会直接预测出关节角实际值q,既省略了求关节角补偿角Δq的步骤,又补偿了锚护机器人的误差,简化了计算过程,减小了补偿后的误差值,BP神经网络学习的过程如图4所示。

图4 BP神经网络学习过程
3 锚护机器人误差补偿仿真与实验
3.1 仿真结果与分析
首先使用数学工具进行仿真测试,在关节空间随机选1 000组关节角训练SSA-BP神经网络,测试后得到最佳结构参数;接着输入输出层的节点数取6,隐含层的节点数取8,进行100次迭代,学习效率设为0.1,目标误差设为10-4。SSA-BP补偿模型的训练情况如图5所示。由图6可知,使用训练好的SSA-BP补偿模型补偿后6个关节角误差下降到-0.004 9~-0.003 5。

图5 SSA-BP训练图
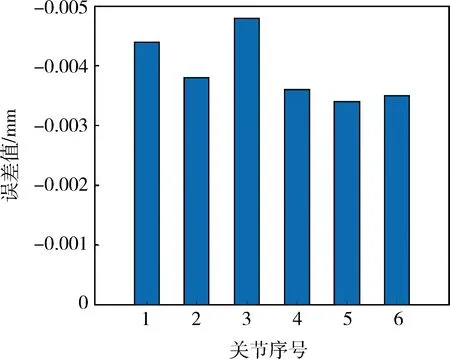
图6 SSA-BP误差补偿预测图
为体现本文补偿方法的准确性和优越性,选择两种模型与其进行对比,分别选择BP神经网络补偿法和粒子群算法改进BP神经网络补偿法(PSO-BP)。使用BP神经网络补偿法和PSO-BP神经网络补偿法进行误差补,补偿后各关节角预测误差如图7和图8所示。最后使用这三种方法直接对末端的位置误差和姿态误差进行补偿仿真,补偿结果如图9所示。

图7 BP误差补偿预测图

图8 PSO-BP误差补偿预测图
由图6~图9可知,用优化算法改进后的BP神经网络进行误差补偿效果更好,且相对于粒子群优化算法,麻雀优化算法改进后的BP神经网络补偿效果更好,补偿后末端位置误差减小到5×10-3mm之内,姿态误差减小到10-5°之内。精度提高了80%,证明了SSA-BP算法在误差补偿应用中的准确性和可行性。

图9 位姿误差对比图
3.2 试验验证与分析
搭建如图10所示的试验平台对SSA-BP神经网络误差补偿方法进行试验验证。其中,试验所用载体为CMM2-25煤矿用全自动两臂智能锚护机器人,其自身带有传感器、编码器等高精度定位测量装置,可以精确地实时监测各个关节角和末端坐标。以左臂第一个关节点中心为世界坐标系原点,以左钻架顶点作为末端执行器点建立运动学模型,运用如图11所示的示教平台进行试验运算。

图10 试验平台

图11 示教平台
在锚护机器人工作空间内取10组关节角,先用示教平台求出锚护机器人末端的位姿的原误差见表3。然后带入SSA-BP神经网络误差补偿法,求出补偿后的锚护机器人末端位姿误差值,结果见表4。通过表3和表4中的数据可知,在SSA-BP神经网络补偿法的作用下锚护机器人末端的姿态误差从1°下降到0.5°以下,位置误差由50 mm降到了10 mm附近,显著提高了末端精度。

表3 原始位姿误差表

表4 SSA-BP补偿后位姿误差
综上所述,无论是锚护机器人终端位置还是锚护机器人终端姿态,优化后的补偿模型补偿效果更好,而且麻雀算法比粒子群算法优化的效果更好,即三种补偿模型中SSA-BP的补偿效果最好。
4 结 语
为了提高锚护机器人井下支护时的锚钻精度,本文使用更加贴合实际物理意义的旋量法建立误差模型。根据麻雀算法收敛速度快、全局寻优能力强、不会陷入局部最优的特点使用SSA-BP神经网络进行在线实时误差补偿。通过虚拟样机和对比仿真证明了SSA-BP算法在误差补偿应用中的准确性和精确性。最通过试验验证,证明了SSA-BP神经网络误差补偿法的实用性和可行性。
