组合模型在基坑监测中的应用研究

杨纪勉

（拓远（福建）勘测规划有限公司，福建福州 350002）

0 引言

选择科学、合理的基坑监测方案是保证基坑安全、施工顺利的重要前提，较好的基坑监测方案能够优化施工方案设计，并为施工安全提供可靠依据。基坑监测的实施能够及时提供施工监测信息，预测可能发生的危机，进而保证建筑物建设质量，有效降低事故发生概率。但在施工过程中，不可避免地会有突发情况，产生不稳定因素。因此，在基坑工程施工中，应始终确保基坑变形量在规定的安全范围内，保证基坑工程及周围建筑物的安全。这就要求要密切监测基坑变形，在施工过程中，以施工监测为基础，运用方法合理分析，最终达到预测的目的。

对基坑工程事故进行分析，可以看出，随着城市化进程的加快，基坑工程事故的发生与以往相比明显增加，特别是在我国东南沿海开放城市中，一些大型基坑工程事故占总量的1/3 左右［1］。这要求更加重视基坑监测，防范此类事故，保护社会资源和人民生命财产安全。因此，如何根据已知的、少量的观测数据，建立准确的预测模型，是当前的研究重点之一［2-3］。基坑监测工程在国外开展得比较早，最早在20 世纪40 年代，Terzaghi 和Peck 等研究人员就开始研究基坑工程，他们运用数学方法，使数学估计理论开始服务于深基坑工程，并在成果中全方位评估工程施工过程中建筑稳定性［4］。20世纪70 年代之前，我国大多数基坑的深度都在10 m 以内；80 年代后期，大型深基坑才开始逐渐增多［5］。面对深基坑变形监测，我国众多专家学者对此进行了深度分析与研究。李宏义分析了基坑变形灰色预警系统［6］，钟正雄建立了基坑监测数据库管理系统［7］。在2001 年，胡友健等建立了监测数据处理与预测报警系统，该系统以GM（1，1）理论构建形变预测模型，以支护结构水平位移、位移与开挖深度比、水平位移变化速率等指标进行险情预报［8］。徐洪钟等建立基坑光纤光栅检测系统，使我国的基坑监测研究事业又更进一步［9］。此外，考虑到利用水准仪、经纬仪等传统测量设备进行基坑监测的不足，张建文开发了基坑工程远程安全监测系统，为基坑工程的施工提供科学建议［10］。近年来，于清华利用线性回归、灰色GM（1，1）模型及二者组合模型进行综合对比，经过验证得出的组合模型结果更为可靠［11］；杜建广在传统AR 模型的基础上，创建了一种基于经验模态分解方法的差分灰色神经网络模型，解决了模型中预测结果精度较低和稳定性较低等问题［12］；针对人工神经网络预测模型存在的不足，邢旋旋提出将附加动量法和自适应学习速率法应用于人工神经网络，建立了基于时间序列和影响因素的BP 神经网络预测模型［13］；谢荣华先探究了曲线拟合、自回归法和指数平滑法在基坑监测中的可靠性，再利用蚁群算法将上述三种模型进行组合，预测结果优于单一模型［14］；侯跃强提出串联式组合模型的概念，介绍了串联式组合模型的两种构建形式，并用实例验证了串联式组合模型的可靠性［15］。

借鉴已有的研究成果，本文利用实际工程案例，对单一模型和组合模型的形变预测精度进行了比较分析。结果显示：相较于单一模型，组合模型的预测结果更为可靠，该结果对基坑工程的实际应用具有一定的参考价值。

1 预测模型

1.1 灰色系统模型

灰色系统理论于1982 年由中国学者邓聚龙提出［16］，经过多年的发展之后，已经成为一门新型的学科结构体系，现已广泛应用于生态、社会等各个领域，发展前景十分广阔。灰色系统将系统的行为看作是随机变化的过程，基于信息的非完全原则，利用原始数据来探究变化规律。然而在实际中，不一定能找到规律或者找到的规律不适用于所有情况，不具有典型性。但是尽管数据离散，在将其累加之后也会出现指数变化规律，这也说明它必然存在内在的客观规律，需要进行深度探究。将数据转化成微分方程，建立数学模型，然后不断对模型优化改进。

GM（1，1）模型是目前使用较为广泛的一种模型，该模型通过将历史数据序列x（0）主次累加，生成新的数列，弱化数据中的随机性，进而提高预测精度。设原始监测序列x（0）=（x（0）（1），x（0）（2），…x（0）（n）），然后按照模型构建原理对x（0）进行一次累加，得到数列x（1）=（x（1）（1），x（1）（2），…x（1）（n）），如式（1）所示：

根据灰色理论对x（1）建立一阶灰色模块的白化形式微分方程，如式（2）所示：

式中：a，u为待求系数。一阶微分方程求解得

式中：

从式（3）可求解出系数向量a、u，再根据初始条件，可得

对x（1）进行逆变还原处理，可得GM（1，1）预测模型方程为

灰色模型通常用后验差检验法检验精度。其精度由均方差比值和小误差概率共同评定。其具体步骤为

设X（0）为原始序列，X（0）为GM（1，1）模型模拟序列，e（k）为残差序列，则有：

残差结果计算完成后，分别计算原始数据序列x（0）和残差绝对值序列e（k）的均方差S1和S2：

其中

然后计算后验差比值C：

最后计算小误差概率P：

根据精度检验要求，均方差比值C尽可能小，指标P尽可能大。

1.2 时间序列模型

时间序列顾名思义就是随着时间变化而变化的，随机的且前后有联系的观测数据，按照时间顺序，排列成一个有序的数列。

时间序列（AR）模型的建立，时间序列1，2，…，n）的自回归（AR）模型为

式中：φ1，φ2，…，φp为自回归模型系数；P为模型阶数。

误差方程为

其矩阵形式为

式中：

在VTV=Min 时，模型参数最小二乘解为

1.3 灰色时序组合模型

每个预测模型都有其适用的条件范围，同时这也代表着每一个模型都有其局限性。若单一模型在预测的过程中，适用条件发生变化，则该模型预测精度将大大降低。此外，单一模型对于信息的利用率较低，无法充分利用有效信息，这也将降低预测精度。

组合预测模型就是将各个单一模型提供的数据信息进行综合，将有限的信息充分利用。它可以避免单一分析方法易受环境因素干扰的缺点，也可以避免由于偶然误差因素造成的数据结果失真。

灰色模型与时间序列模型相结合称为灰色时序组合预测模型。灰色模型是利用原始观测数据，对数据进行累加，弱化数列的随机性，加强数列的规律性，进而达到预测效果，但对随机信号却无法进行处理。时间序列的模型预测不同于灰色模型，它依据时间顺序，利用数据的自相关性建立模型，分析数据规律，从而对未来数据进行预测，但其往往要先进行时序的零均值化和平稳化，才能进行建模。灰色模型与时间序列模型的组合模型可以充分利用两者的优势，先用灰色GM（1，1）模型进行预处理，提取数列的趋势项，再利用AR 模型处理数列的随机残差，这样既可以达到更高精度的预测效果，也可以规避单一模型的不足之处。

两种模型组合方式为

式中：dt为趋势项；为序列Xt的非平稳部分；yt为Xt提取dt后剩余的平稳时序。

2 工程实例

现以一工程实例说明组合模型在基坑监测中的精度。某基坑支护结构为水泥搅拌桩-锚杆，在基坑周围布置了测斜管，某一测斜管的观测结果如表1 所示。

表1 测斜管-2.0 m 处测点水平位移观测值单位：mm

选取前20 期监测数据，分别利用GM（1，1）模型、时间序列模型和灰色时序组合模型对数据进行处理，并将预测结果与实测数据进行比较，结果分别如表2 和图1 所示。

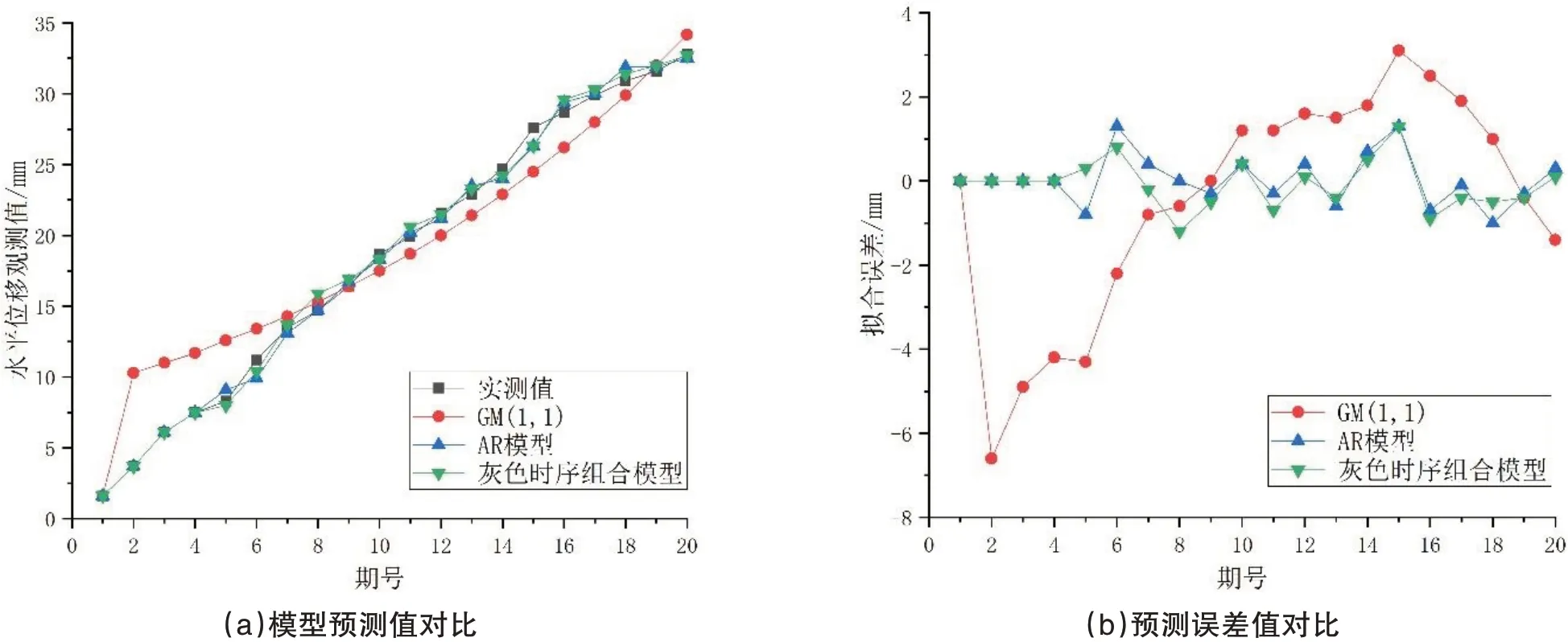
图1 模型预测结果

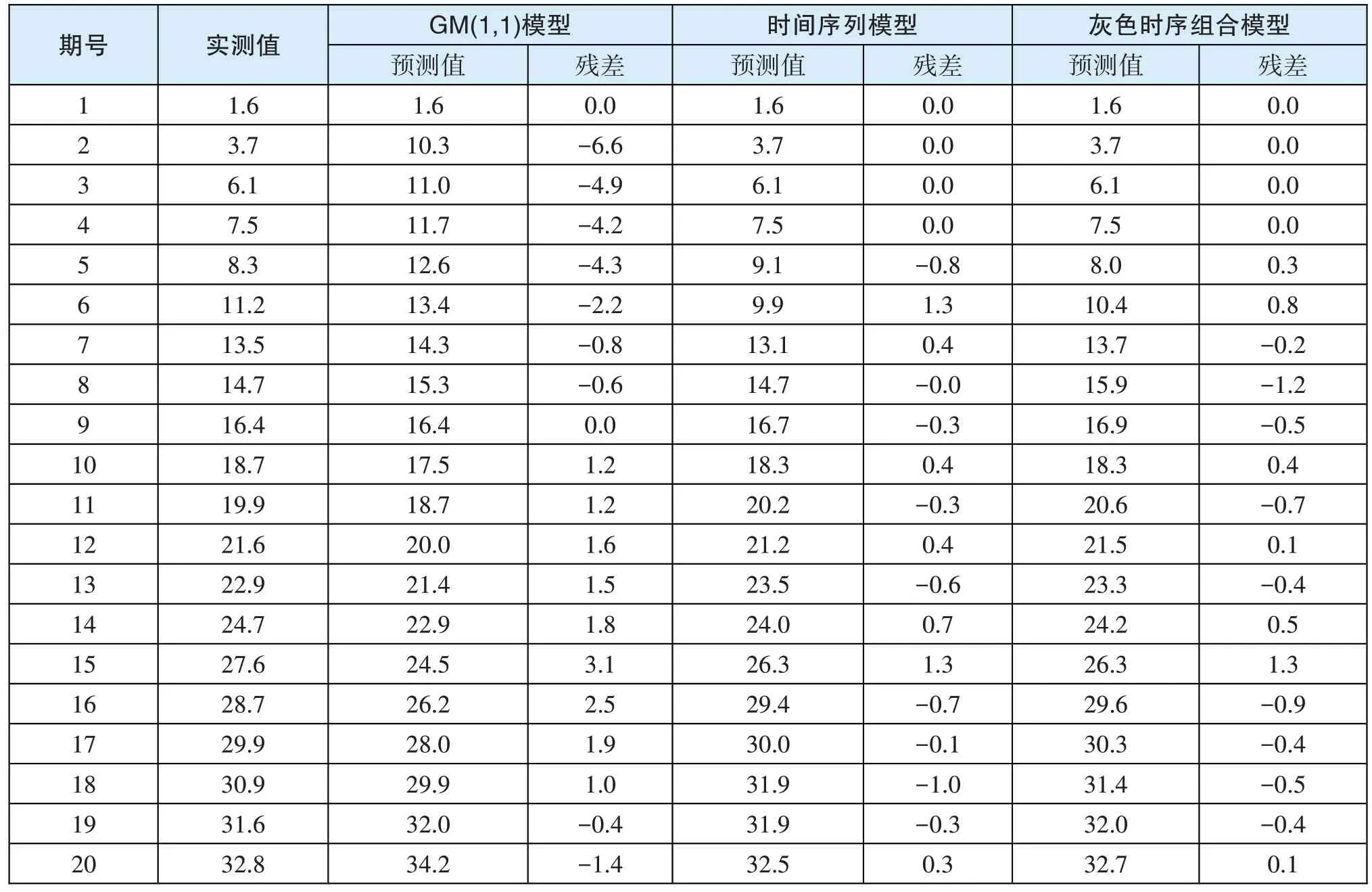
表2 20 期数据预测结果单位：mm

经过计算，3 种方法的评价精度分别为0.9640、0.9985 和0.9987，不难发现组合模型的精度最高，预测效果最好。

利用已建立的预测模型对后3 期数据进行预测，其结果分别如表3 和图2 所示。

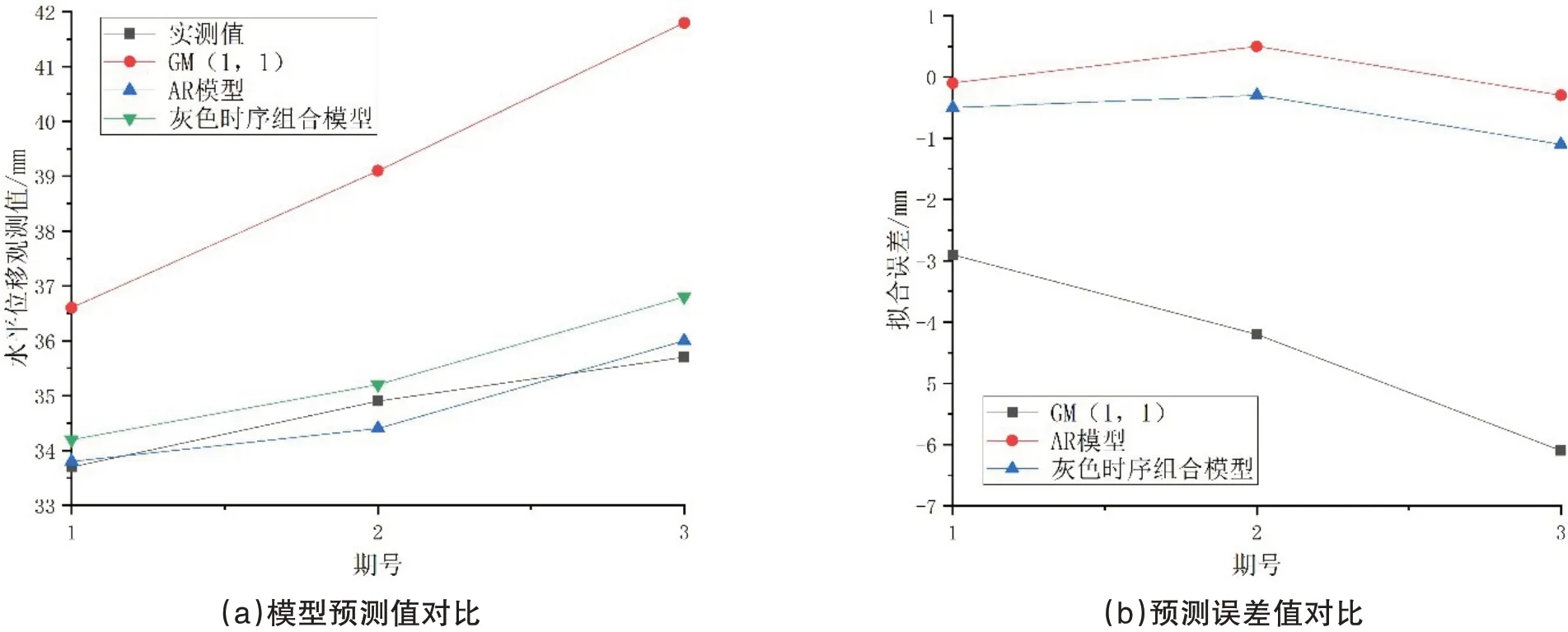
图2 模型预测结果

表3 3 期数据预测结果单位：mm

由图2、表3 可知：通过对后3 期数据进行预测检验，进一步证实组合模型预测效果为三者中最好的。

3 结语

基坑监测是基坑工程建设的基础，也是保障施工安全的关键环节，因此要对其加以重视并监测到位。本文对基坑监测所用的预测模型进行详细地阐述与多角度探究，通过具体工程实例，对不同预测模型进行了对比分析，得出组合模型能充分利用单一模型的优势，提高预测的可靠性。在对组合模型原理知识理解的过程中，通过结合工程实例分析组合模型预测效果得到了一些有效结论，仍然存在瑕疵，还需深入研讨：在实际工程中，不仅利用单一模型和组合模型来预测精度，还要研究在不同的工程中各类模型的适用范围以及优点和缺点；模型的适用范围是有限制的，当新数据加入后或者实际工程的影响使数据发生变化，则预测模型的精度会大大降低。所以应该结合实际情况，加入数据修正模型，以适应实际工程中各数据的变化，从而达到更好的预测结果。