双模式交通拥挤收费与按比例补贴联合策略设计
2023-02-04卢晓珊张雨斌骆明明
卢晓珊,张雨斌,骆明明,丁 恒
(1.合肥工业大学 汽车与交通工程学院,合肥 230009;2. 华南理工大学 土木与交通学院,广州 510641)
随着城市化的快速发展,居民出行需求也在迅猛增加。在有限的道路供给条件下,如何缓解道路交通压力成为众多城市关注的焦点问题。现有研究从拥挤收费、停车收费、可交易电子路票等方面提出了各种高峰期交通需求管理策略,或从公交服务、道路空间利用方面优化交通供给[1]。其中拥挤收费政策被视作一种有效的管理交通需求和优化出行结构的策略,归因于该政策调控的灵活性并且不产生额外运营成本。随着信息技术、全球定位系统的发展以及智能网联的普及,基于时空特征实施复杂定价政策具有了现实可靠性。深入研究城市多模式交通系统的协同收费机制对于缓解城市高峰通勤压力,促进不同出行模式间的协调具有重要意义。
在运用拥挤收费策略优化交通系统方面,学者们已开展了很多有意义的工作。Tabuchi[2]对比了公路不收费与统一收费对系统效率的影响,指出道路收费能降低汽车的使用率并改善公共交通收入水平;Arnott等[3]基于公路不收费与最优收费策略下的个人成本与系统效率提出了单阶段收费策略。结合收费政策的实际特性,Laih[4]在动态收费模型基础上进行改进,建立了阶梯收费模型。考虑阶梯收费中每阶段的末尾会产生用户堆积的情况,Lindsey[5]提出用于阶梯收费的“刹车模型”。
基于拥挤收费缓解高峰通勤压力的研究往往聚焦在小汽车出行的单一模式,小汽车以外的出行模式随后才被纳入研究。如基于经典的瓶颈模型,文献[2]首先研究了包含地铁和公路两种竞争方式的交通系统,但未考虑车厢拥挤和车辆之间的相互影响;Kraus[6]对双模式系统的公交定价以及容量设置的问题进行了深入讨论。以双模式交通均衡的研究为基础,考虑道路通行时间的随机性,Tian等[7]研究了出行者不确定性期望对出行方式划分和时间安排的影响。考虑不同出行方式之间的相互影响,Huang等[8]研究了小汽车与公交车共同造成的瓶颈拥堵,得到均衡状态下的出行方式划分模型;Li等[9]分析了公交相关的拥堵外部性对瓶颈系统的影响,发现在总社会成本方面,只对小汽车收费的策略优于同时向小汽车和公交车征收拥挤费。考虑时间价值的异质性,Zheng等[10]设计了基于异质用户时间价值的动态交通拥挤收费方案,指出将公交激励措施整合到收费方案中能有效地提高收费效率和公平性。目前针对公共交通补贴的研究一般倾向于单独考虑运营企业、乘客或政府的需求[11]。梁喜等[12]提出基于客流量的公交补贴优化模型;Drevs等[13]调查统计了公共交通补贴的效果和乘客支付的意愿,认为公共交通公司及融资机构应重视补贴,从而最大化发挥公共交通的服务价值。在政府管制和运营补贴两种条件下,Sun等[14]对比分析了公交运营表现,发现在政府管制和补贴的条件下,公交运营产生的社会福利最大,而在仅有补贴却缺乏管制的情况下社会福利最小。郭倩雯等[15]从公交运营方面提出了针对乘客的福利补贴与管理方式,基于票价、发车间隔等要素的分析得出提供补贴的最佳时机,从而兼顾社会和个人利益。公交补贴与拥挤收费之间存在一定的可交互性,值得统一考虑。Basso等[16]指出最佳拥挤收费与补贴的设计应联合考虑公交设计、时间成本和基建投资,证明了公交补贴与拥挤收费的联合机制有利于提高公众对于拥挤收费的接受度;徐淑贤等[17]考察了公交的边际成本定价和平均成本定价策略,建立均衡交通模型,发现当道路收费收入直接补贴给公交出行者时,从总出行成本上来看,平均成本定价策略优于边际成本定价。
综上,现有研究聚焦于拥挤收费策略的设计,往往适用于单一模式收费策略的优化,常假设拥挤收费的收入完全用以补贴公共交通。而收费与补贴的联合设计能让出行者认识到其对已拥挤的道路产生的边际成本时提高接受度,同时也能为交通管理者合理再分配拥挤收费的收入提供建议。因此,文中提出了三种不同的道路拥挤收费与地铁按比例补贴的联合策略,剖析其对双模式交通系统的出行方式划分和成本的影响,以推广拥挤收费策略与鼓励出行者向地铁转移,从而缓解城市高峰通勤压力、优化交通系统的结构。
1 模型描述
1.1 参数说明
文中涉及到的主要参数如下:
1.2 模型假设
研究场景为一条连接生活区(O)与工作区(D)的交通走廊,在连通生活区与工作区的道路上存在通行能力有限的瓶颈。通勤者可自驾或搭乘地铁到达工作地,模型假设如下:
不考虑道路通行时间的随机性;不考虑小汽车用户与地铁用户的时间价值的异质性;受通行能力限制,小汽车用户与地铁用户可能发生早到或晚到延误,一般认为γ2>β1>γ1,γ2>β2>γ1[18];不考虑出行者在站台的等待时间成本,其原因是高峰时段列车发车间隔很短,地铁用户在站台的等待成本很小,用户很难感知出发时间决策的等待损失,站台等待成本可被忽略[19]。
1.3 个人广义出行成本
文中构建的双模式交通系统如图1所示。地铁出行用户先步行距离l1到达起始地铁站口A,搭载地铁行进距离L到达终点地铁站口B后,再步行一段距离l2到达工作场所。小汽车用户从O点到D点的行驶距离为L+l,其中l=l1+l2。
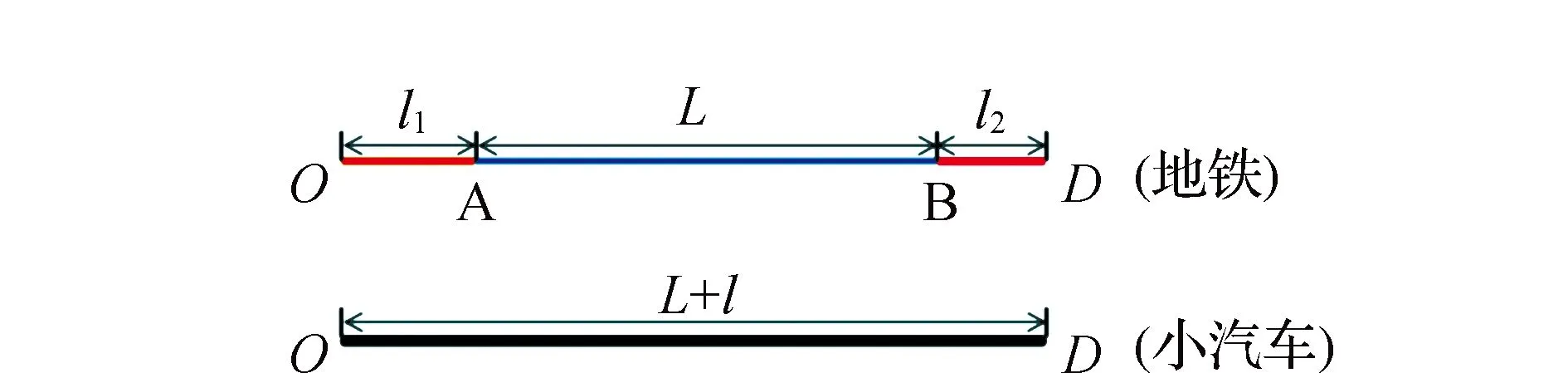
图1 双模式交通系统
小汽车用户的成本包括行驶时间成本、早到或晚到延误成本和固定成本。为简化运算,在不考虑道路随机延误时间的情况下,在时刻t出发的小汽车用户个人广义出行成本为:
CA(t)=
(1)
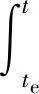
与自驾出行不同,搭乘地铁出行不会产生排队,但会产生与每一位乘客息息相关的拥挤成本,同时用户也必须支付对应的地铁票价。基于此,地铁用户的总出行成本包括步行时间成本和地铁行驶时间成本、早到或晚到延误成本、拥挤成本和地铁票价四部分,则在时刻t出发的地铁用户个人广义出行成本如下:
CT(t)=
(2)
式中:第1部分为步行时间成本和地铁行驶时间成本,用户的步行距离与平均速度分别为l与ν1,地铁行驶距离与平均速度分别为L与ν2;第2部分为乘客早到或晚到延误成本;第3部分为拥挤成本,m为单位时间车厢内个体乘客对其他乘客所产生的外部拥挤成本。根据文献[19]拥挤成本与列车行驶距离和车厢内人数两项因素成正比,假定在早高峰时段发出的列车数量为n,当n足够大时,第i+1列车次上的乘客数量能通过式(3)近似得到:
(3)
2 无收费补贴情形的方式选择均衡
2.1 小汽车用户均衡
根据用户均衡时所有小汽车用户无法通过改变自身出发时间使出行成本进一步降低,即所有小汽车用户的出行成本相同且为常数,出发率为:
(4)
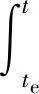
(5)

(6)
式中:δ=γ1γ2/(γ1+γ2)。
结合式(1),得到小汽车用户均衡出行成本如下:
(7)
2.2 地铁用户均衡
根据文献[20]的研究结果,te′、tl′时刻地铁用户的出发率为零,即R(te′)=R(tl′)=0,根据用户均衡定义,存在:
(8)
由式(8)可知t时刻地铁用户出发率为:
(9)

γ1(t-te′)=γ2(tl′-t)
(10)
(11)
则地铁高峰期长度为:
(12)
将式(11)代入式(8),得到地铁用户的均衡出行成本:
(13)
达到出行方式间的选择均衡需满足以下条件:
(14)
影响均衡出行成本CA与CT的因素与变量NA、NT有关。当上述条件满足时,达到方式划分的总体均衡,否则出行者仍会有更改方式选择的冲动。联立式(7)、式(13)和式(14),得到均衡时选择地铁和自驾的人数分别为:
(15)

3 不同收费补贴策略的方式选择均衡
3.1 道路统一收费+地铁按比例补贴(策略Ⅰ)
统一收费的费用应根据实际情况确定,收费费用确定后所有在该道路上通行的小汽车用户都应缴纳相应的固定费用。假设对每位小汽车用户统一征收费用为c,则拥挤收费的收入为cNA,该收入可部分用作道路维护和基础设施建设。考虑将总收入的1/ε(ε≥1)用于补贴地铁。在达到均衡状态时式(16)成立:
(16)
整理上述方程组,可得:
(17)
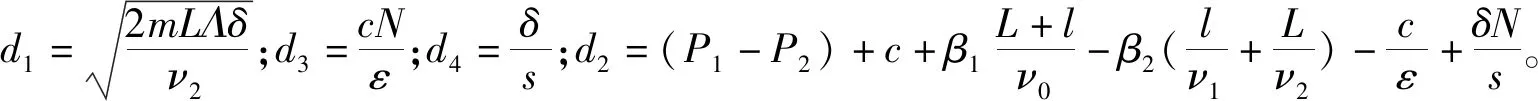
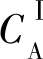
3.2 最优收费+地铁按比例补贴(策略Ⅱ)

(18)
整理式(18)可得:
(19)


3.3 阶梯收费+地铁按比例补贴(策略Ⅲ)

(20)
同理,简化后可得一元四次方程:
(21)
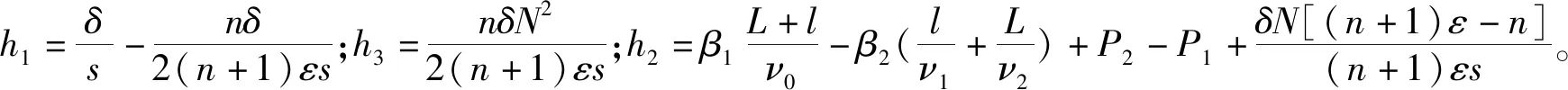
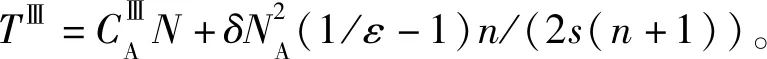
4 数值算例
本节通过数值算例分析不同策略对出行方式划分和社会总成本的影响,对关键参数进行敏感性分析。与参考文献[18]采用的算例类似,小汽车用户的固定费用、地铁用户的票价等取值不宜太大,避免对正常行驶时间成本、早到或晚到延误成本和排队等待时间成本等费用主体产生较大的影响。模型参数设置如下:N=8 000 人、s=1 000 pcu·h-1、P1=5 元、P2=2 元、β1=14 元·h-1、β2=14 元·h-1、γ1=4 元·h-1、γ2=20 元·h-1、ν0=60 km·h-1、ν1=4 km·h-1、ν2=80 km·h-1、L=30 km、l=1.5 km、m=0.25、Λ=0.1 h。
4.1 不同道路收费策略对方式划分的影响
4种方案(无补贴)下两类出行用户数量如表1所示。统一收费策略时部分小汽车用户转向地铁方式,用户均衡成本上升;最优收费和阶梯收费并未改变小汽车与地铁用户的出行成本,因此方式划分与不收费时相同。
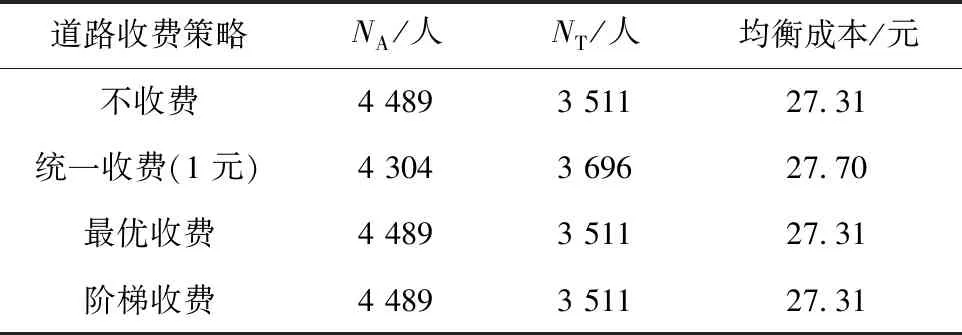
表1 不同收费策略下的出行方式划分
4.2 不同收费与按比例补贴策略对方式划分影响

图2 不同收费补贴策略下用户数量的变化
采用道路统一收费与地铁按比例补贴策略时地铁用户数量的变化如图2(a)所示。随着道路上小汽车用户被收取的费用增加,或对地铁的补贴比例的提高,小汽车用户向地铁方式转移的数量增加。采用道路最优收费与地铁按比例补贴策略时地铁和小汽车两类用户数量的相对变化如图2(b)所示。随补贴比例增加时,最优收费与地铁按比例补贴策略中用户的变化幅度比统一收费与地铁按比例补贴策略的大,如图2(b)和图2(c)。但值得注意的是,统一收费制度下地铁用户的初始数量比最优收费制度高,即统一收费初期会有更多小汽车用户选择地铁出行。阶梯收费与地铁按比例补贴策略下地铁用户数量的变化如图2(c)所示。当补贴比例固定时,阶梯收费划分的阶段越多,所获收益越多,每位地铁用户所获补贴也越多,因此地铁用户数量的增幅越大。
不同收费补贴政策对社会总成本和个人出行成本的影响如图3所示。随着补贴比例的提高,个人出行成本在各收费策略下皆呈下降趋势;但社会总成本的变化趋势因策略而异。实施阶梯收费和最优收费时,社会总成本随着补贴比例的提高而增加,但统一收费时的社会总成本变化趋势相反。由于道路排队在前两种收费策略中已被不同程度消减,社会总成本已达到最低,随着补贴比例的提高,道路收费的获利减少,导致社会总成本增加。此外,综合考虑个人出行成本和社会总成本,道路收费应优先采取最优收费,其次是阶梯收费和统一收费。

图3 不同收费补贴策略下的成本
4.3 参数敏感性分析
上节对双模式交通系统收费策略的分析是基于宏观层面的,本节对影响交通方式划分的重要运营参数进行敏感性分析,分析发车间隔、地铁票价和道路通行能力变化对个人均衡成本、方式划分以及高峰期长度的影响。由于在无补贴的情况下,最优收费与阶梯收费策略下的方式划分与不收费时相同(见表1),故下述分析以不收费为例进行讨论。
4.3.1 发车间隔的影响
不同发车间隔Λ的影响结果如表2所示。当发车间隔缩短时,地铁用户数量增幅较大,小汽车用户大幅度减少,缩短了道路高峰期长度。同时,由于随着发车间隔缩短,单次列车上所载乘客减少,拥挤成本降低,个人均衡成本降低。由式(12)可知地铁的高峰期长度受发车间隔和用户数量的双重影响,但是地铁用户数量对于高峰期的延长效果不如发车间隔对高峰期的缩短效果明显,因此地铁高峰期总体缩短。

表2 不同发车间隔Λ的影响结果
4.3.2 地铁票价的影响
不同地铁票价P2的影响结果如表3所示。当地铁票价降低时,地铁用户数量小幅增加,小汽车用户数量减少,均衡费用降低;道路高峰期长度会随用户的减少而缩短,而地铁高峰期长度随地铁用户数量的增加而延长。比较表2与表3中小汽车和地铁用户数量的变化幅度以及高峰期长度的变化趋势,地铁发车间隔对于整体的影响大于地铁票价对于整体的影响。

表3 不同地铁票价P2的影响结果
4.3.3 道路通行能力的影响
不同道路通行能力s的影响结果如表4所示。当道路通行能力下降时(如道路养护或维修时需要封闭部分车道或恶劣天气等原因),个人均衡成本增加,小汽车用户减少,地铁用户增多且增幅较大。地铁高峰期长度随着地铁用户的增加而延长,而小汽车用户数量减少对高峰期长度的缩短效果不如通行能力降低对高峰期长度的延长效果明显,因此道路高峰期总体延长。

表4 不同道路通行能力s的影响结果
5 结 论
以往的研究只考虑了一种收费策略或完全补贴的情形,本研究提供了双模式的统一研究框架,可根据不同的收费方式需要加以应用。基于此,文中研究分析了3种道路拥挤收费与地铁按比例补贴的联合策略对双模式交通系统的出行方式划分和成本的影响,并进一步探究地铁发车间隔、地铁票价水平、道路通行能力等关键因素对出行选择的影响,得出如下结论:
1)对比3种策略,采用统一收费策略时地铁用户的初始增长量最高,即实施统一收费初期有更多小汽车用户选择地铁出行,但在补贴时增长幅度不及其他收费策略,且社会总成本最高,因此统一收费适合作为短时调节措施。考虑阶梯收费易于实现,对于地铁用户数量与社会总成本的影响效果与最优收费差别不大,且低于统一收费,因此阶梯收费适合作为长期调节措施。
2)随着补贴地铁比例的增加,地铁用户的数量明显增加,政府可通过提高对地铁的补贴力度以吸引更多的乘客。实施统一收费策略时增加补贴力度,对个体和社会整体都有利,但在最优收费和阶梯收费策略下,补贴比例的提高仅对个体有利,对社会总成本不利,即地铁补贴比例并非越多越好,管理者在收费政策制定中可以权衡决定。
3)缩短发车间隔和降低地铁票价皆能吸引更多的地铁乘客,但地铁用户数量与个人出行成本对发车间隔更敏感,即缩短发车间隔对于系统整体提升效果优于降低地铁票价的措施。
