单井抽出-回渗同步循环地下水水力控制模型研究

2023-02-04王新港徐祥健姜永海

环境科学研究 2023年1期

王新港，杨昱，徐祥健，韩旭，夏甫，邓圣，肖瀚*，姜永海

1. 中国环境科学研究院，国家环境保护地下水污染模拟与控制重点实验室，北京 100012

2. 河北工程大学能源与环境工程学院，河北邯郸 056038

单井抽出-回渗同步循环地下水水力控制技术是从地下水污染羽范围内采用单井抽出污染地下水，经过处理后，在抽水井周边同步等量回渗至包气带和含水层，通过抽出-回渗同步循环，人为改变污染羽及其周边区域地下水流场和水力梯度，将受污染的地下水控制在一定范围内，防止污染物进一步扩散蔓延，进而将受污染的地下水体与未受污染的清洁地下水体分隔开，是地下水污染修复的重要手段[1-5]. 该技术的优势是操作简单、运行成本较低、加速地下水循环流动缩短地下水修复时间，影响该技术实施效果的重要因素是水动力条件以及含水层水文地质条件，水动力条件主要由抽注水量控制，而含水层水文地质条件主要指含水层渗透性[6-13].

在地下水污染水力控制技术领域内，已有研究主要关注抽注技术参数的选取以及抽注水井布局和抽注水量的优化对水力控制效果的影响，使抽注井的布局和抽注水量更为合理，从而缩短抽注时间、提高水力控制效率[14-19]. 如Bear等[20]定量地研究了注水井补给对含水层地下水运动规律的影响，为水力控制技术的发展奠定了理论基础；Shar等[21]、Christ等[22]采用解析、半解析法分别研究了相同流量下任意双抽水井及不同流量下多抽水井水力控制区域的边界形态特征，为数值模拟提供了理论基础；随后，Wang等[23]用数值模拟和优化耦合方法，采用拉普拉斯变换有限单元法对均匀等厚污染含水层的多个抽注井进行位置布设，提高了捕获污染的有效性；Matott等[24]采用分析单元法对井群系统的抽水井数量、位置和抽水量进行了优化；刘苑[25]和万鹏[26]均采用MGO模块结合遗传算法对水力控制系统进行优化，通过约束抽水井数量、抽水流量、水头和抽水总量等参数，提高了水力控制能力. 目前地下水污染水力控制技术研究中数值模拟成为主要解决手段，常用的数值模拟软件主要包括Groundwater Modeling Systems(GMS)、Visual MODFLOW、FEFLOW及Groundwater Vistas等[27-28]. 然而单井抽出-回渗技术特点是抽出-回渗循环同步进行，通过人工干扰/控制实现水力控制下抽出-回渗同步进行的研究相对较少[29].

研究采取物理模型和数值模型相结合的方法，搭建实验室尺度砂柱孔隙含水层物理模型，基于该物理模型构建MODFLOW地下水流数值模型并校准，使模拟地下水流可以较好地刻画实际地下水流；利用校准后的数值模型模拟不同抽注水量和含水层渗透性条件下实现水力控制时不同位置地下水水位的差异，基于潜水完整井稳定流公式-裘布依公式的数据拟合，分析实现水力控制时含水层不同位置水位与抽注水量和含水层渗透系数的关系以及回渗半径对水力控制的影响. 该研究论证了单井抽出-回渗同步循环地下水水力控制技术实现人工控制地下水流场和水力梯度的可行性，并量化了水动力条件和水文地质条件的影响，以期为该技术在实际场地的应用提供重要参考.

1 材料与方法

1.1 物理模型

1.1.1装置搭建

单井抽出-回渗同步循环地下水水力控制技术试验装置如图1所示. 试验装置由砂柱、布设于砂柱中轴线的抽水管、砂柱表层的布水管以及砂柱含水层内部不同位置、不同深度的测压管组成.

图1 单井抽出-回渗同步循环地下水水力控制技术试验装置Fig.1 Schematic diagram of single well pumpingrecharge synchronous cyclical groundwater hydraulic control technique device

砂柱由1 cm厚有机玻璃制成，直径为100 cm，高度为100 cm. 砂柱内均匀填充石英砂〔采购于天津某石料厂的80～120目(100目=0.150 mm)石英砂〕，通过下部进水且每5 cm进行饱和夯实的方式装填，构建厚度为70 cm的均质潜水含水层. 抽水管(长100 cm、直径2 cm、开筛70 cm)垂直固定于砂柱中轴线位置并包裹160目过滤筛网防止石英砂进入，管底位于砂柱底部(用于模拟抽水完整井)，管顶与蠕动泵相连接. 布水管以抽水管为圆心，半径32 cm范围内螺旋状均匀铺设于砂层表面(布水管内径0.6 cm，每隔5 cm开孔)，一端与蠕动泵相连接，使抽出的水等量同步均匀回渗至砂柱含水层中. 蠕动泵型号为保定兰格BT100-1L，泵头为YII25，可调整流量范围为0.1～180 mL/min.

1.1.2测试方法

装置监测点位如图2所示，采用上密下疏、内密外疏的方式，通过砂柱侧面48个监测孔在砂柱内不同位置、不同深度安装48个测压管，用于监测含水层水位. 垂向共8层，测压深度分别为1、3、5、7、14、28、48、70 cm，每层设置6个测压点，分别与中心抽水井井轴相距2、4、8、14、22、32 cm. 测压管读数实时反映砂柱内不同位置、不同深度含水层水位的变化. 砂柱物理模型的渗透系数和孔隙度分别由抽水试验、补水试验测算[30]. 抽水试验测定渗透系数的原理是基于潜水完整井稳定流公式-裘布依公式[31]：

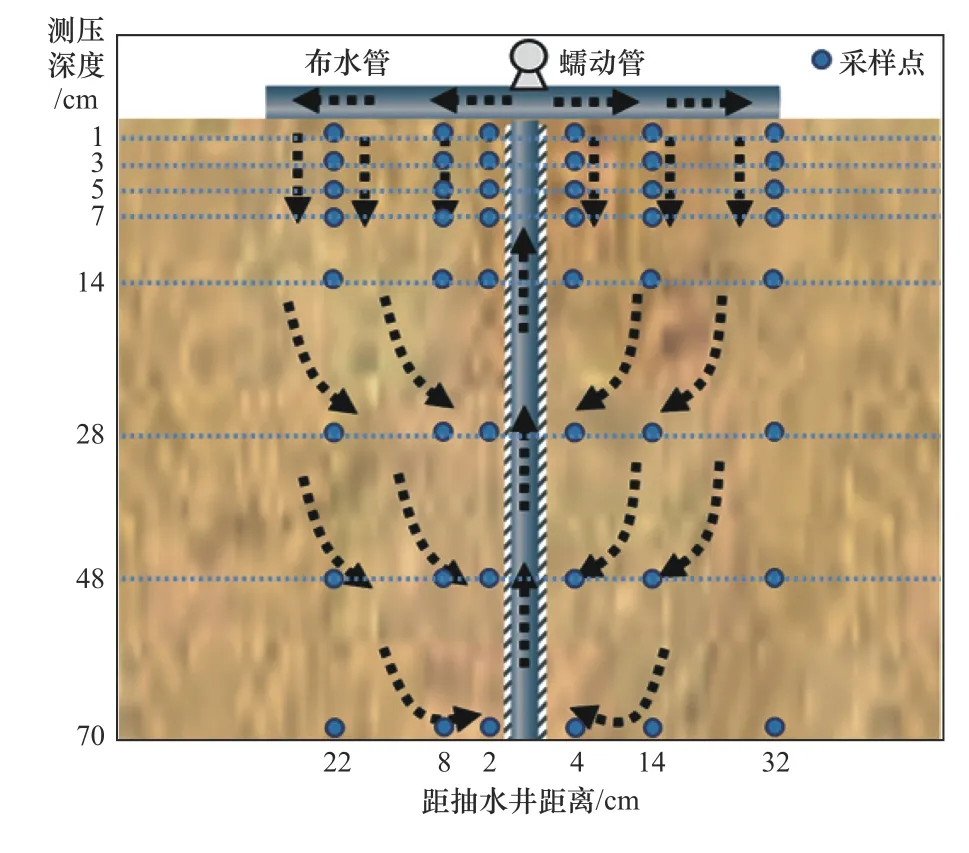
图2 单井抽出-回渗同步循环地下水水力控制技术试验装置概念Fig.2 Conceptual diagram of single well pumpingrecharge synchronous cyclical groundwater hydraulic control technique device

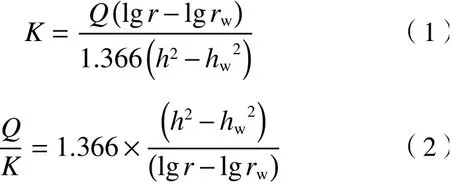
式中：Q为抽水井流量，m3/d；K为含水层渗透系数，m/d；h为含水层中任意位置地下水水位，m；hw为抽水井水位，m；r为含水层中某处与抽水井井轴距离，m；rw为抽水井半径，m.

实验室尺度砂柱物理模型搭建完成后，给定抽水量为2.5 cm3/s，运行开展抽水试验，获取抽水稳定后不同位置、不同深度观测水位，计算得到砂柱模型填土的渗透系数为0.01 cm/s，孔隙度为0.4.

1.2 数值模型

1.2.1模拟软件选取

GMS是一个界面友好、处理功能强大的地下水数值模拟软件[28,32]. MODFLOW模块离散方法简单、求解方式多样、采用了模块化结构，广泛应用于地下水渗流和溶质运移[33]. 该研究采用GMS中的MODFLOW模块构建实验室尺度砂柱孔隙含水层三维地下水稳定流模型. MODFLOW模块的水流控制方程[31]如下：

式中：W为水流源汇项，m3/d；t为模拟预测的时间，d；h为地下水水位值，m；μs为含水层储水率，m-1；Kx、Ky、Kz为不同轴向上的渗透系数值，m/d.

1.2.2模型构建

数值模型参照上述物理模型等比例构建，模拟单井抽出-回渗循环过程含水层流场，4种模型构建参数条件如表1所示. 模拟区域为试验砂柱的石英砂填装区(直径100 cm、高度70 cm)，水平方向剖分为1 cm ×1 cm的正方形网格(100行、100列)，垂向剖分为4层，从上至下各层厚度分别为20、16、24、10 cm.

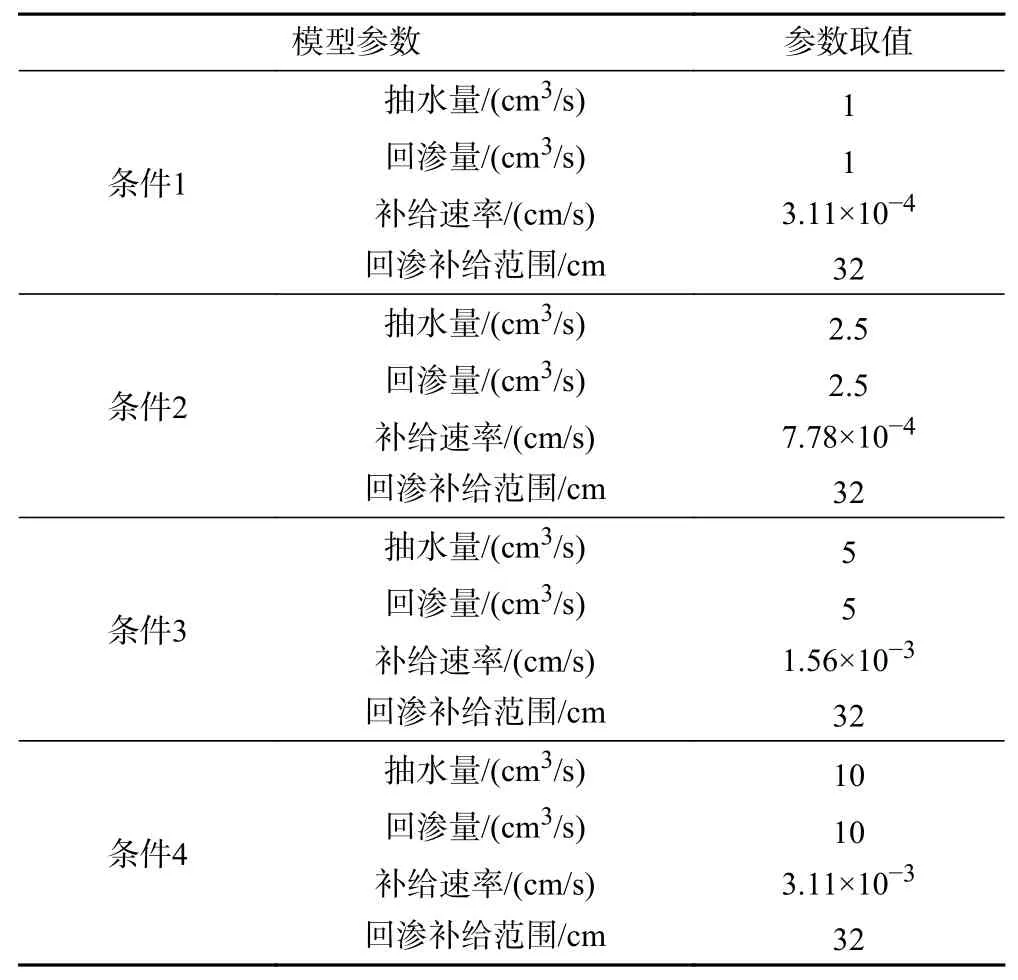
表1 模型构建参数Table 1 Parameters for model construction

模拟区域下部及侧向边界设定为零流量边界；模拟区域中心有抽水井排泄，设定为定流量边界(抽水量分别设定为1、2.5、5、10 cm3/s)；模拟区域上部边界有回渗补给(补给范围为以抽水井井轴为圆心，半径32 cm的圆)，设定为定流量边界(回渗量分别设定为1、2.5、5、10 cm3/s，对应的补给速率分别为3.11×10-4、7.78×10-4、1.56×10-3、3.11×10-3cm/s).

1.3 数值模型校准

为保证模型模拟结果可靠，对模型进行校准验证. 物理模型的48个观测点分别在抽出-回渗量为1、2.5、5、10 cm3/s达到抽出-回渗平衡时记录实测水位，对比抽出-回渗量分别为1、2.5、5、10 cm3/s时数值模型的模拟水位与物理模型的实测水位，微调渗透系数，重复多次试算，直至大部分观测点模拟水位与实测水位的误差达到模拟精度要求.

数值模拟结果的准确度通过纳什效率系数(Nash-Sutcliffe efficiency coefficient, NSE)验证[34].

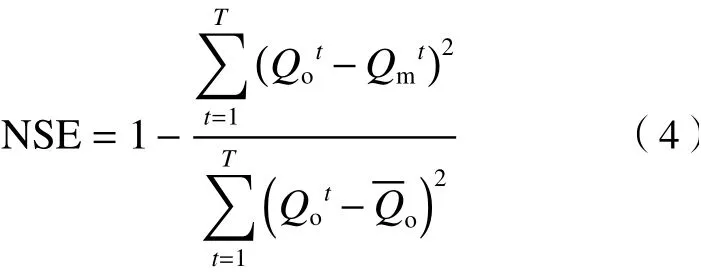
式中：Qo为实测水位值，cm；Qm为模拟水位值，cm；为t时的实测水位值，为实测水位值的总平均值，cm.

NSE取值为负无穷至1，NSE接近1，表示模型质量好，模型可信度高；NSE接近0，表示模拟结果接近观测值的平均值水平，即总体结果可信，但误差大；NSE远远小于0，则模型不可信.

数值模型校准后，渗透系数调整为0.005 cm/s，模拟水位和实测水位(见表2)分散比较结果如图3所示，纳什效率系数达到0.88，说明模型精度较为理想，可以较好地刻画物理模型中的实际地下水流场.

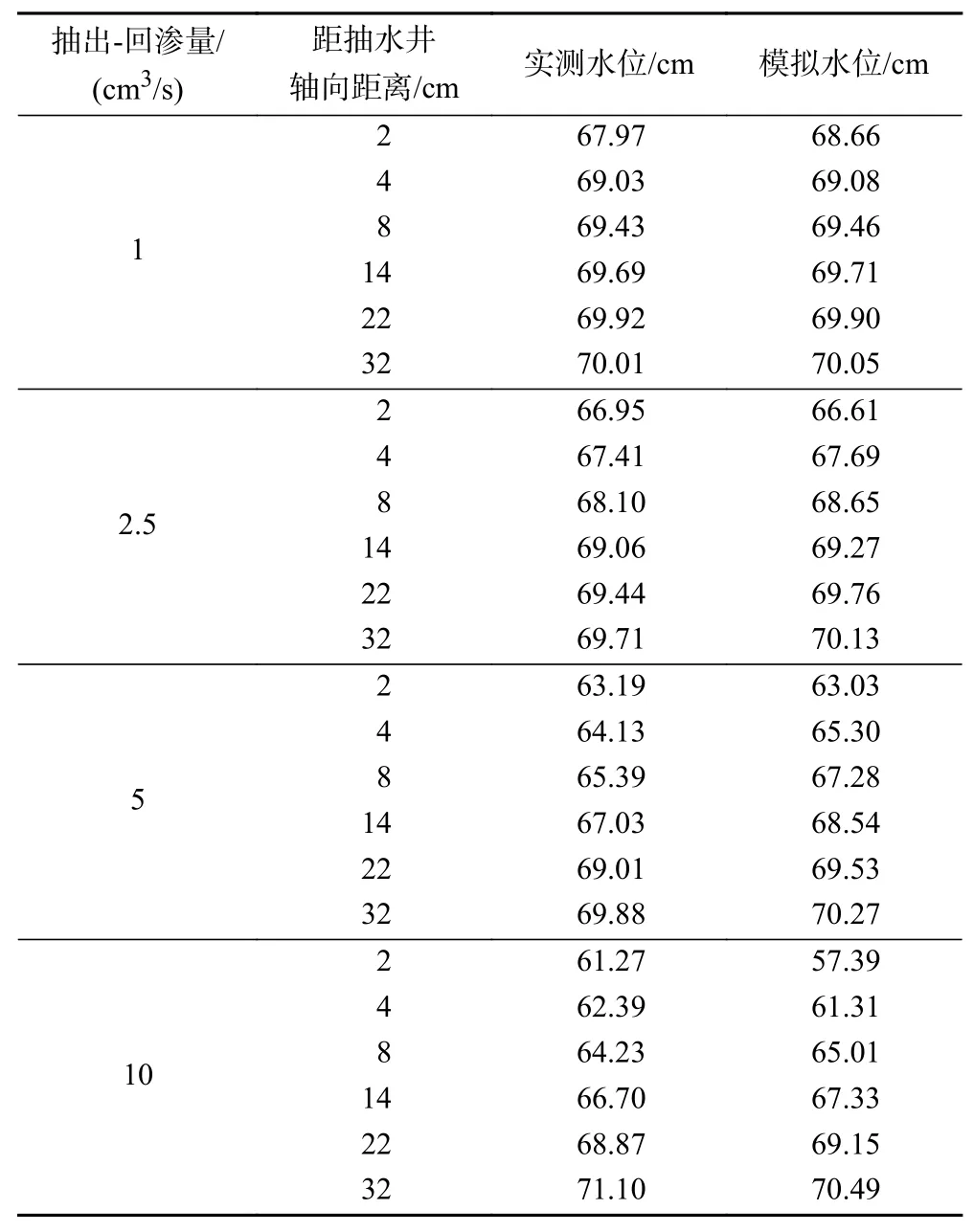
表2 不同抽出-回渗量条件下模拟水位和实测水位对比Table 2 Comparison between simulated and observed groundwater levels under different pumping-return seepage conditions

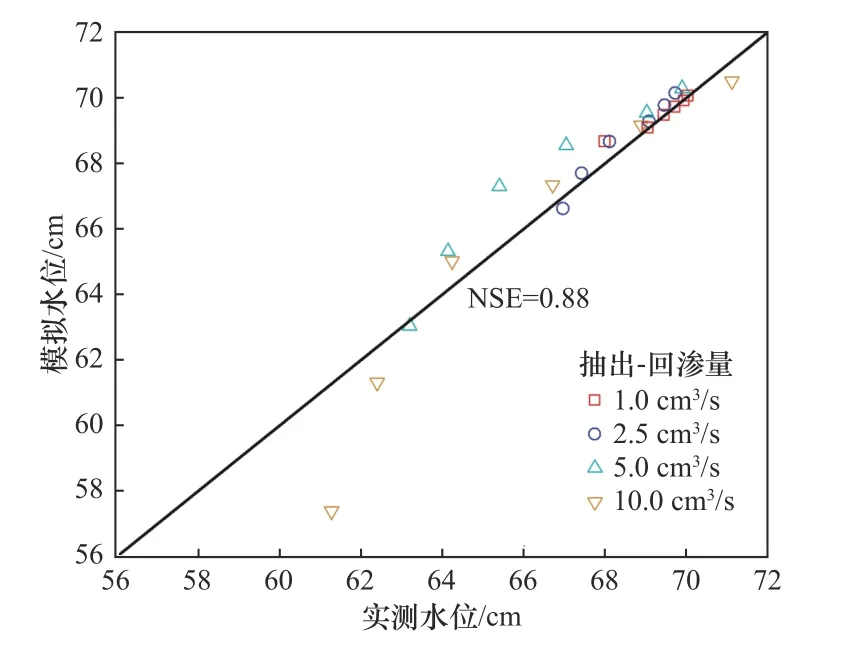
图3 不同抽出-回渗量条件下模拟水位和实测水位的分散比较Fig.3 Comparison diagram between simulated and observed groundwater levels under different pumping-return seepage conditions

2 结果与分析

2.1 实现水力控制时的模拟流场

当抽出-回渗量分别为1、2.5、5、10 cm3/s时，达到抽出-回渗平衡后，模拟流场三维空间分布如图4所示；距离抽水井轴0、2、4、8、14、22、32 cm处的模拟水位以及抽水影响半径见表3. 抽出-回渗量对水位降落漏斗的深度影响较大，抽出-回渗量越大，降落漏斗的深度越大. 当抽出-回渗量分别为1、2.5、5、10 cm3/s时，最大降深分别达到1.76、4.55、9.75、18.65 cm，分别为含水层厚度的2.5%、6.5%、13.9%、26.6%. 然而，抽出-回渗量对水位降落漏斗的范围几乎无影响，抽水影响半径几乎不随抽出-回渗量的变化而变化.

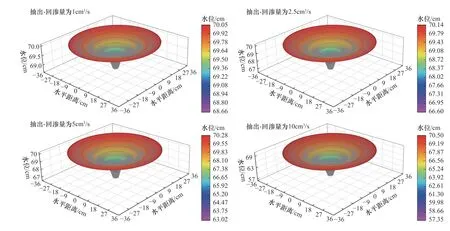
图4 不同抽出-回渗量条件下模拟流场三维空间分布特征Fig.4 Characteristics of simulated three-dimensional spatial distribution of the flow field under different pumping-return seepage conditions

表3 不同抽出-回渗量条件下模拟水位及抽水影响半径Table 3 Simulated water level and pumping influence radius under different pumping-return seepage conditions

2.2 实现水力控制时水位与抽注水量和含水层渗透性的关系

已有研究[6]表明，实现水力控制时含水层不同位置处的水位h主要取决于抽出-回渗量Q(水动力条件)和含水层渗透系数K(水文地质条件). 基于抽出-回渗量和含水层渗透性设置不同情景，利用校准后的数值模型模拟不同情景实现水力控制时地下水水位的分布特征，采用潜水完整井稳定流公式-裘布依公式开展数据分析拟合，分析实现水力控制时含水层不同位置水位与抽注水量和含水层渗透系数的关系，获取单井抽出-回渗同步循环地下水水力控制技术关键参数之间的定量关系.

选取《工程地质手册》提供的不同岩土类型(细砂、中砂、粗砂、砾砂)渗透系数的经验值[35]设定4种水文地质条件情景，选取不同抽出-回渗量(1、2.5、5、10 cm3/s)设定4种水动力条件情景，共计16种组合情景(见表4).

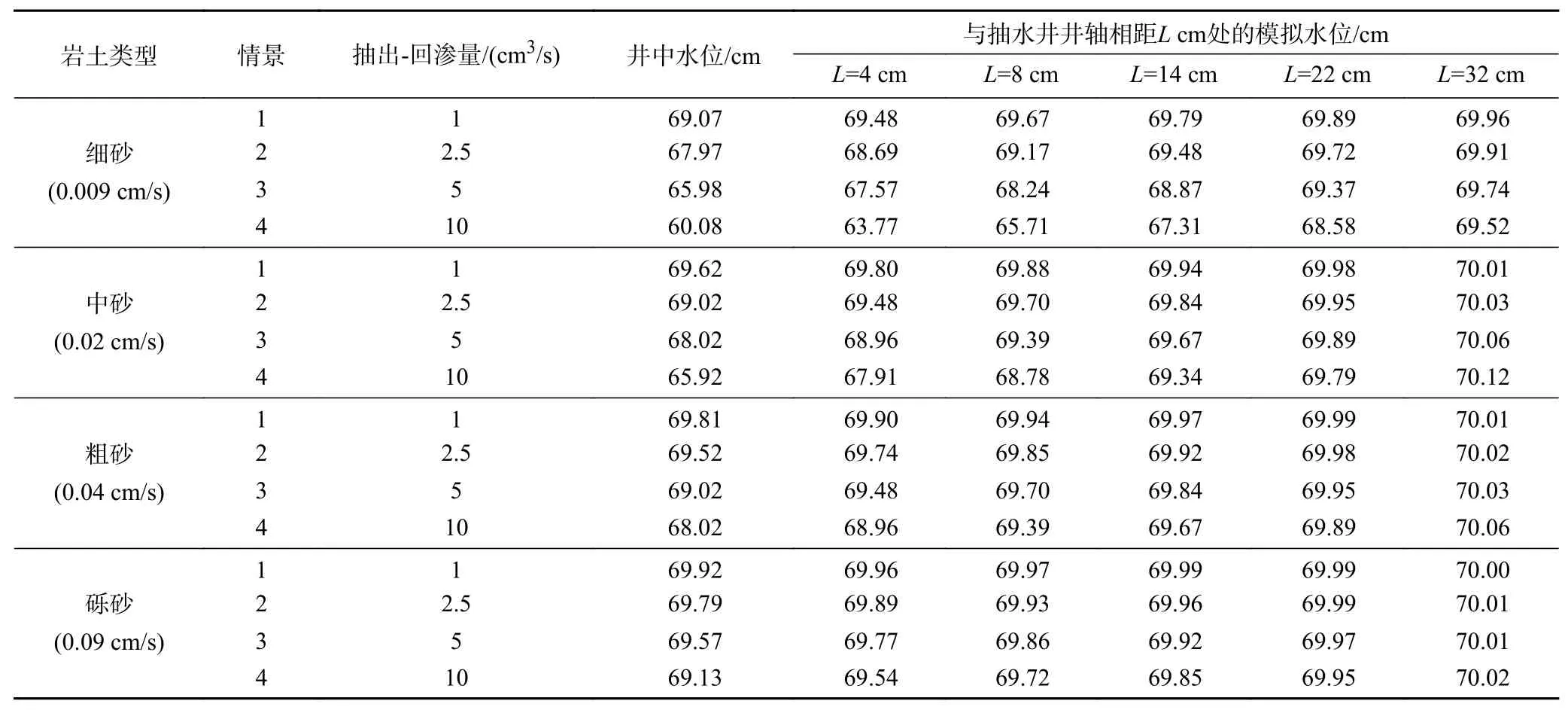
表4 不同情景水位模拟结果Table 4 Simulation results of water level under different scenarios

基于裘布依公式，对16种组合情景模拟得到的抽水井处水位以及距抽水井井轴4、8、14、22、32 cm处的模拟水位进行数据分析拟合，获取Q/K与(h2-hw2)/(lgr-lgrw)之间的定量关系(见图5)和拟合方程〔见式(5)〕. 由图5可见，Q/K与(h2-hw2)/(lgr-lgrw)之间呈线性关系，拟合系数(R2)达到0.99. 拟合后得到的线性方程斜率(α)为154.84～197.85，远大于式(2)中的斜率(1.366)，主要是因为裘布依公式的适用条件是补给项仅为侧向渗流补给，不含上层回渗补给，而单井抽出-回渗同步循环地下水水力控制技术在抽水的同时从上层同步等量回渗补水，导致砂柱边界地下水水位明显高于中部地下水水位，水力梯度明显增大.

图5 16种情景下模拟水位的数据分析拟合结果Fig.5 Simulated groundwater levels analyses and fitting results under 16 various scenarios

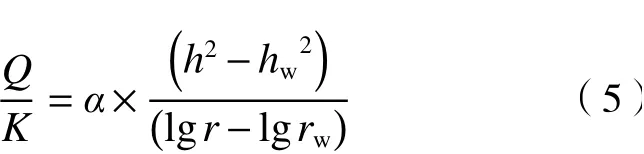
拟合方程(5)的斜率区间为154.84～197.85，存在一定程度波动，为探究斜率波动原因，基于表4设置的不同情景和现有模拟结果分析，利用校准后的数值模型模拟不同回渗半径下实现水力控制时拟合方程(5)的斜率变化. 目前回渗半径为32 cm，进一步考虑回渗半径为15、20、25、30、35、40、45、50 cm 8种情况，在此基础上对16种组合情景模拟得到的抽水井处水位以及距井轴4、8、14、22、32 cm处的模拟水位进行数据分析拟合，对式(5)中的斜率进行校正，结果如表5所示. 由表5可见，回渗半径与斜率之间存在一定关系，且拟合度比较高，R2均达到0.99. 随着回渗半径增加，拟合后得到的线性方程斜率在一定范围内逐渐增大，且拟合方程呈明显的线性正相关关系；当回渗半径接近边界半径时斜率范围逐渐减小，其中回渗半径等于边界半径时，斜率范围为178.18～183.9，而回渗半径为15 cm时，斜率范围为164.99～206.34，范围较大；此外，当回渗半径固定时，随着监测点位距离的增加，方程斜率逐渐增加. 主要原因是对于不变的水文地质条件，当流量确定后，回渗半径大小不同，直接影响回渗范围内地下水水位的变化，因此合理地调整回渗范围大小，有利于实现水力控制.

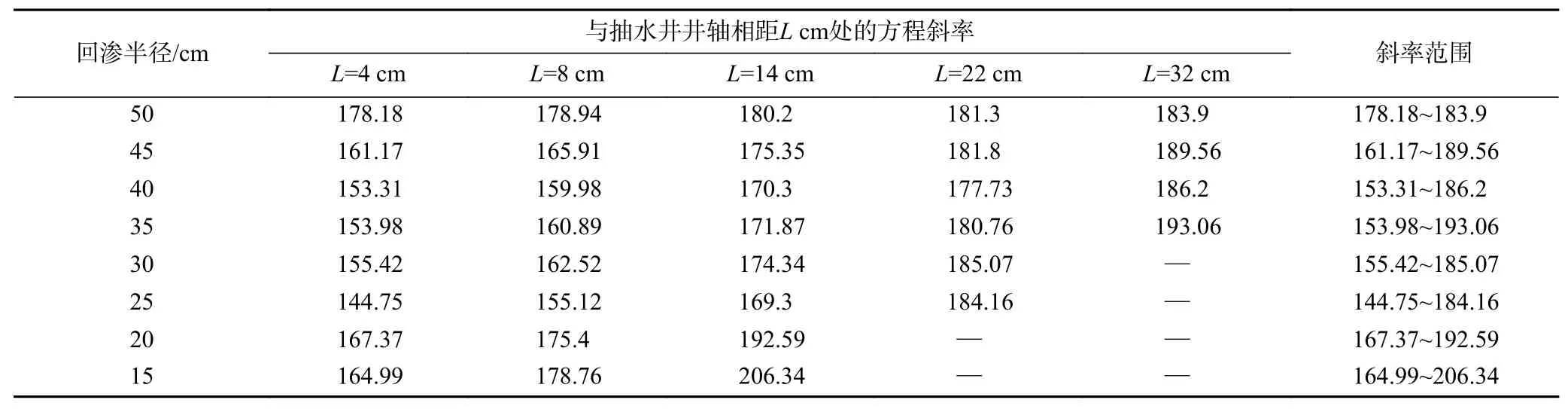
表5 16种情景下的方程斜率Table 5 Equation of the slope of equations under 16 various scenarios

3 讨论

通过单井-抽出回渗同步循环地下水水力控制技术的数值模拟结果，使用裘布依公式进行了拟合，对该问题中水动力参数、水文地质参数以及回渗范围进行了初步分析，得到了参数之间的对应关系，当回渗量取值为零时，方程中各参数之间变为经典裘布依公式中的参数关系. 对不同岩土类型均质含水层的模拟旨在概化不同类型渗透性场地中的参数关系.

在实际应用上，对场地回渗过程要求为均匀稳定入渗，然而自然场地一般为非均质性，入渗一般是不均匀、不稳定的，对该问题的较好解决方式仍是使用数值模拟，通过不同尺度下大量水动力条件和非均质的水文地质条件的组合，同时调整抽出-回渗量和回渗范围进行模拟研究，以此得出参数之间的进一步关系，使之更贴近于实际应用条件.