基于Fluent的棉花烘房流场均匀性优化*

钱睿，吴达科，杨明金

(西南大学工程技术学院，重庆市，400715)

0 引言

干燥是使农产品可长期保存的重要手段，在传统的气流上升式[1]热泵热风干燥工艺中，热泵将热空气通过管道送入烘房对农产品直接进行干燥，或进入烘房后穿过普通匀风板进行烘干，如此干燥过程结束后出现不同位置农产品干燥过度或干燥不足的情况，整体干燥品质较差，直接影响到农产品的后续储存。因此，对此类烘房进行结构优化势在必行。但在实际改进中，依靠经验在现场改变烘房结构的方法并不可靠，且会造成大量的资源浪费。利用计算流体力学软件模拟烘房内部气流流动情况可以准确暴露内部结构存在的“缺陷”，从而有针对性地进行优化改进，将大大减少人力物力消耗。

近些年来，CFD技术在喷雾干燥领域[2-5]、热风干燥领域[5-8]以及干燥参数优化[9-11]等方面应用发展迅速。国内外学者借助CFD技术对于农产品热泵烘房的结构优化进行了广泛深入的研究。Babu等[12]利用Fluent软件比较了四种不同托盘结构叶片干燥室的干燥性能，确定了最佳优化方案，大大提高了叶片干燥时的传热传质效率；王嘉麟等[13]针对固定床式花生荚果烘房设计了一种挡板组合式匀风机构，很好地改善了干燥均匀性问题；王振文等[14]利用Fluent提出在菊花烘房设置导流板可以使气流分布更加均匀；刘瑞等[15]提出在菊花热泵烘房进风口设置引风罩，借助于Fluent研究了引风罩最佳角度与长度，改善了整体空间的气流均匀性。上述研究针对不同农产品或不同类型烘房的优化均有一定效果，但目前对于气流上升式热泵烘房内部进行结构优化，以改善内部流场均匀性的研究少之又少。

本文针对已研发的通用型气流上升式热泵烘房存在的农产品干燥不均匀问题，利用CFD技术研究烘房空载与满载下的内部气流分布情况，探寻影响热空气分布的结构因素，设计9组不同角度的导流叶片与不同变方孔径匀风板的组合优化方案，探讨最佳组合方式，为后续实际干燥工艺改进提供技术参考。

1 烘房建模及模拟方法

1.1 三维模型建立及网格划分

本文所用热泵是以热泵烘干双机V102-X为原型，主要由热泵供热系统、温控系统、烘房热风循环系统等组成。烘房主要由底部匀风区域、物料干燥区域、回风区域组成。热空气所需热量由空气源热泵及辅助电加热产生。具体烘房尺寸参数如表1所示。

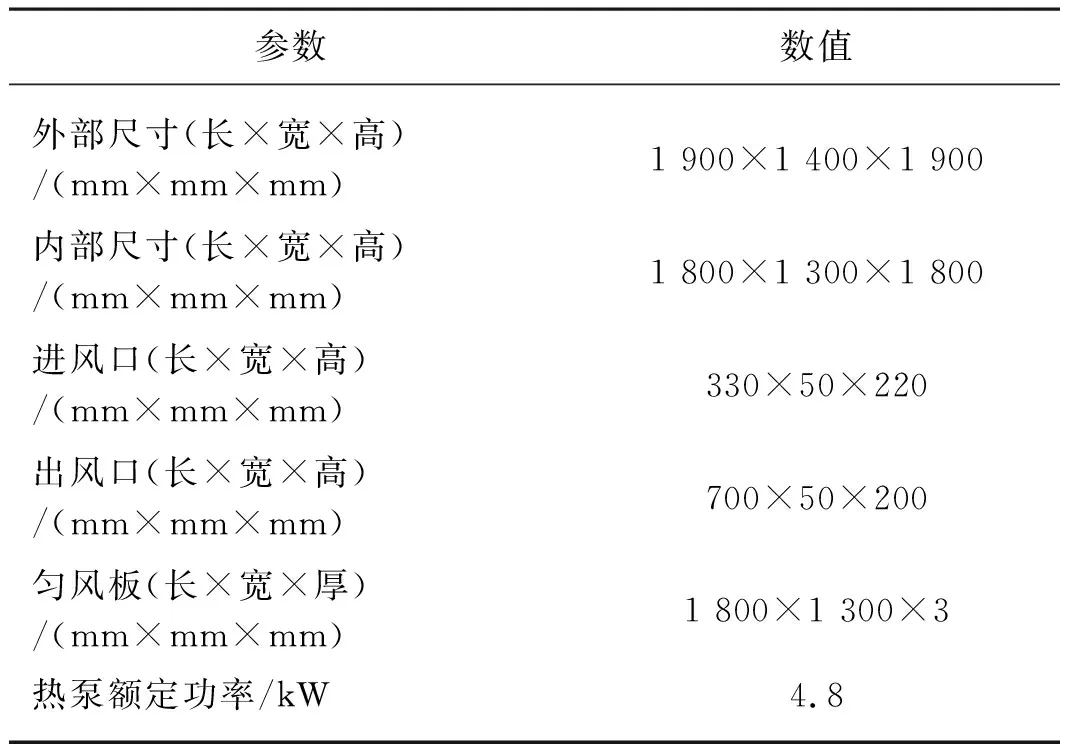
表1 烘房主要参数Tab. 1 Drying room size parameters

此空气源热泵干燥的完整过程是：空气在热泵系统中经过冷凝器被加热，通过管道进入烘房对物料进行干燥，热空气带走物料中的水分，再通过回风口返回热泵系统进行除湿加热，如此循环。利用Solidworks所建立烘房模型以及在ICEM中网格划分如图1所示。

(a) 空载烘房三维图 (b) 空载烘房网格

本文以棉花作为待烘干物料，由于实际烘房采用的是整体烘干，因此满载时将棉花层设置为多孔介质区域，具体尺寸为1 620 mm×1 080 mm×1 267 mm。

1.2 基本假设

1) 烘房材料具有良好的保温效果以及绝热性能，可看作对外热损较少，视为绝热。

2) 实际干燥过程，流体包含空气与水蒸气两种物态，但由于本文重点研究烘房内流场的分布，所以将流体看作干热空气。

3) 热空气在烘房内流动时，压强与温度变化小，密度变化很小，因此可视热空气为不可压缩流体[16]。

1.3 数学模型

1.3.1 湍流模型

不可压缩流体的流动满足质量守恒方程以及动量守恒方程。湍流模型选择标准k-ε模型，此模型即在湍动能k方程的基础上，加入一个湍动耗散率ε的方程，形成k-ε双方程模型[17]。

Gb-ρε-YM+Sk

(1)

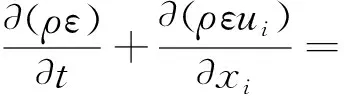
(2)

(3)

(4)

(5)

式中：μt——普朗特假定湍动粘度；

μ——流体动力粘性系数，取值为1.789 4×10-5；

ui、uj——湍流速度在第i、j个方向上的分量；

Gk——平均速度梯度引起的湍动能产生；

Gb——浮力影响引起的湍动能产生；

YM——过渡的扩散所产生的波动，对于不可压缩流体YM=0；

Sk、Sε——用户自定义源项；

C1ε、C2ε、C3ε——经验常数，Fluent中默认取1.44、1.922、0.09；

σk、σε——湍动能和湍动耗散率对应的普朗特数，Fluent默认取1.0、1.3；

gi——重力加速度在第i个方向上的分量；

Prt——湍动普朗特数，默认取0.85；

Cμ——经验常数；

T——流体温度；

β——热膨胀系数；

ρ——流体密度，取1.225 kg/m2；

t——时间。

1.3.2 多孔介质模型

满载时空气在物料层之间流动会受到粘性阻力以及惯性阻力的影响，因此本文将棉花层设置为六层多孔介质区域[18-19]。在Fluent中多孔介质区域需要确定孔隙率、粘性阻力系数以及惯性阻力系数。多孔介质的模拟即在标准流体流动方程中加入了动量源项[20]。源项由粘性损失项和惯性损失项两部分组成。

(6)

式中：Si——i方向上的(x，y，z)动量源项；

D、C——指定的系数矩阵；

|v|——速度大小。

对于简单均质多孔介质情况，可将公式简化为式(7)。

(7)

式中：α——渗透性系数；

C2——惯性阻力系数。

α与C2通过式(8)和式(9)求出。

(8)

(9)

Dp为多孔介质的当量直径，本文取为棉花的平均直径50 mm，棉花孔隙率φ通过孔隙率实验[21]测得棉花的自身密度ρ1以及堆积密度ρ2，然后根据式(10)计算，即可得到孔隙率约为70%。

(10)

1.4 边界条件

利用风速计采集入口9个点的风速及空气温度，采集数据如表2所示。

表2 入口速度温度采集数据Tab. 2 Inlet velocity temperature collection data

求得平均速度和平均温度分别约为10.1 m/s和42 ℃，作为进风口的边界条件；出风口设定为压力出口，表压设置为101 325 Pa；进出口的湍流强度以及水力直径通过式(11)和式(12)计算。

进出口的湍流强度

(11)

(12)

式中：Re——雷诺数；

d——圆管直径，在本模型中进风口为矩形，d可认为等于水力直径L。

L=4A/P

(13)

式中：A——进出风口的截面面积；

P——进出风口的截面周长。

具体边界条件设置参数如表3所示。

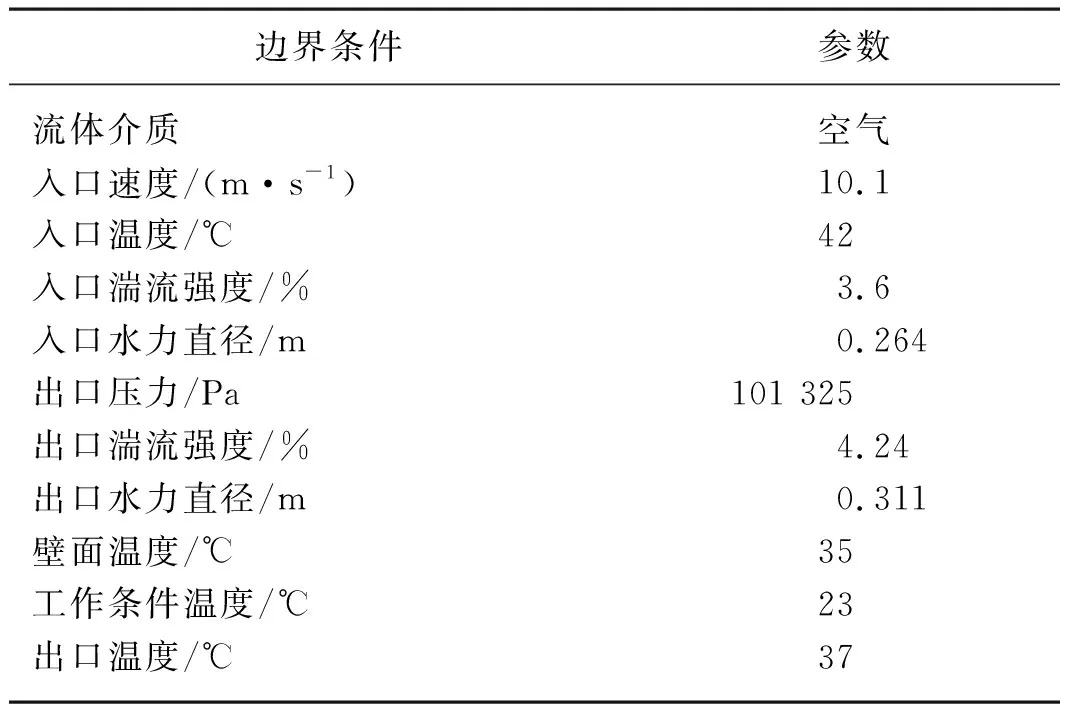
表3 边界条件参数Tab. 3 Boundary condition parameters

1.5 评价指标

1) 速度云图以及矢量图。在CFD仿真后处理中，通过速度云图[22-23]可以直观地反映流场均匀性以及分布特性，而风速过低时可引入速度矢量图来分析流场。

2) 相对标准偏差CV。为比较流场均匀性的改善程度，引入了相对标准偏差CV[24-25]。

(14)

式中：σv——平面内所有监测点风速的标准差；

vi——各监测点风速，i=1，2，3…；

n——平面内均匀分布的监测点数目。

相对标准偏差CV越大，表示烘房内部的流场越不均匀；CV越小，则表示流场越均匀。

3) 均匀性指数γv。均匀性指数[26]是基于统计偏差定义，可全面反映截面的流体速度分布特性。γv越大，表示流体流动均匀性越好。

(15)

1.6 Fluent仿真可靠性验证

为验证所建立CFD烘房模型以及仿真结果的正确性与可靠性，在实际烘房中三个高度平面上按图2所示每个平面取35个风速监测点，共105个点，利用风速传感器测量各点风速，并记录相对应点的仿真值，将实际测量值与仿真值进行对比，得到图3。

图2 测量点位置

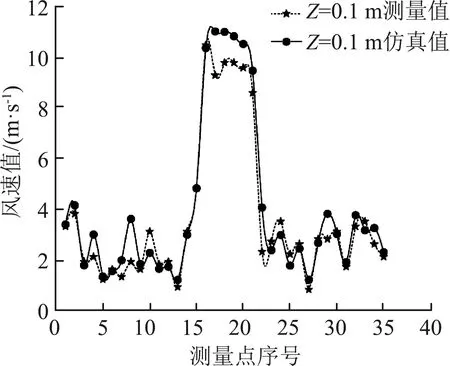
(a) Z=0.1 m处风速仿真值与测量值 (b) Z=0.8 m处风速仿真值与测量值 (c) Z=1.5 m处风速仿真值与测量值

由图3可知，三个平面上各35个监测点实测值与仿真值存在一定误差，但总体变化趋势基本一致，经计算得到实测值与仿真值的平均相对误差约为11.7%。在实际工程应用中，要求相对误差不应高于20%，因此本文的Fluent仿真中所建立CFD模型网格满足模拟要求，所选取求解器模型适用此烘房模拟，模拟结果符合实际情况，可知此CFD模型是具有可靠性的，可用于后续优化仿真方案的验证分析。

2 初始烘房模拟结果

2.1 初始空载烘房流场分析

对初始空载烘房仿真后，截取Z=0.1 m处平面的速度云图观察热空气进入烘房后在匀风区的分布情况，如图4(a)所示，烘房下部的匀风区热空气主要集中在中间部分，无法向两侧完全散开，呈现出匀风区两侧的风速明显低于中间风速，并在两侧形成对称的几处较大涡旋，初步分析是由于进风口宽度有限所致，这些涡旋会导致对应位置的烘干区部分区域空气流速很低，但本文中热泵的送风口宽度不可改变，所以需采取方案优化烘房进风口。

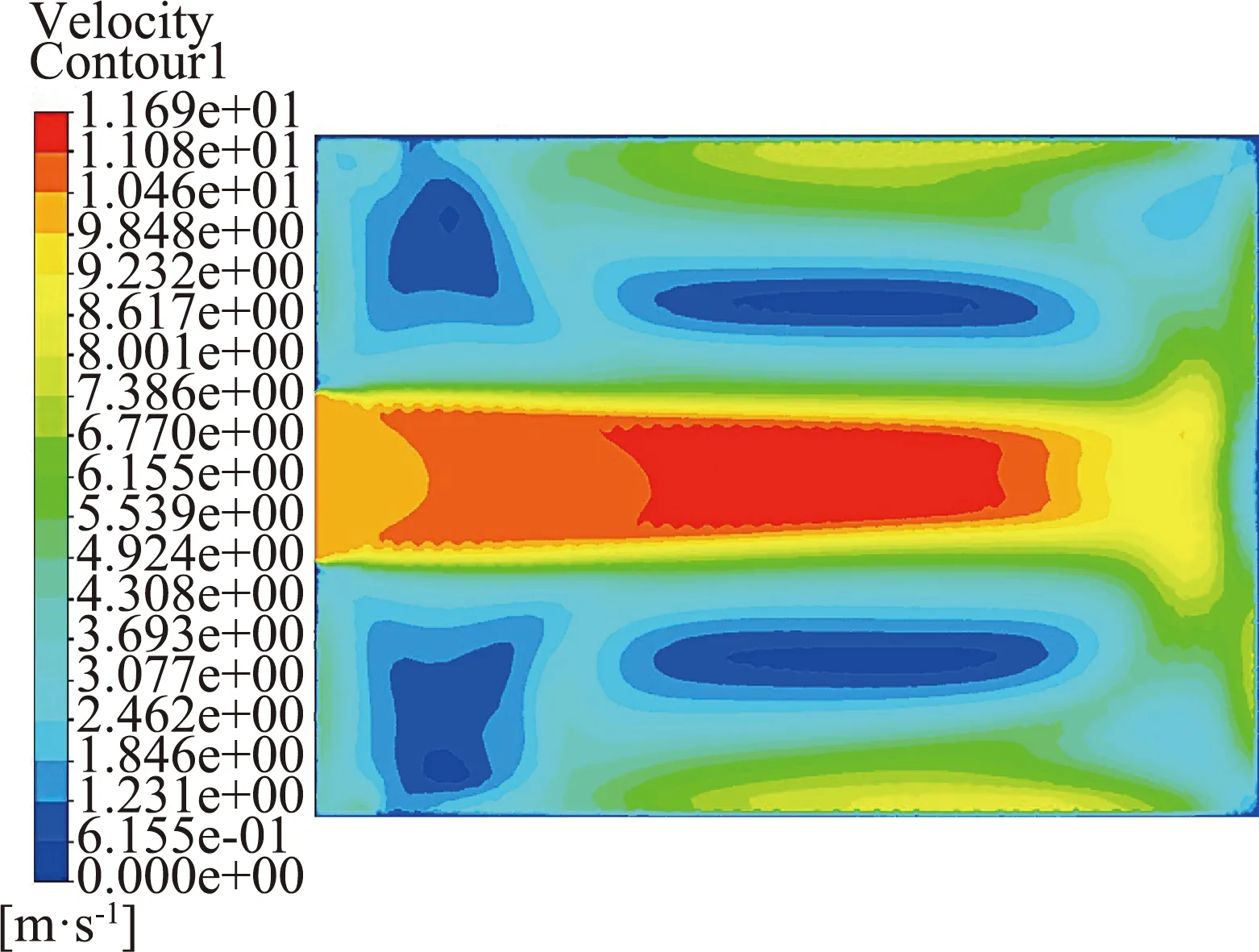
(a) Z=0.1 m处速度云图

由于内部空间较大，具有一定初始速度的热空气进入烘房后速度逐渐减弱并杂乱分散，受两侧涡旋影响，在中间位置有一小段热空气流速突然增大。为观察延X轴方向实际干燥区前后风场分布情况，截取了Y=0.6 m处速度云图，如图4(b)所示，具有一定压强的热空气进入烘房后直接冲击至烘房后壁面，导致很大一部分热空气从邻近后壁面的圆孔进入烘干区，在靠近进风口处，通过匀风板进入干燥区的热空气较少，后壁面附近风量明显多于进风口侧，并且由于进风口与出风口在同一水平面，导致不可避免地出现很大的涡旋。

另外，截取烘干区Z方向上的五个截面，并在各个截面选取20个风速监测点，处理得到初始结构下的烘干区五个截面的平均速度、相对标准偏差CV以及均匀性系数 的具体数值如表4所示，烘干区从下至上平均速度呈上升趋势，越靠近出风口风速越高，且各截面的相对标准偏差CV都比较高，均匀性系数均处于较低水平，流场整体均匀性较差。

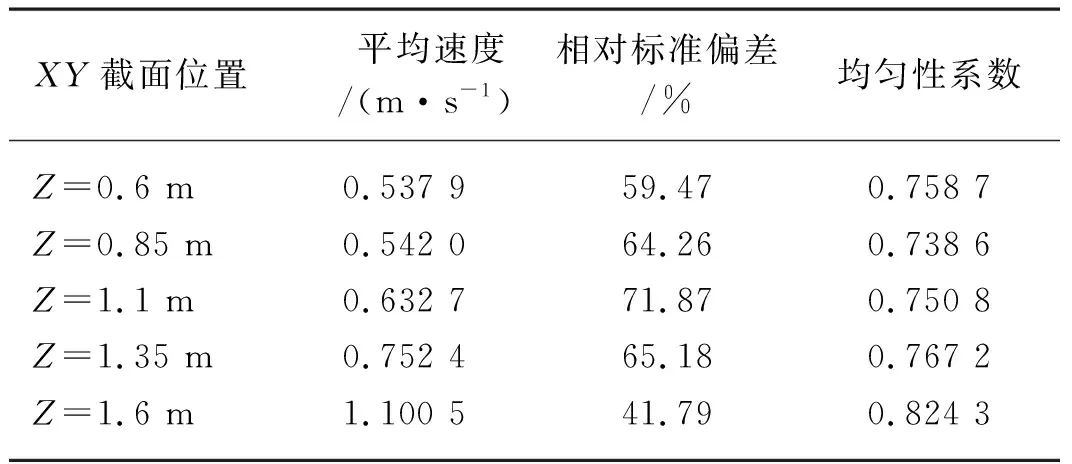
表4 初始结构烘干区XY面流场评价指标Tab. 4 Evaluation index of XY surface flow field in drying zone of initial structure

2.2 初始满载烘房流场分析

为观察满载时烘干区速度场情况，截取了XZ平面上Y=0.6 m处截面，得到图5所示速度云图。

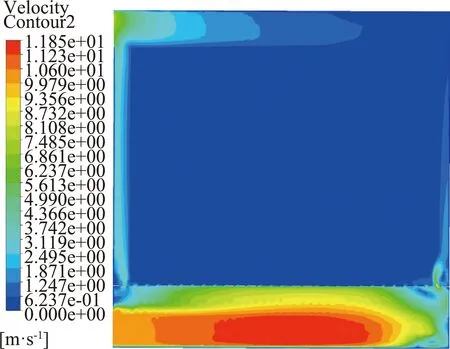
(a) 满载Y=0.6 m速度云图

由于多孔介质层之间的粘性阻力及惯性阻力的存在，导致风速过低，无法直观地观察到物料层之间的风场情况，因此引入速度矢量图来代替速度云图。从速度矢量图可以看出，具有一定初速度的热空气进入烘房后，从匀风板前后部进入烘干区热空气较多，由烘房中间部分进入物料层的热空气较少，这是由于物料层与烘房壁面间存在空隙，热空气沿空隙流向出风口。物料层由下至上，热空气始终受粘性阻力及惯性阻力影响，流动逐渐减少，有较多速度“缺口”，在物料层右上角出现风速“空白区”，是由于烘房内外压强差的存在导致附近热空气直接流向出风口。

3 烘房结构优化设计

为改善烘房由于进风口宽度有限导致的匀风区两侧风场不均的问题，在进风口处设置图6所示叶片用以导流，将进来的热空气充分扩散，减少匀风区涡旋情况。为使仿真快速有效地进行，在确定仿真方案之前，进行了叶片角度从15°～60°以15°为梯度差的预仿真，观察四种角度叶片对流场所造成的影响，结果显示：超过30°的叶片对热空气分散效果较差，因此最终选取了角度的三个梯度进行仿真分析，分别为10°、15°、20°。

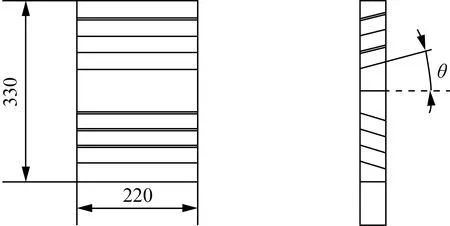
图6 进风口优化设计

针对初始烘房延X轴方向烘干区前后风场不均的问题，并为提高进入烘干区的热空气流速，将原有匀风板上的圆孔改为变径方孔，如图7所示。

(a) A类匀风板 (b) B类匀风板

由于变径方孔的存在，接近后壁面处匀风板上的方孔径较小，上升至烘干区的热空气随之变少，下方压强增大，促使热空气向匀风板中前部移动，使得匀风区的热空气在三个区域内能较均匀地上升至烘干区。从前到后，A类匀风板孔径为45 mm，35 mm，25 mm；B类匀风板孔径为40 mm，30 mm，20 mm；C类匀风板孔径为35 mm，25 mm，15 mm。

将上述的两种优化方法中进行组合，设计出9种方案，如表5所示。

表5 仿真方案Tab. 5 Simulation schemes

4 结构优化模拟结果

4.1 优化后空载烘房流场分析

为比较优化前后烘房内部横向风场变化，分别在原始结构以及9种优化方案得到的仿真结果中截取了XZ平面上Y=0.6 m处的速度云图，并在此截面烘干区范围内选取24个风速监测点，计算出各优化方案在此截面上的平均速度、相对标准偏差以及均匀性系数，如图8所示。

9种优化方案在XZ平面上较原始结构均大幅度提高了平均速度；除20°叶片下的3种优化方案外，另外6种方案也均大幅度降低了相对标准偏差并提高了均匀性系数。

为反映各方案烘干区不同高度平面的气流状态，截取了Z=0.6、0.85、1.1、1.35、1.6 m这5个平面的速度云图。在这5个平面上各选取了20个风速监测点，经处理后得到平均速度以及相对标准偏差的点线图如图9所示。

从图9中不同优化方案与原始状态下的截面平均速度和相对标准偏差对比可以看出，所有优化方案在XY平面上均不同程度提高了平均速度并降低了相对标准偏差。图9(a)中，在叶片10°的情况下，3类变孔径匀风板在提高整体平均速度方面差异不是很大，但图9(d)中B类匀风板的相对标准偏差整体处于下降趋势，且大幅度降低，而匀风板C与A的相对标准偏差在不同截面的波动较大，因此在10°叶片组中最优选为B匀风板。同理，在叶片15°以及20°的情况下，分别是匀风板B和匀风板C优化效果较同组其他方案效果更优。

(a) 9种方案Y=0.6 m处平均风速 (b) 9种方案Y=0.6 m处相对标准偏差 (c) 9种方案Y=0.6 m处均匀性系数

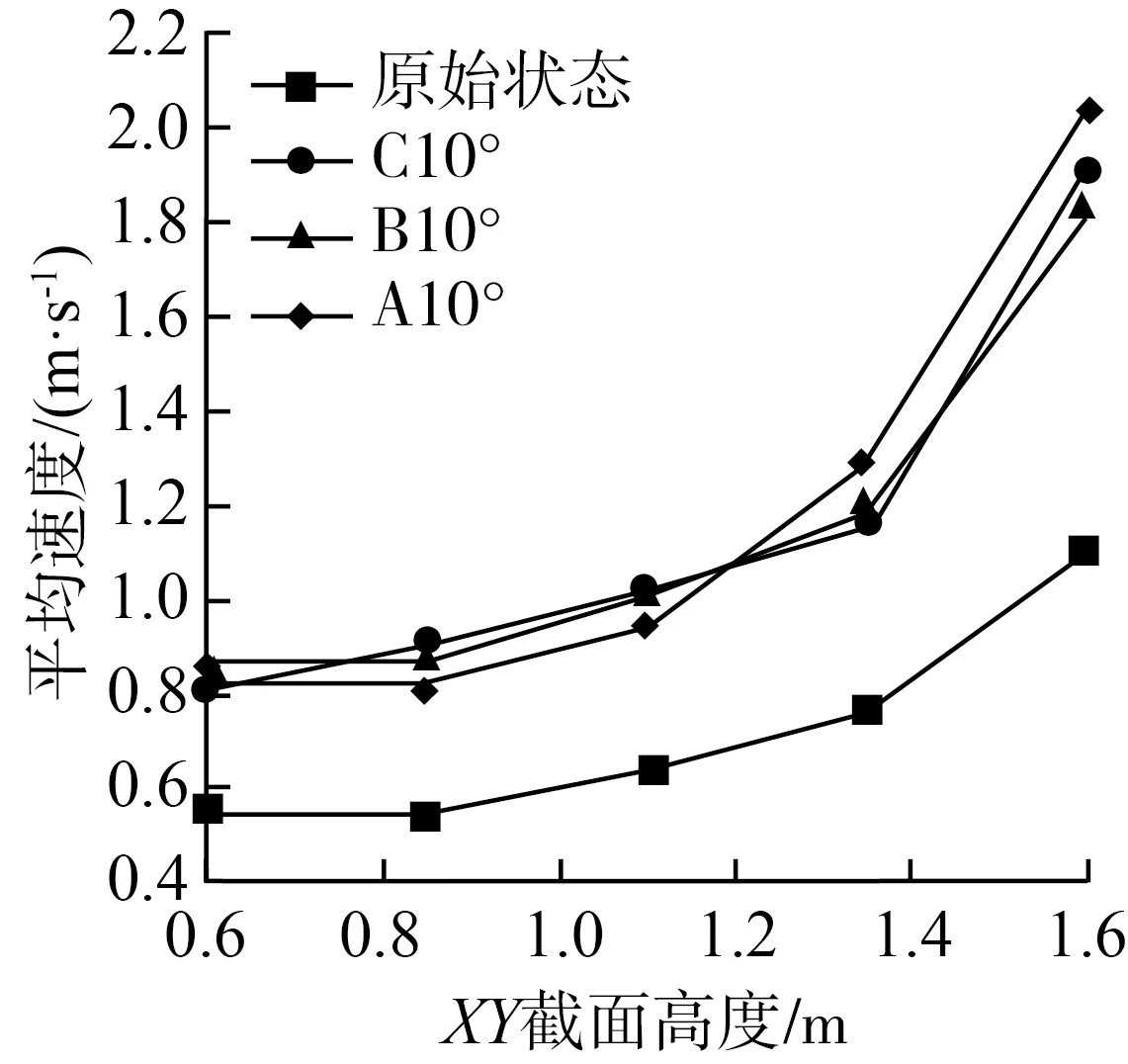
(a) 10°叶片下各方案平均速度 (b) 15°叶片下各方案平均速度 (c) 20°叶片下各方案平均速度

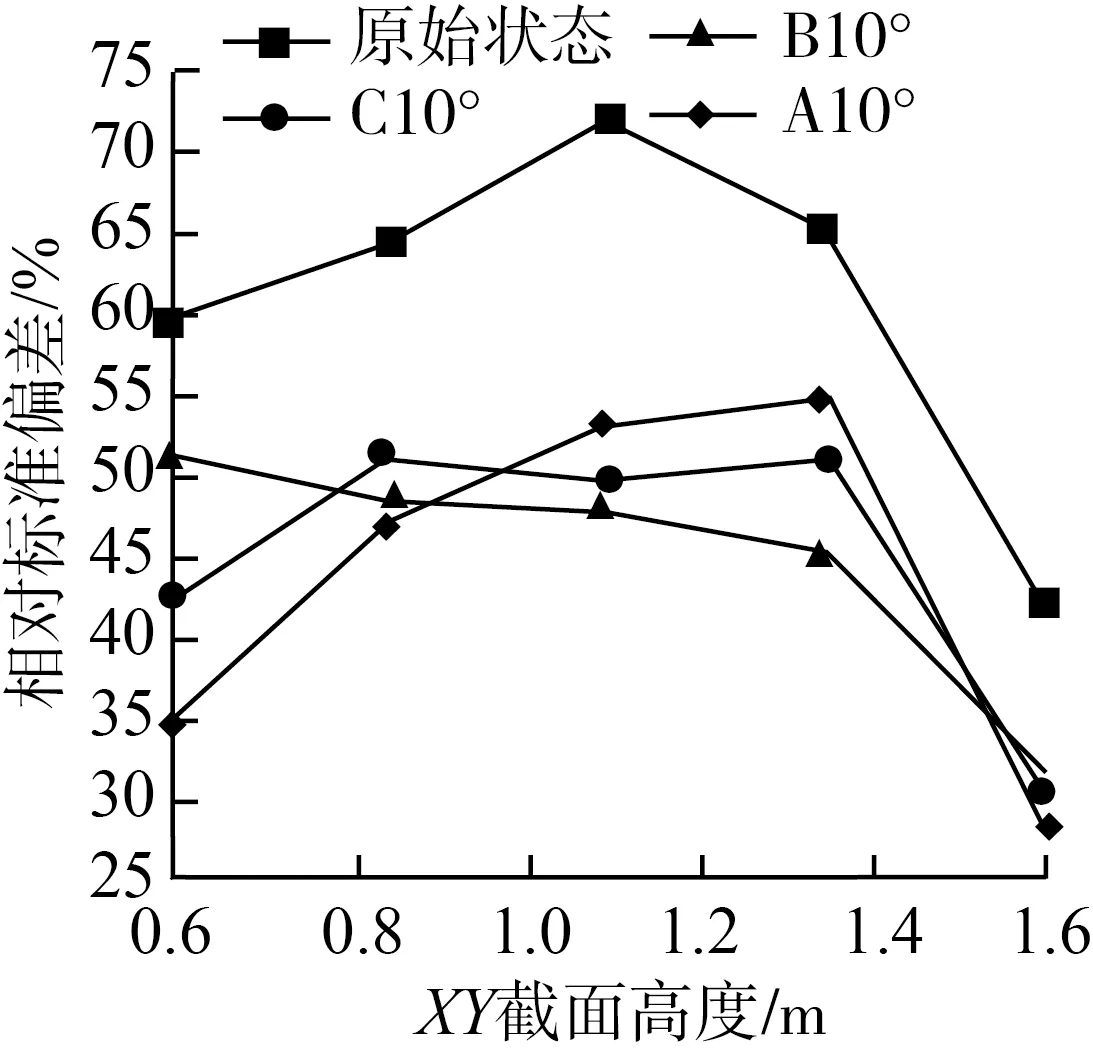
(d) 10°叶片下各方案相对标准偏差 (e) 15°叶片下各方案相对标准偏差 (f) 20°叶片下各方案相对标准偏差

4.2 确定最优方案

将上述各叶片下最优方案进一步对比，如图10所示。10°叶片与匀风板B在XY截面上的平均速度比另外两种组合较原始结构高出更多，但综合相对标准偏差，15°叶片和匀风板B一直处于下降趋势，比较稳定。

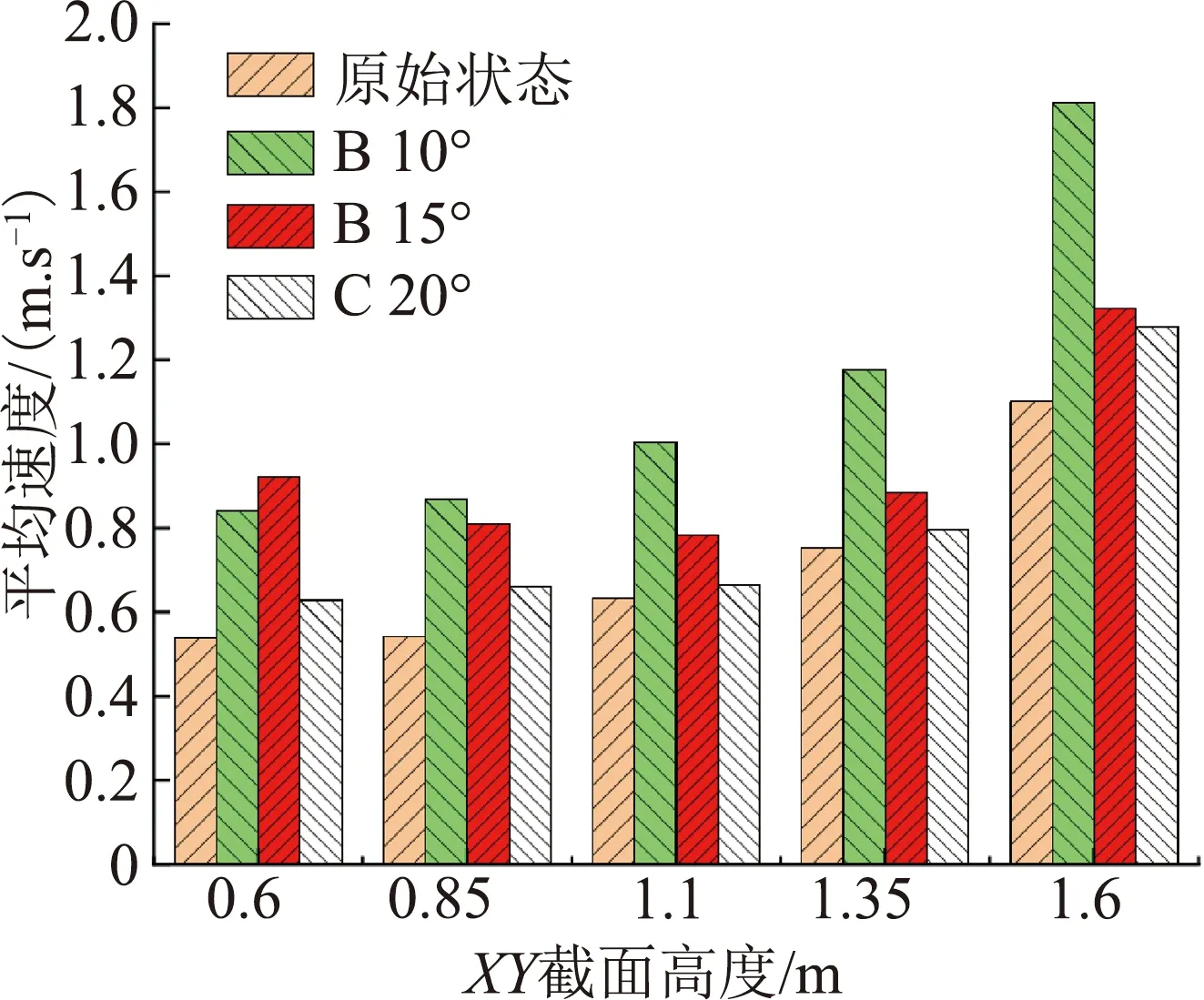
(a) 各组最优方案平均速度对比 (b) 各组最优方案相对标准偏差对比 (c) 各组最优方案均匀性系数对比

将所监测风速点进一步处理得到了各组最优方案的均匀性系数对比，可知15°叶片和匀风板B的组合下，各平面的均匀性系数均处于较好状态，且随着高度的上升均匀性逐渐增加。综合上述各评价指标，最终选定15°叶片和匀风板B为最优组合。

表6是优化后烘干区XY不同高度平面的平均速度、相对标准偏差CV以及均匀性系数的具体数据，与表4对比，各平面平均速度提高了0.231 m/s，平均相对标准偏差由60.51%降至38.87%，平均均匀性系数由0.76提升至0.85，烘干区由下至上，风速逐渐增大，风场愈发均匀。

表6 优化后烘干区XY平面流场评价指标Tab. 6 Evaluation index of XY plane flow field in drying zone after optimization

4.3 最优方案下满载烘房流场分析

优化前后对比如图11、图12所示。

(a) 优化前Y=0.35 m监测点风速 (b) 优化前Y=0.6 m监测点风速 (c) 优化前Y=0.85 m监测点风速

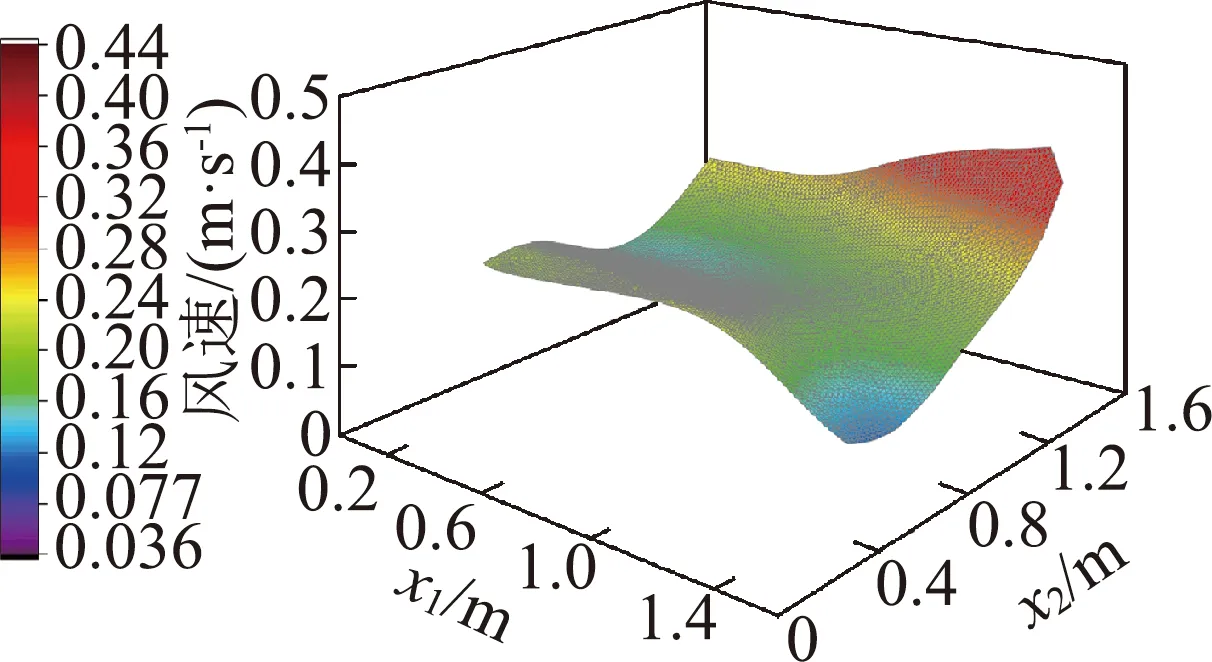
(d) 优化后Y=0.35 m监测点风速 (e) 优化后Y=0.6 m监测点风速 (f) 优化后Y=0.85 m监测点风速

(a) 优化前Z=0.5 m监测点风速 (b) 优化前Z=1.0 m监测点风速 (c) 优化前Z=1.5 m监测点风速

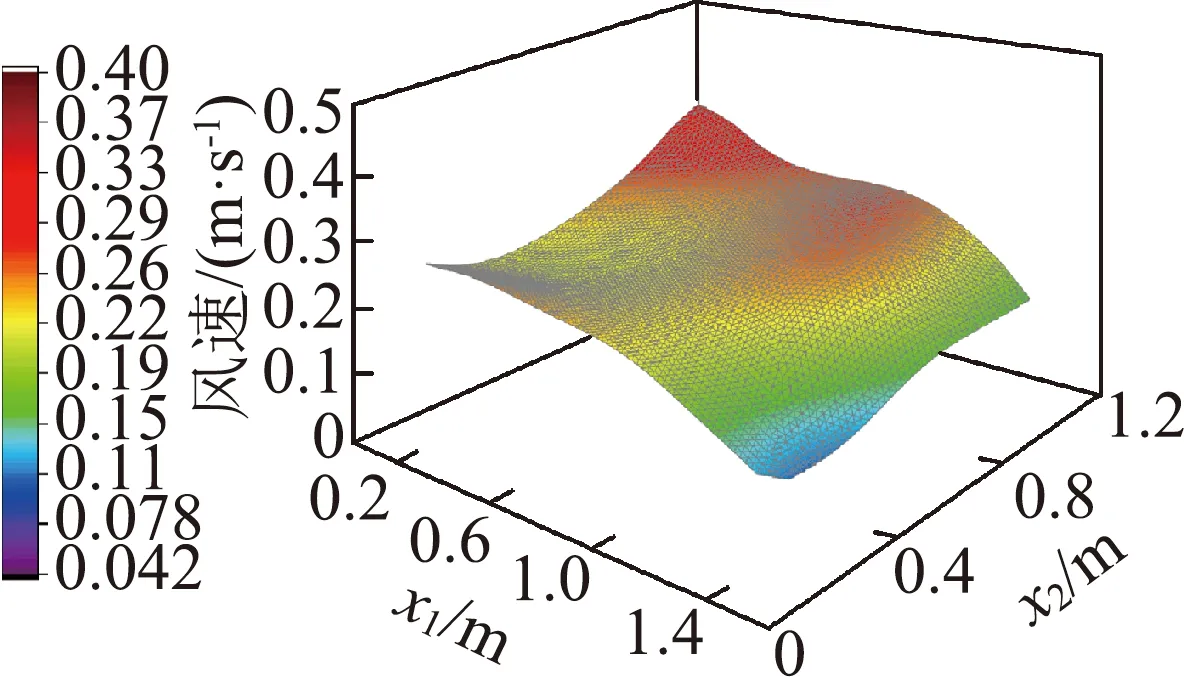
(d) 优化后Z=0.5 m监测点风速 (e) 优化后Z=1.0 m监测点风速 (f) 优化后Z=1.5 m监测点风速

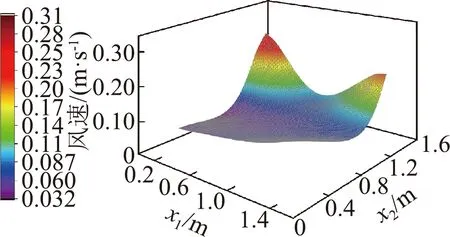
确定优化方案后，加入多孔介质并进行模拟仿真。为比较优化前后物料层内XZ不同位置平面的风场变化，使用ISO CLIP工具选定了Y=0.35、0.6、0.85 m三平面上处于物料层内部的部分截面，并各沿进风方向以及垂直进风方向选取了300个风速记录点，分别记为x1,x2。由图11可知，优化前后三个物料层内部截面的风场变化趋势相似；另外，原始烘房下在靠近进风口以及出风口侧风速过高，而其他位置的速度偏低，平均速度仅为0.087 m/s，优化后提升至0.2 m/s；原始烘房下的三维曲面图波动较大，三截面的平均风速相对标准偏差为44.8%，优化后降至25.1%，平均均匀性系数由0.84提升至0.91。

为了从烘干区XY不同高度平面上分析优化前后流场变化，同样使用ISO CLIP工具选定了Z=0.5、1.0、1.5 m三平面上处于物料层内部的部分截面，各取了300个风速记录点后绘制三维曲面图如图12所示。原始烘房下内部中间位置热空气流速很低，平均速度仅0.096 m/s，优化后被提高至0.23 m/s；另外，原始烘房在Z=0.5 m和1.5 m处速度波动很大，是因为这两处平面靠近进出风口侧，而Z=1.0 m由于处于物料层中部，其上各点风速极低，变化范围小，而优化后的烘房风场变化显然更加平稳，经结构优化后平均相对标准偏差由30.1%降至24.32%，且优化后三平面的速度均匀性系数均在0.9以上，平均均匀性系数由0.88提升至0.94。

5 结论

本文基于Fluent软件对气流上升式热泵烘房流场进行了模拟仿真，在验证了仿真模型的可靠性与正确性的基础下完成了结构优化。

1) 通过在进风口设置不同角度导流叶片，并且将匀风板上原有的统一直径圆孔改为变径方孔，共设计了9种优化方案组合。通过比较速度云图、速度矢量图、平均速度、相对标准偏差以及均匀性系数，最终确定15°导流叶片与B类匀风板的组合为最优组合。

2) 优化后的烘房相较于初始烘房，烘干区平均速度提高了0.231 m/s，烘干区XY不同高度平面的平均相对标准偏差CV由60.51%降至38.87%，平均均匀性系数由0.76提升至0.85；满载时烘干区物料层范围内XZ不同位置平面的平均速度0.087 m/s增强至0.2 m/s，平均相对标准偏差CV由44.8%降至25.1%，平均均匀性系数由0.84提升至0.91；烘干区物料层范围内XY不同高度平面的平均速度由0.096 m/s增强至0.23 m/s，平均相对标准偏差CV由30.1%降至24.32%，平均均匀性系数由0.88提升至0.94，即优化后的烘房流场整体低速区域大大减少，流场均匀性有效得到改善，将更有利于实际烘干，从而提高产品的最终干燥效果。本研究可为气流上升式热泵烘房的优化设计提供理论方法及技术方案。