基于热仿真的模块散热结构设计及优化

谢 攀， 何 翔， 李文杰， 王 轩， 王一丁

(成都四威功率电子科技有限公司， 成都 610097)

随着中国经济的高速发展，城市土地资源日趋紧张，供电需求日益旺盛，变电站的小型化和紧凑性设计已然成为主流趋势，其中使用的电子设备的器件集成度和功率密度越来越高[1]，设备内部的热量和热流密度急剧上升，常规的结构设计无法满足产品的散热需求。为了解决大功率-高功率密度产品的散热问题，国内外很多研究者长期以来针对电子产品的散热优化进行了大量研究[2-5]，将新产品[6-7]和新工艺[8]应用到产品结构设计过程中，保证了产品散热的有效性和工作的可靠性。

为提升大功率模块在强迫风冷设备中的散热效果，满足户内电站小型化和紧凑性设计的需求，笔者以一种大功率-高功率密度功率放大模块为研究对象，结合其工程应用，对比分析常规散热结构和优化散热结构的散热性能，给出了产品的优化设计思路，可为同类产品的工程应用提供参考。

1 物理模型

功率放大模块结构见图1，模块外形尺寸为200 mm×120 mm×32.5 mm，将热源简化为1个86 mm×27.5 mm的面热源。热源焊接在功率放大模块内腔底部，仿真计算时可忽略热源和模块之间的接触热阻。热源功率为450 W，设计要求其在稳态工作时的表面温度不超过105 ℃。

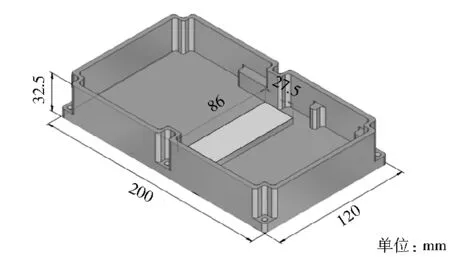
图1 功率放大模块示意图

1.1 常规散热模型1

常规散热模型1通常是在模块底面(散热面)贴合散热器，通过散热翅片与冷风的强迫对流散热。采用强迫风冷结构设计时，需要形成良好的风道。为了充分利用分机的安装空间和风机选型，针对模型1设计的散热结构见图2。该模块采用中间是风道、两边是模块的对称结构，2个散热器的总高度和模块宽度相近，可安装最大占地尺寸是120 mm×120 mm的风机，散热器为一种工业常用的焊接鳍片散热器，具体参数见表1。风机安装罩主要用于仿真阶段形成密闭风道和风机模型设置。

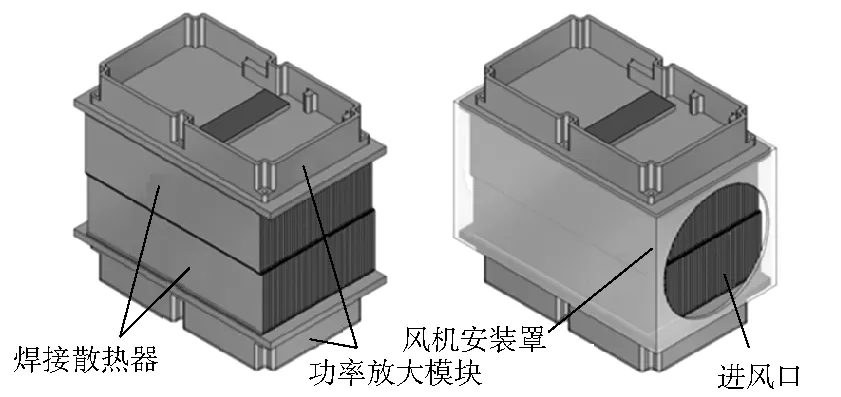
图2 模块散热结构示意图

表1 焊接散热器参数

1.2 优化散热模型2

模型2是在模型1的基础上，优化了功率放大模块腔体结构，散热器保持不变，其模块结构见图3。具体措施是在模块腔体底部嵌入热管，热管通过高温焊料与模块腔体焊接成整体。对于热管底部与盒体底面所组成的平面，其整体平面度不高于0.1。图3中的热管直径、数量和排列形式是当前算例的其中一种方式，在类似产品设计时，可进一步优化，总体原则是将热管的两端分别放置于高热量区域和低热量区域。模型2整体效果见图4。

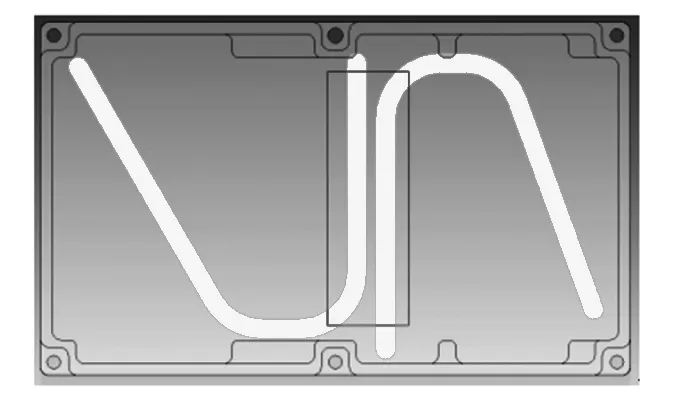
图3 模型2模块腔体示意图

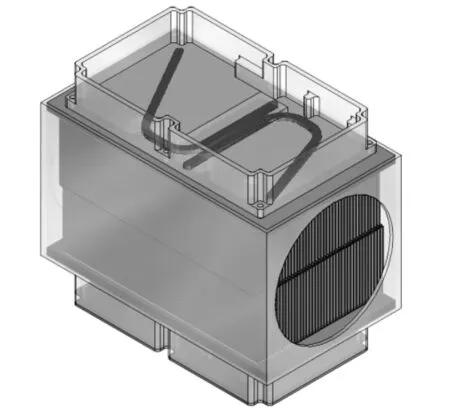
图4 模型2整体效果图

1.3 优化散热模型3

模型3是在模型1的基础上，优化了散热器结构，功率放大模块腔体保持不变，具体见图5。具体措施是在散热器基板和鳍片之间嵌入热管，热管通过焊料与基板和鳍片焊接成整体。图5中的热管形状、直径、数量和排列形式是当前算例的其中一种方式，在类似产品设计时，可进行优化，总体原则是将热管的两端分别放置于基板高热量区域和鳍片远离基板一侧，嵌入鳍片的热管应均匀分布。模型3的整体效果见图6。

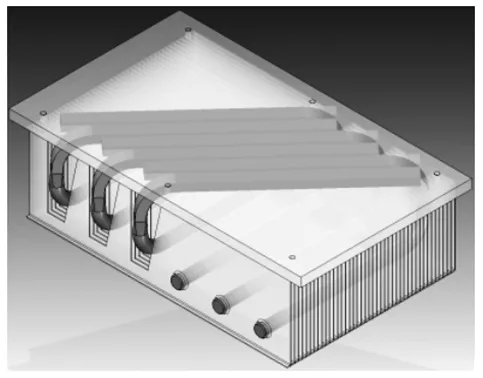
图5 模型3散热器示意图

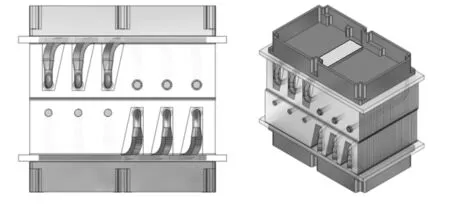
图6 模型3整体效果图

1.4 优化散热模型4

模型4是模型2和模型3的组合，针对模块腔体和散热器均进行了优化，功率放大模块的改进方式和模型2相同，散热器的改进方式和模型3相同，其整体效果见图7。

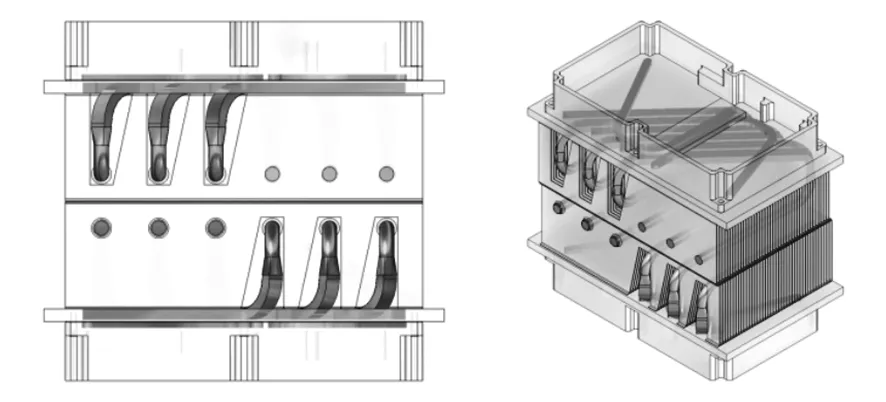
图7 模型4整体效果图

2 理论计算

2.1 风量计算

对强迫风冷产品进行热设计时，首先要根据设备内部的总热耗计算冷风需求量。功率放大散热组件由2个功率放大模块和2个散热器组成，组件的总热耗为900 W。在强迫风冷散热模型中，自然对流和辐射传热所散去的热量比例很小，一般认为所有热量通过强迫对流的冷风带出设备，具体计算公式[9]为：

Qf=Q总

(1)

式中：Qf为冷风流经设备的吸热量，W；Q总为设备总热耗，W。

热量计算公式[10]为：

Qf=cp·qV·ρ·ΔT

(2)

式中：cp为空气的比定压热容，取1 005 J/(kg·K)；qV为冷风的体积流量，m3/s；ρ为空气密度，取1.093 kg/m3(50 ℃的干空气物性参数)；ΔT为出口热空气平均温度和进口冷空气平均温度的差，理论计算时可取10～20 K。ΔT越小，计算得出的风量越大，散热效果更好；ΔT越大，计算得出的风量越小，散热效果相对较差。在本文中的ΔT取10 K。

由式(1)和式(2)可得：

qV=Q总/(cp·ρ·ΔT)

(3)

通过计算可得到冷风体积流量为0.082 m3/s(4.92 m3/min)。

2.2 风机选型

通过2.1节风量计算得到的冷风流量为设备实际所需的风量，在风机选型时，风机手册中通常提供的是最大流量(压力为0 Pa时)，此时可结合工程实际，假设风机工作点的风量为最大风量的50%，则可按照2倍计算得到的冷风流量，对照风机手册进行选型。确定风机型号时，还应结合结构布局，在对应的可安装的风机外形尺寸范围内，综合考虑风压、风机数量、功耗、噪声和启动电流等因素，选出风量满足要求的风机。

功率放大散热组件的风机占地尺寸如果超过120 mm×120 mm，会影响分机结构布局的紧凑性，因此将风机占地尺寸限制在120 mm×120 mm以内进行选型。查阅风机手册后，最终选择型号为M12038VD2的风机进行数值计算，风机的参数见表2，风机的流量和压力曲线见图8(“V”、“H”、“M”、“L”表示不同转速下的流量和压力曲线)中的“V”所示。

表2 M12038VD2型风机工作参数

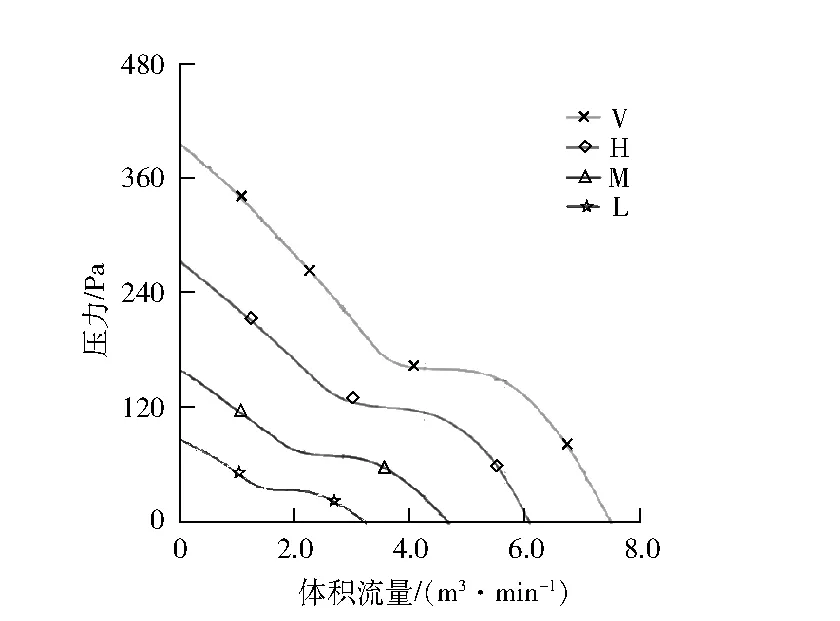
图8 M12038VD2型风机流量和压力曲线图

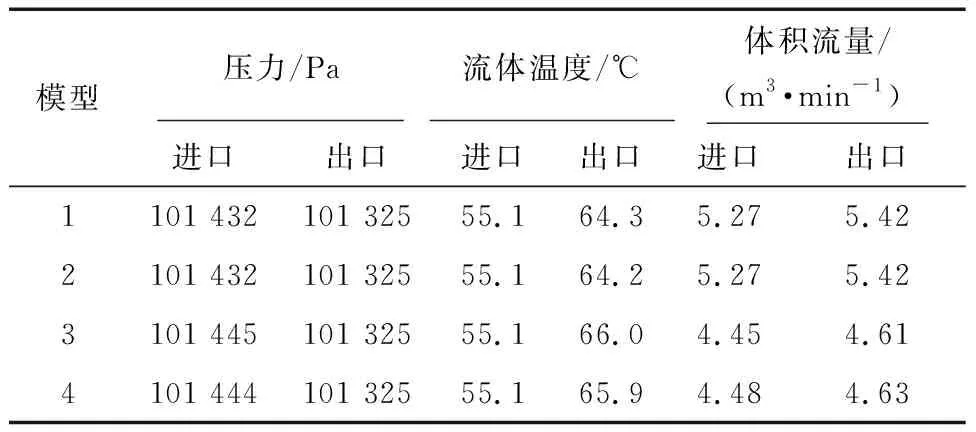
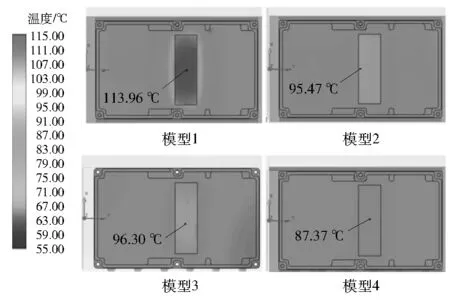
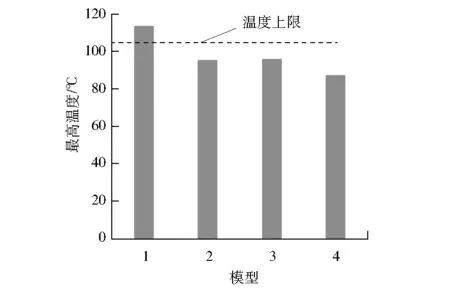
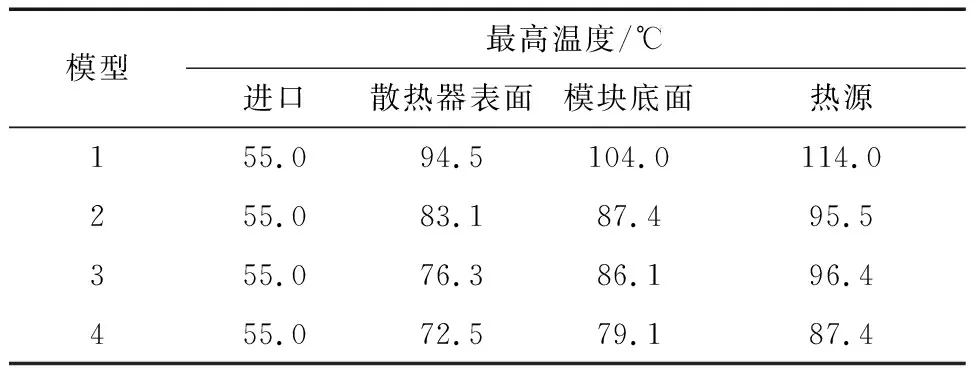
结合表2和图8可得：该风机的最大体积流量qV,max为7.55 m3/min，即qV

3 数值仿真

3.1 模型简化

数值仿真基于FloEFD软件完成，为节省计算资源，选择内部流动模型，此模型要求必须形成密闭风道，因此将4种散热结构进风口和出风口通过“创建封盖”功能创建实体堵住，后续再通过设置风机和边界条件形成流动的腔体。

3.2 仿真设置

4种模型的仿真设置除热管模型不一样，其余冷却条件均一致，具体情况如下。

(1) 模型1：内部流动模型；默认流体为空气；固体材料为AL6061；外壁面为绝热壁面；环境温度为55 ℃；风机为外部进口风扇，导入图8中的“V”曲线；边界条件为环境压力开口；热源为2个450 W的面热源；功率放大模块和散热器基板贴合面设置一层厚度为0.1 mm、导热系数为1 W/(m·K)的接触热阻；初始网格级别为4级，最小间隙尺寸为2 mm。

(2) 模型2：在模型1的设置基础上，增加位于模块腔体的4个热管模型。

(3) 模型3：在模型1的设置基础上，增加位于散热器的12个热管模型。

(4) 模型4：在模型1的设置基础上，增加16个热管模型。

4 结果分析

4.1 风量校核

从数值计算结果中的“表面参数”获取的4种模型风道进口和出口的温度、压力和流量见表3，其中：进口压力是风机安装面的平均压力，计算时设置的是吹风模型，进口的压力最高；出口压力均设置为环境压力；进口温度为风机从环境中吸入冷风的温度，均为55 ℃(室外环境工作温度上限)左右；出口温度为冷风流经风道吸热后的实际平均温度，与流量相关。

表3 风道进口和出口截面参数

4种模型除散热器存在差异，其余冷却条件一致。模型1和模型2的散热条件和散热器相同，流动阻力均为106.8 Pa，温升分别为9.23 K和9.13 K；风机进口体积流量为5.27 m3/min。将ΔT分别调整为9.23 K和9.13 K，并代入风量计算公式，计算得出风机进口体积流量分别为5.32 m3/min和5.38 m3/min，此时数值计算结果和理论计算结果的相对误差在2.1%以内，说明数值计算结果准确。模型3和模型4的散热器在模型1的基础上嵌入了热管，流动阻力分别为120.7 Pa和119.2 Pa，说明增加热管后风道内部的流动阻力变大了；与此同时，风机进口体积流量分别降低为4.45 m3/min和4.48 m3/min，符合“风机曲线相同时，流动阻力越大，风量越小”的理论预计；此外，温升分别为10.94 K和10.84 K时，将其代入风量计算公式中的ΔT后计算得出风机的体积流量分别为4.49 m3/min和4.53 m3/min，数值计算结果和理论计算结果的相对误差也在1.5%以内，说明数值计算结果准确。

模型1和模型2的风量大于qV，说明这2种模型的流动阻力较小，风机工作点位于曲线右侧，实际风量满足选型计算的要求；模型3和模型4优化了散热器，增加了风道内部的流动阻力，导致风机工作点左移，实际风量小于qV，流体温升比模型1和模型2增加了约1.7 K，需要结合热源温度，才能判断散热器改进后是否优化了散热性能。

4.2 流场分析

4种模型的流场压力见图9。由图9可得：模型3和模型4的风机进口压力高于模型1和模型2，这是因为增加热管以后，相当于在风道内部增加了阻挡区域，导致流动阻力增加，风的扰动增强。

图9 4种模型的流场压力

4种模型的流场温度见图10。由图10可得：无论是对模块腔体还是对散热器进行优化，都会对流场的温度产生影响。模型1是常规结构，热量相对集中，流场高温区域较为明显；模型2优化了模块腔体，降低了模块底面的热流密度，流场温度也更均匀；模型3优化了散热器，将一部分热量从散热器基板直接快速传导至鳍片中间，使远离基板一侧的鳍片间的冷风也能有效参与换热；模型4是模型2和模型3的组合体。

图10 4种模型的流场温度

4.3 温度分析

由于4种模型均为对称结构，并且计算时不考虑重力的影响，上、下两组模块和散热器的温度云图相同，仅针对每种模型的一组模块和散热器分析其温度。图11为功率放大模块腔体内表面的温度云图，4种模型的最高温度点均位于简化面热源处。模型1、模型2、模型3、模型4的最高温度分别为113.96 ℃、95.47 ℃、96.30 ℃、87.37 ℃。

图11 模块腔体(含热源)表面温度云图

图12为散热器基板上表面的温度云图。由图12可得：模型1和模型2未优化散热器，基板的温度分布趋势和模块腔体的温度分布趋势一致；模型3和模型4优化了散热器，基板的温度分布比模块腔体的温度分布更加均匀。

图12 散热器基板上表面温度云图

4种模型的热源表面的最高温度和热源表面温度上限的对比情况见图13。由图13可得：模型1的最高温度超过了温度上限9.0 K，不满足使用要求；模型2、模型3和模型4的最高温度比温度上限分别低了9.5 K、8.7 K和17.6 K，均满足热源使用要求，模型4的散热效果最优。同时，结合4.1节风量校核中的所述内容，虽然优化散热器后增加了流动阻力并导致风机工作点风量低于理论计算值，但是模型3和模型4的散热效果却明显提升，说明优化思路是正确的。

图13 模型最高温度对比

热源中心截面各点的最高温度见表4，其中：散热器表面温度和进口风温度的差可表征散热器和冷风之间的换热能力，温差越大，散热效果越差；模块底面温度和散热器表面温度的差可表征热源下方接触热阻层的热阻，温差越大，热阻越大；热源温度和模块底面温度的差可表征模块内部热阻，温差越大，热阻越大；热源温度和散热器表面温度的差可表征模块到散热器之间的综合热阻，温差越大，综合热阻越大。

表4 热源中心截面温度参数

对比分析模型2和模型1的物理模型和仿真结果可得：模型2的腔体中嵌入热管以后，热源处的部分热量可沿着热管排列路径快速传递至腔体其他区域。该措施降低了热量在模块内部传递的热阻，直接体现为模块腔体的温度更加均匀，热源温度和模块底面温度的差由10 K降低为8 K；另一方面，接触热阻层的热量输入端(模块底面)热量分布更加均匀以后，接触热阻层的温升也由9.5 K降低至4.3 K；与此同时，散热器基板的热量输入也变得更均匀，虽然散热器未进行任何改动，散热器的综合换热效果仍变得更好，散热器表面和进口风温度的差由39.1 K降低为28.1 K。综合以上分析，在模块层面进行优化，有利于强迫对流模型全散热过程冷却效果的提升。

对比分析模型3和模型1的物理模型和仿真结果可得：将模型3的散热器中嵌入热管以后，基板高热量区域的部分热量可沿着热管排列路径快速传递至远端鳍片中间。该措施降低了热量从基板传递至远端鳍片的热阻，直接体现为散热鳍片之间的流场更加均匀(见图14)，散热器表面温度和进口风温度的差由39.1 K降低为21.3 K，极大地提高了散热器的综合换热效果。由于模型3未优化模块腔体结构，热源温度和散热器表面温度的差为20.1 K，和模型1的19.5 K大致相等，说明优化散热器并未对模块内部产生明显影响。

图14 模型1和模型3风道流场

模型4的优化机理与模型2和模型3相同，是散热器层面和模块层面的组合形态，可用于极端工况产品的优化设计。

5 结语

强迫风冷散热结构是大功率-高功率密度模块比较常用的冷却方式，以一种功率放大模块为例，设计了1种常规风冷结构和3种优化结构，基于理论计算和数值仿真验证了优化设计思路的可行性和有效性，得到以下结论：

(1) 通过优化模块结构，例如在模块底部嵌入热管，可降低模块内部的热阻和模块底面的热流密度，同时还能加强散热器的换热效果，降低热源温度。

(2) 通过优化散热器结构，例如在基板和鳍片间嵌入热管，可提高散热器的对流传热能力，虽然无法降低模块内部的温度梯度，但仍能降低热源温度。

(3) 同时对模块和散热器结构进行优化，可在最大程度上优化组件的散热效果。

3种优化结构均可降低热源的最高温度，模型2和模型3的优化效果相当，模型4的优化效果最好。在进行产品结构设计时，还应当综合考虑器件参数、加工工艺和成本等因素。内部器件的热流密度相对较高时，可通过模型2进行优化；模块总热量较大，但是内部器件的热流密度相对较低时，可通过模型3进行优化；模块的总热量和内部器件的热流密度均较大时，可通过模型4进行优化。