基于新能源汽车事故特征的驾驶人伤害风险预测模型研究

文图｜黄钢 姜良维 苏婉

近年来，我国新注册的新能源汽车总量呈持续快速增长趋势，由此带来的安全问题也日益严峻，新能源汽车肇事致人伤亡的交通事故致死率远高于传统燃油汽车，加强道路交通事故特征深度分析尤为必要。目前，我国的道路交通事故分析侧重于传统燃油汽车，而新能源汽车的“三电”系统构造与传统燃油汽车存在较大的差异，特别是在汽车控制、制动、动力等多个维度上。鉴于新能源汽车事故特征研究起步晚、深入程度低，故本文从新能源汽车事故的肇事驾驶人入手，通过人、车、路、环境等多个维度的事故数据深度分析，对筛选出与肇事驾驶人伤害风险较为相关因素进行不同维度的统计分析，并通过逻辑回归算法，研究建立新能源汽车事故驾驶人伤害风险的预测模型，进一步探讨模型优化方法，通过模型融合提升算法精度，期望为挖掘新能源汽车事故特征提供依据、为新能源汽车安全风险管控提供参考。

一、特征统计分析

（一）事故数据

本文使用的新能源汽车事故数据来源于公安交通管理综合应用平台，为2019-2021 年三年的新能源汽车肇事造成人员伤亡的事故数据21676 条。一是与交通事故基本信息相关的数据，如事故发生时间、天气、地点等；二是和交通事故人员相关的数据，包括车辆信息和人员信息，如车辆信息中的车辆类型、车辆品牌、车辆号牌等，人员信息中的年龄、性别、文化程度等。按照《道路交通事故信息调查》（GA/T 1082）公安行业标准要求，采集的事故相关数据多达数百种，如果全部纳入本文分析的话，将会极大地增加数据处理的复杂度，也不利于事故特征挖掘。为此，本文未考虑与新能源汽车事故本身无关或弱相关的参数，避免这些数据的存在造成模型求解带来大量的负荷及影响模型求解的精度。

首先，挑选出与新能源汽车驾驶人伤害风险（即是否死亡）高度相关的数据特征。因部分特征数据中存在空值，对于空值占比少于5%的特征值，本文采用拉格朗日方法进行填充。对于空值占比较大的“文化程度”这一特征，本文对数据进行了均值填充。

随后，选择统计学中的常用Pearson 相关系数，计算全部数据与新能源汽车事故中人员伤害风险的相关系数，如表1 所示。随后，挑选出事故原因、事故形态、车辆品牌等12 种相关系数排名最靠前的事故参数，选择依据为相关系数大于0.3 的特征。Pearson 相关系数计算方法见式（1）。

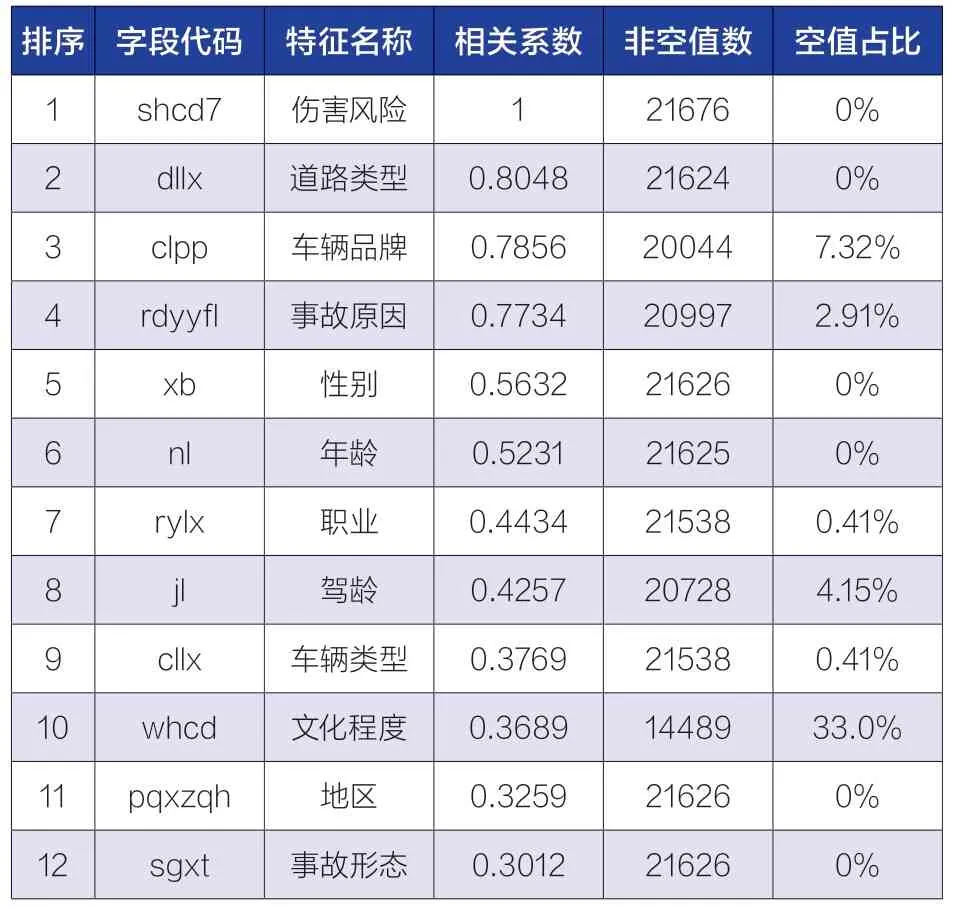
表1 与当事人伤害风险相关性最强的特征值

式中：X、Y为待求解相关系数的两个样本特征；E为期望值。

通过相关系数的计算，本文选择以上数据作为研究驾驶人伤害风险预测研究的数据特征进行模型构建。

（二）数据处理

为降低计算复杂度及减少数据项中冗余与数据维度，本文对表1 中的部分字段数据进行合并，即伤害风险变为二分类变量，即死亡和非死亡；事故原因仅保留主要项；车辆品牌保留事故量最多的十种车；职业、车辆类型、文化程度的数据项进行了数据值的整合处理（如车辆类型中的小型客车细分项包括小型轿车、小型面包车、小型越野客车等十余项，为方便数据处理，统一整合为小型客车）。此外，驾驶人的年龄和驾龄是两个连续变量，变化幅度较大，在进行回归分析时，会极大地影响收敛速度，对这两个变量进行了归一化处理。图1 为本文对原始数据处理后的主要特征分布。其中，新能源汽车事故中死亡的肇事人非常少，占比不到1%；城市道路新能源汽车事故最多，占比超过3/4，其次是农村道路，占14%，国省道占10%，这与新能源汽车使用场景一致；新能源汽车肇事人死亡事故中，肇事人年龄主要分布在20 至60 岁之间，而非死亡的肇事人则10 岁以上都有分布；各文化程度的肇事人密度分布规律基本一致；中南、华东片区新能源汽车事故明显多于其他四个片区，这与新能源汽车拥有量分布一致。

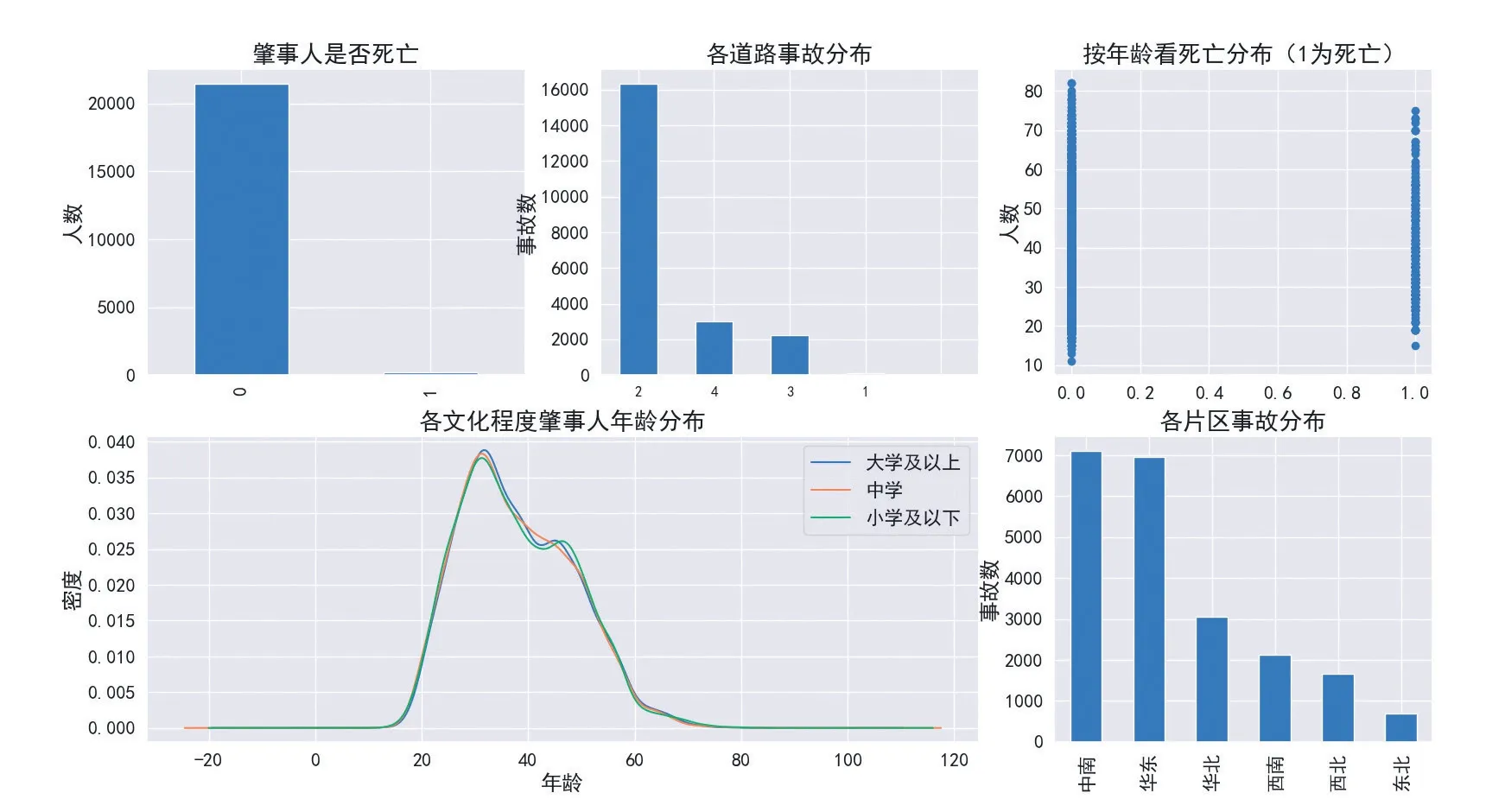
图1 新能源汽车事故特征

二、预测模型及优化

（一）模型构建

基于上述新能源汽车事故特征统计分析，本文构建的逻辑回归模型如式（2）所示。

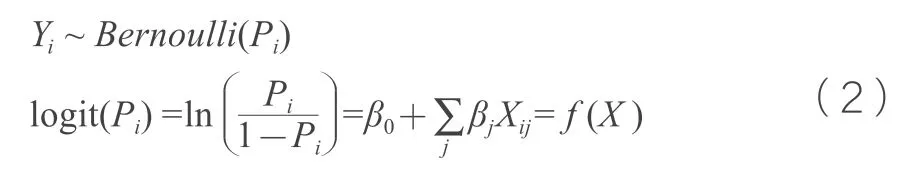
式（2）中的Yi为第i 起事故中肇事人的伤害风险，Pi为第i起事故肇事人死亡的概率，β0为模型截距，βj为第个j特征的参数，Xij为第i起事故肇事驾驶人的第j个特征因素的值。Xij可以是非车辆因素的一阶效应或多阶交互效应，例如事故形态—道路类型二阶交互效应。

本文重点研究新能源汽车事故中驾驶人在事故中所受伤害是否为死亡，是一个典型的二分类问题，而逻辑回顾算法在二分类问题中的先进性已得到广泛的验证和认可，因此，本文将使用逻辑回归算法来构建新能源汽车事故中驾驶人是否死亡的预测模型，并对原始算法进行不断优化，提升模型预测的准确性。

针对本文使用的数据，将原始数据集的80%作为测试集、20%为验证集，即可将数据代入上述模型进行训练，得到完整的逻辑回归模型，并利用验证集核对模型的精度。如表2 为处理结果。

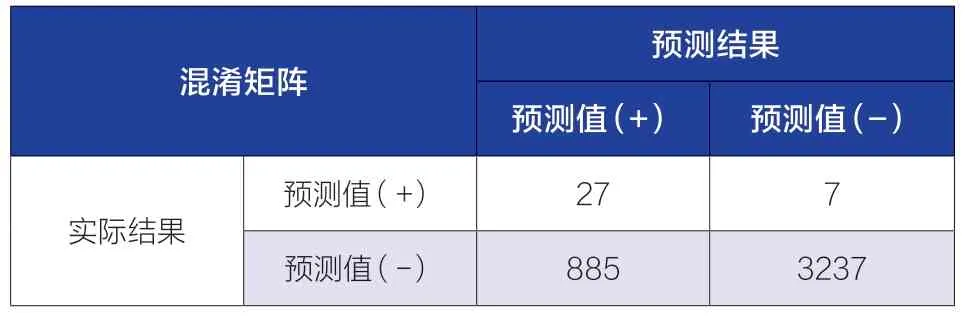
表2 逻辑回归模型在验证集上的混淆矩阵

通过表2 中的混淆矩阵，原始逻辑回归模型的算法精度（正确分类样本所占的比例）为0.785，精确率为0.794，召回率（正确预测为正类的占全部实际为正类的比例）为0.027。模型的准确率和精确率尚可，召回率偏小，具有较大的提升空间。

（二）交叉验证

交叉验证是一种防止因模型复杂而导致过拟合的科学数据处理方法，使用交叉验证可以提高机器学习模型的精度。其原理是对样本数据进行切割，将大样本量数据转化为较小子集。首先，在一个子集上进行训练得到初始模型，而其他子集则用来确认及验证此次分析的准确性。通过交叉验证，可以提高机器学习算法对非训练数据的数据集的泛化能力。本文采用十折交叉验证方法，将数据集分成10 份，并依次将其中的9 份数据作为训练数据，剩下1 份作为测试数据依次进行模型训练。每次训练都会得出所建立模型相应的准确率。最后，将10 次训练结果的准确率的平均值作为对算法精度的综合估计，即建立模型的算法准确性。10 次交叉验证的打分见式（3），打分总体偏高，原因在于虽然对数据进行了划分，但交叉验证使用的数据集是同一份数据集。

交叉验证结果证明了算法的可行性，但通过交叉验证无法进一步提升模型的精度。通过分析验证集的错误用例可知，预测错误的案例基本都是缺失值填充所在的事故数据，为此对之前的缺失值数据进行重新填充。其中，职业是原始数据中空值最多的特征，采用均值进行填充；年龄不作为一个连续属性值，而是使用一个步长进行离散，变成离散的类目；驾龄的处理方式同年龄；事故原因中的数据合并时，将大量的数据直接划分到“其他”类中，导致“其他”类数据过多，本次处理将数据进一步细化合并，尽量减少“其他”类数据，相同的特征处理有车辆类型、事故形态。因此，对数据进行进一步优化后，再次进行交叉验证，结果有进一步提升。打分均值从0.991 提升至0.995，表明数据的优化有一定的效果。通过混淆矩阵进一步计算召回率已达0.475，对比原始算法有明显提升。

（三）学习曲线

随着训练过程的加深，模型可以使训练结果拟合得越来越好，但也会逐步丧失模型的泛化能力，从而在验证集上产生过拟合问题。为判断使用的逻辑回归模型是否存在过拟合问题，本文计算了另一种形式的学习曲线，将模型的错误率替换成准确率（得分）。使用前文处理过的新能源汽车事故数据进行逻辑回归拟合，得到如图2 所示的学习曲线。为了进一步提升模型的性能，可以继续进行一些特征工程工作，添加一些新的特征或组合特征到模型中来。虽然通过继续生成特征的方式可进一步提升模型性能，但在进行特征分类后的数据维度已经达到65 个，继续增加特征必将提升算法的复杂度。

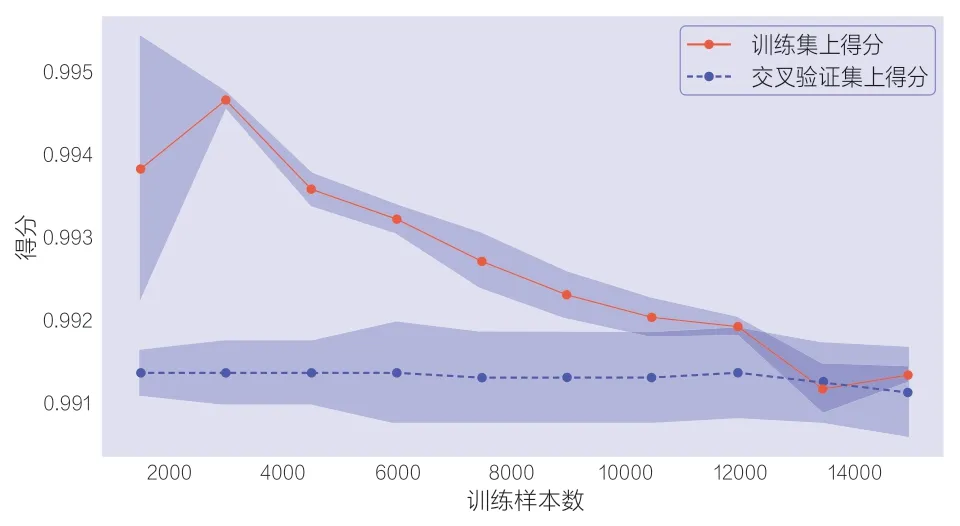
图2 模型学习曲线

三、模型融合

（一）模型融合思路

模型融合是机器学习和数据挖掘在处理数据时最后会用到的工具，对于使用不同分类器算法训练同一份数据集得到的分类器，模型融合将每个分类器分别进行判定，然后对判定结果进行投票统计，将票数最多的结果作为最后的结果，可以较好地缓解训练过程中产生过拟合问题，对结果的准确度有显著提升。本文采用bagging 算法，通过对样本自助采样的方式，使基本学习器存在较大的差异。即对于m 个样本的原始训练集，每次先随机采集一个样本放入采样集，接着把该样本放回，也就是说下次采样时该样本仍有可能被采集到，这样采集m 次，最终可以得到m 个样本的采样集，由于是随机采样，每次的采样集和原始训练集是不同的，和其他采样集也是不同的，这样得到多个不同的弱学习器，如图3 所示。

图3 模型融合思路

（二）模型融合的结合策略

当训练数据过多且数据特征较多时，可通过“学习法”创建其他的学习器来对算法进行融合。其中，stacking 算法具有良好的训练效果。首先，基于初始训练集对模型进行初步的训练，并得出初级学习器；随后，通过对数据的划分“生成”一个新数据集进行训练，得到次级学习器。在这个划分的新数据集中，初级学习器的输出作为次级学习器的输入特征，而初始样本的标记仍被当作样例标记。在此过程中，使用前文提及的交叉验证方法，将初始训练集随机划分为若干个大小相似的集合，每次用部分数据集训练模型，对剩余部分数据产生的预测值作为特征，遍历每一折后，也就得到了新的特征集合，标记还是源数据的标记，用新的特征集合训练一个集合模型，如图4 所示。

图4 模型融合的结合策略

通过上述集成学习中bagging 和stacking 算法的模型融合，对本文使用的逻辑回归模型进行进一步优化，训练的数据集是原始数据集的子集，虽然使用的是同一个分类器算法，但得到的模型却不一样；同时，因没有任何一份子集是全的，因此即使出现过拟合，也是在子训练集上出现过拟合，而不是在全部的数据集上。模型融合后的混淆矩阵和学习曲线分别见表3和图5。

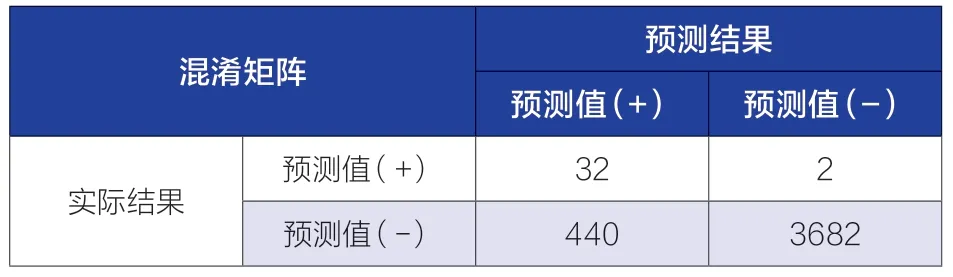
表3 模型融合优化后的混淆矩阵

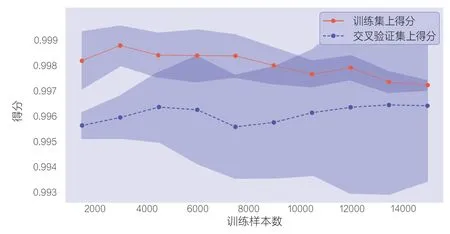
图5 模型融合的学习曲线

从表3 中可以看出，模型预测的真正例（TP）占比已经超过90%、真反例（TN）占比也接近90%、模型精度达到0.893；图5 中的结果表明在进行模型融合后，模型得分进一步提高，过拟合的情况也进一步减少，拟合精度已经处于一个很高的水平。因此，上述模型可以对我国新能源汽车事故中肇事驾驶人的伤害风险进行预测，通过区分不同特征实现对不同车型、道路环境、驾驶人属性等方面的管控，从而有效降低驾驶人在事故中被伤害风险。

四、结论

本文以新能源汽车事故统计数据为切入点，从人、车、路、环境等多个维度分析了多维特征对新能源汽车事故肇事驾驶人伤害风险影响。基于逻辑回归算法，构建了新能源汽车事故驾驶人伤害风险的预测模型，对样本数据进行训练，通过交叉验证的方法来进一步优化对原始数据的处理；通过绘制拟合过程中的学习曲线，验证了逻辑回归算法在新能源汽车事故数据分析中的适用性和准确性；通过集成学习算法的模型融合提升了预测模型的性能，预测准确率达到89.3%。从模型研究中发现，加强对国省道、高速公路上行驶的新能源汽车驾驶人安全监管，是减少新能源汽车交通事故的重中之重；提高新能源汽车安全容错性，是防范肇事驾驶人被伤害的当务之急。