线性自抗扰控制器的改进设计及应用
2023-02-03薛亚丽
张 永, 王 佑, 薛亚丽,3, 李 政,3
(1.国能蚌埠发电有限公司,安徽蚌埠 233411; 2.清华大学 能源与动力工程系,电力系统及发电设备控制和仿真国家重点实验室,北京 100084; 3.清华大学 山西清洁能源研究院,太原 030006)
以火电机组为代表的热力过程普遍存在高阶大惯性系统动态的特点,常规的比例-积分-微分(PID)控制的效果有待提升。随着智能技术的发展,许多学者针对热力过程控制提出了较先进的控制方法。Uddin等[1]基于智能算法设计了神经网络非线性控制结构,并将其应用于锅炉主汽压力控制;陆颖等[2]基于强化学习方法对过热汽温串级控制器进行在线参数整定和优化;Zhang等[3]基于Ⅱ阶Renyi熵准则和神经网络对串级过热汽温系统的外环PID进行训练。但是上述控制系统设计较为复杂,在线计算量较大,较难被应用于分散控制系统中。
由于线性自抗扰控制(ADRC)具有结构简单、整定方便、鲁棒性好及易于现场实现等优点,近年来得到了深入的研究和广泛的应用[4-5]。但对于大惯性大时滞过程,ADRC的快速性不尽人意。为此,有学者提出了不同的改进方法,如文献[6]~文献[8]分别提出了带时滞补偿的自抗扰控制和采用史密斯预估器进行补偿的自抗扰控制,改善了ADRC对高阶时滞对象的控制效果,但仍存在控制量波动较大等问题,一定程度上限制了其在工程上的实际应用。
对于存在高阶惯性或时滞的系统,由于系统输出与输入间的滞后关系,无法将常规反馈控制闭环动态响应设计得过快,否则易产生超调;相比之下,由于系统开环阶跃响应的控制动作可一步到位,无需反复调整,可近似表征系统在反馈控制下闭环能够达到的较快响应过程,因此对于大惯性过程,笔者以被控过程的开环阶跃响应作为预期动态,设计闭环控制系统。
为提高扩张状态观测器(ESO)对大惯性系统的观测效果,可以考虑设计补偿环节,使得被控对象在ESO观测中近似为比例环节,从而使得闭环动态性能与预期动态一致。笔者提出了一种基于模型补偿的自抗扰控制器设计方法,并给出了其参数整定的公式,为该控制器的工程应用提供了参考。
1 自抗扰控制器的改进设计
1.1 线性自抗扰控制原理
笔者在Ⅰ阶线性自抗扰控制器的基础上进行改进设计。为此,可用如下形式描述包含有非线性、内部和外部干扰、参数不确定性的被控过程:
w(t))+bu(t)
(1)
式中:t为时间;y(t)、u(t)分别为被控量和控制量;b为系统增益;g(·)为非线性综合函数,包含了y(t)的各阶导数、外部扰动w(t)和内部扰动d(t)。
定义总和扰动f(t)为:
f(t)=g(·)+(b-b0)u(t)
(2)
式中:b0为b的估计值。
则被控过程(1)可写为:
(3)
假设f(t)是可导的,则可设计Ⅱ阶扩张状态观测器对其进行估计,表达式为:
(4)
式中:z1(t)和z2(t)为ESO的状态量,分别用于对y(t)和f(t)的观测;β1和β2为观测器参数。
设计控制律为:
(5)
式中:kp为控制器参数;r(t)为设定值。
当ESO观测精度较高,且z1→y,z2→f时,将式(5)代入式(3)可得:
(6)
闭环系统近似的预期响应速度可通过kp调整,其预期动态特性表达式为:
(7)
式中:Gcl(s)为闭环预期传递函数;Y(s)和R(s)分别为y(t)和r(t)的拉普拉斯变换;s为复变量。
Ⅰ阶线性ADRC的结构如图1所示。
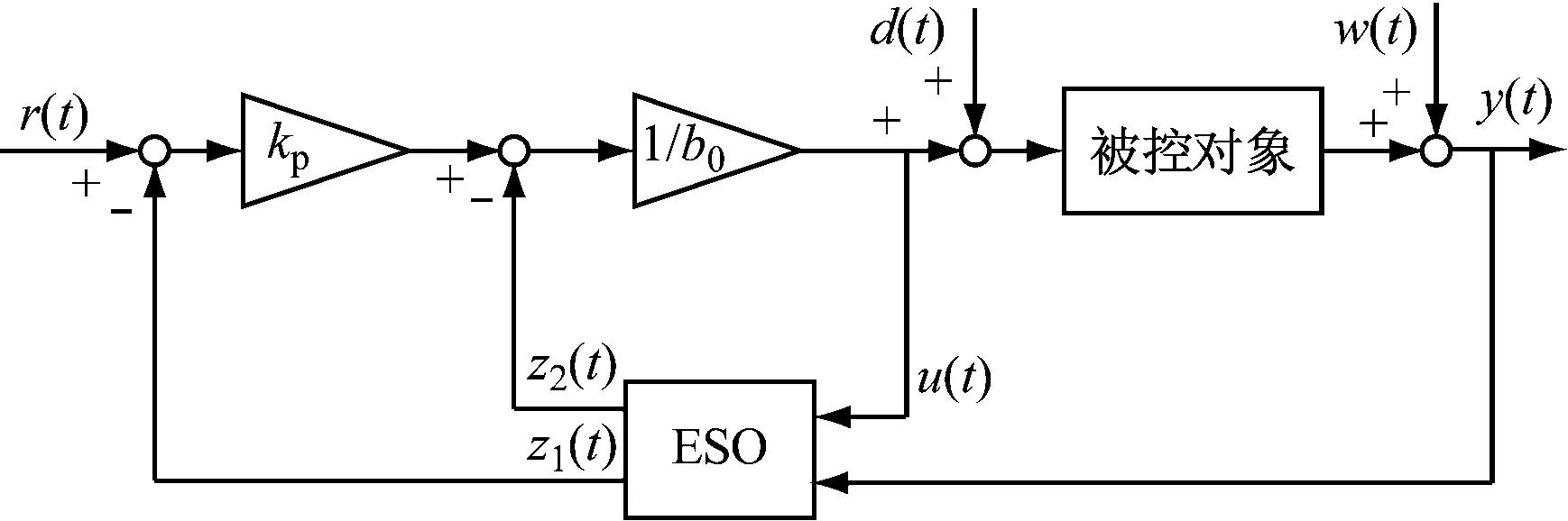
图1 Ⅰ阶线性ADRC结构
其控制器参数kp和扩张状态观测器参数β1、β2可采用带宽参数化[9]的方法整定,即选择控制器带宽ωc和观测器带宽ωo,通过下式计算获得:
(8)
Ⅰ阶线性ADRC的实现形式和参数整定均较为简单,但如果用于大惯性大时滞对象控制,因观测效果不理想,无法获得理想的预期动态特性,存在响应偏慢的问题,因此提出了基于模型信息的改进设计方法。
1.2 自抗扰控制器结构改进
为简化设计和分析,设被控过程近似为n阶惯性环节形式,其传递函数如下:
(9)
式中:G(s)为被控过程的传递函数;K为传递函数增益;T为时间常数;n为系统阶次。
利用此预估模型,设计补偿环节为:
(10)
式中:Gcp(s)为补偿环节的传递函数;Tf为补偿环节的时间常数;m为补偿环节的阶次;Uf(s)和U(s)分别为补偿环节输出uf(t)和输入u(t)的拉普拉斯变换。
含补偿环节的自抗扰控制结构如图2所示。
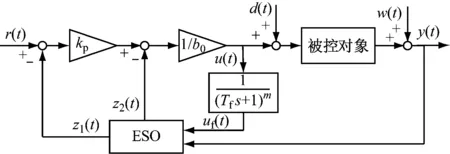
图2 ADRC的改进结构
若取Tf=T,m=n,经补偿后ESO观测的等价系统为:
(11)
即经过补偿后的等价对象是放大系数为K的环节。
此时,ESO可改写为:
(12)
控制律仍采用式(5)的形式。通过选择合理的控制器参数,既可获得近似开环阶跃响应的闭环动态响应,又能兼具抗扰能力和一定的鲁棒性。
1.3 参数整定
在图2所示的补偿结构下,ADRC可调参数为b0、ωc和ωo。以下通过分析给出各参数的选取方法。
1.3.1b0取值
根据式(3)可知,b0表征的是控制作用对系统Ⅰ阶导数增益的估计值,由式(11)可得:
(13)
由式(3)可知,本文ADRC的总和扰动表达式应为:
(14)
对比式(13)与式(14),令:
(15)
为简化整定,可近似取b0=K,误差部分作为总和扰动的一部分,利用ESO进行观测和补偿,即
(16)
1.3.2ωc取值
由式(11)可知,补偿后ESO观测的等效对象传递函数为K,因此控制作用应取比例作用1/K;Ⅰ阶线性ADRC的比例作用可视为ωc/b0,因此ωc的取值应为b0/K;由于b0=K,因此ωc值取为1。
1.3.3ωo取值
ωo的大小反映了观测器对系统状态的跟踪速度;如果ωo过小,观测器对于状态的观测跟踪过慢,使得系统闭环动态响应较慢,且鲁棒性较差;如果ωo过大,会突出高频噪声的影响,造成控制量的不必要动作。因此ωo一般取为10ωc。
综上所述,基于模型补偿的ADRC控制参数可按如下步骤确定:
(1) 获得被控过程的预估模型G(s)=K/(1+Ts)n。
(2) 设计补偿环节Gcp(s)=1/(1+Tfs)m,并取Tf=T,m=n。
本文的ADRC参数整定方法非常简洁,且参数物理意义清晰明确,同时保留了Ⅰ阶线性自抗扰控制器结构简单、易于在工业控制系统上实现的优势,因此具有非常好的工程应用潜力。此外,这种设计方法同样适用于有自平衡能力的非最小相位对象,只需在设计补偿环节时使得ESO观测到的系统为“1”即可。
2 仿真分析
为验证上述控制方法的性能,以文献[10]中某超超临界机组过热汽温惰性区被控过程为例进行仿真分析,传递函数为G(s)=1.202/(27.1s+1)7。
将本文设计的ADRC、按文献[11]整定的ADRC(以下记为LADRC)、基于Skogestad Internal Model Control (SIMC)[12]法整定的PI控制器(以下记为SIMC-PI)及开环控制进行对比,各控制器参数整定结果见表1。

表1 各控制器参数
本文中的开环控制相当于开环响应,仅用于反映被控过程开环阶跃响应的变化快慢,作为动态过程的参照。SIMC-PI是基于Ⅰ阶惯性加纯滞后(FOPTD)模型进行设计的方法,需先将高阶被控过程近似为FOPTD形式,因此先将传递函数近似为Ga(s)=1.21e-87.83s/(103.68s+1),再根据结果整定SIMC-PI的控制参数。
2.1 控制效果对比
采用固定步长为0.1 s进行仿真。设定值阶跃和扰动阶跃下,上述方法的控制效果对比如图3所示。根据仿真结果,通过计算得到的各控制器性能指标见表2,其中σsp和Ts,sp分别为设定值阶跃下的超调量和调节时间,σud和Ts,ud分别为扰动阶跃下的最大动态偏差和调节时间,JIAEsp和JIAEud分别代表设定值阶跃和扰动阶跃下的绝对误差积分指标(2%误差标准)。

(a) 被控量曲线
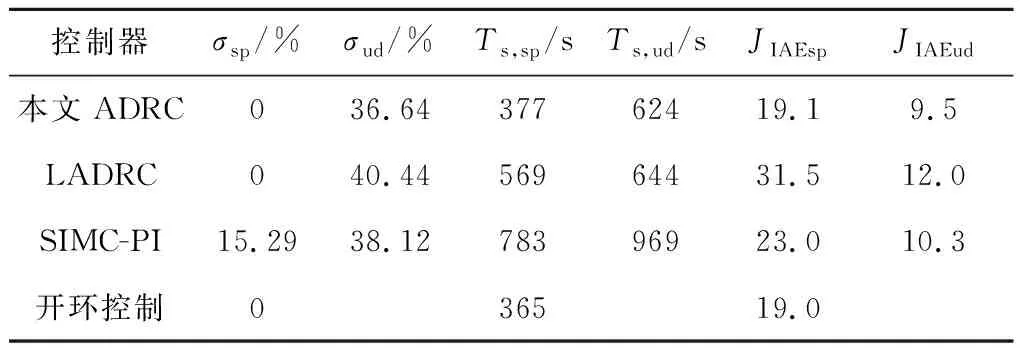
表2 各控制器性能指标
从图3和表2可以得出:(1) 相比于LADRC和SIMC-PI控制器,本文设计的ADRC综合控制性能更好,绝对误差积分指标JIAEsp和JIAEud均为最优,调节时间最快,扰动影响幅值最小且跟踪过程未超调,由此可得,改进设计方法可以改善ADRC的控制效果;(2) 本文设计的ADRC设定值跟踪过程基本与作为参照的开环控制一致,验证了前文理论分析的正确性。
仿真结果表明,当执行机构速率受到限制时,本文设计的ADRC闭环阶跃响应基本与考虑执行机构速率后的开环阶跃响应一致,能达到设计的预期动态。
2.2 鲁棒性能对比
由于被控过程的参数具有不确定性,需要检验所设计控制器的性能鲁棒性。保持控制器参数不变,设被控过程的系统参数T和K在标称值±25%范围内随机变化,服从均匀分布,对各控制器开展Monte Carlo实验。仿真实验重复1 000次,统计各控制器的综合指标JIAEsp和JIAEud,结果如图4所示。性能指标越小表示设定值跟踪和抗干扰性能越好,分布越密集表示性能鲁棒性越强。
由图4可知,在参数不确定性下,ADRC方法和LADRC方法的性能指标变化范围均小于SIMC-PI;其中本文设计的ADRC鲁棒性最好,其设定值跟踪和抗干扰的性能鲁棒性均优于LADRC和SIMC-PI控制器,说明虽然本文设计方法利用了模型信息,但仍具有优良的性能鲁棒性,保证了系统对不确定性的适应能力。
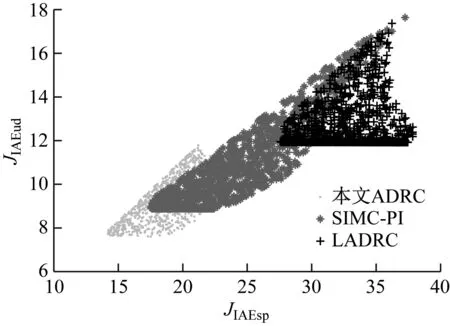
图4 参数不确定性下各控制器的性能指标分布
3 现场应用
根据上述分析和仿真研究,将本文ADRC方法应用于国能蚌埠发电有限公司660 MW二次再热3号机组的1号高压加热器水位和过热汽温Ⅰ级减温喷水控制回路,基于现场集散控制系统(DCS)进行了自抗扰控制器的组态实现、参数整定和控制效果测试。
3.1 高压加热器水位控制
该机组1号高压加热器水位控制回路原有PID调节器参数为kp=0.3,ki=1/130。利用闭环辨识方法获得水位被控过程近似传递函数为G(s)=14.5/(85.3s+1),由此获得本文所提出的自抗扰控制器参数为ωc=1,b0=14.5,ωo=10,Tf=85.1,m=1。
在DCS系统中设置了自抗扰控制器与PID控制器无扰切换逻辑,分别进行了抗扰实验和设定值跟踪实验。
3.1.1 抗扰实验
负荷在620~660 MW范围内波动时,分别将控制方式设置为ADRC控制和PID控制,水位偏差绝对值的最大值JAEmax、平均值JAEave和标准差JAEdev见表3。由表3可知,1号高压加热器水位投入ADRC控制后,最大绝对偏差较原PID控制下降了34.0%,平均绝对偏差下降了40.0%,偏差的标准差下降了40.2%。

表3 高压加热器水位控制偏差对比
负荷扰动下的高压加热器水位变化曲线如图5所示。由图5可知,ADRC控制在负荷波动下的动态偏差更小,显示出良好的抗扰性能。
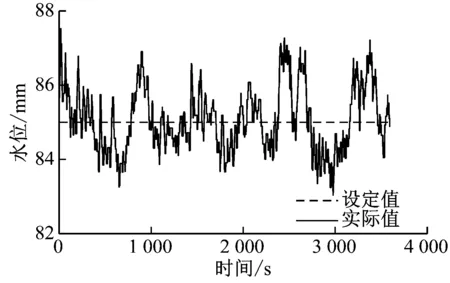
(a) PID控制曲线
3.1.2 设定值跟踪实验
分别在ADRC控制和PID控制方式下,令高压加热器水位设定值发生±5 mm的阶跃变化,实际水位变化曲线如图6所示,超调量和调节时间见表4。与原PID控制器相比,1号高压加热器水位投入ADRC控制后的设定值跟踪下降了78.2%,调节时间缩短了54.4%,显示出良好的设定值跟踪性能。综上可知,本文设计的ADRC控制器对高压加热器水位的控制品质有显著改善。
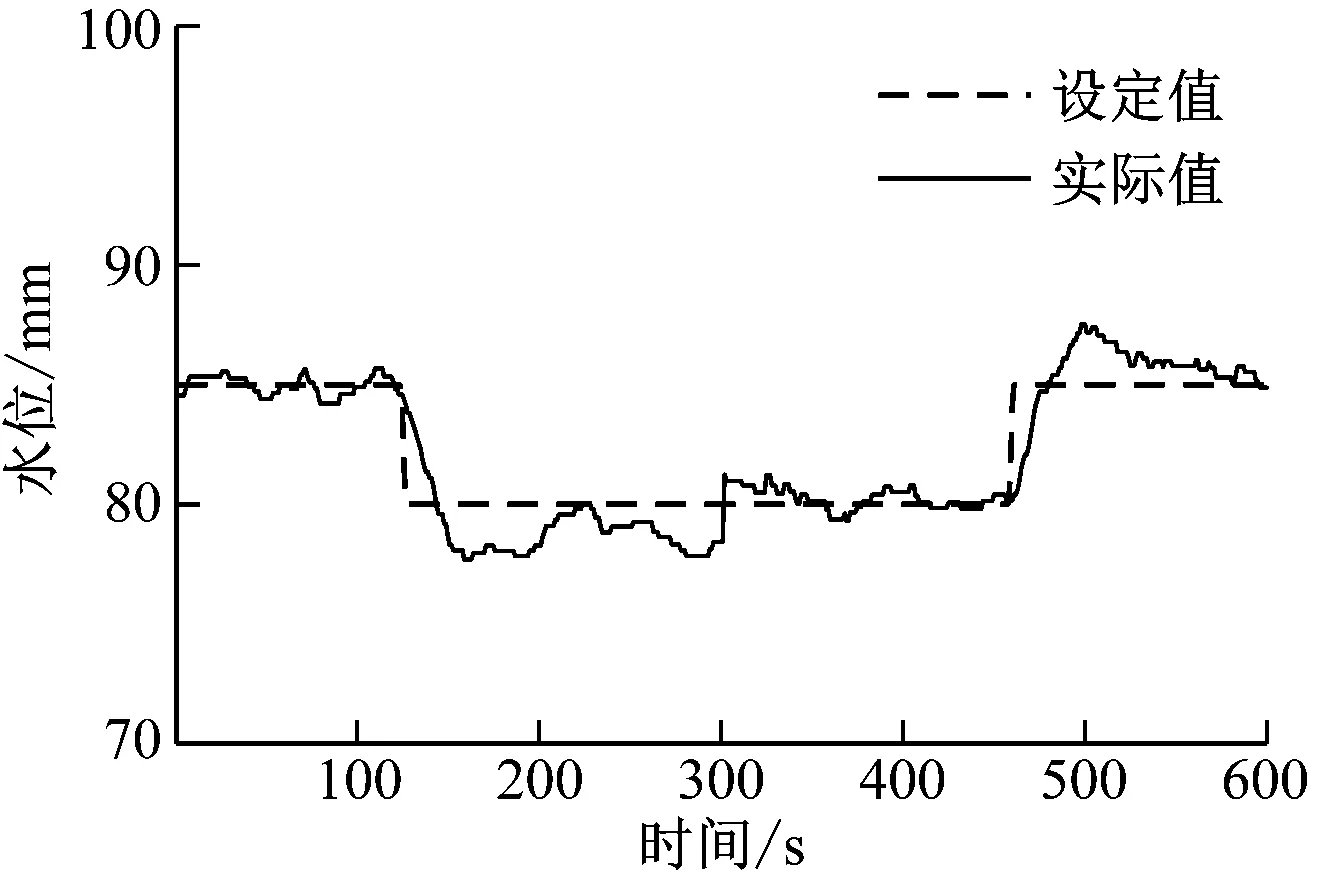
(a) PID控制曲线

表4 高压加热器水位设定值跟踪性能对比
3.2 Ⅰ级过热汽温控制
将本文设计的ADRC应用于该机组B侧过热汽温Ⅰ级喷水减温(即屏式过热器出口汽温)控制,该控制系统采用串级控制结构。考虑到串级控制的外环对应惰性区慢对象,而内环对应导前区快对象,内环的闭环传递函数可近似为1,将外环PID控制器改为ADRC控制器。
根据历史运行数据曲线,估算出外环被控过程可近似为G(s)=0.5/(30s+1)4,通过计算获得ADRC控制器参数为:ωc=1,ωo=10,b0=0.5,Tf=30,m=4。投入ADRC控制系统并运行一段时间后,与历史数据库中工况相似的PID控制进行对比,如图7和图8所示。图7(a)~图7(d)为采用ADRC控制后2021年4月8日的运行曲线,对应负荷变化范围约为600~660 MW;图8(a)~图8(d)为采用PID控制后2021年3月23日的运行曲线,对应的负荷变化范围也为600~660 MW。
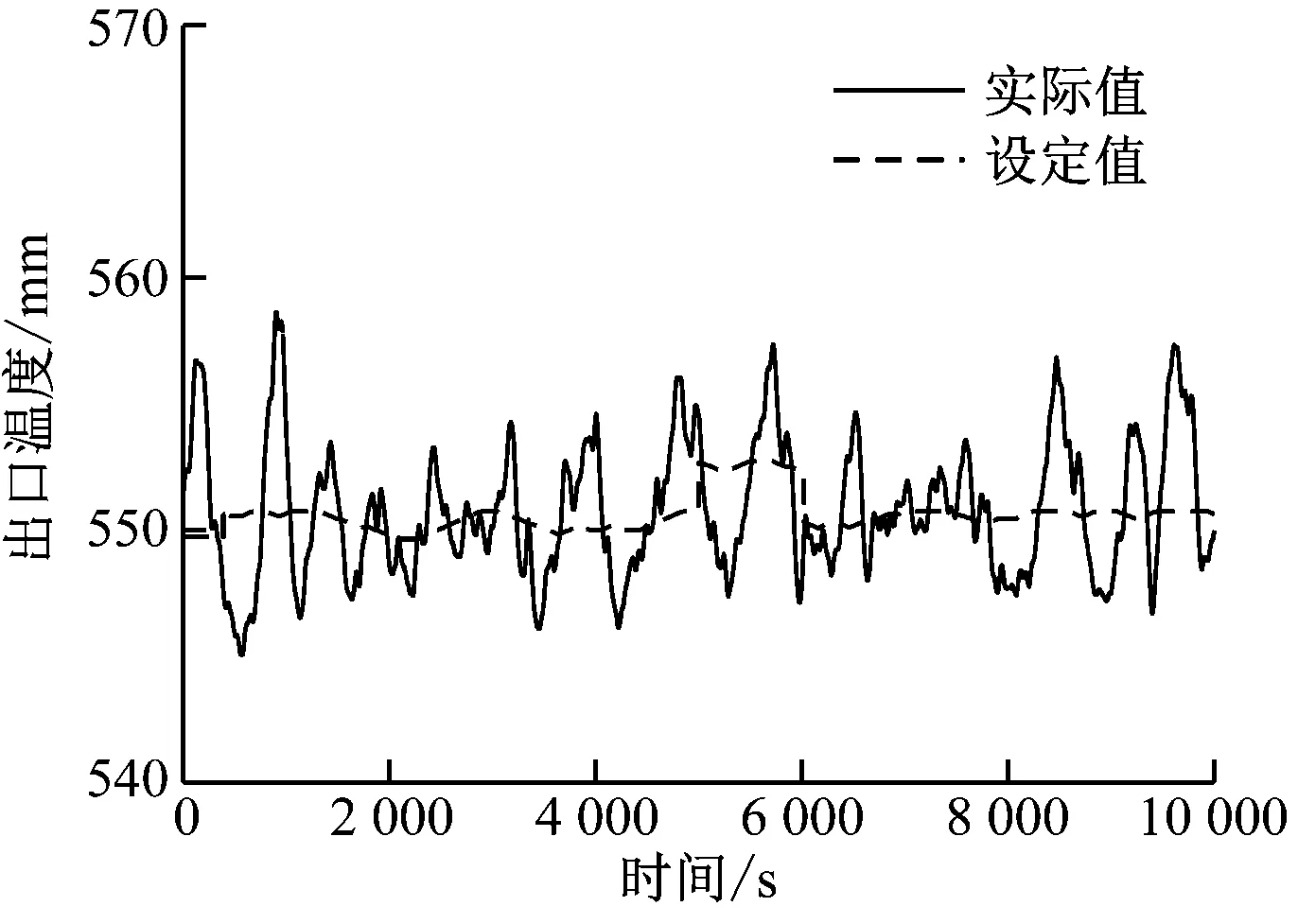
(a) 屏式过热器出口温度
汽温控制偏差绝对值的最大值JAEmax、平均值JAEave和标准差JAEdev见表5。由表5可知,与原PID控制相比,机组B侧Ⅰ级过热汽温投入ADRC控制后的最大偏差下降了56.9%,平均偏差下降了75.6%,偏差的标准差下降了72.5%,该回路的控制品质得到了提高;运行人员手动偏置次数由12次减少为2次,大幅减小了运行人员的压力。
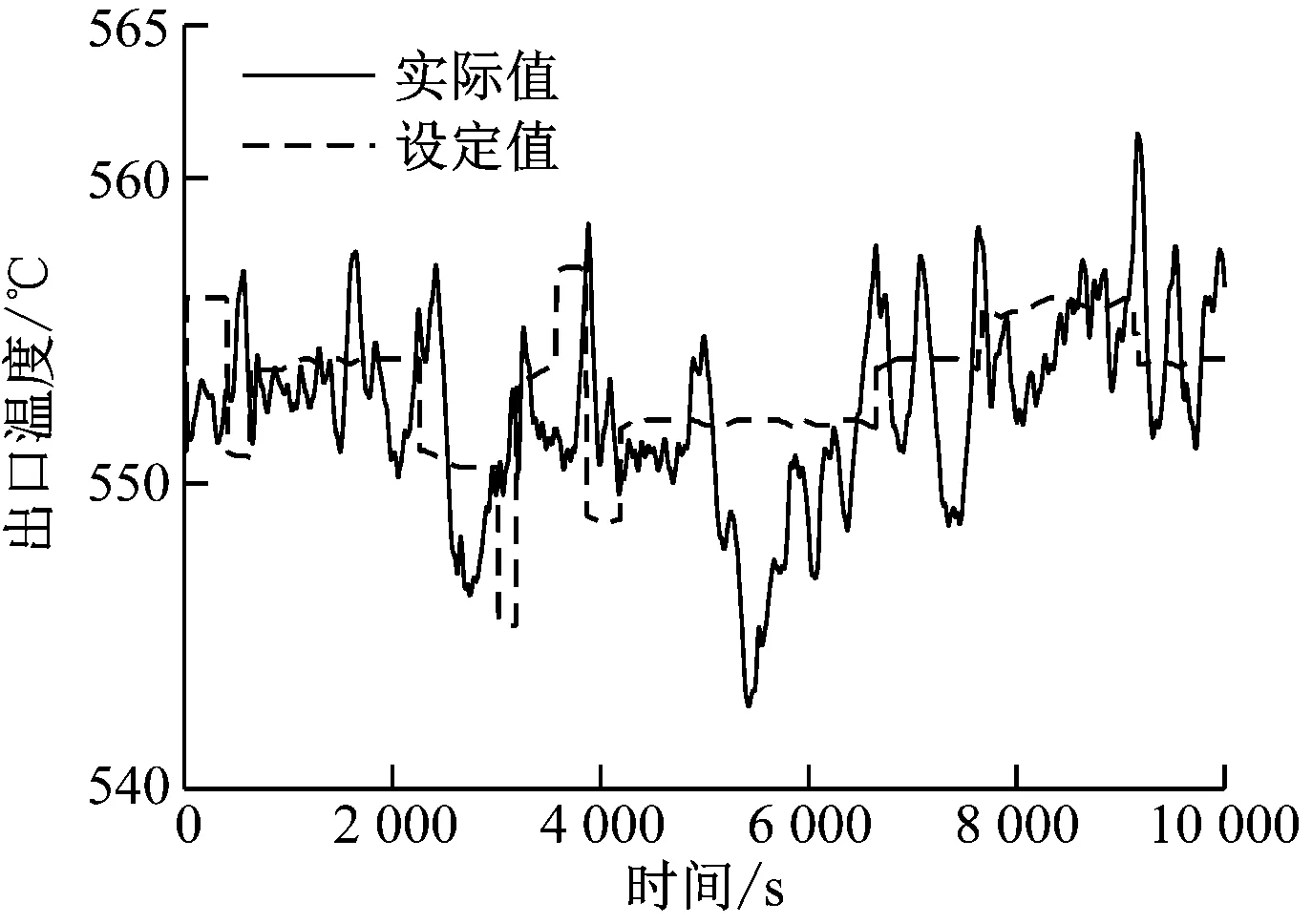
(a) 屏式过热器出口温度
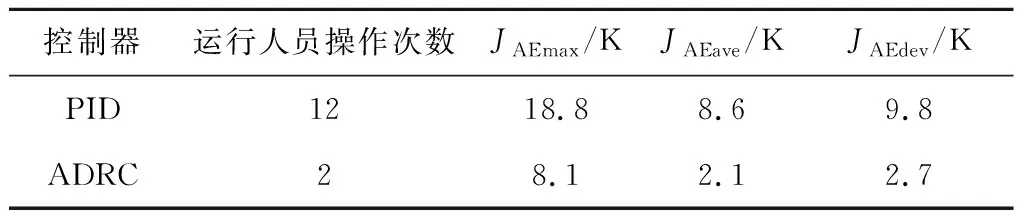
表5 Ⅰ级过热汽温控制偏差对比
4 结 论
针对线性自抗扰控制器应用于热力过程存在大惯性、对象响应偏慢的问题,提出了基于预估模型信息的改进设计方法,并给出了简洁的参数整定公式。仿真结果表明,所设计的自抗扰控制器可以加快闭环系统的动态响应,同时兼具良好的抗扰能力和系统鲁棒性。将本文方法应用于某火电机组高压加热器水位控制和过热汽温控制,现场实验结果表明,相较于原有PID控制器,所设计的控制器改善了系统的控制性能,且其实现和整定简便,具有很好的工程应用潜力。
