考虑岸桥移动的泊位-岸桥容量规划问题研究
2023-02-02嵇玉峰蒋美仙冯佳佳张钰湫郑碧佩
嵇玉峰,蒋美仙,周 健,冯佳佳,张钰湫,郑碧佩
(1.临海市交通投资集团有限公司,浙江 临海 317000;2.浙江工业大学 机械工程学院,浙江 杭州 310023;3.华南理工大学 生物医学科学与工程学院,广东 广州 510641)

综上,已有大量学者对码头的资源容量规划问题进行了研究,其研究对象主要包括泊位、岸桥、锚地以及集卡等码头内重要资源,研究方法主要包括排队论和仿真模拟。在这些研究中,学者们将岸桥和泊位视为一个整体,将其作为排队模型中的一个服务台来看待,各服务台的服务时间相互独立且固定。然而在实际作业过程中,由于岸桥在泊位间的移动,当码头内船舶数量不同时各泊位分配到的岸桥数量也不尽相同,因此其服务能力也随之变化。在该情况下,各泊位的服务能力不再是一个定值,而是和码头内船舶数量息息相关。因此,此时的码头已经变为一个服务时间不定的M/M/C排队模型。若继续使用传统的排队论模型对其进行分析求解,得到的结果势必会产生误差,无法给予码头运营方正确指导。基于此,将泊位与岸桥作为单独的个体加以考虑,同时又提出使用最大服务能力规则来确定岸桥数量、船舶数量以及泊位服务能力之间的关系,并根据此规则得到码头系统稳态下的状态转移图以及平衡方程,从而求得船舶等待队长、等待时间等性能指标,并将这些指标应用至规划模型中。
1 泊位-岸桥容量规划模型建立
1.1 模型假设与符号说明
将集装箱码头内的船舶排队过程抽象成一个M/M/C排队模型,同时为了便于研究所建模型,依据集装箱码头的实际情况和排队论模型的特点,提出以下几点假设:1) 模型中考虑的码头为离散型码头,即码头的岸线被平等划分为若干个泊位,每个泊位一次只能容纳一艘船舶;2) 码头内各岸桥拥有相同的工作能力,且不考虑多台岸桥同时为一艘船舶服务时可能存在的作业效率影响;3) 为了使船舶靠泊于泊位后能立即得到岸桥服务,故规定无论是否空闲,各泊位都必须至少配置2台岸桥;4) 考虑到泊位存在长度限制,且岸桥需要具备独立的作业空间,故各泊位理论上存在最大可配置岸桥数量,规定各泊位至多能同时存在4台岸桥;5) 岸桥只能在轨道上移动,从而实现泊位内不同的岸桥配置,且岸桥之间不能交叉移动;6) 不考虑船舶的优先级,根据先到先服务的原则进行服务。
为了提高文章的可读性和简洁性,对后续需要用到的符号作出定义(表1)。

表1 符号定义表Table 1 Symbol definition table
船舶在集装箱码头的服务过程如图1所示。船舶到港后,码头方会判断此时岸线上是否存在空闲泊位:若存在,则令到港船舶靠泊在空闲泊位上,并根据可用岸桥数量为其安排岸桥进行装卸服务;若不存在,则需判断锚地是否可以让其停留等待,若可以,则令船舶在锚地等待,直到出现空闲泊位。就锚地而言,由于码头外一般存在广阔的海域,因此没有空闲泊位停靠的船舶可以在海上等待,即假设锚地容量为无限,故此容量规划模型的研究对象仅为泊位和岸桥资源。

图1 集装箱码头服务排队系统工作流程示意图Fig.1 Work flow of container terminal service queuing system
1.2 集装箱码头服务系统分析
根据集装箱码头作业流程,可以发现船舶在码头的作业流程与一个拥有多服务台的服务系统十分相似。船舶即为这个服务系统的顾客,各泊位即为该服务系统的服务台,而各服务台的服务效率则与岸桥数量相关,锚地则相当于服务系统的队列。毫无疑问,这是一个M/M/B+Ba/∞形式的多服务台排队系统。与一般的服务系统不同,由于各泊位可以共享岸线上的岸桥,因此随着该码头系统内船舶数量的变化,各个泊位的服务效率也在发生变化。根据假设3,4,不管是否有船舶停靠,每个泊位都必须配置至少2台,至多4台岸桥,因此各泊位的服务能力只能为2μq,3μq或4μq。而整个码头服务系统的服务能力则与系统内船舶数量相关,这一规律可定义为最大服务能力规则(Maximum service capacity rule,MSCR)。通过这一规则,可以使船舶在以最大服务能力接受服务的基础上为各泊位分配岸桥,从而提高码头整体的服务效率,即
(1)
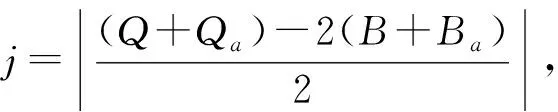
为了便于理解MSCR,以一个拥有5个泊位、13台岸桥的集装箱港口为例对其进行说明。首先,因为规定了每个泊位必须配置最少2台岸桥,所以能够在各泊位间自由分配的岸桥数为3台。如表2所示,当有一艘船舶到港时,其停靠于泊位1,根据MSCR,为了使其能以尽可能大的服务能力进行装卸,需要将可自由分配的2台岸桥分配给该泊位,此时该泊位的服务能力为4μq,可自由分配岸桥数为1台。当又有一艘船舶到港后,使其靠泊于泊位2,同理将可自由分配的岸桥分配给该船,此时泊位1和泊位2的服务能力分别为4μq和3μq,此时可自由分配岸桥数为0。因此当后续船舶到港后,除非有船舶离港,即泊位空闲,否则后续船舶都无法分配到多余的岸桥,故这些泊位的服务能力均为2μq。

表2 码头内的船舶数与码头服务能力值对应表Table 2 Correspondence between the number of ships in the terminal and the service capacity value of the terminal
根据此案例可以发现整个码头的服务能力与该码头内船舶数量之间的关系。依此类推,对一个初始拥有B个泊位、Q台岸桥,拟新建Ba个泊位、Qa台岸桥的集装箱码头而言,该码头服务系统的状态变换关系图如图2所示,状态s(s=1,2,…)代表系统内有s艘船舶。从状态s到状态s+1表示码头服务系统中有一艘船舶抵港,而从状态s到状态s-1表示码头服务系统中有一艘船舶离港。当码头服务系统中的船舶数为0≤s≤j时,所有船舶都能以最大服务能力4μq进行装卸作业,其余的B+Ba-s个泊位处于空闲状态;当码头服务系统中的船舶数为j+1≤s≤B+Ba时,有j个泊位以最大服务能力4μq进行装卸作业,第j+1个泊位以服务能力3μq或2μq进行装卸作业,剩下s-j-1个泊位以最小服务能力2μq进行装卸作业,其余的B+Ba-s个泊位处于空闲状态;当码头服务系统中的船舶数为s>B+Ba时,码头内所有岸桥都处于工作状态,码头服务系统以最大服务能力(Q+Qa)μq为船舶提供服务,s-(B+Ba)艘船舶在锚地停泊等待接受服务。

图2 码头服务系统排队过程状态转移图Fig.2 The state transition diagram of the queuing process of the terminal service system
根据图2可以得到码头服务系统处于稳定状态时的状态转移方程,即
λPs-1=4sμqPs1≤s≤j
(2)
λPs-1=[(Q+Qa)-2(B+Ba-s)]μqPs
j+1≤s≤B+Ba
(3)
λPs-1=(Q+Qa)μqPss>B+Ba
(4)
递归可以得到任意状态的概率Ps为
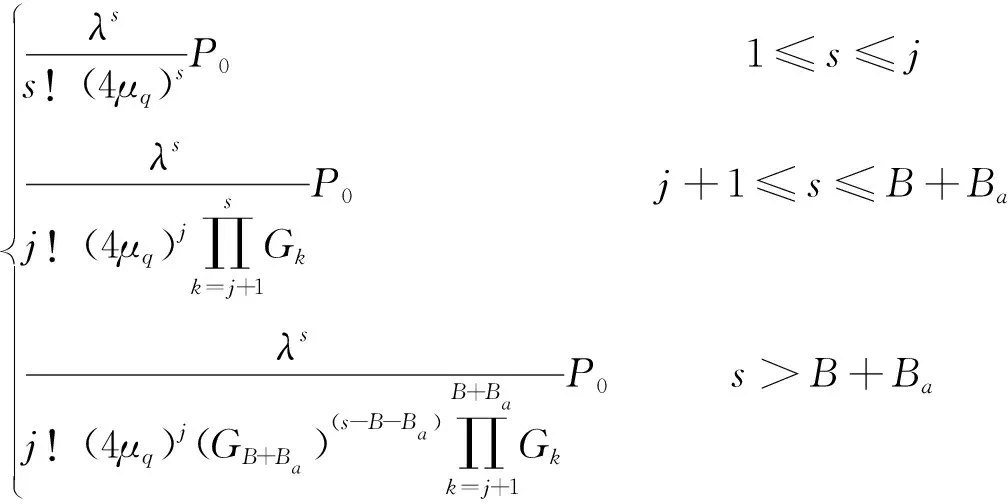
(5)

D1P0+D2P0+D3P0=1
(6)
其中:
(7)
(8)
(9)
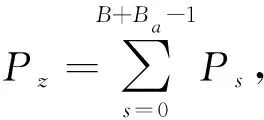
(10)
(11)
(12)
(13)
同理根据码头服务系统排队过程状态转移图可以得到状态转移方程为
λPs-1=4sμqPs1≤s≤B+Ba
(14)
λPs-1=(Q+Qa)μqPss>B+Ba
(15)
根据状态转移方程,可以得到任意状态的概率Ps为

(16)
其中:
(17)
(18)
此时船舶即到即靠率、等待船舶平均队长以及船舶平均队长分别为
(19)
(20)
(21)
将Lq,L代入下文的目标函数中即可得到不同泊位岸桥容量下的码头服务系统总费用。
1.3 泊位-岸桥容量规划模型建模
以码头的每日总运营成本最小为目标函数建立泊位-岸桥容量规划模型。对于码头需要新增建设的泊位和岸桥,在规划时需考虑其建设成本;同时,当这些新增资源投入运营后,需考虑码头为船舶提供服务的成本。因此,码头每日的运营总成本包括新增泊位和岸桥的分摊每日固定成本、船舶等待成本、作业成本以及码头空闲时的损失成本。与此同时,码头运营者对码头的服务强度以及顾客的满意度也有一些指标上的要求,而受地理环境的影响,码头也不可能无限制地建设泊位。假设新增泊位数为Ba,新增岸桥数为Qa,码头服务系统中每日等待船舶平均队长为Lq,平均每日空闲时间为W,则泊位岸桥容量规划模型为
minF(Ba,Qa)=CsLq+CvLm+CbBa+CqQa+CtW
(22)
(23)
(24)
2(B+Ba)≤Q+Qa≤4(B+Ba)
(25)
B+Ba≤Bmax
(26)
Ba,Qa∈N
(27)
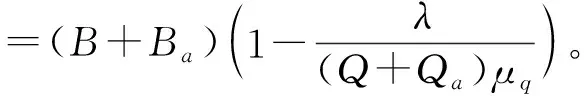
2 模拟迭代算法设计
泊位岸桥容量规划模型是一个复杂的非线性离散规划模型,因此很难从模型中直接得到一个解析解。受码头地理资源的限制,码头可容纳泊位数量十分有限,可行解空间不大。因此通过设计一种模拟迭代算法,以现有泊位岸桥容量为初始解,不断更新泊位和岸桥的数量并计算目标函数值F(Ba+Qa),从而得到最优解。受决策变量和可行解空间的性质影响,决策变量的迭代步长为1,这样算法可以搜索到路径上的所有整数可行解,有效提高了搜索效率并避免非正整数可行解的产生。
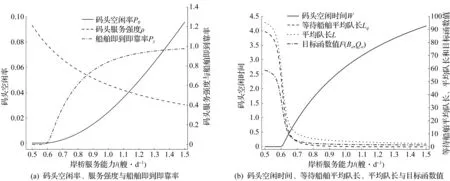
模拟迭代算法的求解过程如图3所示,具体如下:1) 令新增泊位数Ba=0、新增泊位数Qa=0,目标函数最优值MinF(Ba,Qa)=+∞;2) 计算等待船舶平均队长Lq、作业船舶平均队长Lm、码头服务系统空闲时间W、船舶即到即靠率Pz、码头服务强度系数ρ以及码头每日运营总成本F(Ba,Qa);3) 判断船舶即到即靠率Pz与码头服务强度系数ρ是否满足码头方的指标要求,若ρ≥β,Pz≥α,且F(Ba,Qa) 图3 模拟迭代算法求解流程图Fig.3 Simulated iterative algorithm solution flow char 通过一个实际集装箱码头的案例来验证模型和算法的有效性。该码头共有7个泊位,15台岸桥。以天为单位时间,根据码头提供的历史船期表,统计该码头每日到达的船舶数量。表3列举了该集装箱码头2020年的每日船舶到达数量。 表3 某集装箱码头2020年的每日船舶到达情况Table 3 Number of vessel arrivals per day for a container terminal in 2020 根据表3可得到如图4所示的船舶到达频数分布图。图4中横坐标表示该码头每日到港的船舶数量,纵坐标表示天数。由图4可知:集装箱码头每日船舶到达数量的分布规律特征基本符合Poisson分布的特征。 图4 船舶到达频数分布图Fig.4 The frequency distribution of the container vessel arriving at the terminal 为确定该集装箱码头船舶的每日到港规律,通过卡方检验对表3中的统计数据进行拟合分析,可以发现该码头每日船舶到达数量服从λ=9.10的泊松分布。同样的,通过对该码头2020年服务的3 301艘船舶的在港时间进行统计分析,可以发现船舶在该码头内的在港时间分布规律如图5所示。图5中横坐标表示船舶的在港时间,纵坐标表示在港时间为x-1~x的船舶数量。 图5 船舶在港时间频数分布图Fig.5 The frequency distribution of the container vessel time in port 由文献[17]可知:单位船舶在码头内的每日作业成本Cv为32元,新增单个泊位的分摊每日固定成本Cb为6.1元,新增单台岸桥的分摊每日固定成本Cq为1.1元,单位船舶等待服务的每日等待成本Cs为64元,码头空闲的每日单位成本Ct为15元。 通过将结果与传统的排队论进行对比分析来验证模型和方法的有效性。传统的排队论方法将这两者视作一个整体,因此各泊位的服务强度均相等,即 (28) 根据式(28),可以得到如图6所示的状态转移图,状态k(k=1,2,…)代表系统内有k艘船舶。从状态k到状态k+1表示码头服务系统中有一艘船舶抵港,而从状态k到状态k-1表示码头服务系统中有一艘船舶离港。当码头服务系统中的船舶数为0≤k≤B+Ba时,所有船舶均以相同的服务能力μ进行装卸作业,其余的B+Ba-k个泊位处于空闲状态;当码头服务系统中的船舶数为k>B+Ba时,码头内所有泊位都处于工作状态,码头服务系统以最大服务能力(B+Ba)μ为船舶提供服务,剩下k-(B+Ba)艘船舶在锚地停泊等待接受服务。 图6 排队论下的码头系统状态转移图Fig.6 State transition diagram of the terminal system under queuing theory 据此,系统内有k艘船舶的状态概率为 (29) 船舶即到即靠率、等待船舶平均队长以及船舶平均队长为 (30) (31) (32) 式中 分别按传统的排队论方法和笔者所提的应用MSCR规则的排队论方法对该集装箱码头的容量配置规划模型进行求解。计算得到的在现有船舶到港率下该码头的最佳泊位岸桥容量以及规划前后码头的各项服务指标如表4和图7所示。 表4 传统排队论方法和MSCR规则下的排队论方法规划结果对比Table 4 Comparison of results planning by applying traditional queuing theory and queuing theory under the MSCR rule 图7 传统排队论方法和MSCR规则下的排队论方法规划指标比较Fig.7 Comparison of indicators planning by applying traditional queuing theory and queuing theory under the MSCR rule 该集装箱码头规划前、使用传统排队论方法以及应用MSCR规则的排队论方法规划后的码头空闲率、服务强度、队列长度以及运营费用等指标之间的比较如图7所示。由表4及图7可知:对于该集装箱码头而言,现有的泊位数量虽然可满足目前的到港船舶数量,但岸桥数量较为缺乏,这使得该码头为船舶提供服务的时间变长,也就导致服务强度虽高,但码头空闲率、空闲时间与船舶即到即靠率3项指标都偏低,造成了船舶在该码头的平均等待队长与服务队长都较高,因此码头的总费用也居高不下。而据规划结果可知:当该码头在当前容量基础上新增7台岸桥后,该码头的船舶即到即靠率可提高86.92%,平均等待队长和平均队长可分别减少6.06艘和8.6艘,然而码头的服务强度也会有所降低,码头的空闲率和空闲时间分别增加2.86%和2泊位·d。从总费用来说,在新容量配置下该码头的每日运营总费用能够减少43 175.38元,约为原来的60%。 通过应用MSCR规则的排队论方法与传统排队论方法所得结果的比较,可发现两者对该码头的泊位与岸桥容量规划的指导结果是一致的,有效验证了笔者所提方法的可行性。与此同时,相较于传统排队论方法,应用MSCR规则的排队论方法能够给码头带来更高的码头空闲率和顾客满意度以及更低的等待船舶队长和运营总费用。这使得该码头能为更多的船舶提供服务,也更具竞争力。 为了更全面地从泊位岸桥容量规划模型中获取信息,从而为集装箱码头管理者提供更有价值的投资决策与管理方法,针对集装箱码头的平均每日船舶到达数量λ、岸桥服务能力μq及泊位岸桥容量(Ba,Qa)分别作敏感性分析。选用码头空闲率P0、码头服务强度ρ、船舶即到即靠率Pz、平均每日码头空闲时间W、每日等待船舶平均队长Lq、每日船舶平均队长L以及码头每日总费用F(Ba,Qa)作为敏感性分析指标。 在当前泊位岸桥容量配置下,每日船舶到达数量对码头空闲率、平均队长等敏感性指标的影响如图8所示。由图8(a)可知:集装箱码头平均每日船舶到达数量λ的变动范围为[6,12]。就码头空闲率P0以及船舶即到即靠率Pz而言,当λ为[6,10]时,P0和Pz都会随着λ的增长而快速下降;而当λ在[10,12]内增长时,P0和Pz则趋近于0,且没有变化,这是因为当λ增长到一定程度而岸桥作业效率又没有变化时,码头内总是有船舶在接受服务,因此码头内没有船舶的概率以及船舶即到即靠的概率都接近于0。就码头的服务强度ρ而言,其变化趋势与λ呈线性递增关系。由图8(b)可知:就每日等待船舶平均队长Lq、每日平均队长L而言,当λ为[6.0,9.5]时,Lq与L随λ变化的趋势并不明显,这是由于当λ在[6.0,9.5]内增长时,由于码头内岸桥服务能力溢出,船舶到港后能在较短时间内完成装卸,因此λ的增长并不能使Lq和L快速增长;但当λ为[9.5,11.0]时,码头内岸桥服务能力开始出现不足,故Lq与L又会随着λ的增长而迅速增长;当λ为[11,12]时,Lq与L随着λ增长而增长的趋势也逐渐平缓。对平均每日码头空闲时间W来说,W与λ呈线性递减关系。而码头总费用F(Ba,Qa)的变化趋势与Lq和L的变化趋势基本一致。当λ为[6.0,9.5]时,码头总费用的变化不大,而当λ为[9.5,11.0]时,码头总费用则会随着λ的增加而迅速增长,当λ为[11,12]时,F(Ba,Qa)随着λ增长而增长的趋势也逐渐平缓。因此,根据图8,针对该码头当前容量配置而言,其平均每日船舶到达数量λ控制在8~9艘为宜。 图8 平均每日船舶到达速率的敏感性分析Fig.8 Sensitivity analysis of average daily ship arrival rate 在当前泊位岸桥容量配置下不同岸桥服务能力对码头空闲率、平均队长等敏感性指标的影响如图9所示。由图9(a)可知:岸桥的服务能力μq变动区间为[0.5,1.5]。就码头空闲率P0而言,当μq在[0.5,0.7]内变动时,P0趋近于0,且变化不大,这是因为此时岸桥服务能力虽然增长了,但依然无法满足到港的船舶数量,因此μq的增长无法让P0得到提升;但当μq超过0.7艘/d后,岸桥服务能力逐渐超过船舶到港数量后,船舶在码头内的停留时间得以减少,因此P0便随着μq的增长而快速增长。就船舶即到即靠率Pz而言,当μq为[0.5,0.6]时,Pz趋近于0,且变化不大,同样的道理,此时岸桥服务能力的增长无法有效减少码头内船舶的数量,因此Pz也近乎为0;而当μq在[0.6,1.0]内增长时,岸桥服务能力超过船舶到港数量后,码头内船舶数也逐渐减少,因此Pz便随着μq的增长而快速增长;但当μq超过1.0艘/d后,Pz的增长趋势逐渐减缓,并趋近于1。就码头的服务强度ρ而言,其随着μq的增长而逐渐降低。由图9(b)可知:就平均每日等待船舶平均队长Lq、每日平均队长L而言,当μq为[0.50,0.55]时,Lq与L随μq变化的趋势并不明显,这是由于此时码头内岸桥服务能力不足,船舶到港后无法及时装卸,因此Lq与L居高不下;当μq为[0.55,0.70]时,码头内岸桥服务能力逐渐增长,故Lq与L随着μq的增长而迅速减少;当μq超过0.7艘/d后,Lq与L随着μq增长而降低的趋势逐渐平缓。对平均每日码头空闲时间W而言,W与μq呈线性递增关系。而码头总费用F(Ba,Qa)的变化趋势与Lq和L的变化趋势基本一致。当μq为[0.50,0.55]时,码头总费用的变化不大,而当μq为[0.55,0.70]时,码头总费用则会随着μq的增加而迅速下降,当λ为[0.7,1.5]时,F(Ba,Qa)随着μq增长而降低的趋势也逐渐平缓。因此,根据图9,针对该码头当前容量配置而言,其岸桥服务能力μq控制在0.8~0.9艘/d为宜。 图9 岸桥服务能力的敏感性分析Fig.9 Sensitivity analysis of quay crane service capacity 为了探索泊位岸桥容量对码头空闲率P0、码头服务强度ρ、船舶即到即靠率Pz、每日等待船舶平均队长Lq、每日船舶平均队长L、平均每日码头空闲时间W以及码头服务系统平均每日总费用F(Ba,Qa)的影响,设置的码头泊位岸桥容量如表5所示。当泊位数为6~9时各敏感性指标随岸桥数量的变化曲线如图10~13所示。 表5 泊位-岸桥容量取值范围Table 5 Value range of berth-quay crane capacity 图10 泊位-岸桥容量的敏感性分析(泊位数为6)Fig.10 Sensitivity analysis of berth quay crane capacity (the number of berths is 6) 图11 泊位-岸桥容量的敏感性分析(泊位数为7)Fig.11 Sensitivity analysis of berth quay crane capacity (the number of berths is 7) 图12 泊位-岸桥容量的敏感性分析(泊位数为8)Fig.12 Sensitivity analysis of berth quay crane capacity (the number of berths is 8) 图13 泊位-岸桥容量的敏感性分析(泊位数为9)Fig.13 Sensitivity analysis of berth quay crane capacity (the number of berths is 9) 由图10~13可知:在不同的泊位数情况下,P0,ρ,Pz,Lq,L,W6个指标随岸桥数量变化而变化的趋势基本一致。其中,P0,Pz,W随着岸桥数量的增长而逐渐增长,不同的是P0与Pz的增速逐渐趋近于0,而W与岸桥数量之间则近似于线性递增关系;ρ,Lq,L均随着岸桥数量的增长而逐渐下降,Lq和L的增速随着岸桥数量的递增而逐渐减小并趋近于0,而ρ与岸桥数量之间则近似于线性递减关系。 就码头总费用F(Ba,Qa)而言,当码头泊位数为6时,F(Ba,Qa)呈现出了单调递减的变化趋势;而当码头泊位数为7,8或9时,F(Ba,Qa)则呈现出了先单调递减后单调递增的变化趋势,其拐点分别出现在岸桥数为26(泊位数为7)、26(泊位数为8)和28(泊位数为9)时。不难发现,泊位岸桥容量存在一个能使F(Ba,Qa)达到最小值的恰当值。由图9~12可知:在使码头系统的服务强度系数ρ以及船舶即到即靠率Pz不小于0.6的前提条件下,泊位数为6、岸桥数为22时(图10),F(Ba,Qa)达到了最小值,此时F(Ba,Qa)为164.28,码头系统的服务强度系数ρ为0.61,船舶即到即靠率Pz为82.6%。 针对岸桥在泊位间的移动使得各泊位服务能力变化这一现实情况,根据码头服务能力与码头系统内船舶数量间的关系提出了码头最大服务能力原则,并据此对船舶在码头内的服务过程进行分析。为了对集装箱码头的泊位岸桥容量规划问题进行研究,将码头服务系统抽象成多服务台排队系统,以码头每日总运营成本最小为目标构建了一个描述该问题的非线性整数规划模型。通过实际案例的应用,验证了模型的有效性,并为码头确定了最佳泊位与岸桥数量配置。此外,还分别就平均每日船舶到达数量λ、岸桥的服务能力μq及泊位-岸桥容量(Ba,Qa)进行了敏感性分析,从而更加深入地洞察集装箱码头的效益问题,为码头的管理和未来发展战略提供理论支撑。目前对集装箱码头泊位岸桥容量配置的研究虽然有了一定的进展,但由于集装箱码头是一个复杂的物流系统,仍有一些不足之处需要通过研究改进。在实际码头生产作业中,现在的集装箱船一般都有船期表,对到港和离港时间都有一定要求,因此船舶在码头内不可能无限等待,即码头系统的队长存在一定的限制,这可以作为后续新的研究方向。此外,除了泊位和岸桥,集卡、堆场和锚地等码头内资源对码头的竞争力也有着不可忽视的影响,因此后续研究可以将更多的重要资源考虑进模型中。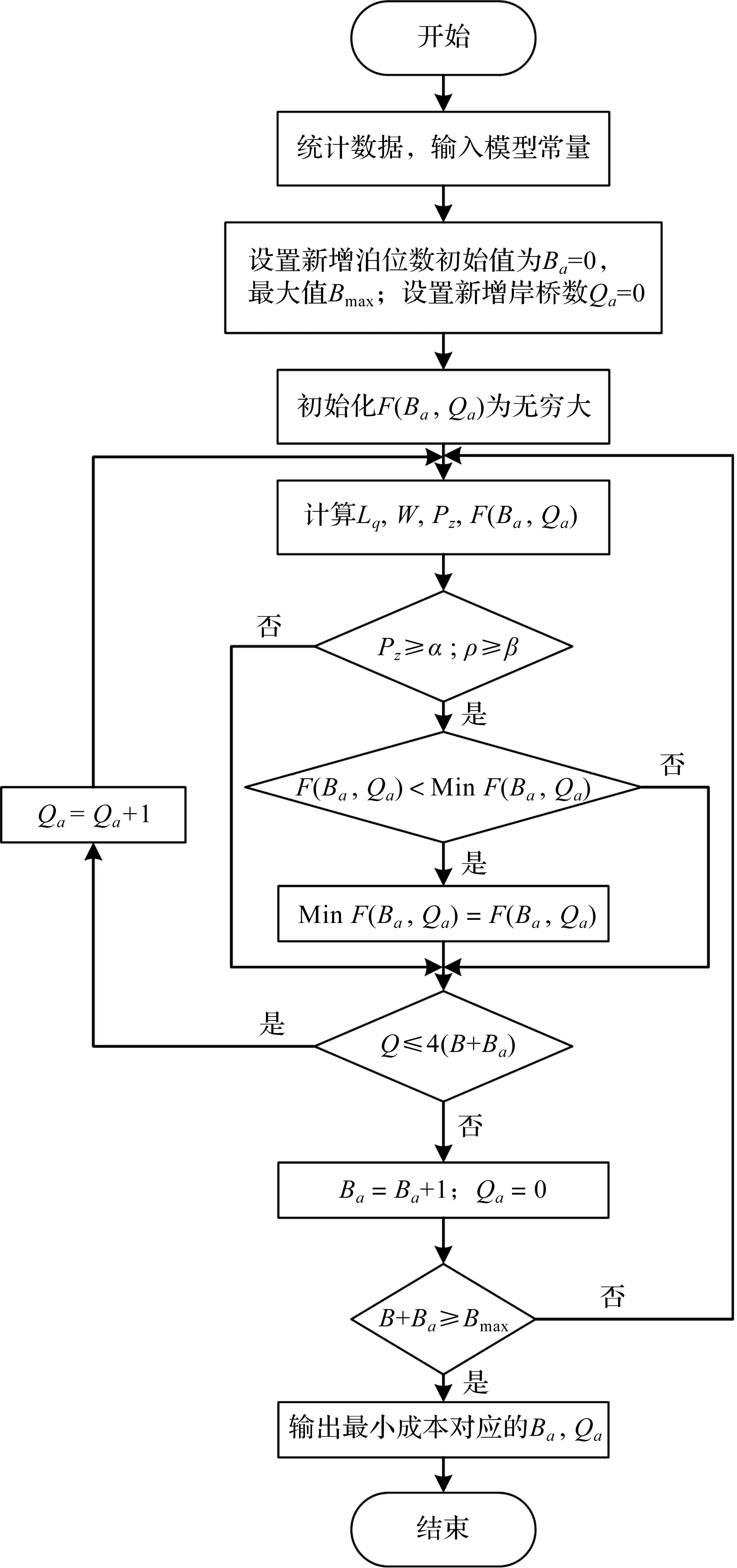
3 案例应用
3.1 码头现状分析
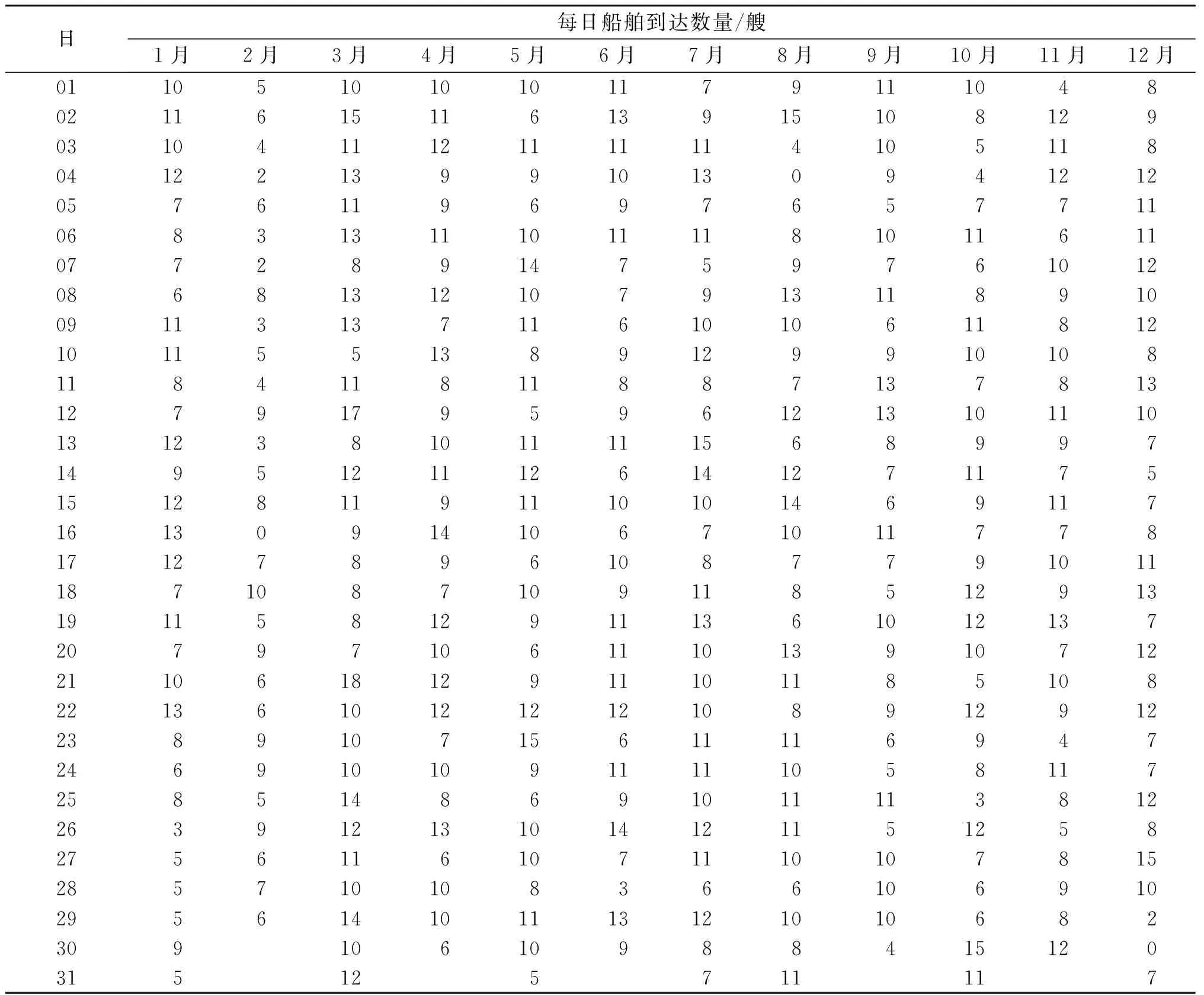
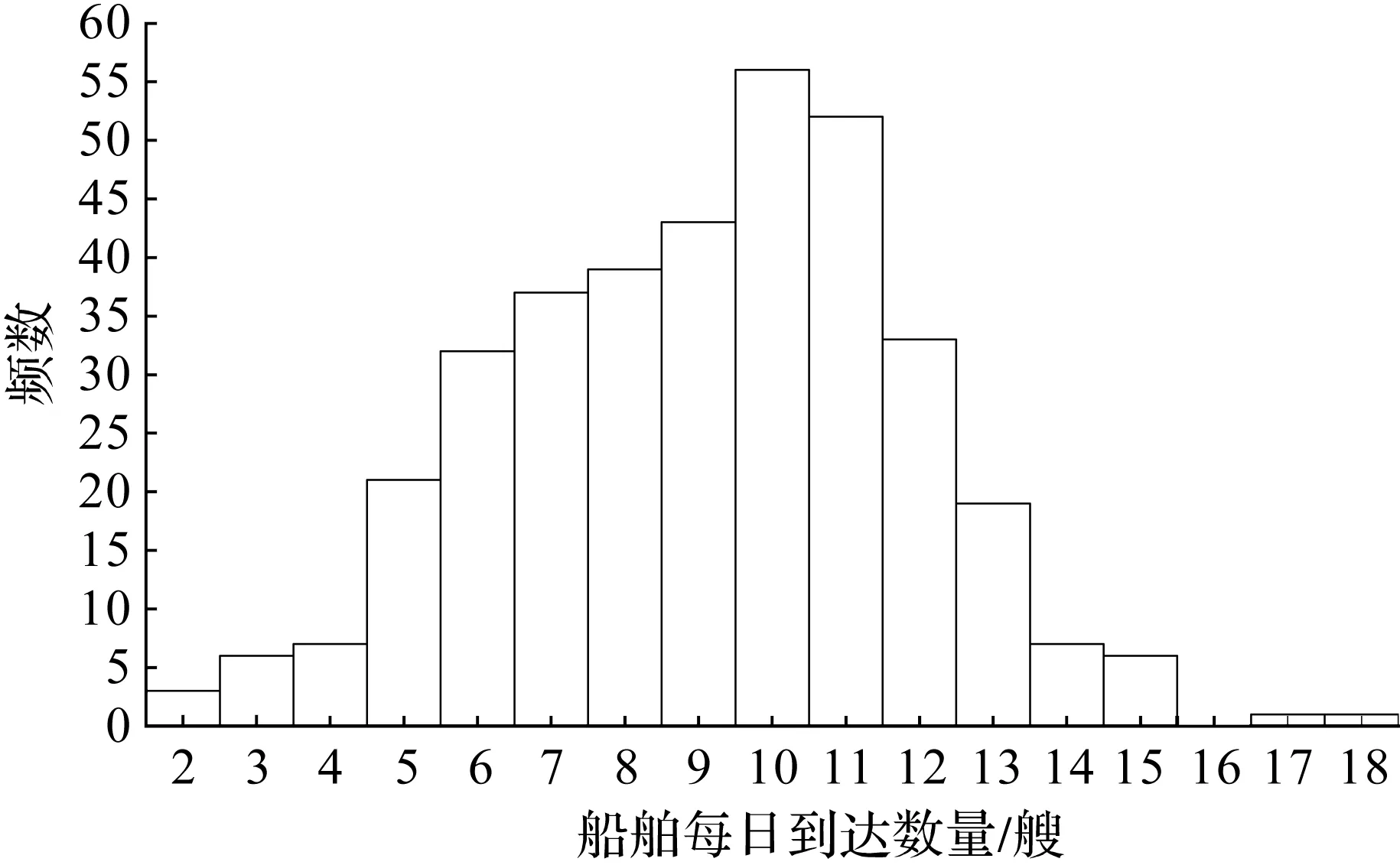
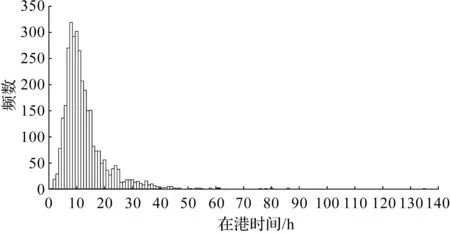





3.2 数值分析






4 结 论
