自适应遗传算法支持下的既有铁路曲线整正方法

2023-02-02明祖涛李颖喆赖祖龙

测绘工程 2023年1期

明祖涛，李颖喆,2，李玮，赖祖龙

(1.中国地质大学(武汉) 地理与信息工程学院，武汉 430074；2.武汉市勘察设计有限公司，武汉 430022)

在铁路工程中，当施工放样误差造成工程结构物偏移或后期运营过程中线路逐渐发生变形错位时，特别是铁路曲线路段，为避免损失，需调整线路的技术参数以恢复平顺性。此类铁路曲线整正问题中，为减少工作量，一般以拨距总量最小作为优化的方向。目前铁路曲线整正方法主要有绳正法、偏角法和坐标法3种。绳正法和偏角法都是根据渐伸线理论，容易产生较大误差，坐标法计算原理严密清晰、精度高，越来越被广泛地应用到实际生产中[1-14]。

国内外专家学者们利用多种数学优化技术提高了传统拨距计算的精度和效率。例如，文献[1]提出按最小二乘原理的整体平差方法，结合测点坐标的曲率图对主要桩点进行稳健估计，通过两次平差获得优化结果。文献[2]使用霍夫变换剔除线性识别中的偏差点，使曲率图更加准确，进而提高最小二乘法计算精度。文献[3]考虑运行稳定性与舒适度，以通过定点作为约束条件，用网格法计算可行性解的组合范围。文献[4-6]通过拟合三次样条曲线来逼近铁路曲线，结合曲率变化特征进行概略分段，用概略桩点作为初始方案进行迭代计算求拨距量最优值。文献[7]提出坐标法计算径向拨距新方法，并采用网格法验证该方法的精确性。文献[8-10]用多种最优化方法进行了实验，分析约束优化和无约束优化的可行性，与网格法进行比较。拟合与最优化方法在铁路曲线整正问题上能够满足工程精度要求，但需要先通过识别曲率变化特征来确定主要桩点，而曲率图具有一定误差，且该过程难以加入约束条件与计算精确里程。文献[11-14]利用粒子群算法或遗传算法生成初始方案群，简化线型识别过程，能够顾及经济、环境指标与相关规范等限制条件。

在分析常用的铁路整正方法的基础上，提出一种利用自适应遗传算法的优化整正方法，其优势在于适应度函数的变量在个体的并行计算中作为已知值，能够叠加黄金分割法搜索主要桩点，并计算其在对应拨后曲线的精确里程。通过大量实验数据验证，该方法能够获得曲线要素全局最优解，具有较高的精确性和适用性。

1 坐标法拨距计算

1.1 坐标转换

以直缓点为原点，直缓点到交点方向为x轴正方向、曲线偏移方向为y轴正方向建立平面直角坐标系，各曲线要素如图1所示。

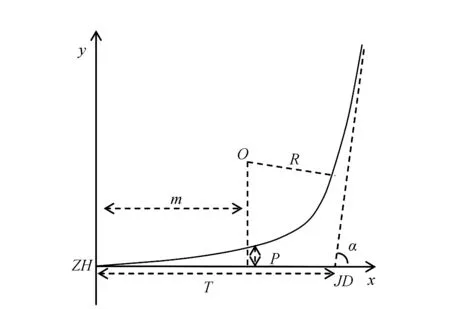
图1 曲线要素示意图

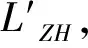
(1)

(2)

(3)

(4)

(5)

式中：T0为原设计切线长；T为拨后曲线的切线长；α为转向角，由前后夹直线确定，在优化中不发生改变；l0为缓和曲线全长；R为圆曲线半径；m为切线增量；P为圆曲线内移值；ZH为线路直缓点；JD为线路转弯处两条直线延长线交点。

1.2 拨距计算

曲线拨正后，除ZH点改变外，曲线线型变化也使测点的对应位置改变，各测点里程应重新计算。

d=|Yi|.

(6)

缓和曲线坐标公式参考文献[15]，一般保留前三项级数。l为曲线长，由曲线上各点里程减直缓点里到，R为圆曲线半径。

(7)

(8)

式中：xi，yi为位于曲线上且与测点i里程对应的坐标。

(9)

式中：圆心坐标(Xa，Ya)=(m，R+P)。

圆曲线坐标公式为：

(10)

(11)

4)当测点对应第二缓和曲线时，以缓直点为原点建立缓直点切线直角坐标系，可按文献[16]中讨论的方法进行坐标转化，拨距量计算与第一缓和曲线相同。

5)由于拨距量为测点沿径向到拨后曲线的距离，缓和曲线曲率半径为Rl0/l，曲线各微分弧段的半径为R到无穷大，远大于以测点为圆心与曲线的切圆，则拨距量为关于里程的单峰凸函数，可使用黄金分割算法[17]求解拨距量和测点里程。当R和l0作为已知值时，令拨距量与里程的函数关系为d=f(x)，算法流程如图2所示。

图2 黄金分割法求解拨距流程

图2中：a，b为测点里程搜索范围；x1，x2为黄金分割法的三等分点。

1.3 变量范围与约束条件

缓和曲线长、圆曲线半径上下界根据原设计值设置，并满足《铁路线路设计规范 TB10098-2017》《普速铁路线路修理规则TG/GW102-2019》等规范，其中缓和曲线总长度应为10 m的整倍数，特殊困难地段整进至1 m，拨距最大限值30 mm。此外，约束条件还有为避免重要构筑物改建而引入的控制点。

2 自适应遗传算法

遗传算法是一种基于遗传进化原理的随机化搜索最优值方法，通过模拟物竞天择的自然法则，优秀个体的染色体有更高的概率保留并通过选择、变异、交叉的遗传学原理使种群中的下一代不断进化。整个种群的适应度逐步提高，在朝预期方向进化过程中诞生最优个体。在解决拨距优化问题中使用保留最优个体和自适应交叉变异算子的改进策略，可克服种群早熟，以提高全局搜索能力。

2.1 选择算子

保留父辈中最佳个体存放在子代个体矩阵第一行，其他子代个体采用比例选择法加入矩阵，第i个个体被选中的概率为：

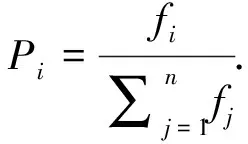
(12)

2.2 自适应的交叉、变异算子

种群保持多样性是遗传算法有效运行的前提条件，需要保持足够多的不同个体和较高的变异概率，同时为了加快收敛速度，必须使种群尽快向最优方向靠拢，但又会降低种群的多样性，自适应遗传算法大多致力于解决此矛盾。其中自适应的交叉、变异算子作为一种简便易行的方法，以最大适应值与平均适应值的差值作为判断染色体早熟程度的标准。当差值较大时，种群保持了较好的多样性，增大交叉概率Pc、减小变异概率Pm，以加快收敛速度；差值较小时，Pc减小Pm增大，有利于克服早熟现象[18]，可按式(13)、式(14)设置[19]。

(13)

(14)

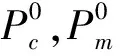
2.3 适应值函数与优化步骤

基于自适应遗传算法的坐标法拨距优化计算流程如下：

1)输入外业测量坐标，进行坐标转换。根据R、l0原设计值和规范要求设置上下界，在变量阈值范围内等间隔生成一定的个体，进行种群初始化；

2)个体的曲线要素R和l0作为已知值，用其对新线路分段，再利用黄金分割法求取各测点拨距量与对应里程，最后累加拨距量;

3)计算个体的适应度，保留适应度最高的个体，其他子代个体采用比例选择法选择父代；

4)繁衍过程中使用自适应交叉、变异算子；

5)当目标函数最小值持续20代不再变化时停止进化，否则回到步骤(2)；

6)输出优化结果。

3 实验分析

3.1 仿真实验

仿真实验数据通过已知的曲线要素，等里程间隔生成多组无误差的坐标作为拨距优化的原始数据，曲线优化前后对比见表1。在大量仿真实验中，文中方法优化得到的缓和曲线长度l0与圆曲线半径R和设计值相比其差值几乎为零，计算精度优于0.1 mm，由此可见，文中采用的方法具有较高的计算精度。

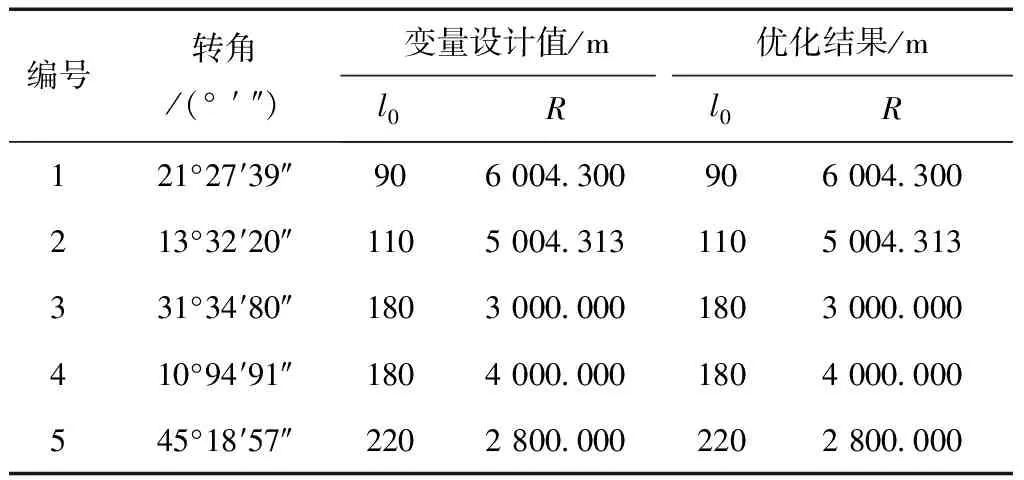
表1 自适应遗传算法优化仿真实验结果

3.2 应用实例

选取文献[10]中R为1 000 m，l0为40 m的曲线坐标作为工程实例1。实例2的数据来源于某铁路隧道进口，通过测量二次衬砌的超量，内业计算得到里程间隔为5 m的一组铁路左线坐标。选用文献[20]中R为665 m，l0为50 m的数据作为实例3，文献[21]中R为600 m，l0为50 m的数据作为实例4。

自适应遗传算法参数设置为：种群规模200，扩大个体数量有利于克服过早收敛，但会增加计算时长。交叉概率为0.8，变异概率0.05，超过连续不进化代数20时停止。自适应遗传算法优化实例一得到各测点拨后里程和拨距量，列出部分测点结果如表2所示。

表2 实例一测点拨距量统计

由表2可知，黄金分割法求得的拨后里程与直接使用式(1)计算得到的里程有明显差别。通过1号点的里程计算的遗传算法优化后的切线长，比原设计切线小0.123 7 m，但测点12的里程比原里程大0.375 7 m，相差约0.252 m，同样计算其他实例中里程最大的测点，相差分别为0.005 m、0.014 m、0.000 1 m，初始里程越粗略该差值越大，通过黄金分割法求取精确拨后里程能够排除该误差，从而提高优化精度。

在拨距优化的最优化方法中，无需二阶导信息的拟牛顿法显示出收敛快、精度高的特点[9]。使用Matlab优化工具箱中提供的拟牛顿法，用曲线要素原设计值进行初始化，迭代求得变量l0，选择l0附近的两个10的整倍数值作为已知值，再次计算得到目标函数最小值与变量R。

采用网格法、最优化方法、自适应遗传算法3种方法对该4组实例中的曲线进行优化，变量设置相同的上下界，其中网格法设置缓和曲线步长10 m，圆曲线半径步长0.1 m，统计4次结果如表3所示。