考虑地层三维空间分布的盾构掘进模拟

张超 ，徐智文 ，刘飞香 ，陈仁朋 †，周苏华 ，廖金军 ，胡伟飞

（1.湖南大学 土木工程学院，湖南 长沙 410082；2.建筑安全与节能教育部重点实验室（湖南大学），湖南 长沙 410082；3.中国铁建重工集团股份有限公司，湖南 长沙 410100；4.浙江大学 机械工程学院，浙江 杭州 310027）

盾构法是城市地下空间开发的主要施工方法，被广泛应用于城市地下交通隧道建设.盾构掘进本质上是盾构机与地层动态耦合作用的过程.地质环境复杂多变导致盾构机服役性态难预测，是盾构掘进施工风险的主要诱因，极易引起地表坍塌、开挖面失稳、盾构机姿态偏移和刀盘结泥饼等工程事故.因此，有必要开展盾构掘进模拟以获取施工过程中装备受力状态和地层扰动规律［1-5］.然而，现有盾构掘进模拟通常将地质环境简化为平行成层地层［6-9］，难以反映盾构服役地质环境的三维空间变异性.

复杂地质环境的定量表征一般通过三维地质建模实现.三维地质建模可提供地层信息的几何模型，需要借助额外的算法进一步生成有限元网格.然而，地质模型的三维空间变异性给相关算法研究带来挑战.目前，一些学者利用地质构造面、地层界面、软弱夹层等特殊界面对地质模型进行分块处理，并对独立封闭块体进行网格划分，成功构建了复杂地层数值模型［10-13］.此类地层数值模型主要应用于边坡稳定性分析、洞室稳定性分析等岩土工程问题［14-16］.目前，尚无三维地质建模技术在盾构掘进模拟中应用的相关报道.

本文提出了一种考虑地层三维空间分布的盾构掘进模拟方法.首先利用Kriging 算法基于钻孔数据建立三维地质模型，提出一种基于地层分界面的条件判断算法，克服了传统方法中复杂地层曲面带来的有限元网格畸变等问题，实现三维复杂地层的高质量网格划分；然后，编写了相应的复杂地层盾构掘进模拟前处理程序，实现复杂地层盾构掘进模拟的参数化建模，大幅提高建模效率；最后，以长沙地铁四号线某区间为例，讨论了所提方法的适用性.

1 三维地质建模

三维地质模型可定量表征复杂地层的地质信息，为构建复杂地层有限元模型提供几何模型.三维地质建模包括地表及地层分界面的高程插值计算和模型可视化两部分.

1.1 Kriging算法

在地质统计学理论中，Kriging 算法是对区域化随机变量进行无偏最优估计的空间插值算法.该算法在矿产空间分布以及地质模型构建方面具有广泛应用.下面以高程插值为例，介绍该算法的主要插值过程：将待插值点X0的高程定义为Z*（X0），且已知n个钻孔样本的数据，并将第i个钻孔与地表或地层分界面的交点Xi的高程定义为Z（Xi），则Z*（X0）可表示为n个Z（Xi）的加权求和［17］，见式（1）.

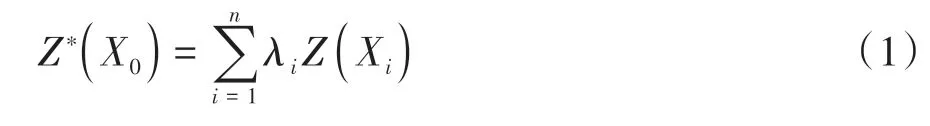
式中：λi（i=1，2，…，n）为权重系数.Kriging 插值过程即为通过理论变异函数γ（h）构建的Kriging 方程组［18］求解最优权系数的过程，方程组见式（2）.

式中：γ（hij）是由交点Xi、Xj的水平间距hij确定的理论变异函数值；γ（hi0）是由交点Xi和插值点X0的水平间距hi0确定的理论变异函数值；μ是拉格朗日乘子.此处，理论变异函数是两点水平间距与高程变异性的函数，可通过拟合实验变异函数值获取，见图1.实验变异函数值则由钻孔样本数据计算得到.球状变异函数和实验变异函数值分别见式（3）和式（4）.

图1 球状变异函数模型Fig.1 Spherical variogram model

式中：γ（h）为理论变异函数；C0为块金常数；C为拱高；a为变程；h为样本点间水平间距.

式中：γ*（h）为实验变异函数；N（h）表示水平间距为h的钻孔样本对数量；Xi与Xi+h分别表示上述钻孔样本对与地表或地层分界面的交点.

如此，Kriging 算法首先由钻孔样本数据得到离散的实验变异函数值，并利用球状模型等数学模型拟合离散值得到理论变异函数，再将理论变异函数代入Kriging 方程组解得插值点的最优权重系数λi，最后根据公式（1）得到该点的高程.

1.2 建模流程

三维地质建模流程具体包括：钻孔样本预处理、变异函数求解、地表及地层分界面高程计算、三维地质模型可视化共四个步骤.

1.2.1 钻孔样本预处理

钻孔样本预处理的目的是保证所有钻孔的地层类别和层序一致，以便采用统一数据格式对钻孔样本的地层信息进行存储和调用.根据所有钻孔样本提供的地层信息，对每个钻孔揭露的地层按照沉积顺序进行编号，见图2.当钻孔样本缺失某地层时，在地层缺失处插入厚度为零的该地层，从而保证所有钻孔的地层类别和层序相同.

图2 钻孔样本预处理Fig.2 Borehole sample pretreatment

1.2.2 变异函数求解

基于预处理后的钻孔样本，采用公式（4）计算地表、各地层分界面的实验变异函数γ*（h），并利用公式（3）对离散的实验变异函数值进行拟合，得到理论变异函数γ（h）.

1.2.3 地表及地层分界面高程计算

对地表或地层分界面进行离散，并以离散的待插值点的水平投影作为网格节点，形成图3 所示虚拟背景网格.以点X0高程插值为例，根据点X0、Xi和Xj的投影位置得到hi0和hij，代入理论变异函数γ（h）计算得γ（hi0）和γ（hij），再代入Kriging 方程组求解得到权重系数λi，求解出X0高程.按上述过程可得到地表及地层分界面上所待插值点的高程数据.

图3 地层分界面的虚拟背景网格Fig.3 Virtual background grid of stratum interface

1.2.4 三维地质模型可视化

将地表及地层分界面上插值点的平面坐标和高程数据导入自主搭建的可视化平台，得到三维地质模型，如图4所示.

图4 三维地质模型示意图Fig.4 3D geological model diagram

2 复杂地层网格划分

由于复杂地层的强空间变异性，构建的三维地质模型通常具有不规则的几何形态，难以直接生成高质量有限元网格.因此，有必要针对复杂地层开发高效有限元网格划分算法.

复杂地层盾构掘进模拟的有限元网格划分难点主要体现在两个方面.一方面，直接基于地质模型的网格划分方法在地层尖灭处易导致网格畸变，不利于数值计算收敛，见图5（a）；另一方面，当盾构隧道穿越图5（b）所示的复杂地层时，隧道边界与地层分界面相交并形成若干不规则几何边界，这些不规则几何边界易形成畸形网格.

图5 复杂地层盾构掘进模拟网格划分难点Fig.5 Difficulties in grid division of complex strata

针对上述两方面问题，本文提出一种基于地层分界面的条件判断算法.该方法从三维地质模型提取模型几何边界和地表及地层分界面高程数据，前者直接输入网格划分算法生成未赋予材料属性的地层网格，后者输入条件判断算法以甄别地层网格单元的地层类别并赋予其材料属性，最终建立复杂地层的有限元模型.

基于地层分界面的条件判断算法流程见图6.具体流程如下：

图6 复杂地层网格划分流程图Fig.6 Flow chart of complex formation grid division

1）基于Gmsh编写地层网格生成脚本，实现地层网格的自动化划分.该脚本采用六面体单元对地质模型几何边界确定的建模区域进行均匀网格划分，生成初始地层网格，且该网格模型与三维地质模型采用相同坐标系.在初始地层网格中，盾构掘进区域设置为网格协调区，见图7，得到未赋予材料属性的地层网格.

图7 网格协调区示意图Fig.7 Diagram of grid coordination region

2）读取上述地层网格数据，计算单元i（i=1，2，…，n；n为单元总数）的中心点坐标（Xi，Yi，Zi）.

3）读取三维地质模型高程数据，搜索各地层界面上与单元i中心点水平投影重合的点，并将该点的高程命名为Zlj（j为地层界面序号；j=1，2，…，N；N为地层界面总数），其中Zlj＞Zlj+1，见图8.

图8 条件判断示意图Fig.8 Diagram of conditional judgment

4）对比各地层界面高程值Zlj与单元i中心点高程值Zi，进而确定单元i的地层类别.由地表（Zlj，j=1）开始，判断Zlj≤Zi是否成立，若成立则判断单元i位于第j-1 层地层，继续第5 步；否则令j=j+1，再次判断，直到满足Zlj≤Zi.

5）重复步骤2）～4），对地层网格模型中所有单元进行逐一判断，形成各地层的网格单元集.

6）对各地层单元集赋予相应的土体物理力学参数，完成复杂地层的有限元模型构建.

通过上述步骤可得到图9 所示的复杂地层有限元模型，该模型包含了三维地质模型的地质信息.

图9 融合三维地质信息的复杂地层有限元模型Fig.9 Finite element model of complex strata incorporating 3D geological information

3 复杂地层盾构掘进模拟前处理程序

为实现盾构掘进快速参数化建模，基于上述方法采用C#语言编写了复杂地层盾构掘进模拟前处理程序.该程序包括3 个模块：复杂地层有限元建模模块、盾构隧道掘进建模模块和计算求解模块，见图10.复杂地层有限元建模模块具备三维地质建模功能和地层有限元建模功能，可利用钻孔数据文件快速建立融合三维地质信息的地层有限元模型.在盾构隧道掘进建模模块设置隧道几何与掘进参数后，可自动生成盾构掘进模型的inp文件.计算求解模块通过批处理命令调用通用有限元求解器ABAQUS，并读取盾构掘进模型的inp文件进行计算，最终实现复杂地层条件下盾构掘进数值模拟.

图10 复杂地层盾构掘进模拟前处理程序Fig.10 Pre-processing program for simulation of shield tunneling in complex strata

在复杂地层盾构掘进模拟前处理程序输入隧道几何和掘进参数，即可实现盾构掘进的快速参数化建模.隧道几何设置涵盖隧道埋深、隧道直径、管片尺寸等参数.隧道掘进参数设置包括掘进步长、掌子面支护系数、管片和土体材料等参数.

基于上述输入参数，盾构隧道掘进建模模块可自动完成以下四方面设置，并生成inp文件：

1）分段开挖设置.在每个掘进步中，采用“生死”单元法移除掌子面前方土体单元，同时激活盾构管片单元，实现分段开挖过程的模拟.

2）掌子面支护力设置.将掌子面的静止土压力作为支护力默认值，沿高度方向呈梯度分布.每个掘进步可根据实际施工资料设置掌子面支护系数，将该系数乘以默认支护力得到实际支护力.

3）地层损失设置.盾构掘进引起的地层损失是导致地表沉降的主要因素，常以地层损失率［19］表示，并可通过整环扰动层近似模拟［20］.通常盾体与围岩间的间隙具备不均匀性，即拱顶间隙大于两旁和底部间隙［21］.为近似考虑该不均匀性，本文将扰动层分为上下两半环分别设置材料参数，见图11.上半环扰动层参数取上部围岩参数折减值；下半环扰动层采用邻近围岩的材料参数.

图11 地层损失设置示意图Fig.11 Diagram of stratum loss setting

4）材料设置.复杂地层盾构掘进模拟前处理程序包括线弹性本构模型和摩尔库伦本构模型，前者用于管片和上半环扰动层，后者用于土体和下半环扰动层.

4 工程案例验证

本节以长沙地铁四号线区间隧道施工工程为例，利用前处理程序构建盾构地层掘进模型，并开展掘进模拟.将沿隧道轴线的地表沉降模拟结果与实测数据对比，探讨本文所提方法的有效性.

4.1 工程概况

长沙地铁四号线桐梓坡—望月湖区间隧道全长1 512 m，该区间段采用土压平衡盾构机掘进施工，盾构机外径为6.28 m.该区段为双线隧道.本文选取先期施工的左线隧道掘进引起的地表沉降数据进行验证分析.隧道位置与钻孔平面分布见图12.依据钻孔样本数据，利用所编写的前处理程序构建该区域的三维地质模型，见图13.

图12 隧道与钻孔分布平面图Fig.12 Plan view of tunnels and borehole distribution

图13 三维地质模型Fig.13 3D geological model

图14 为沿隧道纵轴线方向的地质剖面图.该区段内地层复杂多变，自上而下分别为素填土、硬塑黏土、强风化板岩、中风化板岩和微风化板岩.各地层的物理力学参数见表1.

表1 地层物理力学参数表Tab.1 Physical and mechanical parameters of soils

图14 地质剖面图Fig.14 Longitudinal geological profile

4.2 盾构掘进模拟与验证

为研究地层空间变异性对地表沉降的影响，采用表2 所示盾构隧道几何和掘进参数，将其输入复杂地层盾构掘进模拟前处理程序建立图15 所示盾构掘进有限元模型，并开展盾构掘进模拟.

表2 盾构隧道几何和掘进参数表Tab.2 Geometry and excavation parameter of shield tunnel

图15 盾构掘进模拟有限元模型Fig.15 Shield tunneling simulation finite element model

为验证有限元模型的准确性，选取掘进断面内极软岩占比为50%与100%的两种工况，分别对应711 环和730 环地表沉降监测点，并对比两种工况下地表沉降变化过程的模拟结果与实测结果，见图16.根据盾构施工工法，盾构掘进对监控断面地表沉降的影响分为两个阶段，盾构掘进抵达监控断面前称为第一阶段，盾构通过监控断面后称为第二阶段.在地表沉降规律方面，两种工况下，两阶段的模拟结果与实测结果趋势均一致.在第一阶段期间，地表沉降均随掌子面与监控断面的距离减小而逐渐增大，而在第二阶段期间，地表沉降增长变缓且最终趋于稳定.在沉降幅值方面，两种工况下地表产生了超过10 mm 的差异沉降量，具体为：当盾构机由掘进断面部分极软岩地层进入全断面极软岩地层时，地表最终沉降量模拟与实测分别增加了11.67 mm 和18.02 mm，模拟与实测的误差为35%.误差主要来源于730环，根据施工资料，盾构机开挖至730环停机约10 h，而有限元模型无法考虑停机时未及时注浆引起的地层损失，因此730 环最终沉降模拟值小于实测值.综上，有限元模拟结果与实测结果趋势一致，吻合程度好，表明有限元模型计算准确.

图16 监测点地表沉降变化过程模拟与实测结果对比Fig.16 Comparison of simulation and measured results of surface subsidence change process at monitoring points

为研究地层空间变异性对地表沉降的影响，将各监测点最终沉降的模拟结果和实测数据绘制于图17 中.模拟结果显示，地表最终沉降随掘进断面内极软岩占比增大而显著增加，与实测数据规律一致.综合图16～17 结果，掌子面接近监测断面前，开挖卸载作用引起掌子面前方极软岩地层发生变形，导致地表发生第一阶段沉降.掌子面通过监测断面后，极软岩地层向隧道断面内发生位移，导致第二阶段地表沉降.当极软岩占比增加时，上述两阶段的地表沉降均增大，进而导致地表最终沉降显著增加.

图17 沿隧道轴线地表最终沉降模拟与实测结果对比图Fig.17 Comparison of simulation and measured results of final settlement along tunnel axis

综上，复杂地层盾构掘进模拟前处理程序可实现盾构掘进快速参数化建模，所建有限元模型能较准确地反映复杂地层条件下盾构掘进过程，并能有效揭示地层空间变异性对地表沉降的影响规律.

5 结 论

本文提出了考虑地层三维空间分布的盾构掘进模拟方法，编写了相应的复杂地层盾构掘进模拟前处理程序，并以长沙地铁四号线区间隧道工程为例，验证了所提方法和相应程序的有效性.主要结论如下：

1）基于地层分界面的条件判断算法可以规避复杂地层曲面的有限元网格畸变问题，并且有效解决了复杂地层曲面与隧道断面的网格协调问题.

2）复杂地层盾构掘进模拟前处理程序集成了三维地质建模功能和复杂地层网格划分算法，实现了复杂地层掘进模拟的参数化建模，大幅提高了建模效率.

3）盾构掘进模拟结果表明，地表沉降量随盾构掘进断面内软岩占比增大而显著增加，与工程实测数据规律一致，验证了本文所提方法的有效性.