竖向荷载作用下悬索桥纵向变位特征与机理

黄国平 ，胡建华 ，万田保 ，华旭刚 ，封周权 ，陈政清

（1.湖南大学 土木工程学院，湖南 长沙 410082；2.湖南城市学院 土木工程学院，湖南 益阳 413000；3.湖南省交通水利建设集团有限公司，湖南 长沙 410008；4.中铁大桥勘测设计院集团有限公司，湖北 武汉 430050）

悬索桥因其强大的跨越能力不断应用于跨越大峡谷、跨海及联岛工程中，然而大跨悬索桥具有的轻柔、低阻尼及非线性等结构特点，在荷载作用下变形大、振动问题突出.其竖向变形及振动得到了较多的关注，而纵向变形问题往往被忽视，然而实际工程中，悬索桥加劲梁梁端一般设置纵向滑动支座，允许加劲梁纵向运动，以避免设置固定支座而导致的巨大纵向支座反力和增大结构设计难度［1］.因此，运营及环境荷载作用下，悬索桥加劲梁梁端将产生较为明显的位移.梁端位移是悬索桥设计计算时的重要参数，一方面，该位移是梁端附属装置诸如伸缩缝、支座及阻尼器的设计与选型的重要设计参数；另一方面，近年来研究表明：悬索桥梁端的纵向位移运动特性与其梁端附属装置诸如伸缩缝装置、滑动支座及梁端阻尼器的耐久性及使用寿命密切相关［2-5］，并且在服役环境下加劲梁频繁的纵向运动与主缆位移不同步，亦可能导致短吊杆过早失效［6-8］.

很多学者对悬索桥纵向位移行为进行了相关研究，目前研究评估悬索桥纵向位移是通过桥梁健康监测数据和有限元数值分析两个主要途径来实现的.Ni 等［9］基于梁端纵向位移长期监测数据对梁端伸缩缝工作状态进行了评估，建立了平均温度与梁端纵向位移相关性模型，该项研究主要关注平均位移特性，没有对梁端瞬态位移进行研究；Guo 等［10］以两座悬索桥和一座斜拉桥梁端纵向位移监测数据为对象，对比分析两种桥型梁端纵向位移特征，指出在车辆作用下悬索桥桥型更容易发生纵向位移，并形成巨大的累计位移行程.类似的研究还有文献［11］和文献［12］等.

李光玲等［13-14］基于有限元方法建立了考虑伸缩缝刚度的悬索桥计算模型，分析了车流作用下的悬索桥梁端纵向累计位移；赵越等［15-16］以实测车流数据为荷载激励输入悬索桥有限元模型，计算分析了主梁梁端纵向位移峰值及梁端累计位移响应；韩大章等［17］建立了有限元模型，研究了悬索桥在随机车辆荷载下梁端纵向位移响应；万田保等［1］探讨了悬索桥纵向位移特征，并定性地阐述了该纵向位移产生的机制，但并没有给出纵向位移理论支撑和计算方法.此外，有不少学者研究了中央扣对悬索桥纵向变形及振动行为的影响，如王连华等［18］通过有限元仿真分析研究了车辆作用下中央扣对加劲梁梁端纵向位移的影响；胡腾飞等［19］则采用动力测试并结合有限元分析的方法研究了中央扣对大跨悬索桥模态特性的影响.类似的研究还有文献［20-22］等，但中央扣的纵向约束机制仍欠清晰.

上述研究不管是基于监测数据还是有限元数值计算，均研究了复杂工况下的悬索桥静、动态梁端纵向位移，但很少涉及悬索桥纵向变形或纵向振动产生机制.为此，本文基于缆索变形理论建立悬索桥主缆及加劲梁纵向变位分析的理论方法，揭示竖向荷载作用下悬索桥主梁纵向位移产生机理，给出一种纵向位移计算的新的实用算法，并研究中央扣的抑制机理并研究了中央扣的纵向约束机制.

1 竖向荷载下的主缆变形特征分析

1.1 主缆变形特征

主缆不仅是悬索桥结构的第一受力体，且其力学特性决定了整个悬索桥的结构行为.为此，以主缆为对象，剖析其竖向荷载下的变形特征，并进行变形位移分析.若不考虑塔顶水平位移，则主缆可简化为单跨缆索结构，其竖向荷载作用下的计算简图如图1所示.

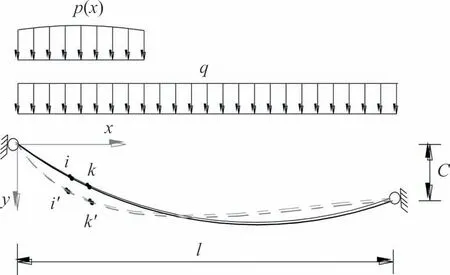
图1 单跨缆索结构计算简图Fig.1 Single-span cable structure calculation diagram

在恒载q（q为常量）作用下的初始线形方程如式（1）所示［23］：

相应的缆索张力水平分力为：

若此时继续作用竖向活载p（x），则索初始线形发生改变，变形后的线形可为终态的线形，此时相应地索张力水平分力由Hq变到Hp+Hq.

取图1 中长为ds的微段索单元ik为考察对象，其变位关系如图2 所示，根据其几何变位关系，并忽略高次微量后可得［24］：

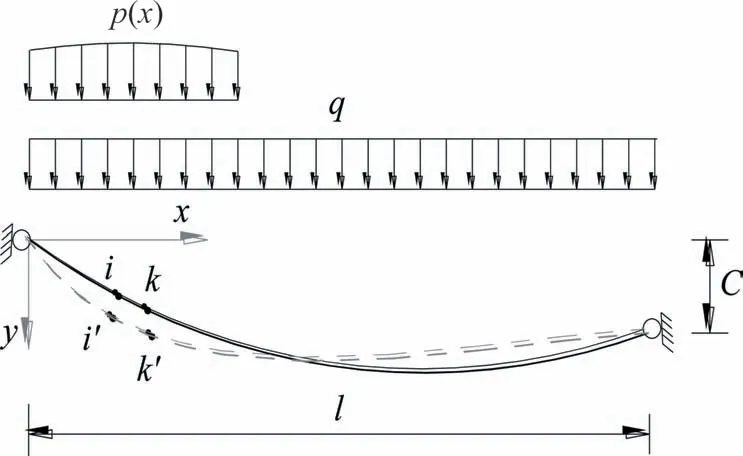
图2 缆索微段变位示意图Fig.2 Diagram of cable micro-segment displacement

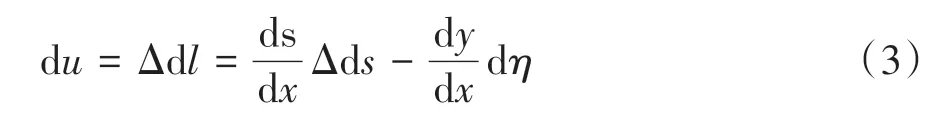
式中：du、Δds分别为微元索单元的伸长量水平投影（跨径方向的伸长量）和切线伸长量；η为竖向活载引起的缆索竖向挠度增量.

暂不考虑温度变化，则索伸长量仅由索张力导致，有：

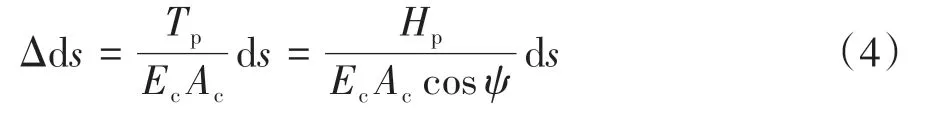
式中：Tp、Hp分别为活载引起的缆索张力及其水平分量；EcAc、ψ分别为缆索的轴向刚度和倾角.

将式（4）代入式（3）可得：

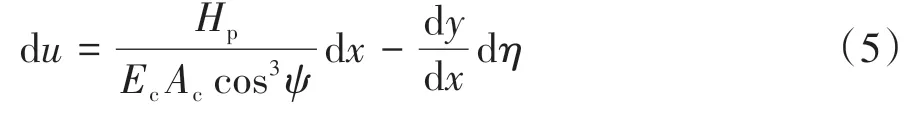
对式（3）进行从索端点到任意位置x的变上限积分，便可得到缆索任意位置的纵向位移：

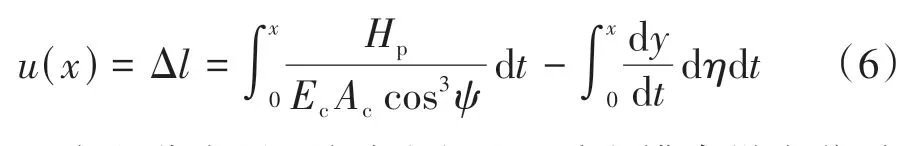
式中：t为积分变量.从式（6）可以看出缆索纵向位移由两部分构成，第一项是由索张力引起的弹性变形位移，第二项为竖向挠度增量η引起的纵向偏移，一般可不考虑索张力的弹性变形的伸长［25］，则有：

若悬索桥塔顶等高，则式（1）中C=0，并将其代入式（7），则有：

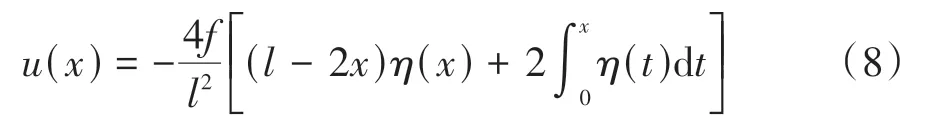
式（7）或（8）实际上反映了主缆竖向位移和纵向位移的耦合关系，在竖向荷载作用下主缆主要以改变初始几何线形的方式来抵抗外荷载作用，体现了缆索大位移柔性索的力学特征，决定了在竖向荷载作用下将可能导致悬索桥纵向变形的特性.

1.2 主缆变形位移分析

1.2.1 主缆竖向位移

采用缆索线形与简支梁弯矩图比拟的方法对主缆线形求解［25-26］，柔性索受任意分布荷载q（x）作用，若不考虑缆索受弯刚度，有竖向平衡方程：

而根据材料力学理论，梁受任意竖向分布荷载q（x）作用时，其平衡方程为：

观察对比式（9）和（10），二者形式完全相同，y与M相互对应，且索与梁边界条件一致时，下列关系成立：

式（11）表明，索与梁边界条件相当时，y与M可相互比拟，根据简支梁弯矩即可确定缆索线形的曲线形状，补充一个约束方程求解出H，便可完全确定缆索终态线形.

现以承受竖向均布荷载p为例，基于能量原理并结合弯矩比拟法来求解竖向活载作用下的缆索线形或挠度增量η.与悬索等跨径简支梁分别在q、p作用下的弯矩图如图 3所示.

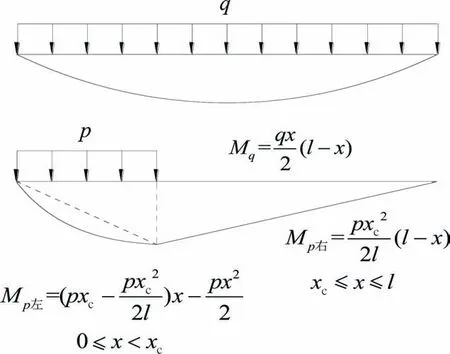
图3 恒载、活载下简支梁弯矩图Fig.3 Bending moments diagram of a simply supported beam under dead load and live load

简支梁在恒载q作用下的弯矩为：

简支梁在均布活载p作用下的弯矩为：

式中：xc为竖向均布荷载p的加载长度.

将式（12）代入式（11），将式（12）加上式（13）代入式（11）可分别得初态和终态缆索线形：

式（15）减去式（14），可得均布荷载p作用下缆索的缆索竖向挠度增量η：

缆索由初态过渡到终态过程中，考虑整个外力（q及p）对体系做功之和可表示为：

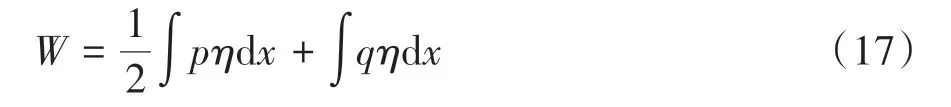
考虑到实际工程中使用荷载远小于初态恒载，可认为η与p近似呈线性关系，根据能量守恒原理，外力做功之和等于内力做功之和，内力做功转化为结构体系的应变能，如前所述，工程中的使用荷载量级下，可不考虑缆索的伸长［25］，即外荷载只改变了缆索线形，外力做功仅转为体系的重力势能，因此有：

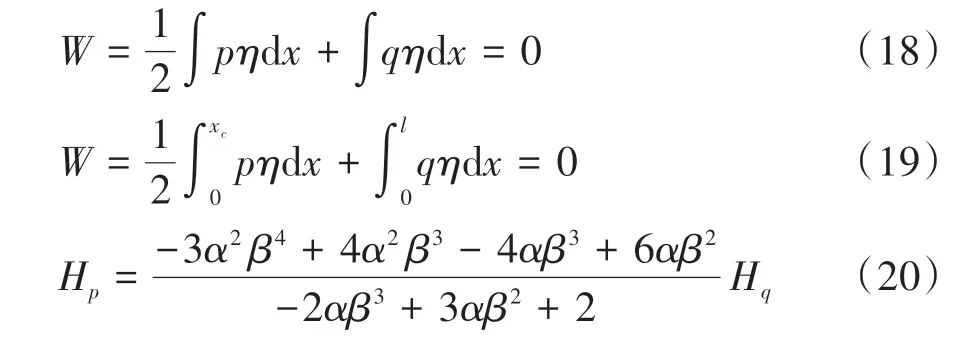
式中：无量纲参数β=xc/l，竖向均布荷载与恒载比α=p/q，恒载荷载作用下缆索水平拉力按式（2）计算得到.

同理，可求得集中荷载作用下的挠度增量η：

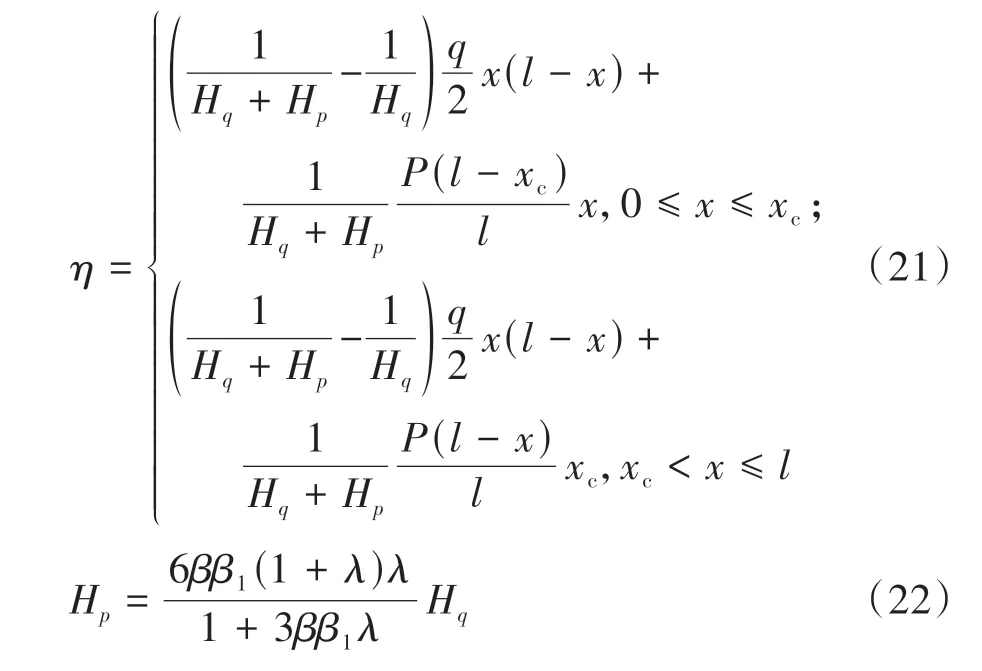
式中：xc为竖向集中荷载P作用点位置坐标；β=xc/l、β1=1-β为无量纲参数；λ=P/ql为竖向集中荷载与恒载比；恒载荷载作用下缆索水平拉力按式（2）计算得到.

1.2.2 主缆纵向位移

将式（14）代入式（8），即可得竖向均布荷载下的主缆纵向位移：

将式（21）代入式（8），可得竖向集中荷载下的主缆纵向位移为：作用下的若干典型变形示意图.实际上，竖向荷载作用下悬索桥变形特征是由前述1.1 节主缆变形特性所决定的，由于竖向荷载导致主缆发生纵向偏移，由此引起竖吊杆倾斜，加劲梁在倾斜吊杆水平分力作用下纵向位移而达到新的平衡位置（见图5、图6）.加劲梁纵向位移具有反对称属性特征，对称荷载下并不会引起加劲梁的纵向位移运动，只有非对称或反对称竖向作用下才能导致主梁的纵向位移，因此加劲梁纵向位移是由不平衡竖向荷载所导致.由结构力学可知，任何形式荷载的作用，均可以分解为对称荷载和非对称荷载，如图5（a）和图6（a）加载模式可分别分解为图5（b）（c）和图6（b）（c）.

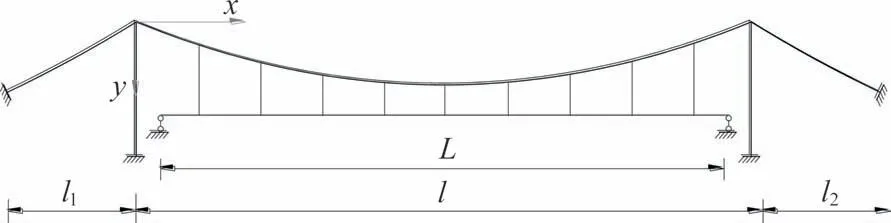
图4 单跨悬索桥结构示意图Fig.4 Structure diagram of the single-span suspension bridge

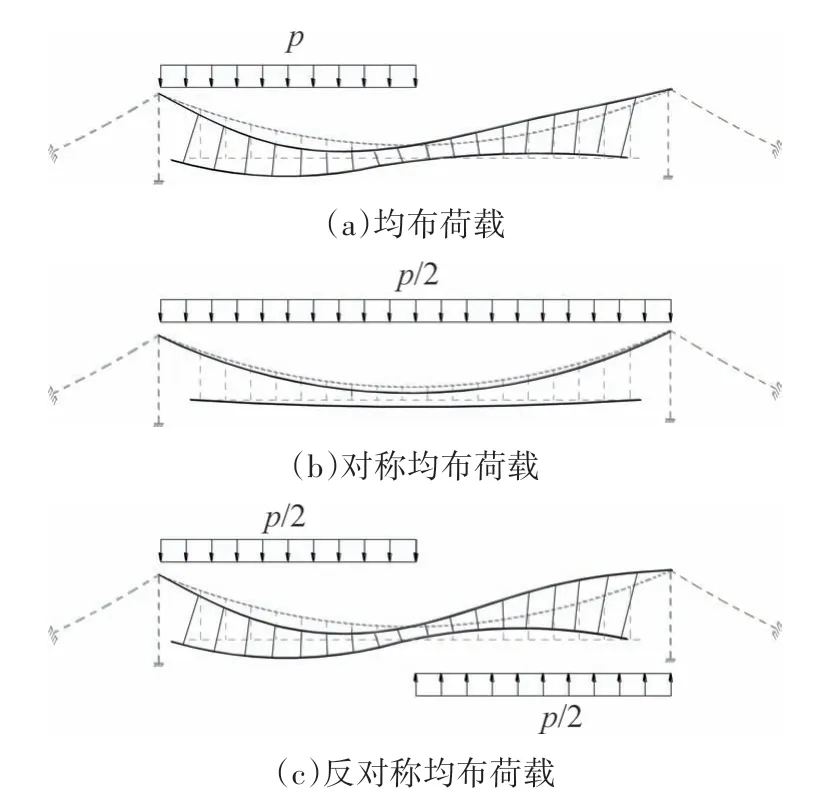
图5 均布荷载作用下悬索桥变形Fig.5 Deflection of the suspension bridge under uniform load

2 竖向荷载下的悬索桥纵向变位

图4 为一典型单跨简支悬索桥示意图，在一般情况下加劲梁梁端设置纵向滑动支座，允许加劲梁纵向位移，以降低荷载作用时的内力效应和支座设计难度.在竖向荷载（汽车活载）作用下，悬索桥不仅发生竖向挠曲变形，而且可能会产生纵向偏移位移，由此导致加劲梁及梁端较大的纵向位移.

2.1 悬索桥变形特征

图5、图 6分别为悬索桥在均布荷载和集中荷载

需要说明的是：由于考虑了缆索的几何非线性，叠加原理已不适用，图5（a）和图6（a）中荷载作用下的变形位移与图5（b）（c）和图6（b）（c）中相应荷载作用下的位移之和并不精确相等，但这不影响定性地分析竖向荷载引起的悬索桥变形特征.

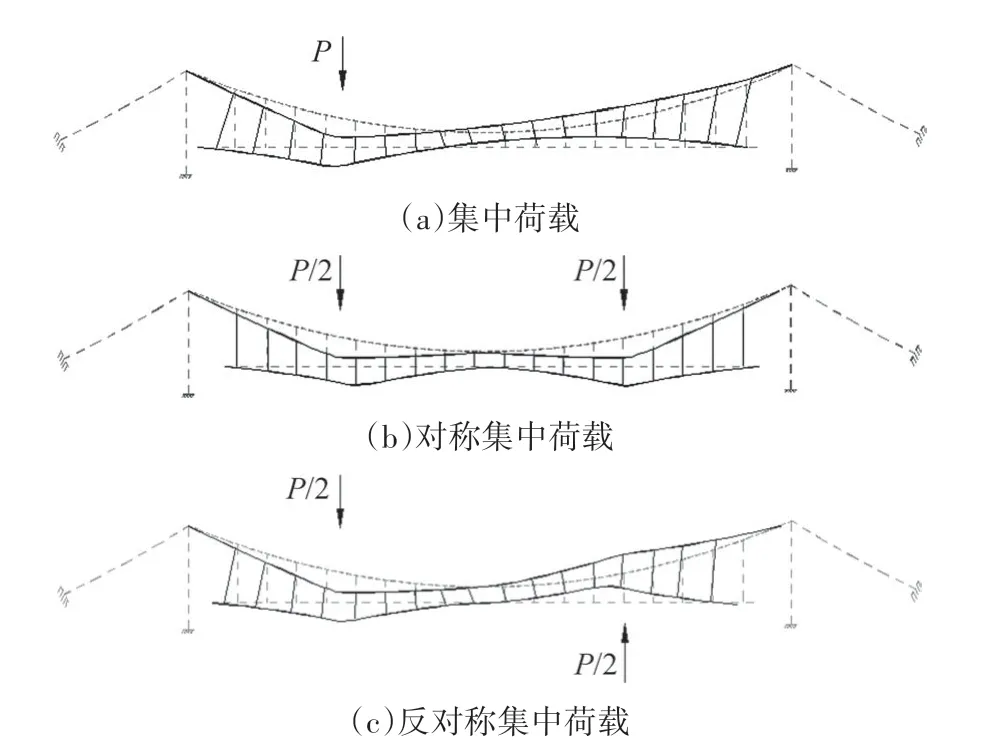
图6 集中载作用下悬索桥变形Fig.6 Deflection of the suspension bridge under concentrated load

2.2 加劲梁纵向位移

对于仅设置竖吊杆的传统悬索桥，变形后吊杆发生倾斜，当倾斜吊杆水平分力合力为零时，加劲梁达到终态平衡位置，根据此平衡条件，可以得出加劲梁的纵向位移.

取第i根吊索处的主缆及加劲梁微段为对象，并忽略加劲梁挠曲变形导致的纵向位移，其位移情况如图7所示.

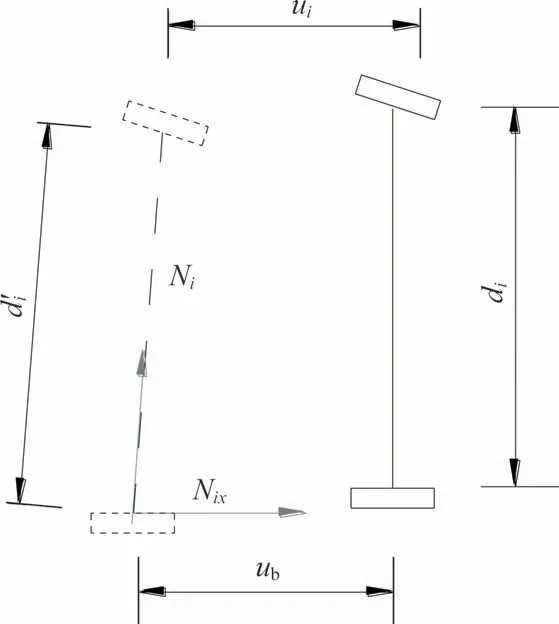
图7 第i根吊索处主缆及加劲梁微段位移Fig.7 Displacements of the main cable and stiffening girder at the ith slice

有如下关系：

式中：Ni、Nix分别为第i根吊杆力及水平分力；ui为第i根吊杆处主缆纵向位移；ub为加劲梁纵向位移；di、di′分别为变形前后的吊杆长度.

若忽略吊杆伸长（即di=di′）以及竖向荷载导致的吊杆增量，并假设每根吊杆的拉力均为N，则有：

由加劲梁纵向平衡条件可得：

将式（26）代入式（27）可得：

若考虑加劲梁竖向挠曲引起的梁端转角，则可得到梁端的纵向位移：

式中：h上、h下分别为加劲梁中和轴的顶、底高.

式（28）反映出加劲梁纵向位移与主缆纵向位移之间的关系，对于只设置竖吊杆的悬索桥，竖向荷载导致的加劲梁纵向位移（刚体位移）为主缆纵向位移对吊杆长度倒数的加权平均，对于该式的求解关键在于ui或u（x）的确定.

对悬索桥而言，一般可假设成桥恒载均由主缆承担，而活载由加劲梁与主缆共同承担，因此此时主缆的纵向位移u（x）求解困难，但当满足一定假设条件时，悬索桥主缆位移仍可按1.2节单索结构的计算方法求解：

1）假设塔顶不发生纵向位移；2）对于大跨度悬索桥而言，其主缆的重力刚度远大于加劲梁的抗弯刚度［28］，可忽略加劲梁刚度贡献；3）有限采用“挠度理论”的假设，不考虑吊杆伸长，加劲梁与主缆同竖向挠度η，计算η时不考虑纵向位移；4）不考虑倾斜吊杆水平力对主缆的反作用影响.

2.3 中央扣约束机理

在悬索桥跨中设置中央扣是大跨度悬索桥常见的一种构造措施，用以改善悬索桥受力状态，约束加劲梁的纵向运动.为明确中央扣对加劲梁的纵向约束机制，从中央扣受力平衡及变形协调出发，分析非对称竖向荷载作用下中央扣对加劲梁纵向运动的约束影响，并推导相应的加劲梁纵向位移计算公式.

在非对称竖向荷载作用下，跨中处主缆与加劲梁变形如图8 所示，可以看出有无中央扣变形的本质差别.无中央扣的悬吊体系可视作瞬变“摆锤体”（图8（a））；而斜拉中央扣的存在使得跨中附近的主缆、加劲梁、斜拉中央扣及竖吊杆成为一个整体，可视作“刚片”区，“刚片”区在跨中发生整体转动，此时吊杆与主缆及加劲梁基本垂直（见图8（b））.

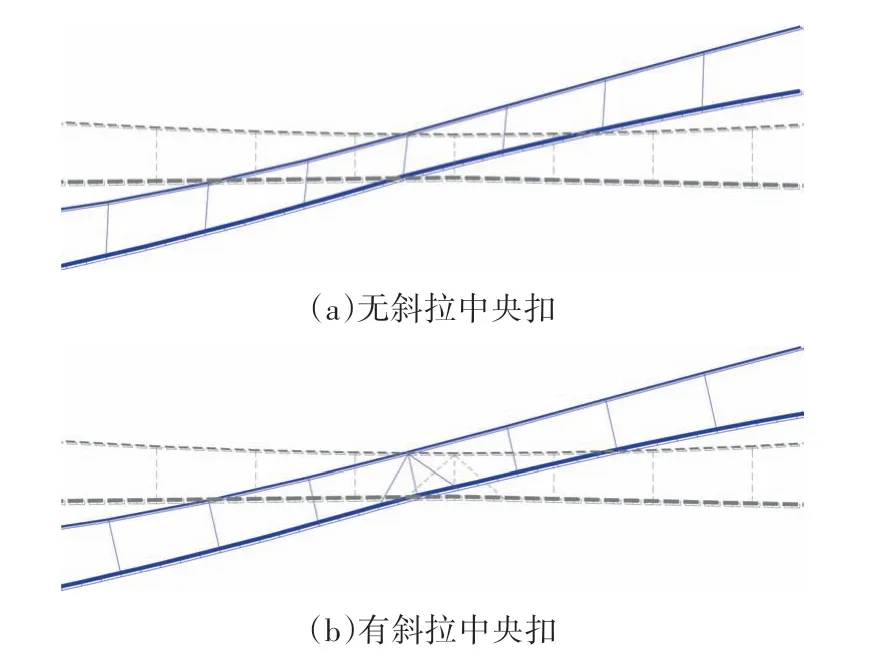
图8 跨中主缆与加劲梁变形示意图Fig.8 Deformation diagram of the mid-span main cable and stiffening girder

图9 所示为跨中中央扣与加劲梁变位移关系，中央扣随加劲梁整体发生转角φ，并产生侧向弹性位移Δ，跨中主缆纵向位移满足如下变形协调关系式：

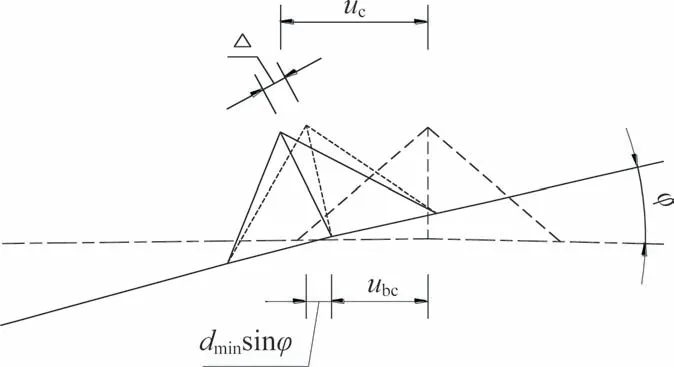
图9 跨中中央扣与加劲梁变位关系Fig.9 Relationship between the mid-span central buckle and stiffening girder displacement

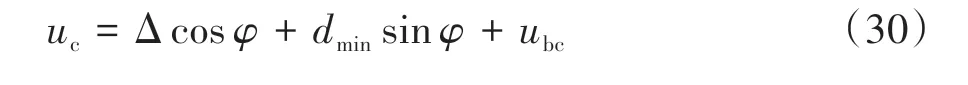
式中：dmin为跨中短吊杆的长度；ubc为跨中加劲梁与短吊杆交点的纵向位移，其与加劲梁纵向平均位移的关系为：

常规荷载水平作用下，φ为极小值，整理式（30）可得：

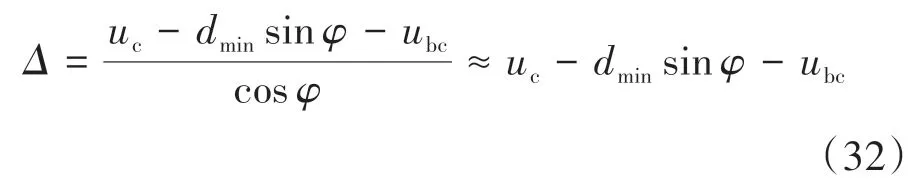
去除主缆对加劲梁纵向约束，以加劲梁、竖吊杆及中央扣为对象，则根据纵向平衡条件，原式（27）改写为：

并有主缆对中央扣的水平约束力

式中：kc为柔性中央扣侧向刚度.

竖吊杆倾斜后水平分力

式中：ks，i为单根吊杆的侧向刚度.

将式（32）代入式（34），再将式（35）及式（34）代入式（33）可得：

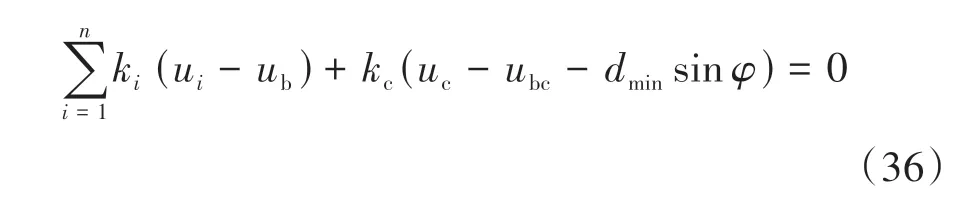
将式（31）代入（36），可得：

式中：d′=dmin+h上.

若不考虑中央扣对主缆变形的影响，吊杆处主缆纵向位移ui，可仍按式（8）计算求得，对于均布荷载和集中荷载工况仍分别按式（23）、式（24）获得.

对于柔性中央扣单元的侧向刚度，按力学分析计算可得［29］：式中：Ecb、Acb分别为斜拉扣弹性模量和截面积；a为

单根吊杆的侧向联结刚度可根据图 7 或式（26）获得：

对于无中央扣的情况，即式（38）中kc=0，则式（38）蜕化为式（28）；当设置n对柔性中央扣时，可近似将kc乘以n作为多对中央扣的刚度代入式（38）；当采用刚性中央扣时，kc=∞，式（38）改写为：

3 算例分析

3.1 工程概况与计算模型

长江上某单跨悬索桥整体立面布置图如图10所示.大桥主缆与加劲梁跨度均为838 m，矢跨比为1/10，两个边主缆水平长度分别为250 m 和215 m.加劲梁采用钢-混凝土组合截面，加劲梁全宽33.2 m，高2.8 m.全桥设52 对竖吊杆，沿桥纵向水平间距为16 m，端部吊杆水平间距为19 m；主塔采用混凝土结构，塔高为107 m.桥梁恒载集度约343 kN/m，该悬索桥有限元模型如图 11所示.

图10 桥跨布置立面图（单位：m）Fig.10 Elevation of the suspension bridge（unit：m）

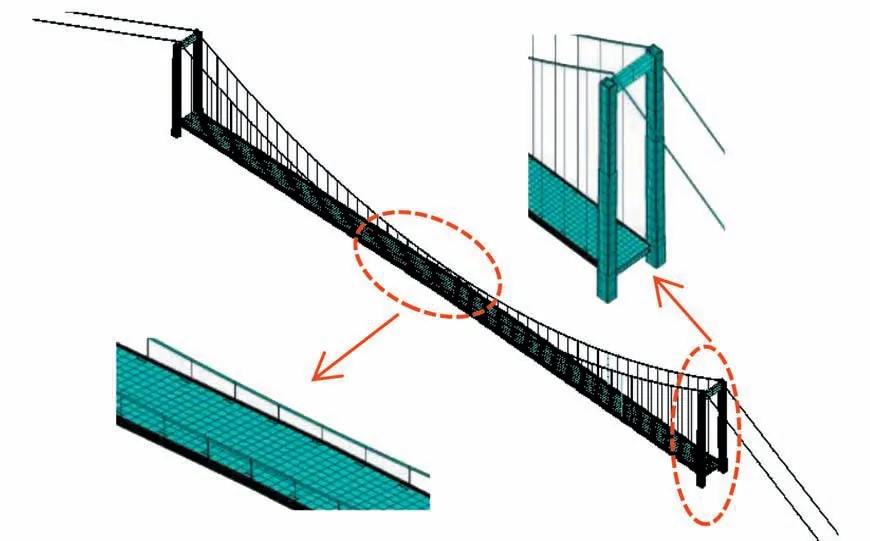
图11 悬索桥有限元模型Fig.11 Finite element model of the suspension bridge

3.2 计算结果对比分析

针对均布荷载及集中荷载两种典型竖向荷载工况，进行有限元计算分析并与理论解法对比，将部分有代表性的计算结果列于图12～图16 和表1、表2中，可得如下结论：

1）有限元数值计算与理论计算结果较为接近（见图12～图16和表1、表2），对于集中荷载及均布荷载作用下，两种计算方法得到的加劲梁纵向位移的最大误差分别为5.7%和5.4%（见表2）.

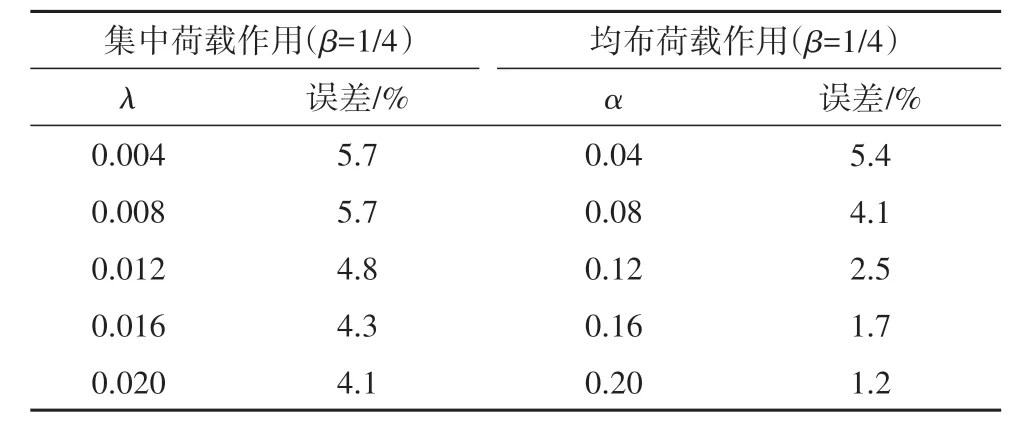
表2 加劲梁纵向位移误差Tab.2 Error of girder longitudinal displacement

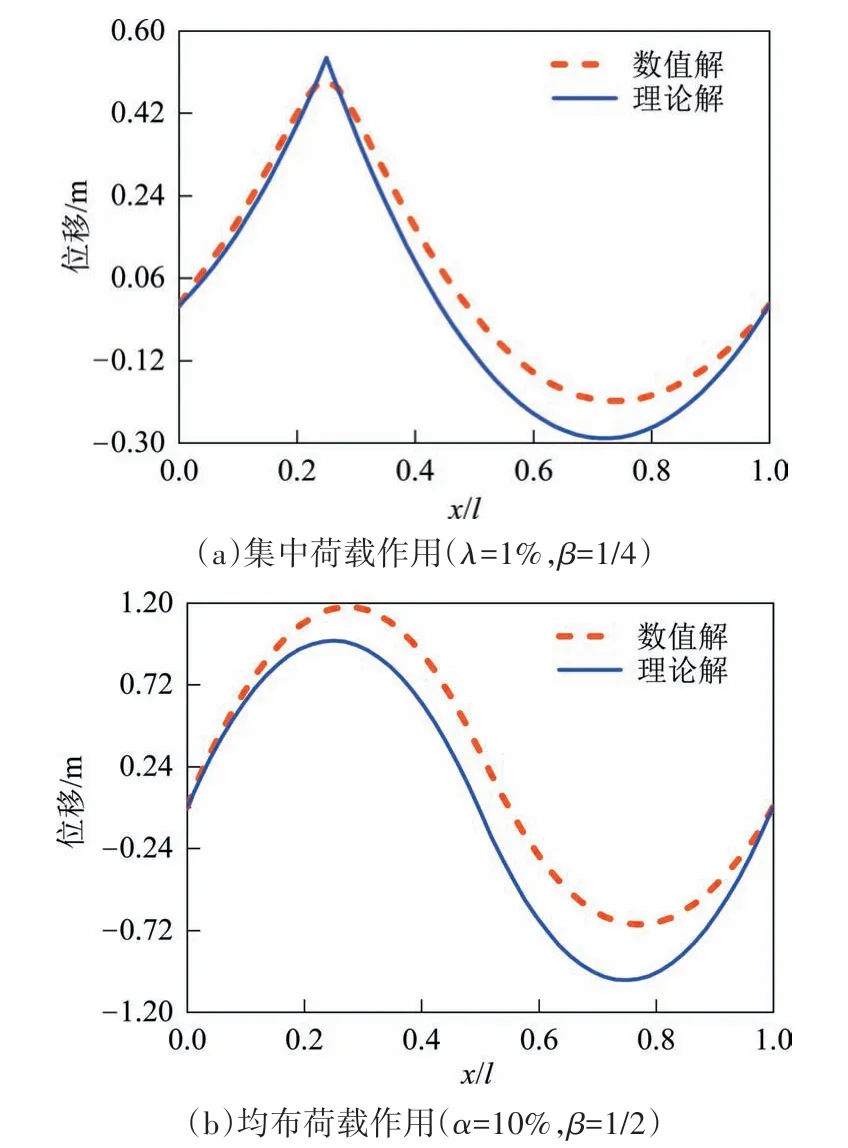
图12 竖向荷载作用下主缆竖向位移曲线Fig.12 Vertical displacement curve of the main cable under vertical loads

2）图13 为主缆及加劲梁的纵向位移曲线，反映出在竖向荷载作用下，主缆纵向位移变化起伏较大，而加劲梁变化较小，主要表现为刚体纵移，在使用荷载作用下吊杆容易弯折；加劲梁纵向位移平均值与梁端位移见表1，二者差异甚小，表1 所示的计算工况中为理论计算结果大于数值计算结果，其最大误差分别为4.4%和2.7%，加劲梁挠曲弹性变形导致的梁端纵向位移可以忽略.

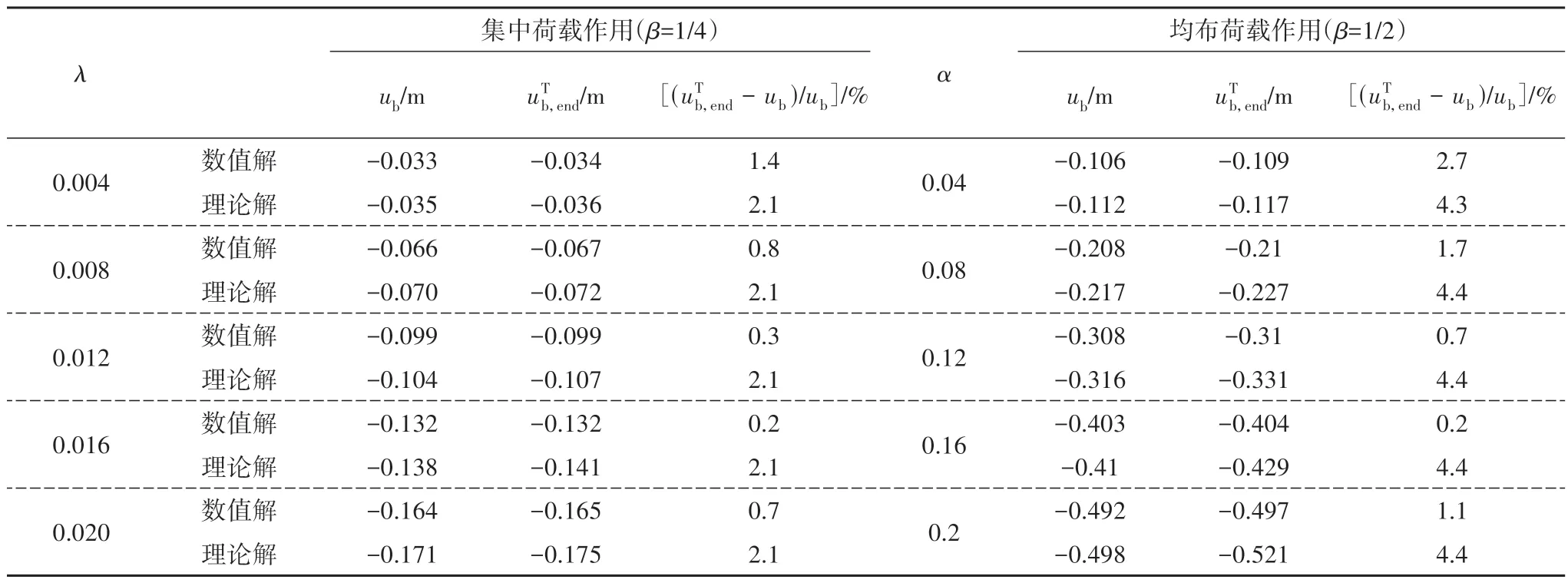
表1 加劲梁纵向位移平均值与梁端纵向位移对比Tab.1 The average longitudinal displacement value of the girder and the longitudinal displacement at the girder end

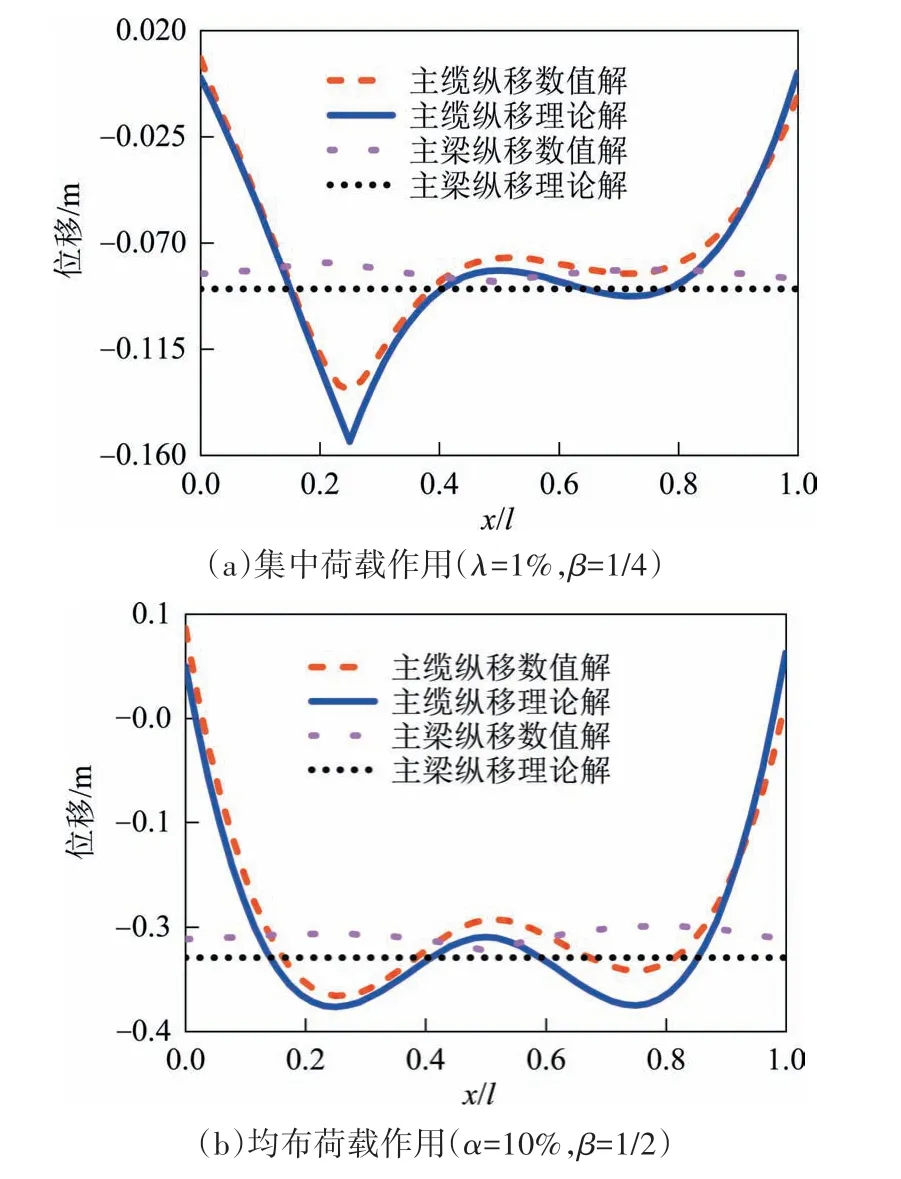
图13 竖向荷载作用下主缆及加劲梁纵向位移曲线（无中央扣）Fig.13 Longitudinal displacement curve of the main cable and stiffened girder

3）加劲梁纵向位移随竖向荷载增大而增大，当荷载较小时，二者为线性关系（见图14（a）），而荷载水平相对较高时，呈弱非线性（见图14（b））.

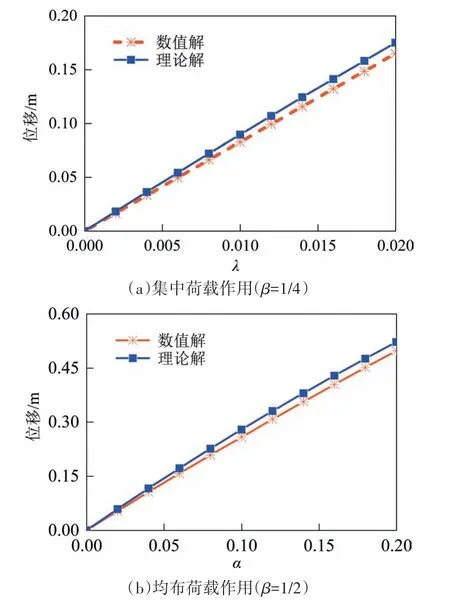
图14 荷载-加劲梁纵向曲线（无中央扣）Fig.14 Longitudinal curve of the load-stiffening girder

4）加劲纵向梁位移随集中荷载位置变化而变化，变化趋势形如正弦曲线，四分之一跨位置为最不利加载位置，图15（a）所示本质为车致悬索桥主梁拟静态纵向位移，且当集中荷载P=1 时，所得位移曲线即为加劲梁纵向位移理论影响线；加劲纵向梁位移随均布荷载的加载长度增大而先增大后减小，半跨加载最为不利，加载长度与主梁纵向位移曲线在跨中位置对称（见图 15（a）），体现了非对称荷载导致加劲梁纵向位移的变位特征.

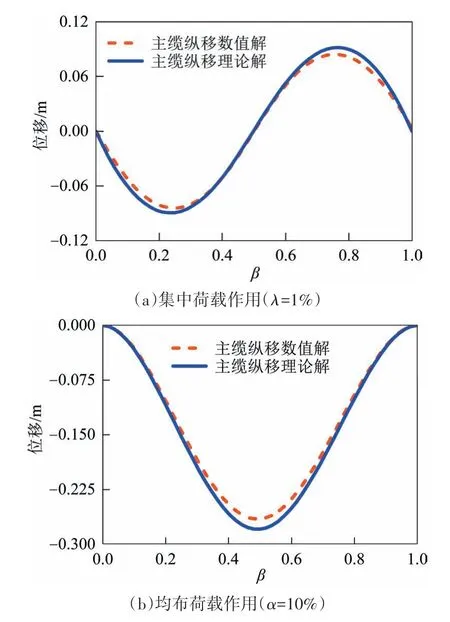
图15 β-ub相关曲线Fig.15 β-ub correlation curve

3.3 中央扣影响分析

建立跨中设有一对柔性中央扣、三对柔性中央扣及刚性中央扣等多种悬索桥有限元模型.模型中采用LiNk10 单元模拟柔性中央扣，其轴向刚度取480 MN；对于刚性中央扣，采用文献［20］中的构造形式（BEAM44梁单元模拟）.计算结果列于图16～图19（因篇幅所限，图16～图18 仅示出集中荷载（λ=1%，β=1/4）工况，从上述计算结果可得如下结论：

1）中央扣的设置对悬索桥挠度和主缆纵向位移的影响可忽略不计（见图16、图17），2.3.2 节中假设成立，可见中央扣并不能提高悬索桥竖向刚度.

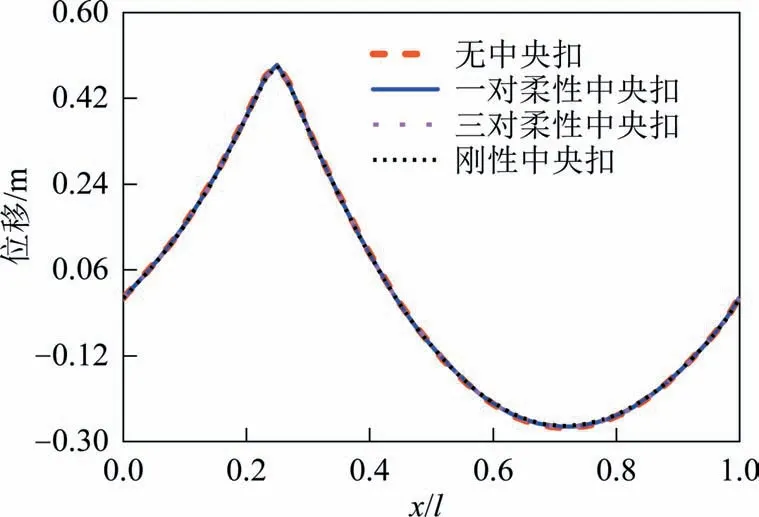
图16 集中荷载作用下主缆竖向位移曲线（不同中央扣）Fig.16 Vertical displacement curve of the cable under concentrated load

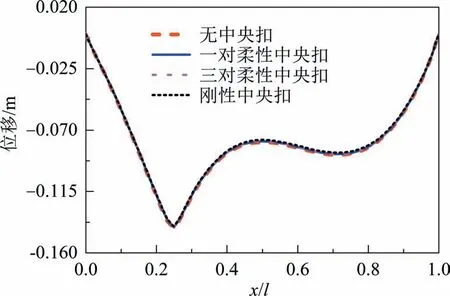
图17 集中荷载作用下主缆纵向位移曲线（不同中央扣）Fig.17 Longitudinal displacement curve of the cable under concentrated load

2）对于集中荷载作用（λ=1%，β=1/4）、均布荷载作用（α=10%，β=1/2），虽两种荷载作用工况模式及荷载量级均差异较大，但图19 所示的加劲梁纵向位移-中央扣刚度相关曲线趋势相似.加劲梁的纵向位移随中央扣刚度的增大而减小，但约束效率不断降低，文中算例中采用三对柔性中央扣时，约束效果与刚性中央扣效果接近（见图18、图19）.

图18 集中荷载作用下加劲梁纵向位移曲线Fig.18 Longitudinal displacement curve of the stiffened girder under concentrated load

3）有限元数值计算得到不同中央扣刚度下的加劲梁纵向位移（见图19 中散点），与理论结果吻合较好，说明式（38）可靠.该式及图19 所示关系曲线可指导设计者进行中央扣设计与参数分析.

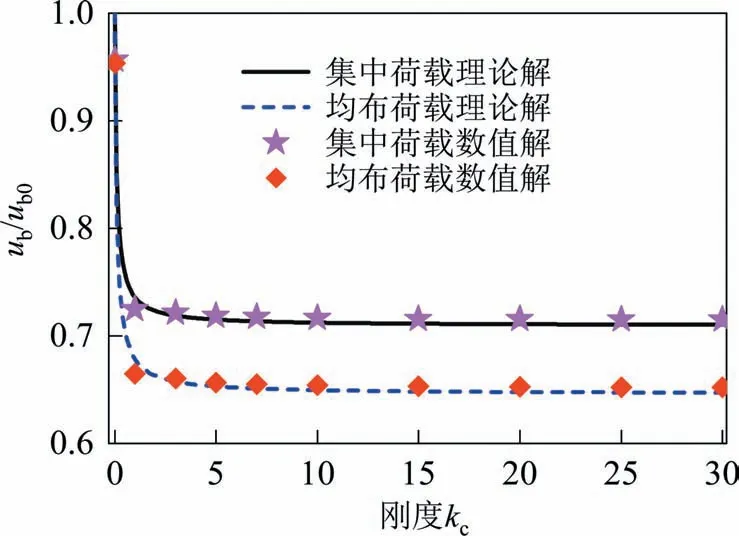
图19 加劲梁纵向位移与中央扣刚度相关性曲线Fig.19 Correlation curve between the girder longitudinal displacement and the stiffness of the central buckle

4 结论

1）基于单索结构变形理论，由缆索变位协调条件，可得缆索变位特征，即竖向位移与纵向位移相互耦合相关，竖向位移可以引起纵向位移；在荷载作用下，缆索主要依靠改变其几何形态来抵御外荷载，即外力做功转为体系势能，这是柔性索几何非线性的本质体现.

2）对于悬索桥而言，非对称竖向荷载作用下，主缆发生纵向偏移，加劲梁因吊杆及中央扣等的侧向联结作用而发生纵向位移.

3）对于传统悬索桥，其纵向如瞬态“摆锤体”，在非对称竖向荷载下，在吊杆倾斜水平分力作用下纵移至终态平衡位置；而对于跨中设有中央扣的悬索桥，跨中处中央扣、竖吊杆、主缆及加劲梁会形成一个“刚片”区，在非对称竖向荷载下，“刚片”区作为一个整体而发生转动位移，该转动位移可减小加劲梁的纵向位移，即中央扣抑制纵向位移的机理.

4）本文所提纵向位移计算公式与数值解进行比较，二者计算结果吻合好，所得方法可指导设计者在初步设计时进行梁端纵向位移估算和参数分析；所得主梁纵向位移-中央扣刚度曲线表明，加劲梁的纵向位移随中央扣刚度的增大而减小，但约束效果不断降低，文中算例结果表明，当采用三对柔性中央扣时，其纵向约束效果接近刚性中央扣.

5）本文研究对象为单跨悬索桥，对静态竖向荷载作用下悬索桥纵向变形行为进行了深入研究，但所提主梁纵向位移计算方法对多跨悬索桥和多塔悬索桥的适用性，以及车辆荷载作用下的悬索桥纵向行为还有待进一步研究；此外，基于有限元数值结果，结合现场实测，并运用统计学方法进行分析，还有待进一步开展.