高压水射流喷水推进装置空化流动及推力特性仿真分析
2023-01-31暴春航龙新平梁蕴致张祖提张增磊
暴春航,龙新平,梁蕴致,张祖提,张增磊
(1.水射流理论与新技术湖北省重点实验室,湖北 武汉 430072;2.武汉大学 动力与机械学院,湖北 武汉 430072;3.武汉第二船舶设计研究所,湖北 武汉 430072)
引言
随着全球陆地资源日益匮乏,世界各国纷纷将战略目标转移到海洋,海洋资源的开发和利用将直接关乎国家未来的发展命运。水下航行器是海洋资源开发的重要装备,推进装置是决定航行器性能的关键,各国都在积极推动对水下航行器及其推进方法的研究[1]。传统的水下航行器主要采用螺旋桨推进,而螺旋桨在高速旋转工作时极易产生空化现象,引起巨大的流体噪声并加剧系统振动,螺旋桨的工作效率由于空化现象的影响而受到了严重的制约[2-3]。高压水射流喷水推进技术是一种新型的水射流推进技术,区别于以轴流泵/混流泵为动力部件的传统叶轮式喷水推进装置,其主要利用高速水射流而形成反推力。由于高压水射流喷水推进器取消了叶片式结构,避免了旋转叶轮易受空化影响而降低效率的现象,提高了系统抗空化能力,同时其还具有系统结构简单、扬程高、体积小、推重比大、易实现矢量推进等优点,开始被应用于水下航行器推进[4-9]。
近年来,学者们针对高压水射流喷水推进装置的快速性能、机动性能、隐蔽性能进行了研究。喷嘴是高压水射流喷水推进装置的关键部件之一,是影响推进装置反推力和快速性能的重要部件,YANG等[10]构建了考虑能量损失和喷嘴参数的水射流反推力模型,并优化了喷嘴设计,SHI等[11]通过实验和CFD模拟研究了不同的喷嘴尺寸、喷嘴形状对推进装置反推力的影响,得出了相比于锥形和指数型喷嘴,流线型喷嘴得到的反推力更大的结论。LIANG等[12]分析了不同喷嘴的几何参数和动态参数对反推力的影响,并为自主水下航行器喷水推进系统中的喷嘴设计提供了指导原则。为提高推进装置的机动性能,ZHANG等[7]提出了一种高压水射流喷水推进装置与推力矢量控制系统相结合的方案,极大地提高水下航行器的机动性以及可操作性。李秋坪[13]对推进装置的噪声特性进行了数值模拟,为降低噪声辐射,提高水下航行器的隐身性能提供了理论指导。
当高压流体流经喷嘴后,会形成高速射流,当局部压力降至工作温度下的饱和蒸气压以下时,将产生空化[14-16]。空化的产生将破坏液体的宏观连续性,单相液体流将转化为气液两相流。因此,流场的特征和工作介质的物理属性会因空化的产生而变化,进而导致反推力也受到影响[17]。LIANG等[12]在改变喷嘴几何参数对反推力的影响时,初步考虑了气液两相流的影响。ZHANG等[18]在结合数值模拟与试验验证推导反推力理论时,利用Realizablek-ε模型与ZGB空化模型相结合,探究了空化现象对系统反推力的影响,并建立了基于动量方程和空化理论的推力数学模型。而高压水射流喷水推进装置产生的高速水射流,经喷嘴射入自由水域后,在极大的速度梯度作用下会产生极强的剪切力,剪切层内则会形成大量的低压旋涡,而漩涡的不断变化又会影响空化的发展过程。学者们在仿真研究空化现象时发现RANS模型难以捕捉到剪切空化,张文全[19]通过模拟与实验对比研究发现k-ε与k-ω湍流模型耦合空化模型的仿真精度较差,而大涡模拟(LES)通过分别计算大小尺度涡,能较好的捕捉剪切空化,XU[20]等、LONG等[21]以及WANG等[22]通过LES方法模拟文丘里管内部高速射流空化时,得到的空化云形态变化更明显,且模拟结果更符合实验结果。目前,关于高压水射流喷水推进装置的空化射流研究主要针对喷嘴内部流动特性及其对反推力特性的影响,对于强剪切空化的流动机理研究较少。本研究采用LES方法对推进装置的空化射流进行了仿真研究,捕捉到了推进装置喷嘴外部的强剪切空化,通过分析该空化射流的流动机理,揭示了其中空化云的形态变化规律,且在此基础上分析了进口速度对空化性能的影响,并进一步分析了空化现象对推进装置反推力特性的影响。
1 推进装置工作原理
高压水射流喷水推进装置是一种新型的船舶推进系统,主要由进水口、水液压容积式柱塞泵、喷嘴和管路等部件组成,以水为推进介质,形成了完整的能量传递和转换系统,系统原理如图1所示[7]。

图1 高压水射流喷水推进装置系统原理图Fig.1 Schematic diagram of high-pressure water jet propulsion system
通过水液压容积式柱塞泵将低速、低压、低动能的水介质转化为增压增速,并通高压管路对高能介质进行输送,经喷嘴形成高速射流喷出,从而产生反推力,推动航行器前行[18]。
由于推进装置进水口的截面积较大,水的流速较低,忽略进水口动量对反推力的影响,并将水液压容积式柱塞泵简化为恒压、恒流源,则推进装置产生的反推力为作用在推力室轴向上的静压力与动量变化的反作用力的合力,其反推进原理如图2所示[13]。反推力是高速水射流从喷嘴射出时产生的反作用力,其作用方向与航行器的运动方向一致,根据动量守恒方程,反推力可表示为:
(1)

v—— 射流的速度
p—— 压力
A—— 管路的横截面积
in,out —— 推力室入口和出口
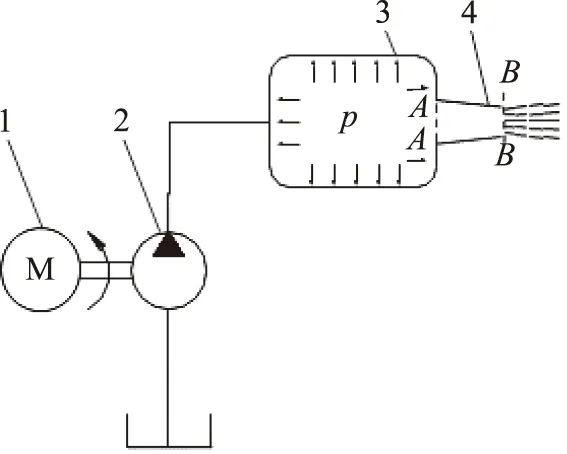
1.电动机 2.水液压容积式柱塞泵 3.推力室 4.喷嘴图2 喷射推进原理图Fig.2 Schematic diagram of water jet propulsion
再结合质量守恒方程,喷水推进装置的反推力理论计算公式可近似表示为:
(2)
其中,Cd为喷嘴的流量系数,可表示为:
(3)
式中,ρout—— 喷嘴出口处的流体密度
Δp—— 喷嘴进出口压力差
根据式(2)、式(3)可知,推力室喷嘴出口截面一定时,推进装置的反推力主要与推进室喷嘴进出口压力差以及出口的流体质量流量和密度有关,而高速空化射流的复杂流动会对喷嘴出口的流体性质产生极大的影响,因此探究空化射流的流动机理对推进装置的反推力性能具有重要意义。
2 理论模型及仿真方法
2.1 射流流体的理论模型
为探究推进装置空化射流的流动机理,本研究采用LES方法耦合Zwart-Gerber-Belamri空化模型对推进装置喷嘴产生的空化射流进行仿真分析。
1) 空化模型
Zwart-Gerber-Belamri空化模型是ZWART[23]在Kubota和Gerber模型的基础上提出的,该模型已被广泛应用,其准确性也已经得到了广泛的验证。
空化过程由传质方程控制:
(4)
式中,ρv—— 气相密度
αv—— 气相体积分数
xj——j方向坐标
m+,m-—— 蒸发和冷凝过程的传质速率
由于单位体积NB个气泡的总的传质速率为:
(5)
式中,ρl—— 液相密度
在式(5)的基础上,则可以进一步推导出蒸发和冷凝的过程:
(6)
(7)
式中,Cvap—— 汽化的经验常数,取值50
αnuc—— 成核位置处的体积分数,取值5×10-4
Ccond—— 凝结的经验常数,取值为0.01
气泡半径RB设为恒定的10-6m。以上这些常数都可以很好的预测空化流动[24-25]。
2) 控制方程和LES方法
在本研究所用的mixture模型中,各相的组成成分具有相同的速度和压力。由质量和动量守恒组成的基本控制方程如下:
(8)
(9)
式中,ui,uj——i和j方向上的速度分量
p—— 混合相压力
μ—— 层流黏度
ρ—— 混合相密度
层流黏度和混合相密度表示为:
μ=αvμv+(1-αv)μl
(10)
ρ=αvρv+(1-αv)ρl
(11)
其中,α表示混合相中组分的体积分数,下标v和l分别表示气相和液相。
将控制方程式(8)和式(9)经由Favre-filtering滤波则可以得到LES方程:
(12)
(13)
式中,上标带“-”的表示过滤量;τij表示滤波操作产生的SGS应力,为未知项,设:
(14)
并采用Boussinesq假设对SGS应力进行构建:
(15)
式中,τkk—— SGS应力各向同性的部分
μt—— SGS湍流黏度

(16)
本研究采用适应壁面的局部涡黏度(WALE)模型[26]来计算涡黏度,则μt可以表示为:
(17)

LS=min(κd,CwV1/3)
(18)
(19)
式中,κ—— 冯·卡曼常数
d—— 最靠近壁面的距离
Cw—— 默认的WALE常数,取值为0.5
V—— 计算网格的体积
2.2 仿真方法
1) 流场计算域及网格划分
本研究对推进装置的喷嘴空化流场特性以及反推力特性进行研究,将计算域简化为喷嘴和自由水域两个部分,通过SolidWorks进行三维建模,模型结构尺寸如图3所示,原点位于喷嘴进口截面的中心处,X方向为射流方向。

图3 流场模型平面图Fig.3 CFD model of water jet propulsion system
整个模型的几何尺寸如表1所示,喷嘴进口直径din为50 mm,出口直径dout为16 mm,喷嘴总长度l1为120 mm,直管段长度l0为20 mm;喷嘴外的自由水域为射流自由发展的区域,为减小边界条件对射流发展的影响,并保证计算的稳定性,将其设置为圆柱状,直径D为300 mm,长度L为100倍dout,即1600 mm。

表1 模型的几何尺寸Tab.1 Geometric dimensions of CFD model mm
本研究采用ICEM-CFD对模型进行网格划分,为了更好地捕捉流动细节,通过O-Block的拓扑方法划分了结构化网格,如图4所示,网格总数约为156万,且网格质量均在0.85以上。由于LES方法对边界层处网格的质量要求较高,且喷嘴是影响流场特性的部件,因此本研究将喷嘴壁面处的边界层网格进行了加密处理。

图4 计算域结构化网格示意图Fig.4 Structured grid of computing domain
2) 仿真设置
边界条件中,Inlet设置为速度进口,Outlet设置为压力出口,喷嘴和自由水域均设置为无滑移壁面。计算方法上,首先采用SSTk-ω湍流模型进行无空化的稳态计算,并将计算结果作为LES计算的初始流场,再进行空化的非稳态计算,其中LES方法中的亚格子模型选择WALE模型,空化模型选择ZGB空化模型,动量方程中的速度分量和压力耦合计算采用SIMPLE算法,空间离散项中,梯度项选用最小二乘法,压力项选用PRESTO!方法,动量项选用有限中心差分方法,体积分数项选用一阶迎风差分方法;而为了兼顾计算的效率和精度,时间步长设置为10-5s,每个时间步迭代30次。在所有计算过程中,各项残差均设置为10-5。
3) 准确性验证
为验证上述LES方法仿真结果的准确性,将选择进口速度为5.1 m/s的计算结果与文献[14]中对应工况的结果作对比。在前文的建模和网格划分方法下,生成了一套网格Mesh2,同时为了兼顾网格的计算效率和精度,对LES方法影响最大的边界层处的网格节点数进行了调整,生成了Mesh1和Mesh3两套网格,如表2所示为3套网格的信息,图5所示为3套网格的喷嘴出口截面。
分别将3套网格计算所得结果时均化后,与文献结果进行对比。如图6所示,为喷嘴出口外X轴线速度曲线对比图,可以发现Mesh2的结果与文献[13]中的结果更为接近,即喷嘴出口外约8倍喷嘴出口直径距离内,均为速度最大值32 m/s,随后沿X轴轴线向后以相近似的趋势逐渐减小;而Mesh1与Mesh3的计算结果与文献[14]中结果相差较大,这是由于LES方法对网格的要求极高,网格过于稀疏或者过于密集,都会降低计算精度。综上所述,采用Mesh2的网格划分方法与网格节点数兼顾了仿真的准确性和效率。

表2 3套网格信息Tab.2 Three sets of grid information

图5 3套喷嘴出口截面处网格对比图Fig.5 Comparison of nozzles’ mesh at outlet section

图6 X轴线速度曲线图Fig.6 Velocity curve at X-axis
由于本研究所研究的高压水射流喷水推进装置是在水下工作,喷嘴外自由水域的绝对压力为0.4 MPa。最终的仿真参数设置如表3所示。
3 仿真结果分析
3.1 空化射流分析
空化数是描述空化状态的无量纲参数,其与空化剧烈程度呈负相关,可由下式表示:
(20)
式中,p∞—— 液体的来流压力
pv—— 液体在相同温度下的饱和蒸气压
ρ—— 液体密度
v∞—— 液体来流速度

表3 流场仿真参数设置Tab.3 Parameter settings of CFD simulation
应用到推进装置的喷嘴处,p∞和v∞分别为喷嘴出口截面的平均值。得到的不同进口速度下的空化数如表4所示,由表可知,进口速度越大,空化数越小。

表4 不同进口速度下的流场空化数Tab.4 Cavitation number of flow field at different inlet speeds

图7 不同进口速度下空泡体积分数等值面图Fig.7 Isosurface map of cavity volume fraction at different inlet velocities
图7所示的为不同进口速度下的空泡体积分数为0.2的等值面图,选择空化发展最剧烈的时刻进行对比。结果表明,随着喷嘴进口速度的增大,空化的程度也在增强,空化发展后的空泡就越多,在轴向上的空化云长度l越长,空化云体积也就越大。
喷嘴出口之所以会产生如此多的大体积空泡,是因为当高速水射入静止的自由水域时,流动的边界层内将产生极大的速度梯度,进而产生极强的剪切力,在强剪切力作用下,剪切层内将产生大量的小尺度涡,而这些小尺度涡中心的压力较低,当其低至水的饱和蒸气压时,就会促进水中的小体积空泡膨胀,并不断发展,产生空化现象。
图8为喷嘴进口速度12.7 m/s工况下某一时刻的速度云图,由于空化射流的主体段为红色框区域内的部分,因此后续分析均在此区域内进行。

图8 速度云图Fig.8 Contour of velocity
图9为该时刻的速度云图与速度矢量图,从图中可以看出,射流核心区的速度高达138.42 m/s,而自由水域的速度几乎为0 m/s,在如此大的速度梯度下,剪切层两侧的流体发生剧烈的动量交换,出现K-H不稳定现象,形成旋涡结构。由图中标出的1~5的旋涡结构变化可以看出,小尺度涡随着射流向下游流动而不断发展,且涡与涡之间相互影响、不断合并,形成大尺度涡,进而导致射流从核心区逐渐向两侧扩散,剪切层厚度也因此在不断增加。

图9 速度云图及速度矢量图Fig.9 Contour of velocity and velocity vector
图10为同一时刻的绝对压力云图与速度矢量图,在喷嘴喉管壁面处,由于高速射流而出现低压区;在喷嘴外部,1~4号旋涡涡心处也均为低压区,压力值为3540 Pa,即为水的饱和蒸气压。
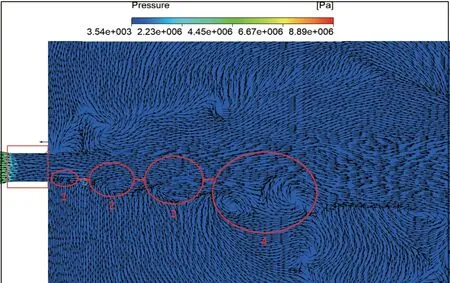
图10 绝对压力云图及速度矢量图Fig.10 Contour of absolute pressure and velocity vector
图11为同一时刻下的气相体积分数云图,空化云先从喷嘴喉管壁面处生成,在喷嘴外部,则集中分布在剪切层边界附近,而在射流核心区内部和剪切层外部并没有空化云出现,且空化云形态随着射流的发展而不断变化,由于旋涡的涡心压力为3540 Pa,在此压力下,水中的微小空泡将不断膨胀并发展,形成空化云,并随着低压旋涡逐渐变大,空化云也在不断发展,而当旋涡合并至其压力大于3540 Pa时,空化云便发展至溃灭。
图12为涡识别判据Q准则值的分布,可以发现Q值呈现正负交替变化,其中负值表示此处流体的应变占据流动的主导作用,即流体沿射流方向运动,而正值表示此处流体的旋转占据主导,即有旋涡产生,两者交替变化向下游发展,这也进一步印证了推进装置喷嘴外的空化现象产生的直接原因为强剪切力导致产生的低压旋涡。

图11 气相体积分数云图Fig.11 Contour of vapor volume fraction

图12 涡识别判据Q值分布图Fig.12 Contour of Q criterion
为了进一步探究推进装置喷嘴外空化云的形态变化,结合5个工况下空化数大小,比较分析进口速度为12.7 m/s和7.6 m/s 2个工况,两者可以分别代表强空化和弱空化的典型工况,计算结果如图13所示,从上至下6张图可以体现出空化云团在不同时刻下,因旋涡结构变化而出现的初生、发展、脱落、溃灭的形态变化全过程。以图13a中白色圈内的射流核心区一侧的空化云团为例,在t1时刻,在射流剪切层的低压旋涡内部,水中的微小空泡不断膨胀、融合,形成了肉眼可见的空化云形态,由于此时的旋涡结构较小,因此空化云体积也较小;在t2~t3时刻内,随着射流向下游的发展,剪切层逐渐变厚,其内部的旋涡结构也逐渐变大,致使涡心压力不断升高,加剧了空化云中空泡的膨胀和融合过程,空化云体积也因此逐渐增大;而在t4时刻,受到旋涡结构继续变大的影响,涡心压力进一步升高,空化云形态已经趋于不稳定,并且在整体空化云尾部已经开始有小尺度空化云脱落;在t5时刻,由于旋涡结构的合并,该侧空化云已经与另一侧空化云融合成团状,且仍存在小尺度空化云脱落的现象;在t5~t6时刻的过程中,随着旋涡结构逐渐消失,射流下游的压力逐渐增至环境压力,进而抑制空化云的进一步膨胀,导致其逐渐收缩直至溃灭。
而在射流核心区另一侧,也可以发现有与该侧空化云团不对称的空化云团以相似的过程不断变化,这是由于剪切层内的旋涡结构不对称发展而导致的。在t2时刻,喷嘴出口处已经有新的小体积空化云生成,并随着射流的发展以与下游空化云相似的规律变化,并周而复始。在图13b所示工况下,空化云的发展过程与图13a中的相似,也呈现明显的周期性变化,只是由于该工况的空化数较大,空化云尺度较小,空化的剧烈程度较弱。
3.2 反推力分析
由反推力计算公式可知,喷嘴进出口工作介质的流速、压力以及密度都是决定其大小的重要因素,而空化现象的产生会导致原本的水由单相流变为气液两相流,进而影响以上的流体性质,最终对推进装置的反推力造成影响。
为了探究空化现象对推进装置反推力的影响,本研究对5种工况进行了不考虑空化的仿真计算,将计算结果与考虑空化的进行对比,得到了表5中两种情况下在0.06 s内反推力的时均值。可以发现,无论是小空化工况下,还是剧烈空化工况下,在喷嘴进口速度一定时,考虑空化时的反推力都要比未考虑空化时的反推力要大,且随着进口速度的增大,反推力的增幅也越大。同时将仿真计算所得反推力与文献[18]中的数据进行对照,前3个工况下的反推力值与实验结果相差较小,也进一步验证了本研究计算的准确性。如图14所示,为0.06 s内不同工况下反推力值的变化曲线,可以发现,考虑空化后,虽然反推力值有所增大,但反推力的波动变化也更剧烈了。

图13 空化云形态变化图Fig.13 Contour of vapor morphologic change

表5 不同工况0.06 s内反推力时均值Tab.5 Average value of reverse thrust within 0.06 s under different working conditions
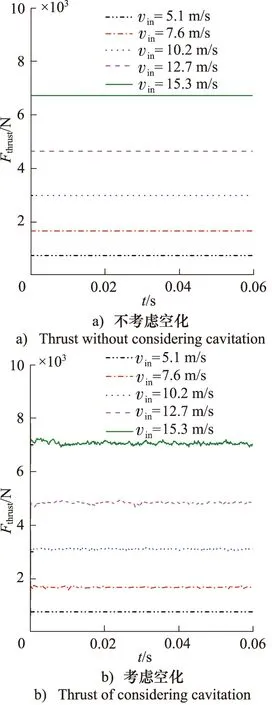
图14 是否考虑空化时的反推力变化曲线Fig.14 Comparison curve of thrust considering and without considering cavitation
由于空化现象的变化过程是连续的,喷嘴出口外空化云形态的规律性变化也会对喷嘴出口处的流体性质产生影响,进而影响推进装置的反推力。同一工况下,喷嘴进口速度和压力都是恒定的,且进出的质量流量可近似视为无变化,因此对反推力产生影响的即为喷嘴出口的压力和密度。为了进一步探究空化现象对反推力波动变化的影响,将各个工况下0.06 s内的喷嘴出口压力、密度以及反推力进行了FFT变换。
图15为喷嘴进口速度5.1 m/s工况下,FFT变换得到的结果。可以发现,压力存在明显的波动,低频的主频振幅约为1400 Pa,主频频率约为2100 Hz;而密度和反推力均无明显振幅,密度几乎全频段无波动,而反推力的振幅也只在0.03 Pa以内。结合3.1节中空化云等值面图,该工况下空化程度十分微弱,喷嘴出口压力的波动主要是由射流的波动变化导致的,而压力波动又影响反推力产生了微小波动。
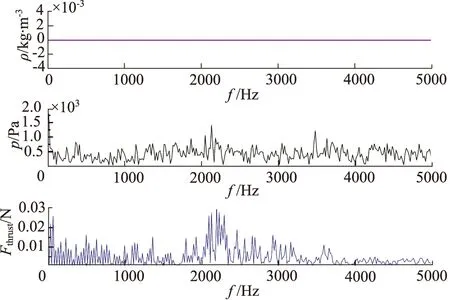
图15 进口速度5.1 m/s工况的FFT结果Fig.15 FFT results at 5.1 m/s inlet speed
图16为喷嘴进口速度7.6 m/s工况下,FFT变换得到的结果。可以发现,压力和反推力均存在明显的波动,压力的低频的主频振幅约为44000 Pa,主频频率约为316 Hz;反推力的低频的主频振幅约为7.3 N,主频频率约为515 Hz;而密度尽管存在一定的振动,但振幅最大值也才只有约0.5,此时的低频主频约为133 Hz。对照得出,反推力与压力、密度的波动趋势较为一致,尤其是与压力的波动趋势在低频段更为相似。这是由于该工况下,喷嘴出口外的空化云出现了一定的规律性形态变化,因此反推力受到了喷嘴出口压力和密度的耦合作用,出现了一定的波动,而又因为空化的剧烈程度较弱,所以压力波动依然是影响反推力的主要因素。

图16 进口速度7.6 m/s工况的FFT结果Fig.16 FFT results at 7.6m/s inlet speed

图17 进口速度10.2 m/s工况的FFT结果Fig.17 FFT results at 10.2 m/s inlet speed

图18 进口速度12.7 m/s工况的FFT结果Fig.18 FFT results at 12.7 m/s inlet speed
图17为喷嘴进口速度10.2 m/s工况下,FFT变换得到的结果。可以发现压力、密度以及反推力均存在明显的波动,且反推力与压力的波动趋势在全频段高度吻合,与密度的波动趋势在低频段也十分相似。三者的低频主频的频率均为99.8 Hz,密度波动的最大幅值约为1 kg/m3,压力波动的最大幅值约为51500 Pa,反推力波动的最大幅值约为12.4 N。在此工况下,喷嘴出口外的空化剧烈程度较大,喷嘴出口处的压力及密度受其影响也出现较大的波动变化,同时两者相互耦合,进一步影响反推力的波动。
图18为喷嘴进口速度12.7 m/s工况下,FFT变换得到的结果。可以发现,反推力与压力、密度的波动幅度在全频段均高度吻合,三者在低频的主频频率均为66 Hz,密度波动的最大幅值约为2.8 kg/m3,压力波动的最大幅值约为69400 Pa,反推力波动的最大幅值约为22.7 N。在此工况下,空化剧烈程度很强,气液两相流中,气相所占比重更大,因此密度的波动幅度也更大。相同的规律也出现在进口速度为15.3 m/s的工况下,如图19所示,喷嘴出口的密度、压力以及反推力波动的低频的主频频率均为66 Hz,密度波动的最大幅值约为4.8 kg/m3,压力波动的最大幅值约为55850 Pa,反推力波动的最大幅值约为33.4 N。
横向对比5种工况还可以发现,反推力的波动变化与喷嘴出口处的压力脉动具有很强的关联性;而与密度脉动的关联性,则随着空化程度的增强而变强。且进口速度越大,空化越剧烈,反推力波动的最大幅值越大,低频主频也越低;而在进口速度从12.7 m/s增至15.3 m/s后,由于空化剧烈程度变化较小,反推力振动的低频的主频频率并未变化。

图19 进口速度15.3 m/s工况的FFT结果Fig.19 FFT results at 15.3 m/s inlet speed
4 结论
(1) 推进装置喷嘴出口高速射流受极强剪切作用而形成了强剪切空化射流,LES大涡模拟是研究强剪切空化射流的有效方法;
(2) 推进装置喷嘴进口速度越大,出口射流速度越大,而空化数越小,空化现象剧烈。喷嘴出口高速水射流激发了不同尺度的旋涡结构,随着旋涡结构的发展演化,喷嘴出口外的空化云经历了初生、发展、不对称发展、脱落、溃灭的演化过程;
(3) 空化现象的产生会影响推进装置的反推力,在进口速度一定时,考虑空化作用影响的反推力高于不考虑空化作用的反推力,且反推力增幅随着空化程度的增强而增大;而考虑空化时反推力的脉动显著高于未考虑空化时;
(4) 推进装置的反推力受到空化云形态变化影响而呈现脉动变化,空化云形态变化是压力脉动形成的重要原因,并将使推进介质物理属性发生较大的波动,从而导致反推力产生较大的波动,反推力脉动的幅值将随空化程度的增强而增大,而脉动主频将随空化程度增强而减小。
