压力驱动的毛细管内气体流动特性数值研究
2023-01-31孙中宁谷海峰孙晓晖王一博
王 辉,邢 继,孙中宁,谷海峰,孙晓晖,王一博
(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001;2.中国核电工程有限公司,北京 100840)
压水堆核电厂严重事故期间堆芯熔化,释放大量放射性裂变产物进入安全壳,这些裂变产物主要以气溶胶的形态在安全壳内输运。当安全壳失效时,放射性气溶胶释放到外界环境,威胁公众安全。即使安全壳未被破坏,这些气溶胶也可能随气流经由混凝土安全壳缝隙、贯穿件缝隙等窄缝通道进入外界,给周边人员及环境带来影响[1]。
实验和理论研究[2-4]表明,缝隙内气溶胶存在显著的滞留,在一定情况下,气溶胶甚至会堵塞通道,从而阻止放射性的进一步释放。缝隙内气溶胶的滞留受多种机理影响,如重力沉降、布朗扩散、湍流扩散和湍流碰撞等,与缝隙内的气体流动状态密切相关。研究人员在实验和理论分析基础上总结得到了一系列基于流动参数的缝隙内气溶胶穿透系数关系式[5-8],在使用这些关系式时首先需要确定缝隙内气体泄漏率及流动特性,例如,在使用Fuchs[5]针对水平通道层流提出的气溶胶穿透系数关系式时,需要已知通道内流体的平均速度。对于毛细管类型的缝隙,工程上多采用基于层流理论推导得到的哈根-泊肃叶公式计算泄漏率[9],但核电厂严重事故下安全壳内、外两侧压差较大,缝隙内流速较高,马赫数(Ma)较大,甚至会达到壅塞状态,哈根-泊肃叶公式存在局限。Anderson等[10]分别针分子流、层流和壅塞流提出了毛细管的气体泄漏率计算公式,与实验数据的对比表明分子流和层流公式符合较好,壅塞流公式误差较大。计算流体力学(CFD)方法以其对局部流动细节的模拟能力,被研究人员广泛用于模拟压力驱动的微小通道内的气体流动[11-13],但工程应用较为不便。
本文以规则几何结构的毛细管作为缝隙代表,基于一维可压缩绝热流动方程,提出一种压力驱动的毛细管内气体流动计算方法,该方法能够模拟亚音速、临界音速及壅塞流动,并利用该方法研究毛细管两侧压差和内径对气体流动的影响。
1 控制方程及物理模型
1.1 控制方程
压力驱动的毛细管内气体流动如图1所示,数字1~5表示不同位置。其中1为毛细管上游容器处;5为毛细管下游环境,上游容器压力高于下游环境,驱动气体在毛细管内部形成流动;2为毛细管入口处,从1到2流动有入口形阻压降;3和4为毛细管出口,从3到4流动有出口形阻压降;毛细管内部从2到3流动有沿程摩擦阻力压降。

图1 压力驱动的毛细管气体流动示意图Fig.1 Sketch of pressure-driven gas flow in capillary
假定毛细管与外界绝热,当流动的克努森数Kn小于0.001时,流体为连续介质,可采用一维等截面通道内有摩擦阻力的绝热流动方程描述:
(1)
式中:p为压力,Pa;f为范宁阻力系数;DH为水力直径,m;ρ为流体密度,kg/m3;v为流体速度,m/s;x为一维方向上的距离,m。
马赫数Ma如下:
(2)
式中:γ为气体绝热指数;R为气体常数,N·m/(kg·K)。
结合式(2)和理想气体状态方程p=ρRT,式(1)可以变为:
(3)
p和温度T也可写为Ma的函数,如下:
(4)
(5)
式(3)~(5)组成了毛细管内一维绝热流动的控制方程组。
在毛细管入口(x=0)处,有:
T=T0,p=pstg
(6)
式中:T0为滞止温度,K;pstg为滞止压力,Pa。
在毛细管出口(x=L)处,有:
p=pL,MaL≤1.0
(7)
式中:pL为出口处的压力,Pa;MaL为出口处的马赫数。
1.2 阻力系数关系式
对于毛细管等微小通道内的流动阻力,气体稀薄性减弱了通道的阻力系数,而气体密度变化导致的流动加速则增大了阻力系数,这两种效应的耦合作用使得阻力系数实验结果偏离度较大。本文考虑毛细管内气体为连续流动的情形,未包括过渡流和分子流,因此计算层流阻力系数时选择了经典的层流阻力关系式进行计算;在计算湍流阻力系数时,文献[14]开展的实验数据对比显示光滑管情况下Blasius关系式符合较好,而粗糙管时则Colebrook关系式符合较好。在层流向湍流转捩方面,文献[15]根据实验结果认为微小通道内的转捩点(以雷诺数Re表征)存在提前的情况,某些情况下阻力系数转捩点甚至可以提前到500~600;但文献[16-18]则指出在各自的实验中并未发现转捩点提前,本文计算时考虑阻力系数转捩点仍为2 100。这样,本文选用的阻力系数关系式如下。
当雷诺数Re小于2 100时,有:
4f=64/Re
(8)
当雷诺数Re大于2 100时,有:
(9)
式中:D为毛细管直径,m;ε为绝对粗糙度,m。
2 数值求解方法
上述控制方程中,阻力系数与雷诺数有关,进而与流体温度有关,流体温度又取决于流动状态,因此无法直接求解。本文采用如下方法进行求解。
对式(3)、(4)从位置i到位置j进行积分,有:
(10)
式中,Kij为从位置i到位置j的阻力系数。
(11)
将式(10)、(11)应用于图1的位置1~4,可得到6个方程,其中p1和p5已知,根据文献[19],K12可取0.5,K34可取1.0。
当流动为亚音速和临界音速时,p4=p5,Ma4≤1.0。初始假定Ma4=0.001,则p2、p3、Ma1、Ma2、Ma3、K23未知,方程组封闭,可以求解。依次以较小的幅度增大Ma4直至1.0,从而得到已知p1和p5下的若干组可能的亚音速和临界音速流动状态参数(p2~p4,Ma1~Ma4和K23)。
当流动为壅塞流时,p4>p5,Ma4=1.0。初始假定p4为稍大于p5的数值,此时未知的物理量仍为p2、p3、Ma1、Ma2、Ma3、K23,可以求解。依次以较小的幅度增大p4直至K23=0.0,同样可以得到已知p1和p5下的若干组可能的壅塞流动状态参数(p2~p4,Ma1~Ma4和K23)。
针对每组可能的流动状态参数,将Ma3-Ma2均分成N份(N由节点敏感性分析确定),每一份即为微分方程(3)~(5)的有限差分单元。第i个差分单元有如下方程:
(12)
(13)
Δx采用下式计算:
(15)
式中,Δx为差分单元的长度,m。
毛细管的总长度L为:
(16)
毛细管内质量流量m为:
(17)
这样,在已知毛细管直径和绝对粗糙度后,针对每组可能的流动状态参数,均可以计算得到相对应的毛细管长度和毛细管质量流量。在此基础上,采用毛细管实际长度进行插值,即可得到实际的质量流量及流动状态参数。采用FORTRAN语言编制计算程序实现该数值求解方法,计算流程如图2所示。

图2 计算流程图Fig.2 Computational flow diagram
3 数值计算方法的验证
为测量微小通道的阻力系数,日本鹿儿岛大学开展了毛细管流动特性实验[20-21],实验涵盖了低压和高压工况,具有较好的代表性,因此采用该实验验证数值计算方法。另外,考虑到实验监测点有限,无法得到毛细管内所有位置的流动信息,因此,本文也采用三维CFD方法对实验进行数值模拟,模拟结果亦用于数值方法的验证。
3.1 实验简介
鹿儿岛大学研究团队采用的实验装置如图3[20]所示。实验采用的工质为氮气,温度为300 K。实验时将氮气注入毛细管上游容器从而在毛细管内部形成压力驱动的流动,毛细管下游环境压力为100 kPa。毛细管为光滑玻璃管,长度120 mm,直径397 μm,相对粗糙度为0.002%[21]。实验采用流量计测量通过毛细管的质量流量,为得到毛细管内部的压力、温度及马赫数分布,分别在距离入口0.09、0.10、0.11 m处钻小孔进行测量。
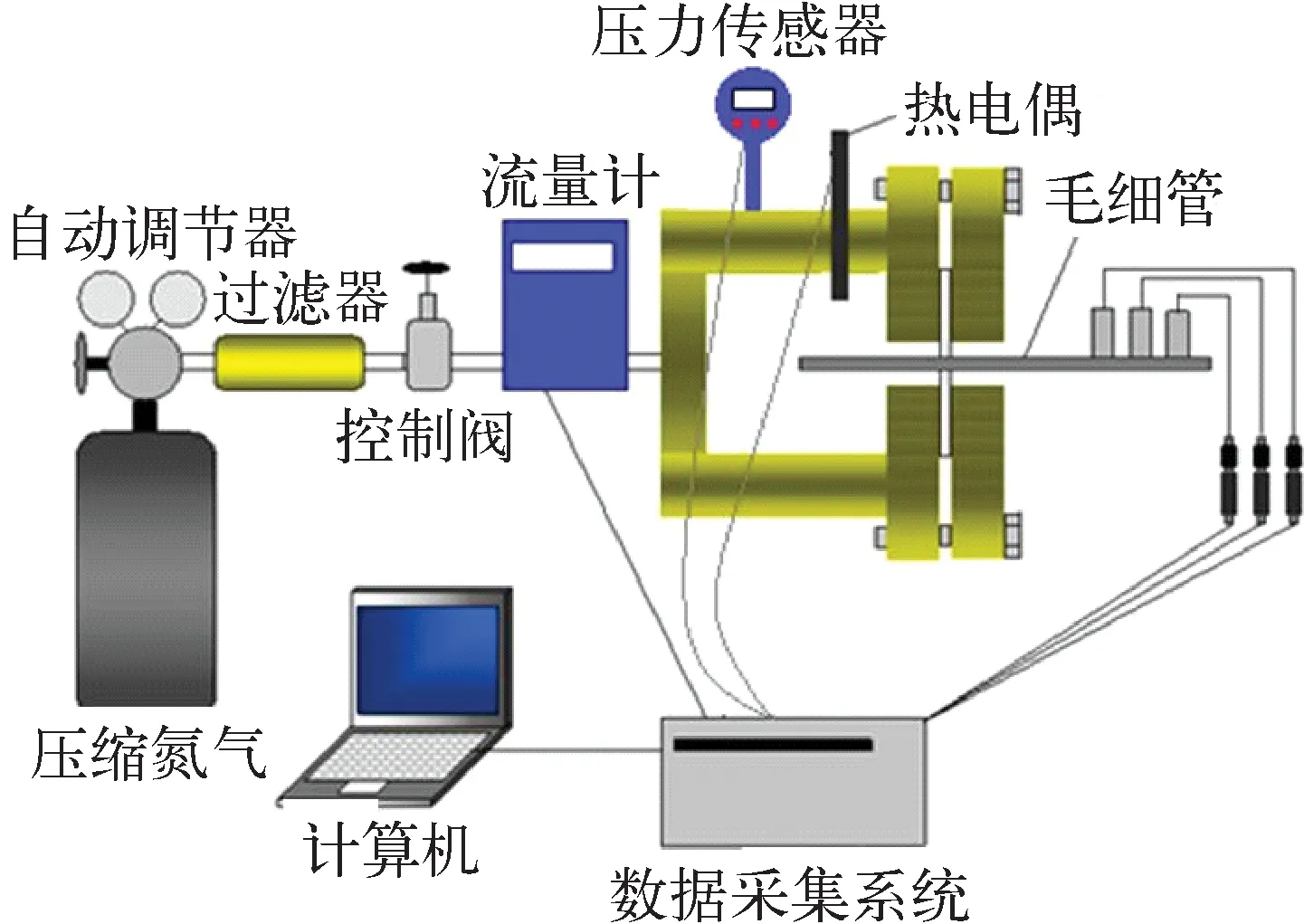
图3 毛细管流动特性实验装置Fig.3 Experimental setup for flow characteristic through capillary
3.2 CFD模型
采用ANSYS Fluent 19.2对鹿儿岛大学的毛细管流动特性实验建模计算,CAD模型如图4所示,模型将毛细管上游和下游均处理为圆柱形容器,容器直径和长度远大于毛细管直径,从而消除了容器对毛细管内部流动的影响。
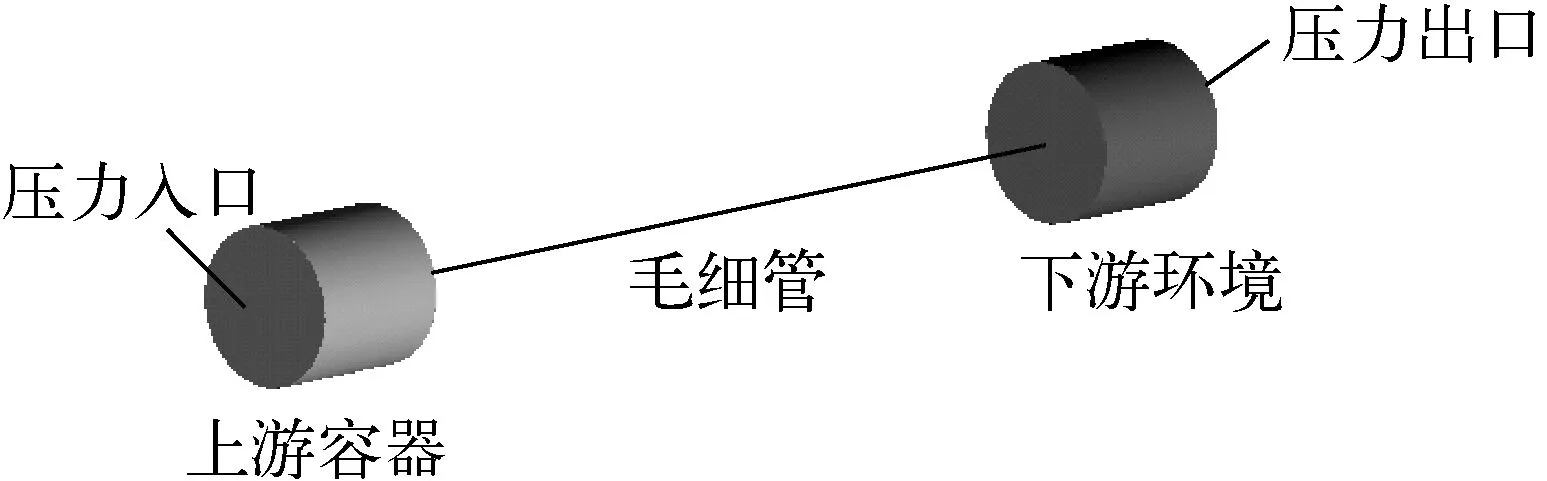
图4 毛细管流动特性实验装置的CAD模型Fig.4 CAD model for experimental setup for flow characteristic through capillary
采用ICEM CFD软件对CAD模型进行网格划分,生成结构化网格。经网格敏感性分析,最终选取了网格数量约为170万的划分方案。在前处理中分别为模型设置压力入口与出口,如图4所示,压力入口处的压力即为容器内部的滞止压力;压力出口取外界环境压力1个大气压。采用理想气体状态方程计算氮气密度。湍流模型选取了SSTk-Ω模型,与标准的k-ε模型相比,该模型直接求解黏性层,不需要壁面函数,但需在边界层内布置一定密度的高质量网格。经计算,本文的边界层网格Y+约为2,满足模型适用要求。
3.3 对比分析
利用本文提出的一维数值计算方法和CFD模型对上游滞止压力为200 kPa的实验工况进行计算。图5示出了一维方法、CFD模型计算得到的压力、温度及马赫数沿管长分布与实验的对比。可以看出,沿着管长方向,在摩擦阻力作用下,气体压力下降,密度减小,流动加速,温度降低。图6、7中毛细管不同位置的速度和温度云图更直观地示出了流动加速和温度降低的过程。由图5可看出,在x=0.09,0.10,0.11 m位置处,两种方法的计算结果与实验较为接近,其中一维方法得到的压力、温度和马赫数与实验值的最大偏差分别为5.1%、1.4%和10.0%,CFD模型得到的压力、温度和马赫数与实验值的最大偏差分别为4.7%、0.6%和12.0%,一维方法与CFD方法精度相当。在管长方向上,一维方法与CFD模型变化趋势一致,偏差在4.0%以内。另外,该工况下实验测得的质量流量为1.966 96×10-5kg/s,一维方法和CFD模型对应的质量流量分别为1.834 42×10-5kg/s和1.703 00×10-5kg/s,3种方法的质量流量比较接近,但CFD模型与实验数据的相对偏差较大。

图5 滞止压力200 kPa时的压力、温度与马赫数沿管长的分布Fig.5 Distribution of pressure, temperature and Mach number along capillary length at stagnation pressure of 200 kPa
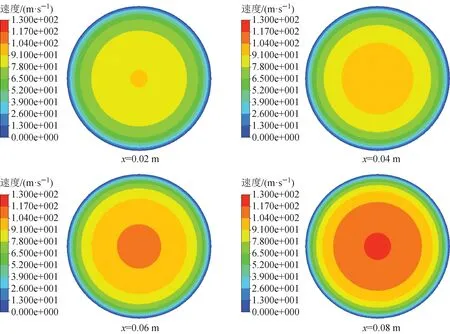
图6 毛细管内部不同位置处的速度云图Fig.6 Velocity contour at different locations in capillary
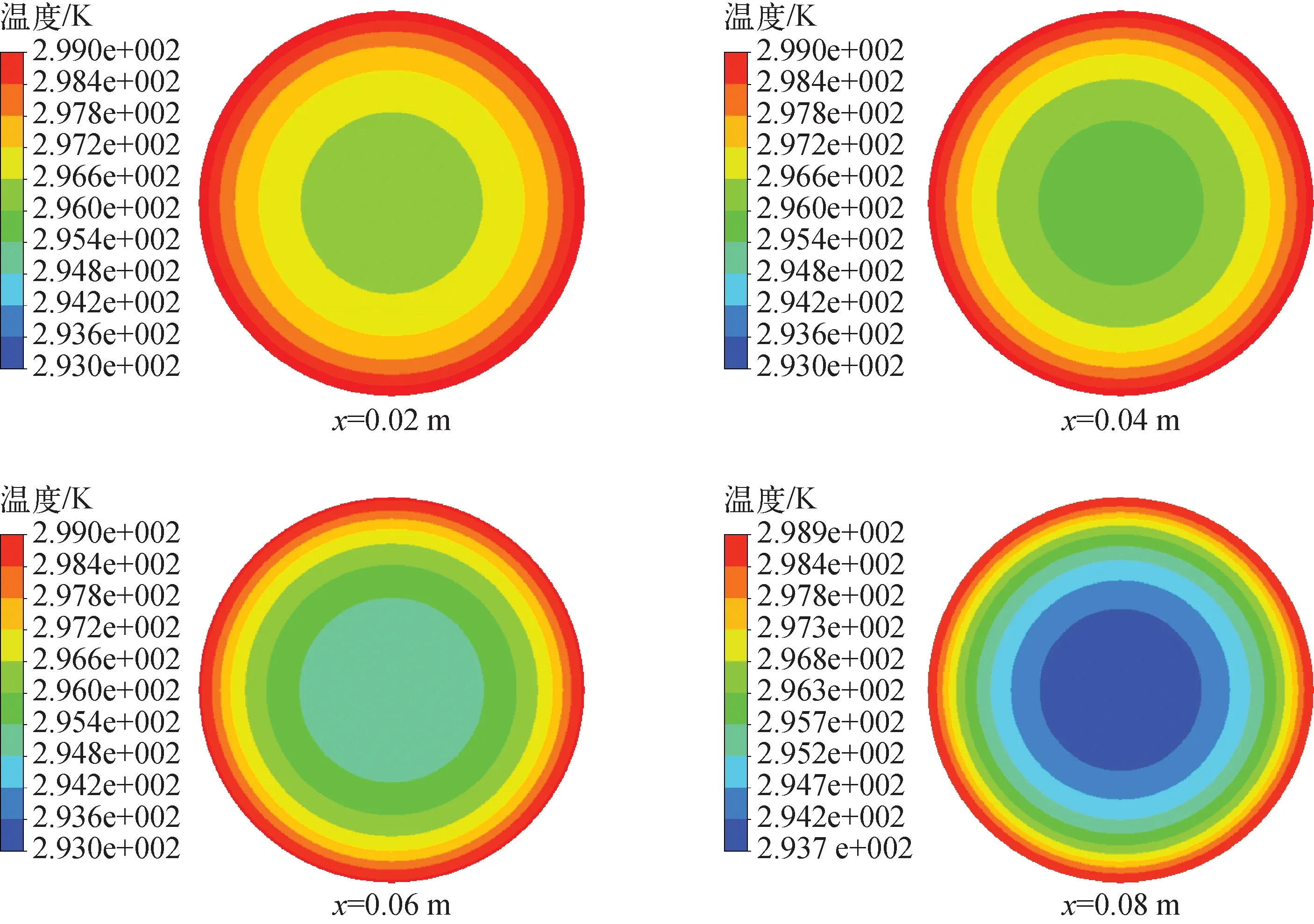
图7 毛细管内部不同位置处的温度云图Fig.7 Temperature contour at different locations in capillary
采用一维方法对更多实验工况进行计算,图8示出不同滞止压力下毛细管质量流量、压力及马赫数与实验的对比。可看出,一维方法很好预测了质量流量及毛细管内部压力分布,其中质量流量计算结果与实验值在滞止压力为150 kPa时偏差为11.16%,偏差较大,其余偏差均在3%以内;压力偏差均小于3%,马赫数分布的计算结果与实验值的偏差和质量流量与压力的偏差相比较大,但绝大部分偏差小于10%。产生这种偏差可能的原因在于,本文计算时考虑为绝热条件,文献未详细说明毛细管试验件的温度控制措施及结果,温度偏差导致了密度偏差,进而造成了马赫数的偏差。
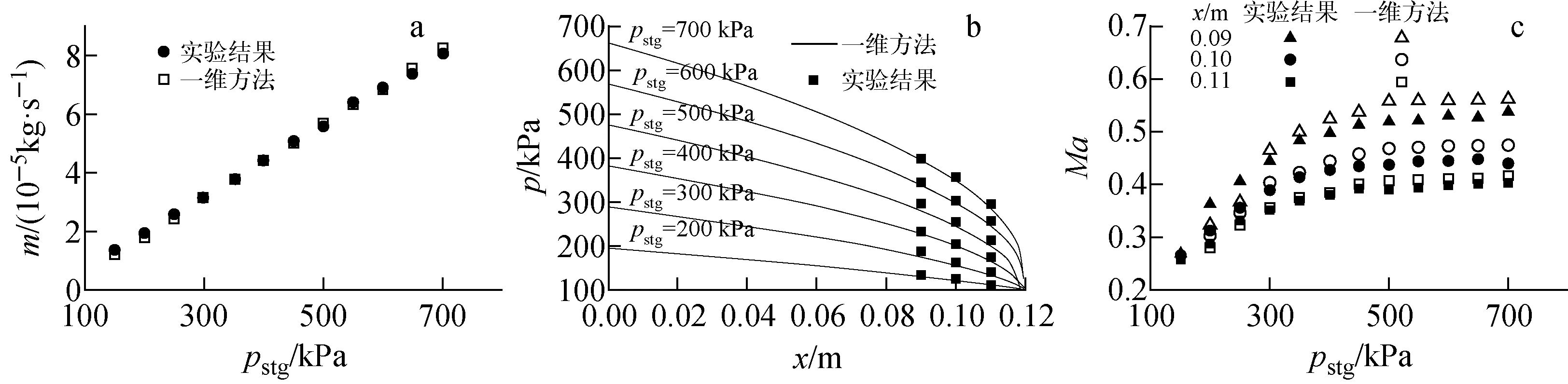
图8 计算结果与实验值的对比Fig.8 Contrast of calculated and experimental results
基于鹿儿岛大学开展的毛细管流动实验以及本文建立的CFD模型的验证结果表明,本文开发的一维计算方法可在大的压差范围内分析计算不同内径的毛细管内压力驱动的气体流动。与CFD方法相比,一维方法计算效率很高,1个工况的计算时间约为5 s,而CFD模型在使用24核达到收敛解时所需的时间约6 h。
4 毛细管内径及两侧压差对流动的影响
鹿儿岛大学开展的毛细管流动特性实验虽然涵盖了低压和高压情形,但毛细管内径单一,本文采用经验证的一维计算方法开展了不同内径和压差下的毛细管流动计算,以研究流动的变化规律。图9示出了不同内径的毛细管内压力驱动的气体质量流量随上游滞止压力的变化,并结合图8进行分析。
由图8c可看出,在下游背压不变的情况下,随着上游滞止压力的提高,两侧压差增大,管长各处的马赫数逐渐增大。但当滞止压力超过某一数值时(图8c约为400 kPa),管长各处的马赫数基本不再变化,表明流动处于壅塞状态。虽然x=11 cm处距出口仅为1 cm,但受该1 cm段摩擦损失及出口形阻损失作用,马赫数稳定在0.54左右,不能达到1.0。另外,在流动达到壅塞状态后,虽然马赫数不再随滞止压力的提高而增大,但滞止压力的提高增大了气体密度,因而通过毛细管的质量流量随滞止压力的提高持续增大,如图8a和图9所示。
进一步分析图9,当毛细管内径小于100 μm时,随压差的增大气体质量流量近似呈二次方增长,而当内径大于100 μm时,压差超过某一数值后质量流量增长趋势向线性化过渡。其原因在于,在本文计算的压差范围内,小内径毛细管处于层流状态且气体压缩性不显著(以25 μm毛细管为例,雷诺数介于8~20,出口马赫数介于0.004~0.06),这样沿程气体温度降幅较小,经典的哈根-泊肃叶公式完全适用,因此泄漏流量随压差的增加近似呈二次方增长。
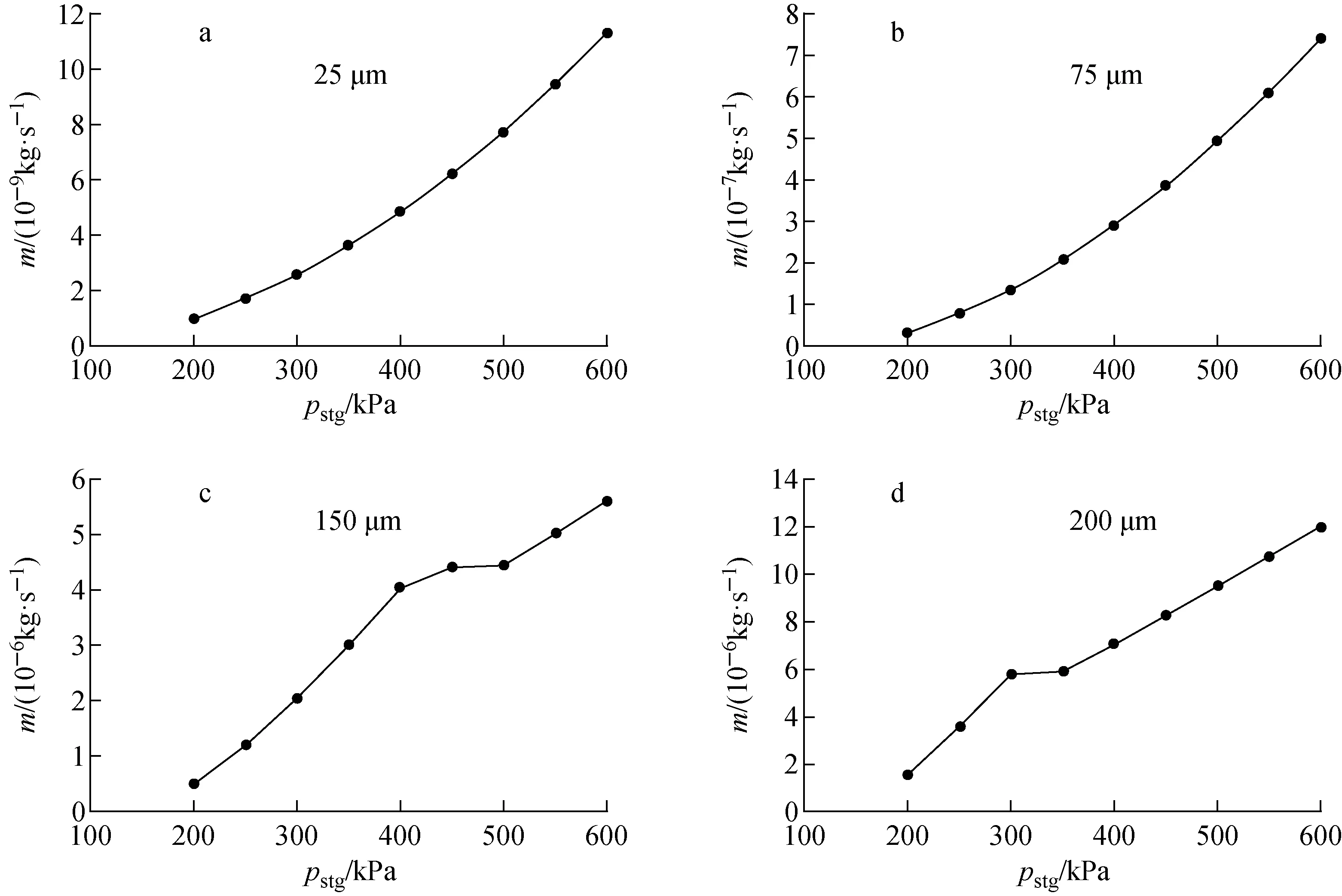
图9 不同内径的毛细管内质量流量随滞止压力的变化Fig.9 Variation of mass flow rate with stagnation pressure in capillaries with different inner diameters
对毛细管内径较大的情况,随压差的增大,毛细管内部流态会从小压差的层流到大压差的湍流转变,马赫数也逐渐增大,气体压缩性显著,哈根-泊肃叶关系式不再适用。
注意到,对于150 μm和200 μm的情形,在泄漏流量由二次方增长变为线性增长时,均出现了流量平台,平台范围内随压差的增大流量只有小幅增大或基本不变。以150 μm为例,质量流量平台出现在滞止压力350~450 kPa。图10示出沿程摩擦阻力系数K23随滞止压力的变化,由图10可见,随着滞止压力的提高,阻力系数首先下降,在350~450 kPa范围内,阻力系数增大,之后又呈下降趋势。根据这种阻力变化趋势,可推断随着滞止压力的提高,泄漏流量首先增大,在平台区内,滞止压力提高导致气体流速增大,流速增大又造成阻力系数增大,因此泄漏流量只有小幅增长或基本不变,当跨过平台区后,泄漏流量随滞止压力的提高而逐渐增大。进一步分析如图11所示的平台区雷诺数,可看到随滞止压力的增大,雷诺数增大,但均位于层流到湍流的过渡区。根据经典的阻力系数莫迪图[19],在过渡区阻力系数随雷诺数的增大而增大,证明了前述分析的合理性。
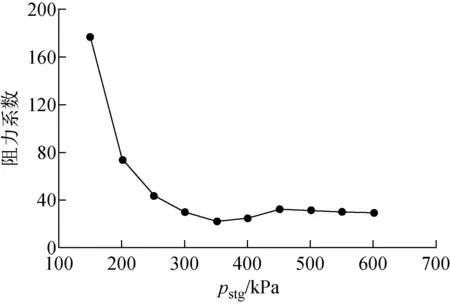
图10 阻力系数随滞止压力的变化Fig.10 Variation of friction coefficient with stagnation pressure
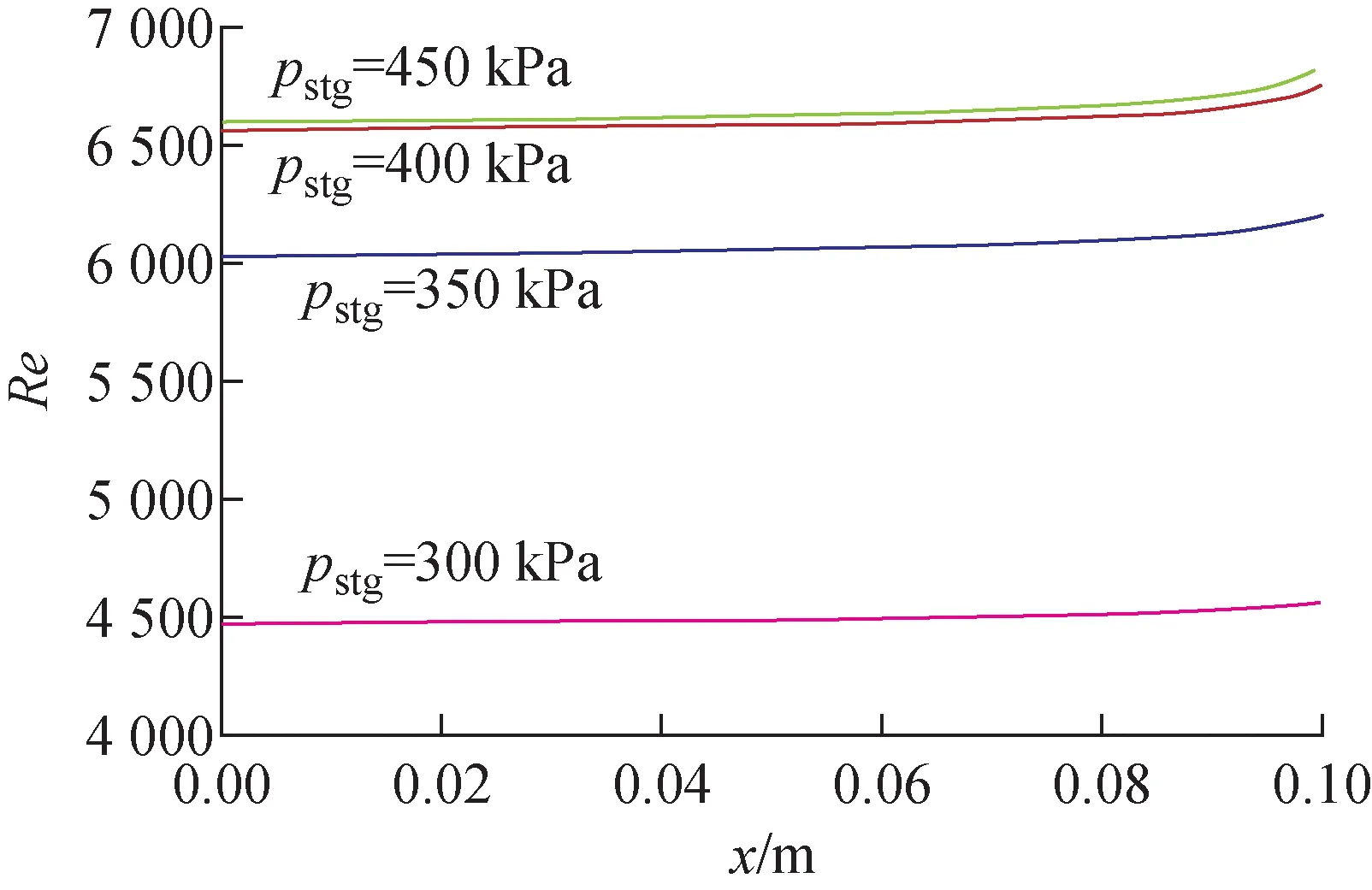
图11 不同滞止压力下雷诺数沿管长的分布Fig.11 Distribution of Reynolds number along pipe length under different stagnation pressures
比较图9c和d,可发现,200 μm情形下流量平台要早于150 μm,原因在于毛细管内径越大,相同滞止压力下的雷诺数越大,因此层流到湍流的过渡区越早出现。当毛细管内径增大到一定程度时,质量流量平台几乎消失,如图8a所示。
5 结论
1) 针对压力驱动的毛细管内气体流动,本文基于一维可压缩绝热方程开发了一种数值计算方法,能够计算压力驱动的毛细管内亚音速、临界音速与壅塞流动。经过与鹿儿岛大学开展的毛细管流动特性实验和CFD数值模拟结果对比,流动趋势一致,偏差较小,验证了一维数值计算方法的准确性与可靠性。与CFD数值模拟方法相比,该方法大幅提高了计算效率。
2) 采用本文开发的数值方法分析了毛细管两侧压差与内径对泄漏特性的影响,结果表明小内径毛细管的泄漏流量随压差的增大呈二次方增长,而当内径大于100 μm时,压差超过某一数值后质量流量增长趋势向线性化过渡。当压差使得流动处于层流和湍流过渡区时,受阻力系数变化趋势影响,泄漏流量会出现一个平台,内径越大,则平台出现越早。
3) 本文数值计算方法的开发为基于气溶胶穿透系数关系式的气溶胶泄漏与滞留分析奠定了技术基础。针对严重事故后安全壳内高温、高湿的热工环境,后续将拓展该方法至压力驱动的毛细管内多组分气体流动的计算分析。
