基于粒子群优化算法的有轨电车节能研究*

侯宇婷 蔡煊

成都工业学院 汽车与交通学院 四川 成都 611730

引言

随着城市交通的快速发展，有轨电车因具有安全、舒适、成本低和环保等优点，成为解决城市交通拥堵和环境污染等问题的重要交通工具，特别是在大城市郊区、中小城市城区和旅游景区等地。截至2021年12月31日，我国内地共有约20座城市开通运营了约36条有轨电车线路，工程长度为454km，运营里程达504km，占城市轨道交通总运营线路里程的5.47%，位列第三。近10年来，有轨电车运营里程实现了约5倍的增长。

随着有轨电车的广泛应用，随之而来的能耗问题也日益凸显。由于有轨电车缺乏有效节能优化方案，使得其在运行过程能耗较大，占运营成本的比例较高，不仅对节约能源、建设节约型城市提出严峻挑战，而且直接增加企业运营成本和地方政府财政补贴负担[1]。同时，随着“碳达峰”、“碳中和”理念的提出，节能减排问题日渐受到重视。因此，有必要从节能优化角度对有轨电车运行过程进行研究，降低能耗成本。

目前，针对有轨电车节能优化的系统性研究较少。研究学者提出基于最小二乘支持向量机回归的有轨电车能耗预测模型，设计了现代有轨电车节能管理系统[2]。针对无接触感应供电有轨电车，研究学者建立了基于NSGA-Ⅱ的多目标遗传算法节能优化模型[3]。以武汉某有轨电车线路为研究对象，分析该线路运行所需的能耗结构，并提出节能措施[4]。针对半独立路权下有轨电车，研究学者以模糊数学规划为基础构建了以减小列车总旅行时间和总能耗为目标的有轨电车节能优化模型[5]。针对储能式有轨电车，研究学者建立了单区间速度曲线优化模型，采用基于NSGA-II的多目标遗传算法进行求解[6]。在总牵引能耗最小优化方面，研究学者建立了时刻表和列车操纵双层节能优化模型[7]。针对半独立路权下有轨电车信号被动优先控制，研究学者了建立时刻表和操纵节能优化双层模型，设计混沌遗传算法进行求解[8]。

目前，有轨电车节能的研究多针对特定的场景或特定的运行阶段，综合性的节能策略研究较少。由于有轨电车能耗模型需要满足运行距离、运行时间和线路限速等多约束的要求，操纵策略搜索过程复杂，传统方法难于建立精确的搜索模型。粒子群优化算法在轨道交通高铁和地铁列车节能中进行了广泛的研究，并取得了较好的效果[9-12]，但在有轨电车节能方面尚未展开深入研究。本文将粒子群优化算法引入到有轨电车节能优化研究领域，构建单列车节能运行控制模型，提出以节能优化为目标函数，满足多约束的有轨电车节能操纵策略模型，解决有轨电车节能优化的问题。

1 问题描述

有轨电车从当前车站出发，运行到下一车站停站的过程中，施加的控制工况包含牵引、巡航、惰行和制动4种。运行过程中施加的控制工况及其对应的运行距离的有序集合称为列车驾驶操纵策略。有轨电车每一种操纵策略均对应了一个牵引能耗和运行时间，在指定的运行距离、运行时间和线路条件下，存在至少一组操纵策略，使得有轨电车在站间运行花费的总能耗最少，该组操纵策略即为指定运行距离、运行时间和线路限速下的最优操纵策略。所有最优操纵策略对应的“能耗-时间”如图1所示。

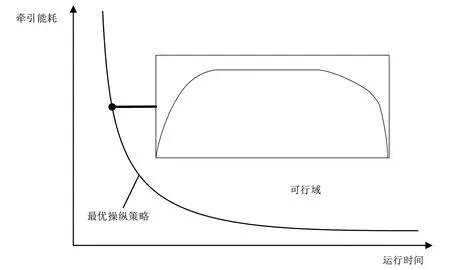
图1 有轨电车最优操纵策略

有轨电车节能运行是一个典型的多约束的优化问题，即在指定的运行距离、运行时间和线路条件等情况下，寻找最优操纵策略使列车的能耗最少。由于有轨电车运行的复杂性，难以建立精确的数学模型描述列车的运行过程。

2 有轨电车操纵策略

站间运行过程中，有轨电车节能操纵主要采用4阶段运行模型：牵引-巡航-惰行-制动，如图2所示。

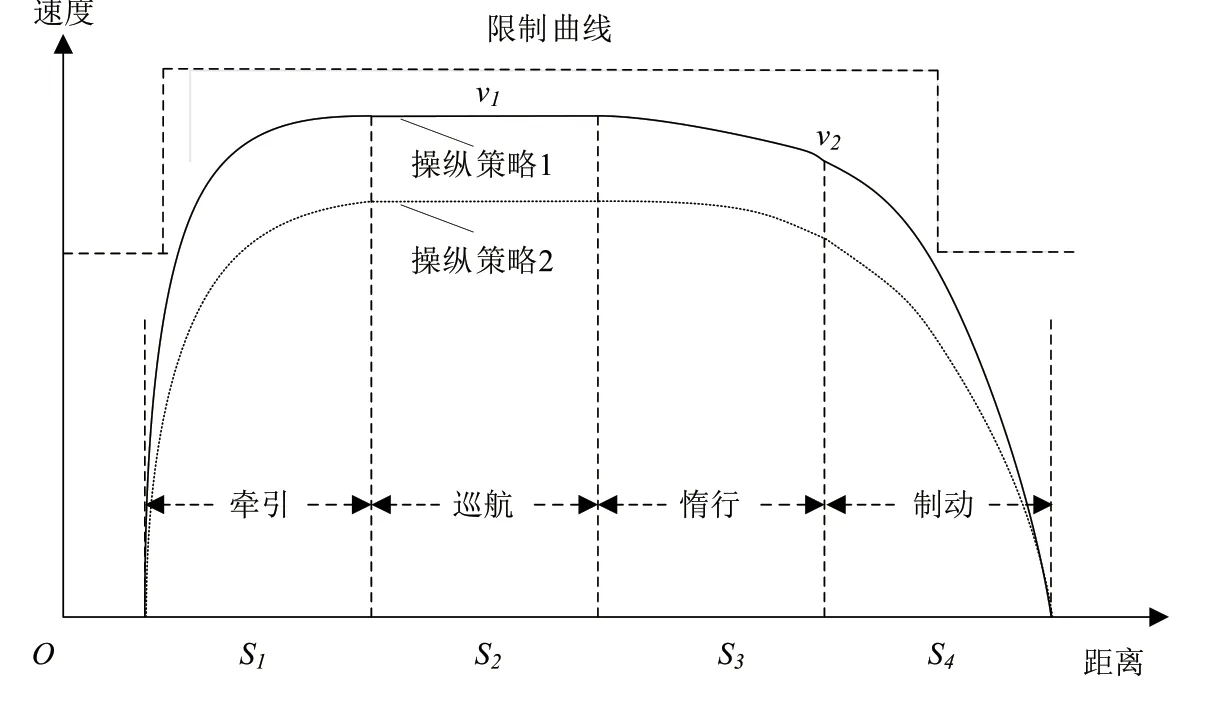
图2 有轨电车4阶段操纵策略

在运行距离、运行时间和线路限速一定的条件下，列车从当前车站运行至下一车站的过程中，存在多种能够同时满足这些约束条件的运行操纵方案，不同状态的牵引、巡航、惰行和制动操纵直接对列车运行能耗产生不同的影响。不同驾驶经验的司机在同一条线路上执行相同的行车计划时，列车运行花费的能耗可能差异很大。如图2，列车在站间分别采用2种操纵策略，操纵策略1和操纵策略2均采用牵引、巡航、惰行和制动操纵4种操纵方式，但在巡航速度和惰行结束时的速度方面选择不同，两种操纵策略的运行距离均为S1+S2+S3+S4，但运行时间不同，所消耗的能耗不同。根据研究，不同操纵策略在同一线路上运行时造成的能耗差异可达30%[13]。

目前，考虑到灵活性等因为，有轨电车司机通常采用两段巡航的操纵策略，包括牵引、巡航和制动3种运行工况，典型的运行操纵速度曲线如图3所示[14]。列车先以加速度a1牵引到速度v1，然后保持v1速度巡航S2；然后以减速度a2减速到v2，保持v2速度巡航S4；最后以减速度a2减速到0。列车节能优化问题可转化为确定合适的2次巡航速度v1、v2及各个阶段的运行距离，使得列车在S1、S2、S3、S4运行的总能耗最小。

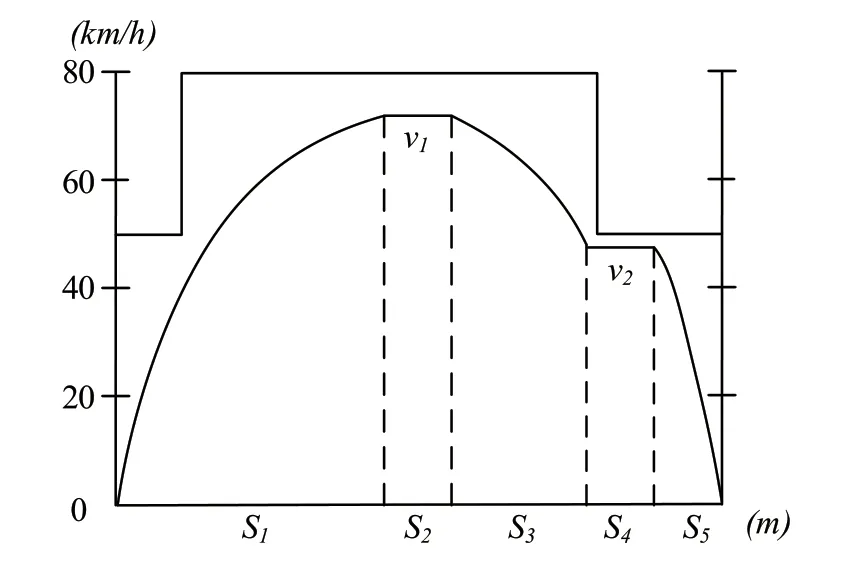
图3 有轨电车两段巡航操纵策略

3 粒子群优化算法

粒子群优化（Particle Swarm Optimization， PSO）算法是美国社会心理学家Kennedy和电气工程师Eberhatr受自然界鸟类寻找食物的过程启发在1995年提出的一种智能优化算法。PSO具有调整参数少，求解容易，搜索速度快等优势，能够在搜索过程不断累积经验，在整体上朝着最优解的方向进行搜索。目前，PSO算法已经广泛应用于解决多目标优化、控制器参数优化、带约束优化和调度规划等问题。

PSO算法中，粒子表示潜在的解，其通过历史位置、速度和群体信息来确定运动过程，搜寻目标函数的最优解。PSO算法求解主要包括以下求解过程[15]：①在速度空间和可行解空间内，对每个粒子的位置和速度进行随机初始化；②在算法每次的搜索迭代过程中，计算每个粒子的适应度函数值，计算并更新每个粒子的个体最优位置、整个种群的全局最优位置，并依据这两个最优位置对每个粒子的速度和位置进行更新；③若未达到停止条件，转步骤2；否则停止算法，输出当前最好结果，实现问题的应用求解。

PSO算法参数设置如下：

n维搜索空间内粒子i的位置为xi=(x1,x2,…,xn)。

n维搜索空间内粒子i的速度为vi= (v1,v2,…,vn)。

在n维搜索空间内粒子的个体最优位置为：pi= (p i1,pi2,…,pin)。

在n维搜索空间内种群全局最优位置为：pg= (p g1,pg2,…,pgn)。

承诺执行AEOI的经济体正通过多边税收信息自动交换机制，参与到改善全球金融账户涉税信息透明度的协同性行动中来。大约到2018年底，随着有关经济体承诺的执行AEOI的时间表到来，执行AEOI的经济体都将掌握本国居民的全球金融账户涉税信息，一个涉及自然人和法人全球所得的税收透明时代即将来临。

在n维搜索空间内找到粒子的个体最优位置和种群全局最优位置后，根据PSO算法更新优化的思想，采用式（1）和式（2）对种群内每个粒子i的速度和位置进行迭代寻优。

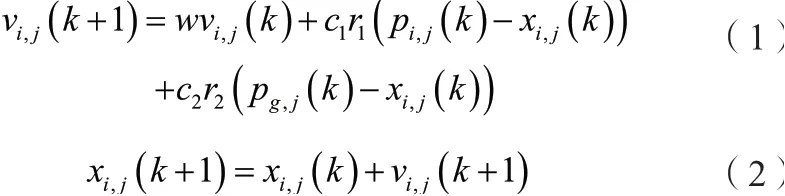
其中，w表示粒子的惯性权重系数，c1、c2为常数因子，表示粒子的局部收敛能力和全局收敛能力，r1、r2为取值范围在[0,1]内的随机数；v i,j(k)和x i,j(k)为第k次迭代时粒子i的当前速度和当前位置；p i,j(k)和p g,j(k)为第k次迭代时粒子i的个体最优位置和种群的全局最优位置。

4 基于PSO的有轨电车节能优化

本文将有轨电车列车作为单一质点进行研究[16]。基于PSO的有轨电车节能优化以减少列车站间运行过程中的能耗为目标，保证列车从起始点出发，初速度v0= 0，在运行距离、运行时间和线路限速的约束下，使列车运行距离S后到达终点站停车，所用时间为T，即vT= 0。

本文以图3所示的有轨电车当前广泛采用的两段巡航操纵策略为研究基础，采用PSO算法构建单列车节能优化模型，在指定运行距离、运行时间范围、速度限制和边界速度条件的约束下，实现列车耗能最小的目标。有轨电车能耗包括牵引阶段、巡航阶段和制动阶段3部分能耗。

4.1 牵引阶段的能耗

有轨电车牵引阶段的能耗为牵引力做功，速度变化影响列车基本阻力的大小，进一步影响车辆牵引力的大小。牵引阶段能耗的计算公式如下：

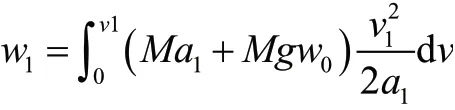
其中，M为有轨电车质量，g为重力加速度，w0为列车单位基本阻力。

4.2 巡航阶段的能耗

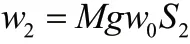
4.3 制动阶段的能耗

有轨电车制动阶段的列车能耗为制动力做功，速度变化影响制动力的大小，计算公式如下：

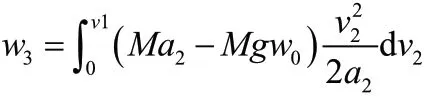
由于站间运行距离S=S1+S2+S3+S4，为描述方便，将S4用其他几个阶段的距离进行表示，即考虑到有轨电车运行时间范围的要求，既不能晚点也不能早点太多，影响时刻表计划。同时，为保持有轨电车两段巡航操纵策略的可扩展性，研究对操纵策略进行灵活扩展，允许2阶段的巡航速度相等。有轨电车节能优化研究目标及约束条件如下：

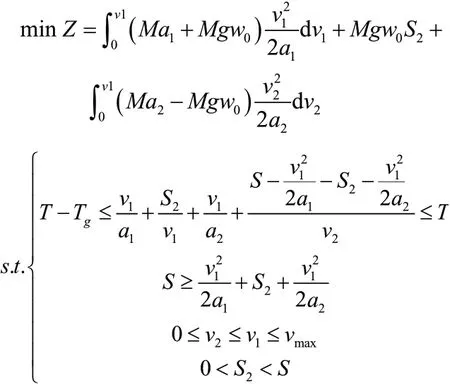
其中，Z为有轨电车运行过程中总的能耗值；v1为1阶段巡航速度，v2为2阶段巡航速度，vmax为线路限速，a1为加速度；a2为加速度，Tg为允许早点时间。

有轨电车节能优化问题可将约束条件转换为以v1，v2，S23个参数为自变量的优化问题求解。

基于PSO的有轨电车节能的具体的算法流程图如图4所示。

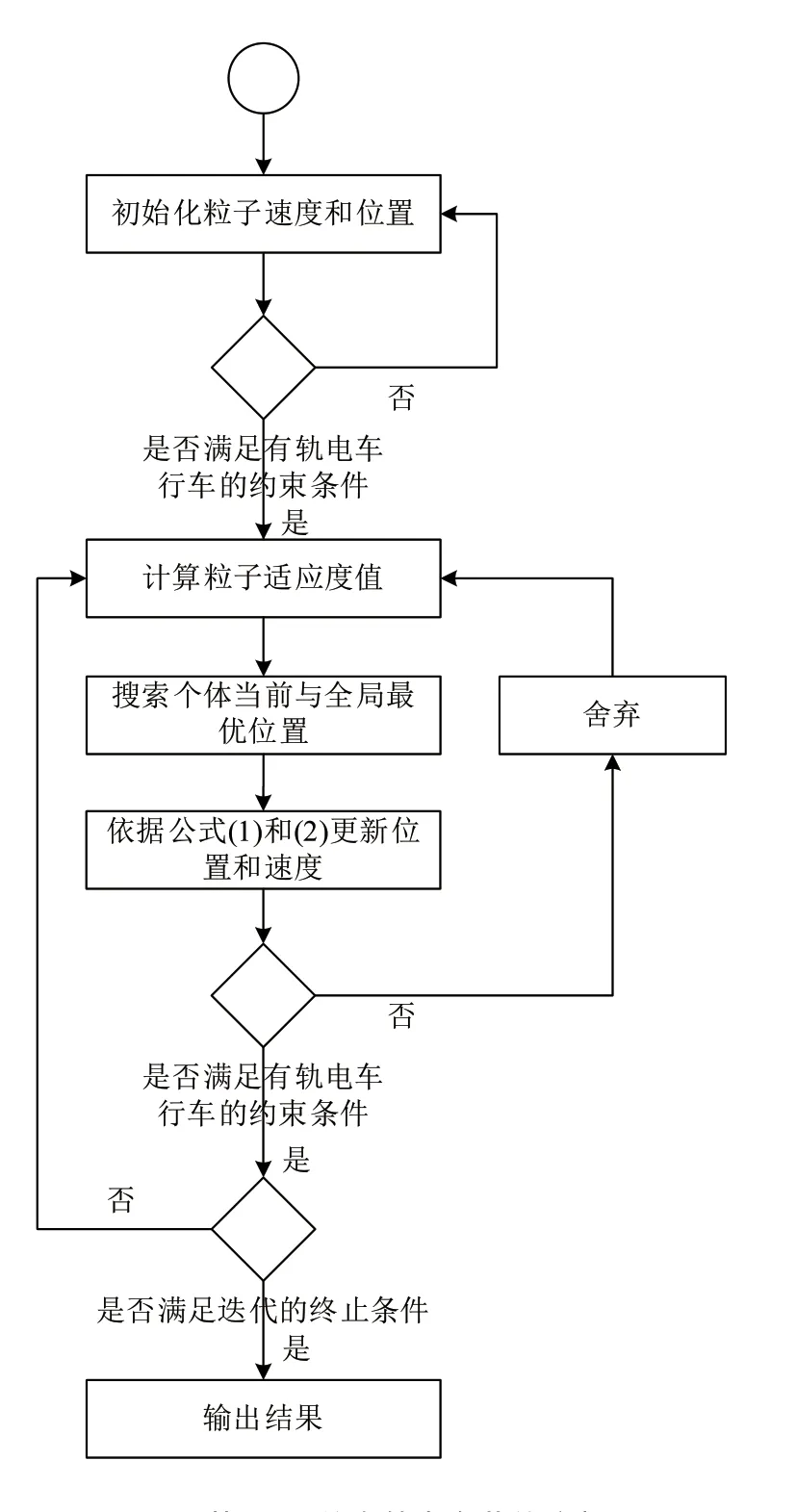
图4 基于PSO的有轨电车节能流程图

5 实验分析

本节采用Python语言，VSCode开发环境进行实验。选取某城市某有轨电车线路进行实验，PSO算法的参数和有轨电车运行场景参数如表1所示。

表1 实验参数设置

实验分别采用10、15和20个粒子，分别迭代50、50和70次，优化后的能耗分别为727583228.20 J、698163437.90 J 和664449800.41 J，实验结果如表2所示。

表2 实验结果

第3次实验的能耗和迭代次数如图5所示。实验开始时，粒子群优化算法的操纵策略花费能耗738023840.70 J，迭代进行到第30次时，能耗逐步稳定到664449800.41 J，其对应的操纵策略：v1为18.78 m/s，v2为10.41 m/s，S2为350.25 m，运行时间为 76.97 s。

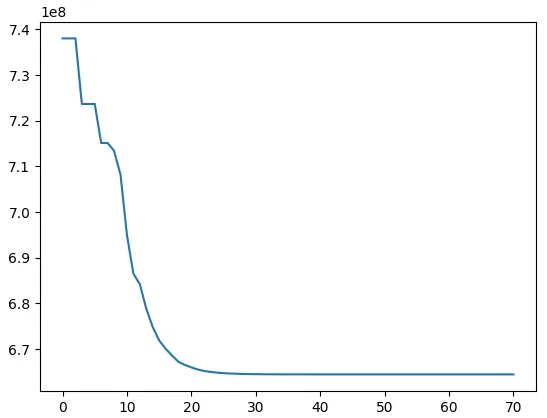
图5 能耗和迭代次数关系图

选取该有轨电车公司同一司机进行多次驾驶，和不同司机分别进行驾驶，将司机实际的操纵策略和本文算法的结果进行对比，结果表明本文算法优化的操纵策略能够节省15%~28%的能耗。

6 结束语

本文从操纵策略的角度提出有轨电车节能优化问题；然后，分析有轨电车在站间运行时的操纵策略，研究不同操纵策略对有轨电车节能优化的影响；然后，引入粒子群优化算法，结合有轨电车的2次巡航的经典运行模型，建立有轨电车粒子群优化算法的在建立新能源有轨电车电气传动模型和运动学模型的基础上，对自动驾驶下列车运行过程进行了节能研究，引入粒子群优化算法，提出了一种多目标有轨电车节能优化算法，通过与实际线路运行结果进行对比，证明了该算法的有效性和收敛性，优化了有轨电车的节能操纵策略，具有一定的工程意义，可供相关案例作为参考。