江汉平原过渡带黏性层状土弥散试验与模拟研究
2023-01-30刘泳佚史婷婷刘添文刘亚磊李梦茹
刘泳佚,史婷婷,王 清,刘添文,刘亚磊,李梦茹
(1.中国地质大学湖北巴东地质灾害国家野外科学观测研究站,湖北 武汉 430074;2.教育部长江三峡库区地质灾害研究中心,湖北 武汉 430074;3.中国地质调查局武汉地质调查中心,湖北 武汉430205;4.中国地质大学(武汉)环境学院,湖北 武汉 430074)
近年来,地下水环境质量问题愈发受到重视,地下水水分、溶质迁移规律的研究作为地下水环境质量问题的基础因而具有十分重要的意义[1]。地下水溶质运移本质是不同浓度溶液的混合置换作用,弥散系数与弥散度是控制溶质运移过程的重要参数,会直接影响水盐运移模拟计算的精确性和准确性[2−5]。现阶段,主要通过室内土柱试验和野外场地示踪试验获取弥散系数,室内土柱试验主要指一维弥散试验,即通过获得示踪溶质纵向穿透曲线从而求取纵向弥散系数。
自然环境中的土体大多成层分布,众多学者研究发现层状土因其粒径组成[6]、排列顺序[7−8]、土体厚度[9]等因素的影响,水分运移规律十分复杂,而水分作为溶质的载体对其影响巨大,因此层状土对溶质运移影响的研究显得十分必要。赵小二等[10]研究了流量条件对岩溶管道中溶质运移的影响,发现流量增大会使穿透曲线峰值浓度增大,拖尾缩短。郭蕾蕾等[11]开展室内土柱试验,发现黏土含量较高的壤土夹层对Br−穿透曲线有明显影响。Selim等[12]和Sharma等[13]均对Cl−在层状土柱中的穿透曲线进行研究,发现层状土的排列顺序对非饱和带水盐迁移影响尤其剧烈,而对于饱和带影响则相对较小。卜新峰等[14]通过室内和野外试验结果对比研究了弥散系数的空间尺度效应,认为室内试验所得参数不可直接用于场地,但是可以用于数值模拟迭代获取场地弥散规律。溶质运移研究中数值模拟的应用也十分广泛,邰托娅等[15]通过HYDRUS-1D建立了一维土柱溶质运移模型,模拟结果比较理想。葛建等[16]利用HYDRUS-1D软件对分层土柱进行模拟分析,发现上覆细粒会影响土壤持水能力。马蒙蒙等[17]通过HYDRUS-1D模型分析,发现饱和导水率和弥散度的差异使得入渗率有所不同,进而使Br−的穿透曲线差异明显。但是,目前层状土溶质运移试验研究多基于砂土、壤土为研究对象,黏性土中水盐运移缓慢同时受吸附影响较大但相关研究较少,同时试验土体多为人为设置土壤质地与容重,对于实际场地原状层土还原度不高。
基于此,本文以江汉平原——大别山区过渡带三水转换1#试验场为研究区,根据实际土层排列顺序、厚度比例采取钻孔原状黏性土等容重填充土柱,选取保守性阴离子Br−[18]进行系列穿透试验获取穿透曲线,并在等温吸附试验获取相关参数的条件下,基于一维水动力弥散方程通过HYDRUS-1D软件构建考虑吸附作用的一维土柱模型,对穿透过程进行反演从而获取各土柱弥散度及弥散系数等黏性土中溶质运移的相关参数,以实测穿透曲线与模拟穿透曲线对比,获取决定系数,验证模拟结果的准确性,并系统的探讨了研究区内不同土壤类型、层状结构对溶质运移的影响。成果可为黏性土中污染物或水盐运移研究提供参考,同时对江汉平原过渡带地下水环境保护、水质治理也具有重要应用价值。
1 研究区概况
研究区位于湖北省孝感市肖港镇三水转换1#试验场,地处江汉平原——大别山区过渡带澴水的二级阶地上,属亚热带季风气候,雨热同期,多年平均年降雨量1 112 mm。区内主要出露地层为第四系上更新统地层,下伏为古近系云台观组(Ey)基岩, 其中第四系上更新统二元结构明显,上部为厚层低渗黏性土层,下部为细粒砂质土层、砂砾石层,地下水主要赋存于下部砂砾石层中(图1)。已有研究表明,区内的上覆低渗黏土层和骤变的地层结构会对降水入渗和含水层补给产生巨大的影响,Liu等[19]通过试验场原位动态监测数据分析了不同深度层位黏性土中水分对大气降水和微承压地下水的动态响应关系,并总结了土壤水分运移的不同分带特征,其水盐运移规律可在此基础上进一步研究[20−22]。
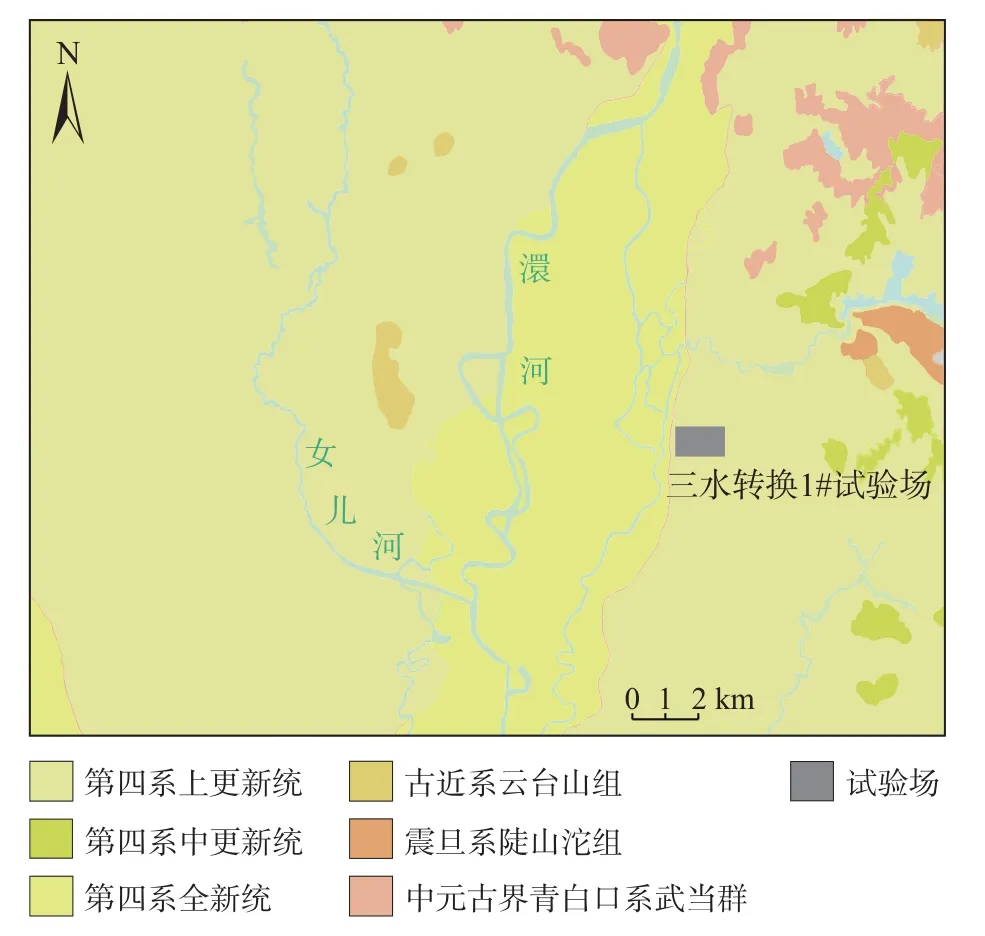
图1 研究区地质平面图Fig.1 Geologic ichnography of the study area
2 材料与方法
2.1 土样采集与测定
以前期试验场区钻孔揭露的地质结构分层为依据,结合不同层位土壤质地分类[23]及砂粒(粒径0.05~2 mm)、粉粒(粒径 0.005~0.05 mm)、黏粒(粒径<0.005 mm)含量,选择垂向5个深度钻孔原状土样进行试验,深度分别为2.0 m(粉质亚黏土)、5.0 m(粉质黏土)、6.5 m(粉质亚黏土)、13.5 m(砂质亚黏土)、14.2 m(砂质亚黏土)。供试土样于试验室用削土刀削成片状,放置于干燥通风处进行风干,研磨过筛(孔径2 mm)放入自封袋备用。供试土壤基本理化性质见表1。
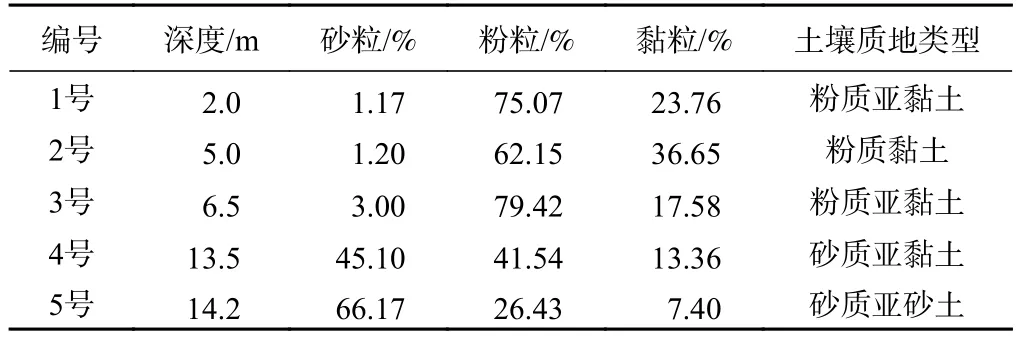
表1 研究区土壤颗粒分级数据Table 1 Soil particle classification data in the study area
2.2 等温吸附试验
对5个深度的供试土壤,各取8个50 ml的PET取样瓶,编号从0号到7号,按照土水比1∶5的比例分别称取5.0 g研磨后的风干土放入0——7号PET取样瓶。1——7号PET取样瓶中移入25.0 ml浓度分别为1,5,10,50,100,125,150 g/L的 NaBr溶液,0号 PET 取样瓶中移入25.0 ml去离子水作为空白对照组。置于恒温振荡器中振荡4 h后静置24 h备用。取10 ml静置后样品上清液,离心过滤(0.45 μm滤头),通过离子色谱仪(Metrohm 883 Basic IC plus型)对浸出液中的Br−浓度进行测量。
2.3 土柱穿透试验
土柱制备:根据试验场地土壤质地及地层结构共设计9个土柱(图2),其中1——5号是单层均匀土柱,材料分别为试验场垂向结构的5个深度土样(2.0,5.0,6.5,13.5,14.2 m);6——9号是按照实际场地地层排列顺序及地层之间厚度比,用上述5个深度土样填土的层状土柱,各土柱构型组成见表2。试验土样填充于内径4.0 cm,高为 14.8 cm的的塑料管中,管内侧进行磨砂处理,底部垫单层纱布,上铺 1.5 cm 厚的细沙,等容重填土后,土面铺1.0 cm的粗砂,管上部加盖用防水乳胶封死,盖壁接外径4 mm的长乳胶导管输送示踪溶液。

图2 土柱构型示意图Fig.2 Schematic diagram of soil column configuration

表2 试验各土柱具体构型Table 2 Specific configurations of soil columns in the experiment
试验过程:以定水头饱水入渗方式测定穿透曲线,先用去离子水使土柱自下而上完全饱水,稳定后计算各土柱的孔隙水流速,同时改用1号马氏瓶以2 m的固定水头在土柱上层通入浓度为 5 g/L 的 NaBr溶液(图3)。为保证1号马氏瓶液面稳定,通过2号马氏瓶对1号瓶以10 ml/h流速供液,超过固定液面的溶液通过溢流孔流入收集瓶后重复利用。在各土柱底部用 20 mlPET 瓶承接出流液,通过离子色谱仪(Metrohm 883 Basic IC plus型)测定不同时段内出流液中 Br−的质量浓度,从而得到穿透曲线。

图3 试验装置示意图Fig.3 Schematic diagram of experimental device
2.4 试验数据分析方法
(1)等温吸附模型
Br−等温吸附试验所得数据采用Freundlich吸附模型和Langmuir吸附模型进行拟合,模型表达式及参数如下[24]:
Freundlich 吸附模型方程:

Langmuir 吸附模型方程:
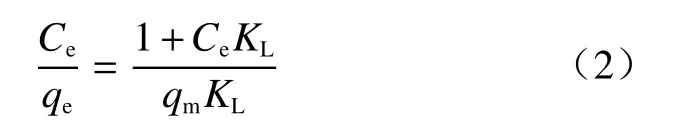
式中:Ce——溶液中 Br−平衡质量浓度/(mg·L−1);
qe——单位土体 Br−的平衡吸附量/(mg·g−1);
Kf——Freundlich 吸附常数/(L·mg−1);
n——非线性程度拟合参数/(L·mg−1);
qm——单位土体 Br−的最大吸附量/(mg·g−1);
KL——Langmuir 吸附常数。
(2)溶质运移模型
使用HYDRUS-1D 建立一维土柱溶质运移模型,定量模拟Br−随水分进入土柱后在吸附作用和不同土体构型的影响下在土柱中的迁移过程,从而反演出弥散度和弥散系数。模拟土柱均按实际填充情况设置参数,建立土壤水流模型设置上边界为定水头边界,下边界为自由排水边界。溶质运移过程考虑土壤对Br−吸附作用得到一维弥散方程[25]:
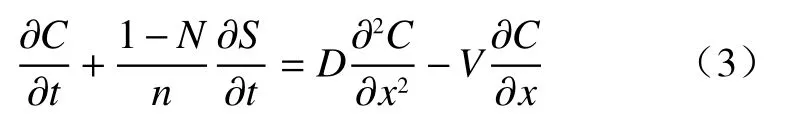
确定模型初始条件和边界条件:
初始条件:
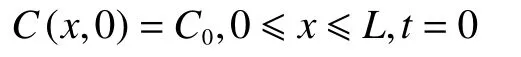
上边界条件:
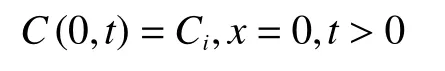
下边界条件:
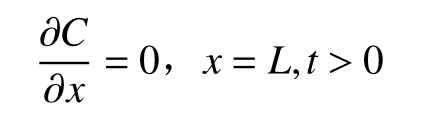
式中:D——弥散系数/(cm2·d−1);
S——单位土体 Br−吸附量/(g·L−1);
C——溶液中 Br−质量浓度/(g·L−1);
C0——土柱液相 Br−背景质量浓度/(g·L−1);
Ci——穿透溶液中 Br−质量浓度/(g·L−1),NaBr溶液质量浓度为5 g/L, Br−质量浓度为3.88 g/L;
N——土壤有效孔隙度;
V——土壤孔隙流速/(cm·d−1)。
HYDRUS-1D软件可以利用土壤颗分数据预测水力特征参数,将表1各层土颗分数据输入“Neural Network Prediction”系统,从而获得残余含水率、饱和含水率、进气值、饱和渗透系数和特定参数的取值[26]。模型中描述各类层状土吸附作用所需相关参数KL和Kf均由室内试验获得,各参数见表3,溶质穿透曲线及实测数据由一维土柱弥散试验提供,同时获取渗出液孔隙流速,从而可以对弥散参数进行反演。

表3 Freundlich方程和Langmuir方程拟合参数结果Table 3 Fitting parameter results of Freundlich equation and Langmuir equation
3 结果
3.1 不同分层土壤对Br−的等温吸附结果
采用Freundlich 吸附模型和 Langmuir 吸附模型对不同浓度条件下的吸附试验结果进行拟合。通过Freundlich模型和Langmuir模型的拟合曲线和拟合决定系数(R2),可以发现二者对Br−等温吸附结果的拟合效果均良好,Freundlich模型R2在0.921~0.986之间,而Langmuir等温模型R2在0.926~0.987之间,综合比较下Langmuir等温模型对土壤中Br−的吸附拟合效果较好。
3.2 一维土柱 Br−穿透曲线特征
穿透曲线是描述溶质在土壤运移过程中,渗出液相对浓度(C/C0)与相对应时间(t)的关系曲线,它可以直观的反映溶质在土壤介质运移过程中的浓度变化趋势[27]。试验中各土柱中Br−的穿透曲线如图4所示,对照各土柱具体构型(表2),可以看出各土柱渗出液中Br−的浓度在开始时均基本为0,在定水头的作用下,Br−的浓度开始变化同时曲线变陡,将此时定义为开始穿透时间,而后相对浓度逐渐增大到接近于1,曲线也随之变缓至基本水平,此时穿透结束,定义为完全穿透时间。

图4 试验各土柱溶质穿透曲线图Fig.4 Solute penetration curve of each soil column in the experiment
由图4(a)研究区各深度均质土柱穿透曲线可知,在其他条件均相同的情况下,穿透历时及完全穿透时间均表现为:2号>1号>3号>4号>5号,即5.0 m粉质黏土>2.0 m粉质亚黏土>6.5 m粉质亚黏土>13.5 m砂质亚黏土>14.2 m砂质亚砂土。各类型土中Br−的穿透历时相差很大,其中穿透最快的5号土柱穿透历时为1.14 d左右,而最慢的2号穿透历时为106 d左右。
3.3 弥散试验的模拟反演结果
本文通过HYDRUS-1D软件基于一维水动力弥散方程对土柱中Br−的弥散过程进行模拟反演从而求取弥散度及弥散系数,反演过程中通过实测穿透曲线与拟合曲线比较,获取R2验证模拟结果的准确性。各土柱穿透曲线模拟结果如图5所示,图中离散点为不同时间渗出液相对浓度的实测值。模型对弥散参数反演结果如表4和表5所示,可以看出模型拟合值与实测值R2均大于0.991,这说明模拟出的穿透曲线拟合程度较高,反演得到的弥散度(α)可信度较高,结合实测平均孔隙流速(V)可得到不同土体构型的弥散系数(D)。
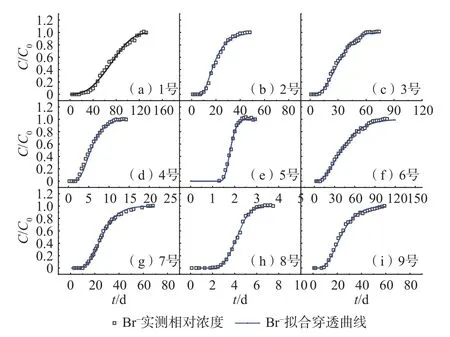
图5 各土柱穿透曲线拟合效果图Fig.5 Fitting effect diagram of penetration curve of each soil column

表4 均质土柱HYDRUS模型反演弥散参数Table 4 Dispersion parameters inversed by Hydrus model of homogeneous soil column
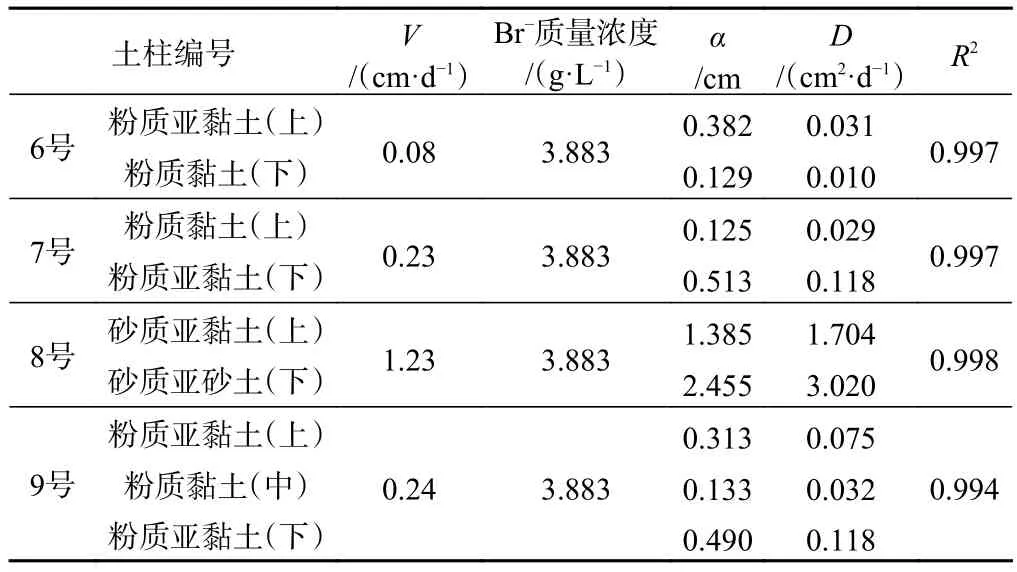
表5 层状土柱HYDRUS模型反演弥散参数Table 5 Dispersion parameters inversed by Hydrus model of layered soil column
4 讨论
4.1 黏性土对Br−的等温吸附分析
Langmuir吸附模型主要描述土壤颗粒表面单层活性吸附中心的吸附作用,土壤颗粒表面活性点位的数量影响着吸附量的大小,当活性吸附点位占满后,吸附量达到最大值[28]。试验中,Langmuir 等温吸附模型能较好描述土壤中Br−吸附过程,说明供试黏性土对Br−的吸附以弱的化学单分子层吸附为主,这也与黏土矿物吸附点位较多有关[29,30]。
通过表3对Langmuir等温吸附方程拟合结果中的qm分析,可以发现不同类型土壤对Br−的吸附量存在着明显差异,5.0 m粉质黏土饱和吸附量最大为10.169 mg/g,而13.5 m以下的砂质土则基本上小于粉质亚黏土,基本上呈现出粉质黏土>粉质亚黏土>砂质亚黏土>砂质亚砂土的特征,表明供试土壤对于Br−的吸附呈现出吸附量随黏粒含量增多而增大的趋势。
Freundlich 模型为经验模型,对多种吸附过程都有较好的适用性,可以很好的描述低浓度环境下的吸附作用[31]。Freundlich等温模型中1/n也称为吸附指数,是衡量吸附强弱的参数,一般情况下1/n的值在0~1左右,当1/n越小则表明吸附越容易发生,当1/n介于0.1~0.5时吸附易于进行[32]。试验中土壤对Br−吸附拟合的1/n值接近0.5,说明供试黏性土类矿物对Br−的吸附较易发生但吸附强度不高。
4.2 层状土中Br−穿透曲线特征分析
试验中随着土壤颗粒黏性的增大出流液流量减少,穿透历时及完全穿透时间延长,曲线斜率逐渐变小,这说明黏性土对Br−的穿透具有一定的阻碍作用。其原因是黏性细颗粒的增加使得土壤介质有效孔隙度变小,穿透路径变得曲折从而使渗透流速减小,同时也增加了含水介质中不动水区的体积,削弱了机械弥散对溶质的置换作用,这也佐证了虎胆·吐马尔白等[33]在砂壤土研究中提出的土壤渗透流速越大穿透到达峰值时间越短的观点,该规律同样适用于江汉平原过渡带黏性土。
图4(b)为亚黏土、黏土成层、两种均质土穿透曲线比较。图4(d)为粉质亚砂土、砂土成层、两种均质土穿透曲线的比较。可以发现将某种均质土中的一部分换为黏性较大、渗透性更差的第二种土后,土中Br−的穿透历时及达到峰值时间均会延后,但不会超过第二种土。这主要是因为土柱系统中细小的黏性颗粒增加,系统渗透性更差,同时不同类型土层交界面会形成水分横向流动对溶质迁移有一定的阻隔作用所导致[34]。图4(c)为均质亚黏土、上黏土下亚黏土、亚黏土夹黏土的穿透曲线图,7号和9号土柱中粉质黏土所占比例均参考研究区土层实际厚度比例接近1/10,与3号相比穿透曲线均出现了右移,这也是由于系统黏粒的增加和不同类型土层交界面对溶质迁移产生了阻碍导致,但二者穿透历程相差不大,这与同构型土柱在非饱和条件溶质运移过程中,上细下粗结构阻碍溶质迁移的规律有所矛盾[35]。其原因是本试验中土柱已充分饱水,并不会出现非饱和条件下水分先被上层细粒截流吸收的情况,由此可以认为,在饱和条件下层状土中溶质运移过程主要取决于含水介质中黏性颗粒的占比。
4.3 模拟反演参数分析
对比1~5号均质土柱(表4),弥散度在不同类型土壤中总体呈现出砂质亚砂土>砂质亚黏土>粉质亚黏土>粉质黏土的规律,随着土壤黏粒含量的增多,土壤平均粒径减小,弥散度同样呈减小趋势,这在一定程度上可以反映出孔隙介质的骨架特征。土壤孔隙流速与弥散系数均呈现出2号<1号<3号<4号<5号的规律,这是因为黏性土的增加使有效孔隙减少、水分溶质运移途径曲折所致,可以认为不同的土壤因其质地差异导致渗流速度不同从而影响弥散系数,土壤黏粒含量越高,渗流越差,弥散系数也越小。试验中5.0 m深度的粉质黏土弥散度为0.118 cm,而弥散系数仅为0.005 cm2/d,这也说明研究区内粉质黏土层的存在会很大程度的阻碍地下水的水分、溶质运移,上部含水层中的污染物或有机质很难穿透该层向下运移。
对比表5中HYDRUS模型反演出的4个层状土柱中各层土壤的弥散参数,并和与之相对应的均质土柱各参数比较,弥散系数变化幅度均大于弥散度变化幅度,如:6号,上层2.0 m深粉质亚黏土弥散度为0.382 cm,弥散系数为0.031 cm2/d,而与之对应的1号弥散度为0.327 cm,相差14.39%,弥散系数为0.048 cm2/d,相差54.84%。这说明了在试验的层状土柱中,因为运移距离较短,渗流速度较慢,弥散度空间尺度效应较小,变化幅度不大,但是因为层状结构的存在导致土柱平均孔隙流速变化剧烈,从而明显改变了弥散系数[36]。由此,结合上文对不同类型层状土穿透曲线的分析可以认为:在同一尺度下,对于层状土无论其土壤组成类型还是层厚及排序,其本质都是改变了土柱平均孔隙流速从而影响弥散作用,平均孔隙流速越小其弥散系数越小。
综上,通过各参数对江汉平原过渡带试验场地纵向弥散规律进行整体分析,此次反演结果表明:研究区内0.2~4.4 m及5.7~12.5 m亚黏土弥散度范围为0.327~0.481 cm,4.4~5.7 m粉质黏土弥散度约为0.118 cm,13.0~15.0 m砂土弥散度范围在1.200~2.561 cm,反演结果与李培月等[37]和司高华等[38]对砂土、黏土弥散度的室内研究结果相似。同时,由室内试验得出,研究区内0.2~12.5 m上覆黏性土渗透系数小(10−6cm/s数量级),且弥散系数为0.005~0.048 cm2/d,远小于下部13.0~14.0 m砂土含水层弥散系数0.524~7.477 cm2/d,差值达到了至少两个数量级,这进一步说明了研究区0.2~12.5 m上覆厚层亚黏土夹黏土结构对区域垂向渗流及弥散具有主要控制作用,也说明江汉平原过渡带厚层黏土的存在会较大程度上阻碍了土壤水分、溶质的运移。在黏土垫层隔污防渗的实际研究中,学者们发现厚度大于2 m,饱和渗透系数在10−7cm/s数量级左右的黏土衬层对渗滤液有明显的阻隔作用[39−40]。这也从实际应用层面定性说明研究区上部含水层具有良好的截污性能,后期依据本文所得各项参数,结合研究区实际边界条件开展数值计算,可以定量表征水盐及污染物在江汉平原过渡带土体中的具体运移过程。
5 结论
(1)采用 Freundlich 模型和 Langmuir 模型均能较好的拟合吸附试验结果,研究区不同类型土壤对Br−的饱和吸附量有所差异,基本上呈现出粉质黏土>粉质亚黏土>砂质亚黏土>砂质亚砂土的规律,随着土壤中黏粒比例的增大,表面活性点位增多,土壤对溶质吸附作用愈发明显。
(2)层状土中土壤质地与结构均会影响穿透曲线的形状。试验中研究区各深度均质土穿透历时及完全穿透时间均表现为:5.0 m粉质黏土>2.0 m粉质亚黏土>6.5 m粉质亚黏土>13.5 m砂质亚黏土>14.2 m砂质亚砂土,黏粒的增加会对溶质运移产生阻碍。对试验中层状非均质构型土柱与均质土柱比较,发现土柱系统渗透性和层状土交界面均会对弥散作用产生一定影响,但一维饱和土柱中的弥散过程主要取决于含水介质系统中黏性颗粒的占比。
(3)通过HYDRUS-1D软件构建模型反演弥散参数,R2均大于0.991,拟合效果较好。考虑吸附作用的影响,研究区内粉质黏土弥散系数为0.005~0.048 cm2/d,远远小于下部13.0~14.0 m砂土含水层弥散系数0.524~7.477 cm2/d。同时分析发现在同一尺度下,对于层状土无论其土壤组成类型还是层厚及排序的影响,其本质都是改变了土壤的平均孔隙流速从而影响弥散作用,平均孔隙流速越小其弥散系数越小。
