非支配排序遗传算法-Ⅱ组合赋权的水体富营养化多维联系云评价*

晏嘉辉 汪明武 陈光耀 金菊良

(合肥工业大学土木与水利工程学院,安徽 合肥 230009)

水体富营养化对人类健康和经济社会发展造成了巨大危害,如何准确有效地评价水体富营养化程度成为研究重点[1]。营养状态指数法[2]、支持向量机[3]、人工神经网络[4]、粗糙集理论[5]、模糊数学法[6]等水体富营养化评价方法相继提出,但上述方法仍然存在局限性[7-8],且仅考虑了指标的某一类不确定性,而实际富营养化评价指标涉及多重不确定性,还有分类边界的模糊性和转换情况、评价指标的区间性。近期出现的正态云模型为综合描述随机性和模糊性提供了新思路,但其要求数据正态分布,忽视了评价指标的有限区间分布状态,并随着指标和样本数的增加而变得复杂。汪明武等[9]提出了联系云模型来克服正态云的缺陷,但联系云模型涉及指标权重[10]193,权重分配的合理性会影响到评价结果的可信度。为有效刻画有限区间内指标的模糊随机性和离散性,并协调不同权重的重要性,更合理确定权重,许多学者提出了多种权重优化方法。YU等[11]依据混合多属性决策理论提出了一种基于指标重要性的组合权重方法;任春华等[12]基于权重差异度最小化原理设计了一种三段式的公平权重算法;DUMAN等[13]通过优劣解距离算法组合主客观权重;石莉等[14]提出了一种基于粒子群优化算法的权值聚合方法。但这些方法没有充分考虑不同权重耦合所造成的诸多不确定性因素对最终组合权重的影响。为此,本研究采用非支配排序遗传算法-Ⅱ解决权重系数确定问题,并将获得的最优组合权重与多维联系云相耦合,探讨一种新的水体富营养化评价模型,实现有效刻画有限区间内的模糊随机性和离散性,使富营养化评价结果更合理和更可靠。

1 理 论

1.1 多维联系云模型

联系云是耦合正态云模型[15]和联系数理论发展起来的,现已用于诸多不确定性问题的分析,针对水质评价问题可定义如下：设水体富营养化共有n个等级、m个评价指标,则隶属于分类标准某个等级的概率可通过云滴数为h的m维联系云来表示。水质数据集P是一个m维的定量论域,等级集合Q是P的一个定性概念。如果P中所有元素均为概念Q的随机事件,并且满足：P中的元素x(又称为云滴)服从数学期望为Ex、均方差为En’的正态分布,而En’又服从数学期望为En、均方差为He的正态分布,那么P中所有元素的分布称为多维联系云。

联系云模型能精确描述各指标样本数据和分级标准之间的不确定性关系,为水体富营养化实际状况和分级转换态势的有效刻画提供了新的途径。同时,联系云没有限制指标分布状况,可使计算过程更客观可靠,贴近实际状况,具有更强适应性。在案例研究中,一维联系云模型必须为每个分类指标单独设置多个云,而多维联系云只需为所有指标建立一个云,计算效率大大提高[16]。

1.2 基于非支配排序遗传算法-Ⅱ的组合赋权

以往研究表明,仅考虑指标的重要性或内在信息的单一权重可能会导致分类结果偏离实际情况[17],由主观和客观权重共同构成组合权重才能获得合理的评价结果。此外,主观权重由于专家知识水平、经验等方面的差异,客观权重受到样本数据误差、计算理念不同等方面的影响,两者均存在不确定性。当多个权重组合时,组合权重也具有不确定性。组合系数是不确定性的一种表达形式,且具有两类目标函数。本研究基于非支配排序遗传算法-Ⅱ确定最优组合系数,并据此获得最终组合权重。

非支配排序遗传算法-Ⅱ组合赋权法将多种主、客观赋权法有机结合,综合了多型权重各自的优势。权重约束优化模型客观描述了权重计算过程中的多重随机不确定性,对每种权重各自计算过程和权重组合带来的不确定性进行了量化。用非支配排序遗传算法-Ⅱ直接求解多目标权重模型,避免转化为单目标模型,既简化了计算过程又降低了潜在的不确定性,可在一次运行中得到一组满足精度要求的解集(折中解),最终结果从中筛选出一个最优值。解的情况更符合实际,因为组合系数是权变量的概率函数,具有一定的波动性。引入精英保留、密度值估计和快速非支配排序等策略,减少了共享半径等参数,计算复杂度的阶数降低了g次(g为初始种群个数),大大提升了种群的整体进化水平。

1.3 非支配排序遗传算法-Ⅱ组合赋权的多维联系云模型

富营养化评价涉及多种因素,根据多个指标对水体进行分级的过程充满了不确定性、非线性和模糊性。仅根据联系云计算联系度,没有考虑指标本身属性对等级划分的影响。为保证富营养化分级的准确性,采用非支配排序遗传算法-Ⅱ组合赋权法合理确定指标权重,并将权重向量的分量与水质每一等级联系度中的各指标分量相耦合,得到新的联系度。

新的联系度计算中每一指标分量既囊括指标权重,又包含联系云特征值,以及由特征值随机产生的“云滴”,对全部指标的所有模糊信息都进行了量化。定义的联系度计算公式相对简单有效,最大程度上消除了定量数据与定性分级转化过程中的不确定性。定量的实测水富营养化数据经过非支配排序遗传算法-Ⅱ组合赋权的多维联系云模型转化,实现定性等级的精确划分。

2 评价方法

2.1 基本流程

非支配排序遗传算法-Ⅱ组合赋权的水体富营养化多维联系云评价的基本流程如图1所示。

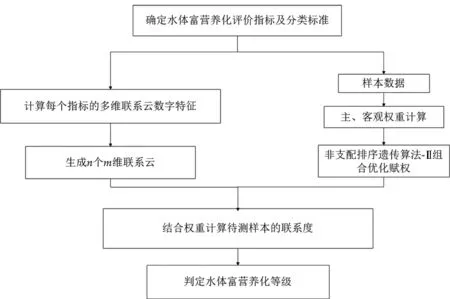
图1 基本流程Fig.1 Basic process

2.2 具体步骤

2.2.1 确定评价指标和分类标准

富营养化发生机制复杂,影响因素众多,参考文献[18]和《地表水环境质量标准》(GB 3838—2002),选取5类评价指标(叶绿素a(Chl-a)、总磷(TP)、总氮(TN)、高锰酸盐指数(PI)和透明度(SD)),将水体富营养化划分为6个等级(见表1[10]195)。

2.2.2 确定权重

应用组合权重来统筹多种主、客观赋权法的优势,客观赋权法采用主成分分析法和熵权法,主观权重通过层次分析法确定。同时,为更客观反映指标实际信息,采用改进的CRITIC法[19]对客观权重作进一步补充。

根据Shannon信息熵[20]的概念和权值相对差异性的衡量标准,分别建立第一类不确定性目标函数(f1(α)，见式(1))和第二类权重一致性目标函数(f2(α),见式(2))。结合约束条件,即可建立指标权重的多目标优化模型(见式(3))。采用非支配排序遗传算法-Ⅱ对权重模型进行求解,以确定最优组合系数,并据此获得最终权重(见式(4))。

(1)

(2)

(3)

(4)

式中：α为组合系数向量;k是赋权方法序号;l为赋权方法总个数;αk为第k类赋权方法所确定的权重的组合系数;j为评价指标序号;Wj为第j个评价指标的最终权重;wkj为第k类赋权方法所确定的第j个评价指标的权重;F(α)为总体目标函数;W为组合权重向量;wk为通过第k类赋权方法计算得到的权重向量。

2.2.3 建立多维联系云模型并计算联系度

设水体富营养化评价中共有m个评价指标,计算m维联系云的数字特征值并确定云滴数h,在有限区间内生成m维联系云的h个云滴。基于样本实测数据,结合评价指标权重,计算富营养化隶属于某个级别的联系度。具体的联系度和参数计算方法为：

(5)

(6)

2.2.4 水体的整体富营养分级

联系度其实就是水体的整体富营养化隶属于每个等级的概率。整体富营养等级取n个联系度中最大值。

3 案例研究

3.1 数据来源

采用24个湖库的水质数据进行富营养化程度评估,数据来源于金相灿等[22]对我国水体富营养化情况的调查资料。本研究目的在于提出一种适用于不同流域分布、地质状况和营养条件湖库的通用富营养化评价模型,这24个湖库的地域、地形和营养条件具有很强的代表性,使用这些湖库的数据便于检验本研究模型对不同地域类型湖库的适用性。这些数据是实地采集水样检测后多方汇总得到的,检测方法合理且符合相应规范要求,具有较高的可靠性,其中包含了本研究评价体系中的所有评价指标,契合度很高。选取的实例数据多次被用于验证国内新的富营养化评价模型(如改进模糊综合评价、博弈论-联系云等),便于将本研究模型的评价结果跟其他方法的结论进行比较分析,从而验证本研究的准确性。

表1 水体富营养化等级划分标准Table 1 Classification standards of water eutrophication

3.2 案例评价

利用种群数为100的非支配排序遗传算法-Ⅱ对4种权重进行组合(见表2)。在各等级下生成2 500个云滴以模拟不同等级的多维联系云。为便于可视化理解,以Chl-a和PI分别构建一维联系云(见图2)。最终的评价结果及对比见表3。

由表3可见,本研究模型评价结果与其他方法基本一致,其中高州水库、蘑菇湖和固城湖的等级存在一定争议;博斯腾湖、淀山湖、于桥水库、南四湖、西湖的评价结果与b～f完全一致,只与a相差一个等级。a～f评价高州水库的结论中各有3个Ⅲ、Ⅳ级,显示高州水库的富营养状况介于Ⅲ、Ⅳ级之间,具体分级存在模糊性;本研究模型计算其水样的Ⅲ、Ⅳ级联系度分别为0.210 8、0.143 1,其余等级联系度数值都很小,故评价为Ⅲ级,同时表明高州水库的富营养化模糊程度——虽然属于Ⅲ级,但也存在倾向Ⅳ级的趋势。查看数据发现,该样本5个评价指标实测值中,属于Ⅱ级的有1个(Chl-a),属于Ⅲ级的有2个(PI、SD),属于Ⅳ级的有2个(TP、TN),且TN浓度虽然属于Ⅳ级却非常接近Ⅲ级的上限,所以本研究模型Ⅲ级的评价结果更准确,而a、c和f的Ⅳ级评价与实际存在偏差。蘑菇湖水样的5个评价指标中,属于Ⅴ级的有2个(Chl-a、SD),属于Ⅵ级的有3个(TP、TN、PI),但是Chl-a是公认的最重要的水体富营养化评判标准[23],且TP、TN、PI十分接近Ⅴ级的边界值,所以a、b、c和e判定为Ⅵ级是不恰当的,本研究模型的Ⅴ级更合理。同样基于联系云模型,本研究模型比其他方法评价结果更合理准确,表明非支配排序遗传算法-Ⅱ组合赋权法要优于对比方法的单一主观或客观赋权法以及博弈论这一传统数学规划赋权法。

同理可知,本研究固城湖的富营养化评级Ⅴ也是准确的。该案例中,包含100种群个体的非支配排序遗传算法-Ⅱ的算法复杂度阶数是传统非支配排序遗传算法的1/100,五维联系云的计算时间只有一维联系云的1/5。

案例中湖泊水库的富营养化等级均在Ⅲ级及以上,评价结果为Ⅴ级的湖库最多,数量为10个,占总共24个湖库的41.67%;其次是Ⅵ、Ⅳ级的湖库,数目分别为8、4个,分别占总数的33.33%、16.67%;水体富营养化Ⅲ级的湖库最少,只有2个,占比8.33%。这反映了在采样年份24个湖库营养程度普遍较高的现实,比照相关调查资料可知,基本符合当时的实际富营养化状况。如滇池草湖,水体叶绿素浓度严重超标,水面藻类覆盖面积很大,水质恶劣,其富营养化程度远较滇池外海严重,故将其富营养化等级定为最高的Ⅵ级是正确的。针对等级相同的情况,本研究模型可对水质状况作更精确细致的区分。如洱海和高州水库同为Ⅲ级,但比较两者的联系度可发现,洱海的数值明显更大,说明洱海的富营养状况更严重。高州水库Ⅲ、Ⅳ级联系度较接近,相邻两等级的差值约为洱海的5倍,可认为高州水库水质变化的概率要远大于洱海,洱海水质的稳定性更高。

表2 组合权重和组合系数Table 2 Combination weight and combination coefficient

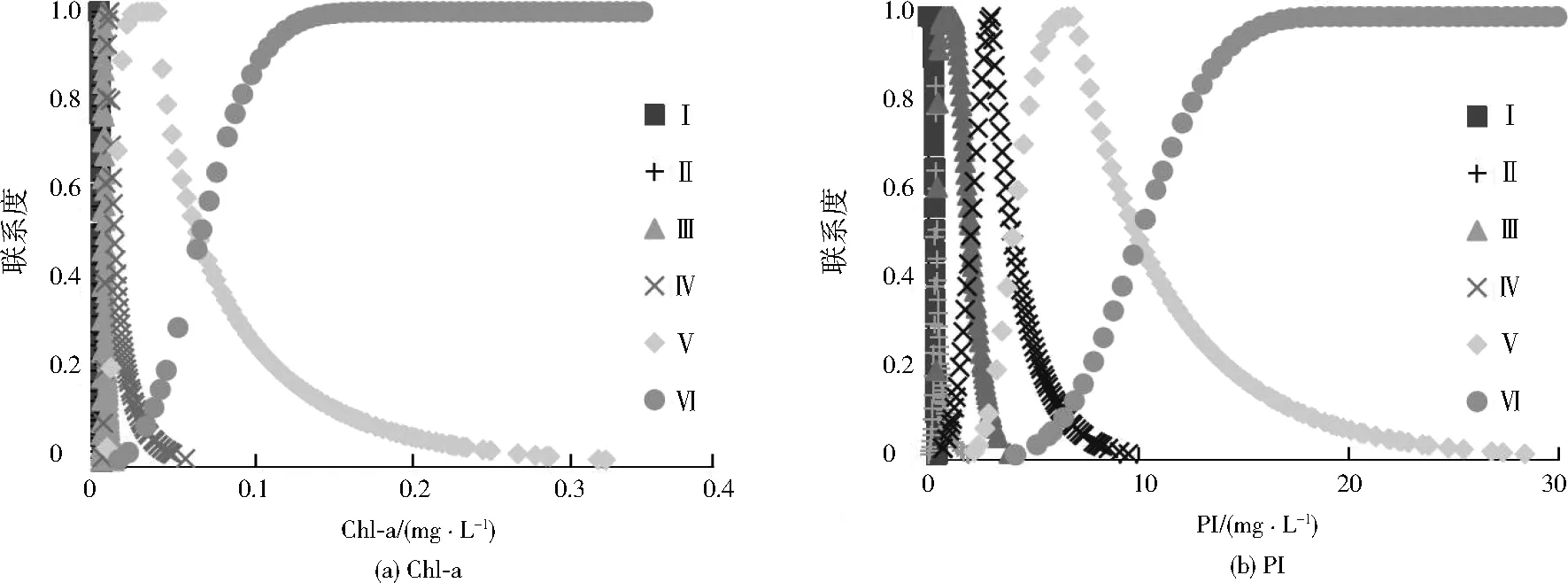
图2 Chl-a和PI的一维联系云Fig.2 One-dimensional connection cloud for chlorophyll a and permanganate index

表3 评价结果及对比1)Table 3 Result and comparison of evaluation

4 结 论

(1) 非支配排序遗传算法-Ⅱ组合赋权法量化了不同赋权法所得权重的随机性及其与真实权重的一致性等多重模糊特征,综合了多种主、客观权重理念的优势,保持赋权结果准确性的同时又降低了计算复杂度的阶数。

(2) 联系云模型实现了对有限区间内的非对称指标标准的刻画,在实际的多种水体评价中展现出更强的适应性。从一维扩展到多维,可大大缩短计算时间,提高了大样本实例的处理效率。结果准确合理、符合实际,定量表征了富营养化等级与指标间的多重随机性和模糊性,既精确评价了水质状况,又指示了水质变化的趋势。

(3) 案例中24个湖泊水库的富营养化等级均在Ⅲ级及其以上,评价结果为Ⅴ级的湖库数量最多,为10个,占总数的41.67%;其次为Ⅵ、Ⅳ级,分别占33.33%、16.67%;数量最少的是Ⅲ级湖库,只占8.33%。所得结论跟实际富营养化状况基本一致,表明本研究方法应用于评价富营养化等级是有效可行的,为解决水体富营养化评价及类似问题提供了新的参考。