压电悬臂梁振动控制系统联合仿真与实验研究

李康敏，张 柯，刘永斌，琚 斌

(安徽大学 电气工程与自动化学院，安徽 合肥 230601)

0 引言

现代工程和机械操作时存在的不必要结构振动会加速机器的疲劳损伤，影响机器的正常工作。1982年，美国航天局发射陆地探测卫星挑战者号执行探测任务时，由于探测仪旋转部分受到驱动系统的振动干扰，影响了探测仪拍摄的图像质量，导致传输处的图片某些部分模糊不清，从而阻碍航天任务的进一步探索。1992年，阿姆斯特丹空难，由于发动机架的销钉常年受到驱动系统各频率的振动，使得销钉疲劳断裂造成重大事故。因此，研究机械结构的振动控制对于提升其工作状况和使用寿命具有重要的研究意义和价值。

在早期的结构振动控制中，根据能量的消耗方式，结构振动控制可分为主动控制、被动控制及半主动控制。被动控制拥有不需要外界能量即能实现机械结构振动控制的优点，结构简单且易实现，但需要通过电路的设计来耗散、吸收结构的能量，抑制结构振动的效果有限。1979年，Forward[1]首次提出利用压电智能材料和电感组成分流电路进行实验，以能量耗散的方式实现悬臂梁结构的振动控制，验证了电路分流消耗能量的实验可行性。吴巧云等[2]基于能量最小原理，推导了两种被动阻尼器优化参数的解析表达式，并通过二自由度和多自由度系统的数值算例验证了优化系数的阻尼器对结构控制的有效性。半主动控制可应对更复杂的环境，但不能将已有主动控制算法直接应用于半主动控制中，灵活性比主动控制弱。Takamoto Ikuya等[3]提出基于分段恒定输入的预测开关(PSPCI)方法可预测半主动控制输入，并使控制输入的确定多样化，从而有效地抑制结构的振动。Riascos Carlos等[4]提出了一种半主动控制策略的加压调谐液柱阻尼器 (PTLCD) 在正面看台型钢结构上的实验。实施主动控制需要额外的能量实现控制，Fanson等[5]提出使用正反馈位置的方法实现悬臂结构的振动控制，针对大型结构的复杂性和多模态，利用多个压电致动器和传感器实现了结构的多模态振动控制。Rogacheva Nelly[6]提出使用基于数学的模型来解决结构的主动振动系统。隋大鹏等[7]和刘涛等[8]应用哈密顿原理的数学方法建立了柔性梁动力学模型，并在Simulink中进行仿真研究。近期利用智能算法进行识别并建立结构系统模型的研究逐渐增多。宋哲等[9]利用神经网络算法对悬臂梁进行系统识别，并且利用该算法实现悬臂梁的主动振动控制。李辉等[10]基于改进的一阶剪切变形理论、能量法和瑞利-里兹方法,推导结构系统自由与强迫振动方程建立系统模型。

目前传统的机械结构振动控制需要建立数学模型进行解析，但考虑到建立数学模型的复杂性及系统模型精确性不高的问题，本文应用COMSOL仿真软件搭建悬臂梁系统有限元模型，并结合控制器算法模型进行联合仿真，提高了系统模型的精度，增加了系统设计的灵活性。

由于主动振动控制在低频振动控制领域拥有更好的控制效率，本文采用压电材料作为主动控制驱动器，并应用比例、积分、微分(PID)控制算法在悬臂梁一阶固有频率下进行振动抑制研究。传统PID控制参数的整定一般需根据经验手动调试，根据误差进行凑试，但实际情况中会出现最优化困难，耗费精力且不利于实时反馈等问题，因此，本文利用遗传算法来优化PID控制器的参数。压电悬臂梁振动控制的联合仿真与实验结果均表明，利用遗传算法优化PID参数的方法是有效的，并且该算法模型具有很好的鲁棒性，在悬臂梁不同驱动位置处均可获得最佳的PID整定参数，实现振动抑制最佳效果。

1 建立联合仿真模型

为了避免建立悬臂梁数学解析模型的复杂性，本文首先需要在多物理场仿真软件中建立压电悬臂梁的有限元模型。图1为COMSOL上搭建的悬臂梁系统简要模型。为了使模型更符合实际情况，本文引入点载荷输入变量用于模拟外界干扰。此外，为了直观观测悬臂梁的振动变化过程，可在悬臂梁末端设置位移变量，实时监测悬臂梁振动位移。为形成闭环反馈系统，在本文设计执行器输入变量与传感器输出信号。搭建好压电悬臂梁模型后，需要先进行特征频率研究，分析其固有频率、振型和应力分布。根据仿真好的特征频率结果和应力分布结果，后期可优化压电陶瓷片的粘贴位置，为后续的实验提供理论和指导作用。

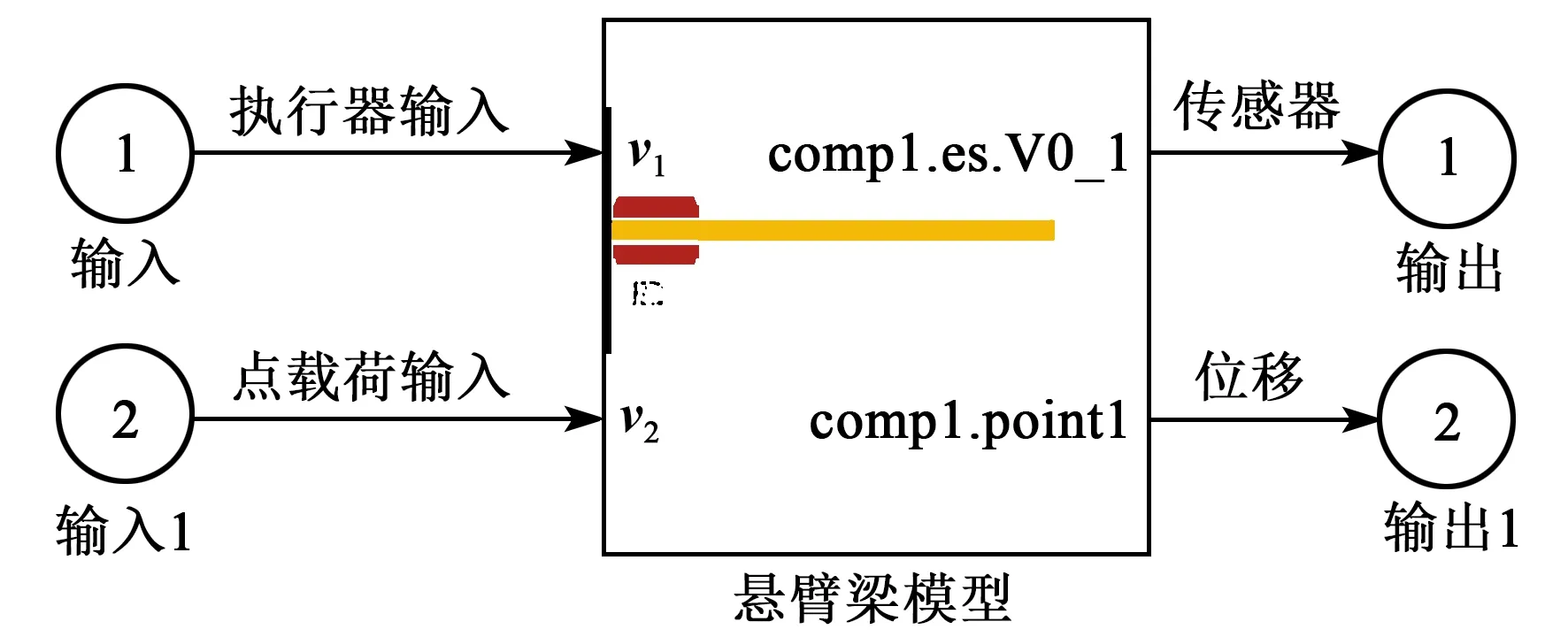
图1 COMSOL中悬臂梁系统模型

表1为悬臂梁与压电陶瓷的材料参数。需要给模型添加仿真环境及初始条件，添加固体力学和静电的耦合物理场，并设置好悬臂梁和压电陶瓷片的初始值，在悬臂梁根部施加固定约束，在自由端添加垂直于悬臂梁的一阶共振频率正弦激励信号，模拟外界干扰。考虑实际压电陶瓷具有阻尼，对压电材料添加一定的瑞利阻尼，其质量阻尼参数和刚度阻尼参数设置如表2所示。

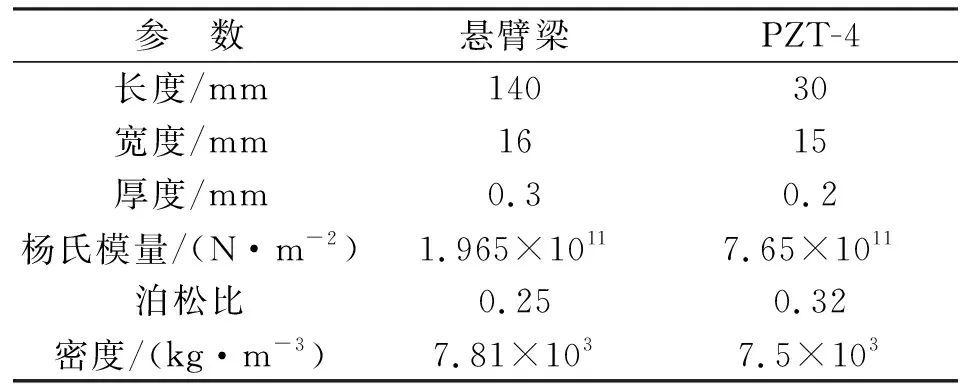
表1 悬臂梁和压电陶瓷片(PZT-4)材料参数

表2 瑞利阻尼参数

图2为通过特征频率分析所得悬臂梁的一阶振型。图中，悬臂梁的中轴线上布置30个探测点，依次从根部至端部，在端部施加一阶共振频率载荷为50 mN，得到应力分布如图3所示。由图可看出，悬臂梁位于根部的应力最大，从根部至尾部应力逐渐减小。根据力学知识可知，压电陶瓷片位于悬臂梁根部可有效地进行信号感应和振动抑制。将压电陶瓷片粘贴在位于应力最大处的根部上下面，再次对压电悬臂梁进行特征频率下的仿真分析，求出结构模型系统一阶共振频率f=22.69 Hz。

图2 悬臂梁一阶振型

图3 一阶模态悬臂梁应力分布

图4为本文所设计的压电悬臂梁联合仿真模型，其中灰色区域为压电悬臂梁结构。图中，Kp、Ki、Kd分别为比例参数、积分时间常数、微分时间常数。悬臂梁主体使用的是锰钢材料，其上下表面贴有2片压电陶瓷，分别作为感应器(PZT2)和执行器(PZT1)。压电陶瓷具有正-逆压电效应，当处于正压电效应时，可作为感应器；当处于逆压电效应时，可作为执行器。给悬臂梁点载荷一个正弦力信号，激励起压电悬臂梁的一阶振型。位于悬臂梁根部下方的压电陶瓷片PZT2感应到应力变化，充当感应器，其产生相应的电信号经过控制器计算处理反馈于PZT1上，抑制悬臂梁的振动。将COMSOL软件建立的压电悬臂梁系统导入到Simulink中即可实现联合仿真。根据前面计算出的压电悬臂梁的一阶共振频率f，在Simulink中在点载荷上添加频率为f的正弦力信号，激励压电悬臂梁振动。在Simulink搭建遗传算法在线优化PID参数：先对振动时PZT2的感应信号进行采集，经过优化参数后的PID算法，对感应信号进行比例(Kp)、积分(Ki)、微分(Kd)，最后对3种信号求和，计算出控制电压，并反馈在PZT1上以抑制悬臂梁的振动。

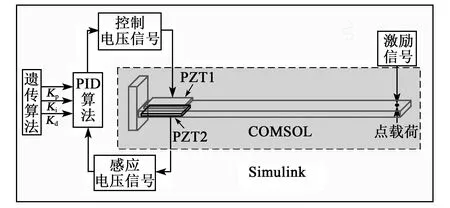
图4 压电悬臂梁系统振动控制联合仿真

2 振动控制器设计

2.1 PID算法

图5为PID控制器。PID算法具有可靠性高，算法简单易实现以及鲁棒性高的优点，已被广泛应用于各类工业控制[11-12]。PID控制思想是基于误差变量的比例、积分、微分线性组合，构成控制信号实现对被控对象的控制[13]。

图5 PID控制器

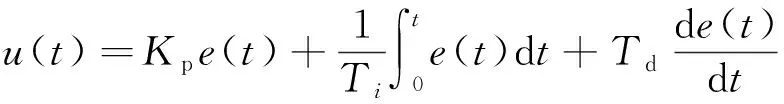
(1)

式中：e(t)为压电陶瓷感应信号和参考信号之差；u(t)为控制信号。

考虑实验的激励信号是动态持续的一阶共振频率信号，应用增量式PID算法提高系统响应速度和响应效果。增量式PID控制是利用本次控制量和上次控制量的差值进行PID控制的一种控制算法,即：

u(k)=u(k-1)+Δu(k)

(2)

式中Δu为增量控制，当前控制量为上一时间段的控制量加上增量。

图6为增量式PID算法在Simulink中的简单实现过程。与其他PID算法相比，增量式PID算法能记住上个时间段的控制量，并根据现时的误差值进行PID参数的线性累加[14-15]。

图6 增量式PID在Simulink中的实现

2.2 遗传算法

因为PID参数的取值会影响控制的效果，所以为了取得悬臂梁系统的最佳控制，需按照丰富的经验进行参数调整，但不能确保悬臂梁振动控制系统是否处于最佳状态，并且会花费大量的时间和精力。为了更好更快地整定PID参数，本文应用遗传算法整定PID参数；遗传算法模仿生物的自然进化机制和遗传机制，是一种过程量的寻优搜索，以寻找Kp、Ki、Kd的最佳值[16-18]：

1) 根据PID调试经验确定Kp、Ki、Kd的取值范围。本文中Kp寻优范围为[0,100]，Ki和Kd的寻优取值范围均为[0,5]。

2) 生成初始种群，并预分配空间内存，确定遗传算法的参数。种群规模Po=100，交叉概率Pc=0.6,染色体变异概率选择Pm=0.1，染色体长度，即种群参数最大值选择M=15，遗传代数(即迭代次数)Mi=100。

3) 确定目标函数J和适应度函数F。目标函数为

(3)

式中e(t)为悬臂梁的误差信号;u(t)为控制电压信号;ts为实际输出调整到期望输出的误差范围之内所需时间，即调节时间，w1,w2,w3分别为各自指标所占权值，本文所取值为[0.8,0.1,0.1]。适应度函数取：

(4)

图7为遗传算法优化PID参数流程。确定好各参数和适应度函数之后，在Simulink上搭建仿真图，如图8、9所示。在仿真开始前，需要先进行离线训练，通过优化得到最佳PID参数,并将其用于Simulink的联合仿真。根据位于根部致动器粘贴位置，在线整定PID参数，图10为PID参数优化过程。图11为适应度优化曲线。

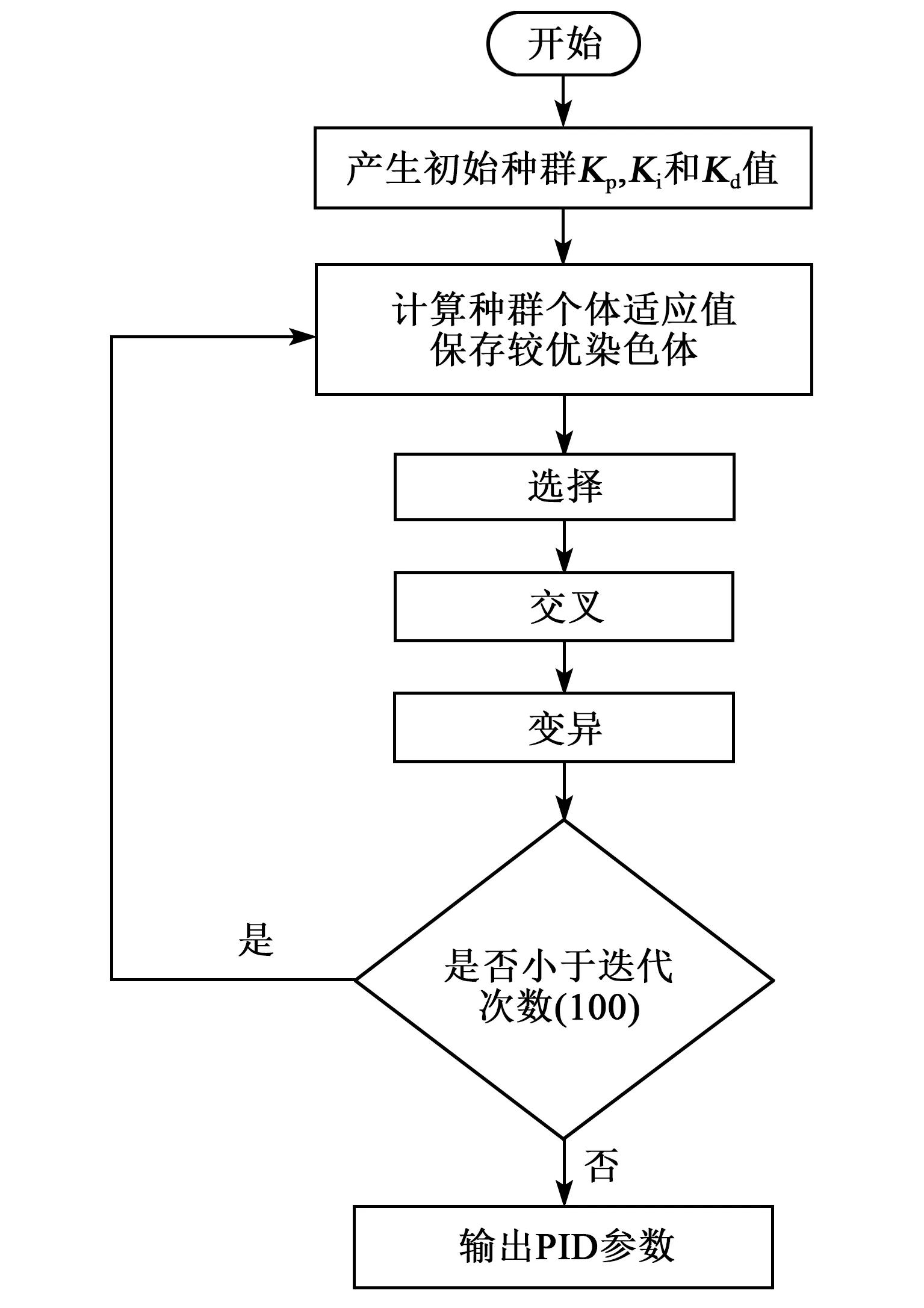
图7 遗传算法优化PID参数流程

图8 Simulink中的压电悬臂梁系统仿真

图9 控制系统

图10 PID优化曲线

图11 适应度函数优化曲线

初始状态时，给悬臂梁输入正弦力激励信号，使压电悬臂梁在一阶固有频率下振动。振动时，悬臂梁根部的应力产生较大变化，位于悬臂梁根部下端的压电陶瓷片因为应力的变化，产生传感信号。进行反馈控制前可将输出的传感信号乘以一个阶跃信号，以便更直观地表现控制效果。阶跃信号触发点设置在0.5 s时，在前0.5 s，由于阶跃信号为低电平，不会形成闭环反馈，是一种开环系统。当在0.5 s时形成高电平信号，开关闭合，产生反馈信号，信号经过控制系统后，计算得出控制电压信号反馈于悬臂梁根部上端的压电陶瓷片上，形成闭环控制系统。

3 系统仿真结果

3.1 压电执行器在悬臂梁根部

位移信号不涉及闭环反馈，只作为观测悬臂梁的振动抑制效果。根据传感器和执行器形成的闭环控制系统，如图12所示，在0.5 s时，阶跃信号由低电平跃变为高电平，此时系统由开环变为闭环反馈控制。可观测压电悬臂梁振动控制系统中的位移信号变化，0.5 s后加入控制策略，振动得到快速抑制，抑制效果可达92.4%。图13为悬臂梁端部振动位移信号。

图12 开环和闭环状态下的信号波形

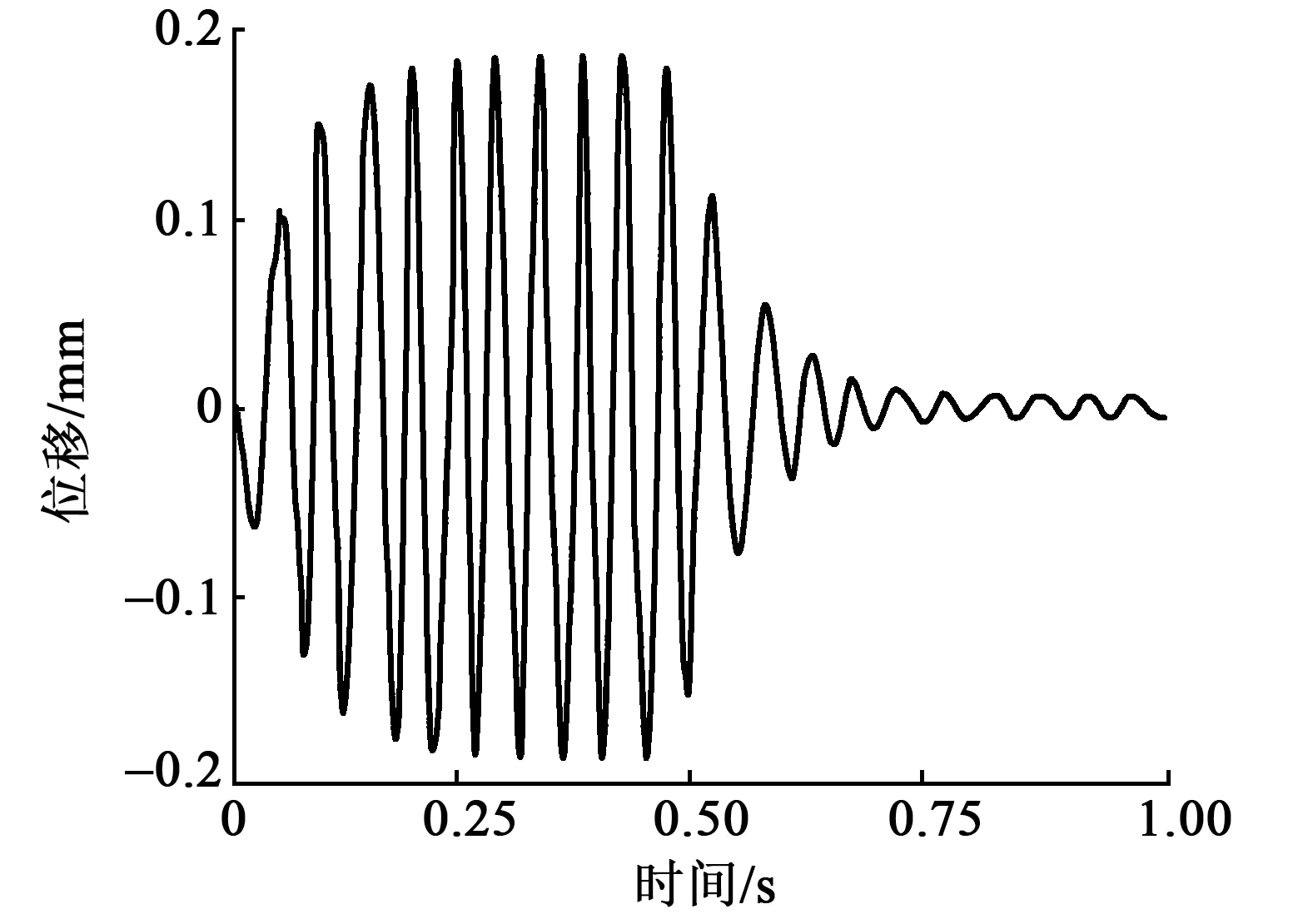
图13 悬臂梁端部振动位移信号

3.2 压电执行器在悬臂梁其他位置

针对工业工程上悬臂结构的振动控制问题，由于结构布局，起到控制作用的执行器可能无法位于根部的位置，此时需考虑悬臂梁其他部位是否同样具有良好的振动抑制效果。根据本文悬臂梁模型设计了执行器的4种不同的粘贴位置，依次从根部排至端部，定义不同位置依次为P1、P2、P3、P4，如图14所示。执行器(PZT1)间距固定为1 cm，固定传感器(PZT2)的位置不变，观测不同位置执行器控制效果。

图14 执行器的不同粘贴位置P1～P4

设计悬臂梁控制仿真系统，激励信号的频率设置为悬臂梁的一阶固有频率，添加50 mN力作用于点载荷，将仿真时间设置为1 s。针对4种粘贴在不同位置的执行器，应用遗传算法优化各位置PID参数，并实现振动控制仿真。致动器位于4种不同位置，其参数值对应不同的位移结果，不同的抑制效果。不同位置粘贴所对应参数值及振动抑制率如表3所示。

表3 PID优化后的参数及其抑制率

图15为P1～P4仿真位移结果。由图可看出，当仿真时间处于0.5 s后，压电悬臂梁系统处于闭环控制状态，悬臂梁可得到快速抑制。根据执行器的粘贴位置P1、P2、P3、P4，其抑制效果逐渐降低, 但均能获得超过50%的振动抑制率。靠近端部抑制效果较差，可能是因为多物理场软件本身存在过大电压倍数反馈输出，造成仿真过程中的解无法收敛。

图15 P1～P4仿真位移结果

4 振动抑制实验及结果分析

4.1 实验平台搭建

图16为基于遗传算法的悬臂梁振动抑制。为了验证基于遗传算法的PID整定方法可行性，搭建的PID算法模型控制平台如图17所示。实验基于Labview软件作为实验的控制平台，以搭载Labview软件的笔记本电脑作为上位机，NI-PXI系列采集卡作为下位机和采集设备。Labview是一种非文本化的编程软件，该软件采用框图式编程方式,是硬件在环控制系统的设计核心，与NI系列采集卡具有最佳的匹配兼容性。本文利用采集悬臂梁实验数据，应用遗传算法进行PID参数的整定，实现压电悬臂梁的在线实时主动振动控制。

图16 基于遗传算法的悬臂梁振动抑制

图17 基于遗传算法的PID控制实验平台

当压电悬臂梁处于一阶共振频率时，能量处于最大，是压电复合材料处于振动最复杂的状态。能否将一阶固有频率下的压电悬臂梁振动抑制是验证试验方法正确的关键。

激励源设计在压电悬臂梁的中部，以此来模拟外部环境的干扰。当由信号发生器产生信号经过功率放大器加载于PZT3时，悬臂梁会因为压电陶瓷片的压电效应，由电能向机械能转化，使悬臂梁振动。采集卡将PZT2电信号采集并进行模数转换将数据传输于上位机中进行算法处理计算，输出控制电压信号，信号进行数模转换，将采集卡输出电压信号反馈，经过功率放大器后反馈给PZT1，此时PZT1作为执行器使用，通过能量转换来抑制压电悬臂梁的振动。

实验分为两个阶段：

1) 开环阶段，即利用信号发生器激励压电悬臂梁的振动，模拟外界干扰，信号发生器给位于中部的PZT3施加峰值1.5 V、频率28.6 Hz的电压，其中28.6 Hz是悬臂梁实验实际的一阶共振频率，经过功率放大器驱动压电悬臂梁。

2) 闭环阶段。当压电悬臂梁受迫振动时，位于悬臂梁根部下端的压电陶瓷片经过遗传算法整定PID参数，系统带有误差反馈，并将误差线性组合反馈于位于根部上端的压电陶瓷片。

4.2 实验结果分析

图18为实验抑制效果。在5 s后加入PID控制，振动控制在7 s后快速达到动态平衡，压电悬臂梁处于稳定的振动抑制状态，且振动抑制较好，抑制效率可达77.8%。

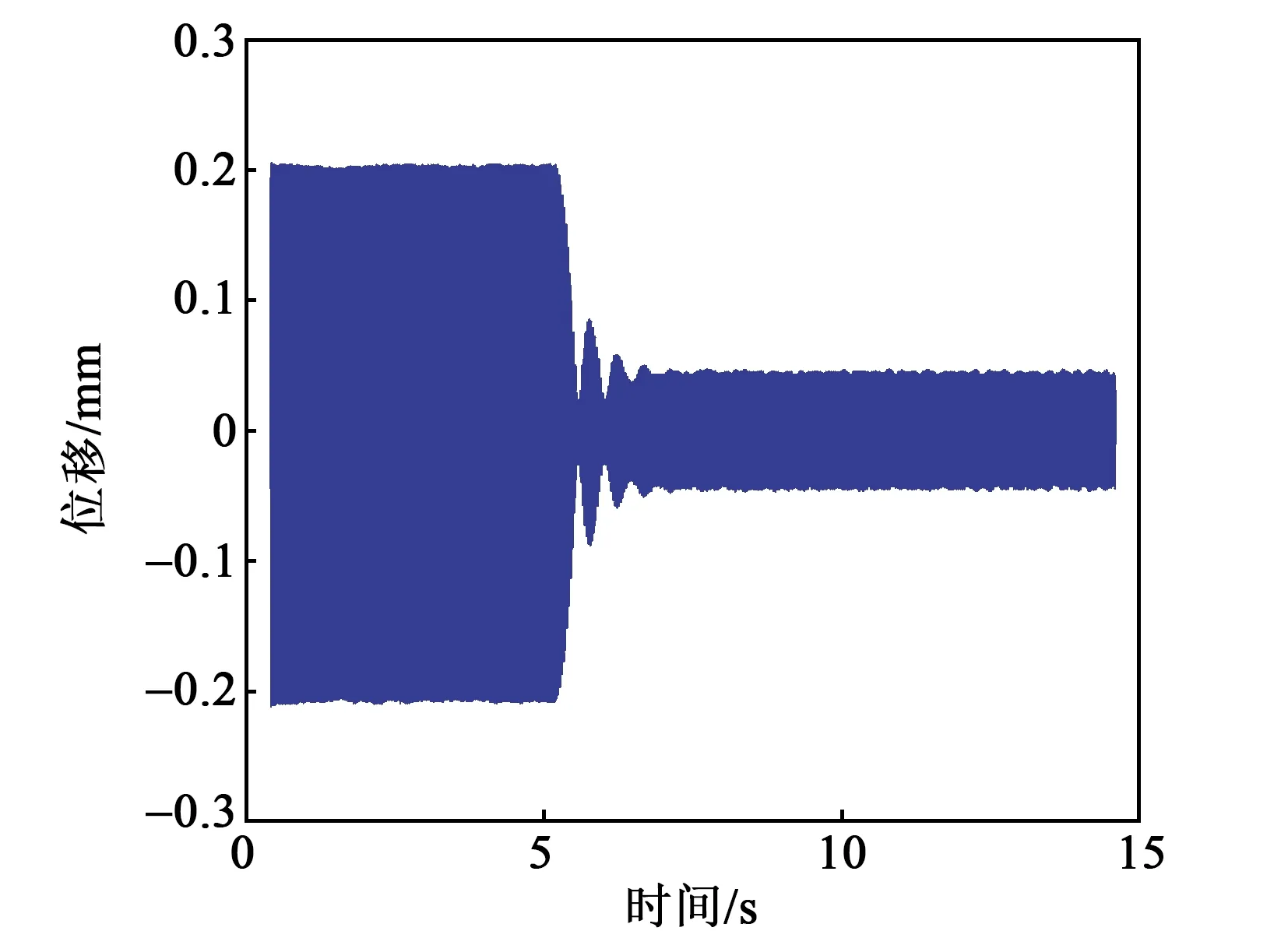
图18 悬臂梁根部抑制效果

与仿真一致，为了验证位于悬臂梁不同位置的压电执行器的抑制效率，设计了4种不同位置的压电陶瓷片粘贴位置，依次从悬臂梁的根部粘贴至悬臂梁的端部。在实验开始阶段，压电悬臂梁处于开环阶段，即只受信号发生器的激励作用，处于自由振动状态。闭合实验开关，使实验处于带有负反馈的闭环状态，即经过控制器计算控制信号输出，得到的仿真结果如图19所示。表4为P1～P4不同位置对应的参数值。

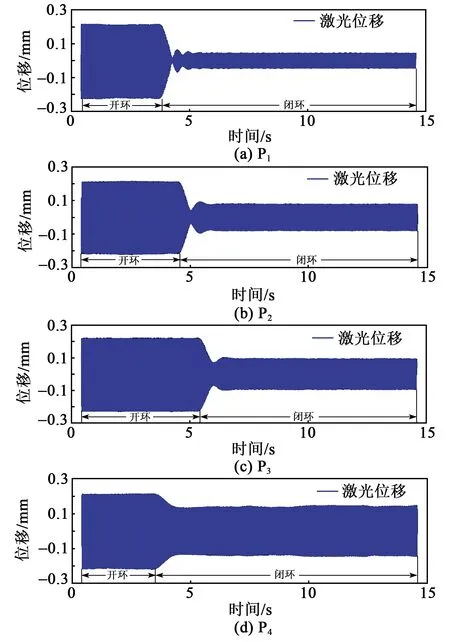
图19 P1～P4不同位置的压电执行器抑制结果

表4 P1～P4不同位置对应的参数值

如图19所示，由实验结果很容易得出，与仿真结果较一致，执行器位于悬臂梁的根部抑制效率最高。抑制效率从P1至P4位置依次递减，如图20所示。其中P4位置的抑制效率较低，抑制效果较差。由表4可看出，越靠近悬臂梁根部的压电致动器，抑制效果更佳，如在实际应用特定情况下，无法将压电致动器放置于悬臂梁根部位置，可选择将压电致动器放置于靠近根部或中部位置，同样具有良好的抑制效果。

图20 P1～P4位置抑制率

5 结束语

本文以抑制一阶共振频率下悬臂梁振动为目的，针对悬臂梁在建立动力学微分方程中的复杂性高、精确性较差等弊端，提出一种利用COMSOL多物理场软件与Simulink仿真软件相结合，建立悬臂梁振动控制系统联合仿真模型的方法。同时针对PID参数手动调整中的最优化问题，提出利用遗传算法来优化控制参数，根据该模型选择合适的遗传算法适应度函数，并应用于压电悬臂梁振动控制系统上。通过优化调整仿真结果显示，利用遗传算法优化的PID控制算法参数可有效地抑制悬臂梁在一阶共振频率下的振动。

针对压电执行器在悬臂结构的工业应用，可能无法将执行器粘贴于根部，通过仿真来验证执行器位于不同位置是否仍具有良好的抑制率，仿真和实验结果证明越靠近悬臂梁根部，抑制效果越好，但其他位置同样具有一定的抑制效果，可根据工业悬臂结构应用中的实际需求灵活放置致动器。