一种改进的补偿因子区域不变CS算法及Simulink模型建模

宋栩潮，周 鹏，张振华，肖忠源

（1 中国石油大学（华东）海洋与空间信息学院 青岛 266580；2 北京遥测技术研究所 北京 100076）

引言

传统实时SAR（Synthetic Aperture Radar，合成孔径雷达）成像系统架构大都采用FPGA（Field-Programmable Gate Array，现场可编程门阵列）与DSP（Digital Signal Processor，数字信号处理器）相结合的架构[1−3]。其中，FPGA主要用于实现数据采集和预处理，DSP 主要用于实现SAR 成像算法[4]。近年来，随着FPGA 器件的快速发展，以及其在星上特殊环境下具有优于DSP 的抗单粒子翻转能力，采用FPGA 逐步替代DSP 来实现SAR 成像算法，成为星上SAR 实时成像系统的重要研究方向之一[5−7]。

然而，算法设计人员在进行FPGA 程序开发时常会受到以下限制[8−11]：①算法设计人员通常不熟悉硬件描述语言，导致开发周期长；②FPGA的并行程序设计与基于Matlab 或DSP 的串行程序设计有很大的差异。而利用Simulink 工具实现FPGA 快速开发的方式则较好地解决了上述问题[12]。算法设计人员利用Matlab 验证算法的正确性后，可利用Simulink 搭建算法模型并自动转换为FPGA 代码，大大降低了FPGA 开发的难度、提高了开发效率。另外，当算法需要改进时，只需要在Simulink模型对应的模块上进行修改，通过自动生成硬件语言即可实现算法的改进，灵活性较强。

CS 算法是合成孔径雷达实时成像处理中常采用的一种算法。在经典CS 算法的处理过程中，涉及到相位补偿、距离向补偿和方位向补偿这三种补偿因子的计算。这些补偿因子涉及到正余弦和开根号等超越运算，采用FPGA 实现这些计算需要较长的运算时间和很大的存储空间。若对于数据矩阵中的每条数据都要更新补偿因子，则严重影响SAR 成像处理的实时性。针对上述问题，文献[13]提出一种具有补偿因子区域不变特点的CS 算法，其特点是区域内的各条数据采用固定的补偿因子。该方法在少量损失了三种补偿因子精度的情况下大幅减少了计算量，提高了处理效率。但在该方法中，区域内的统一补偿因子采用的是区域内第一条数据对应的补偿因子，会造成相位补偿误差不均匀的问题。

针对上述问题，本文对文献[13]中的方法进行了改进，将区域内的统一补偿因子改用该区域内所有单元频率平均值对应的补偿因子进行代替，使得采用统一补偿因子造成的相位误差在区域内更加均匀。显然，改进算法与原有算法的计算量相当。但由于改进后算法对应的相位误差在区域内更加均匀，使得改进算法的成像质量得到提升。为此，首先开展了Matlab 仿真工作，验证了改进后算法相比于原有算法在成像指标方面的提升。接下来，搭建了用于生成改进算法中三种补偿因子的Simulink模型。之后，将Simulink模型输出的代码加载到Vivado 软件中，通过对比Vivado 软件输出的补偿因子和Matlab 软件输出的精确补偿因子，验证了所搭建Simulink模型的高精度。

1 补偿因子区域不变CS 算法的改进及Matlab验证

1.1 经典CS算法原理

雷达发射信号一般为LFM（Linear Frequency Modulated，线性调频）信号。对去载频后的点目标回波信号进行方位向FFT（Fast Fourier Transform，快速傅里叶变换），可得信号在距离多普勒域的表达式为[14]：

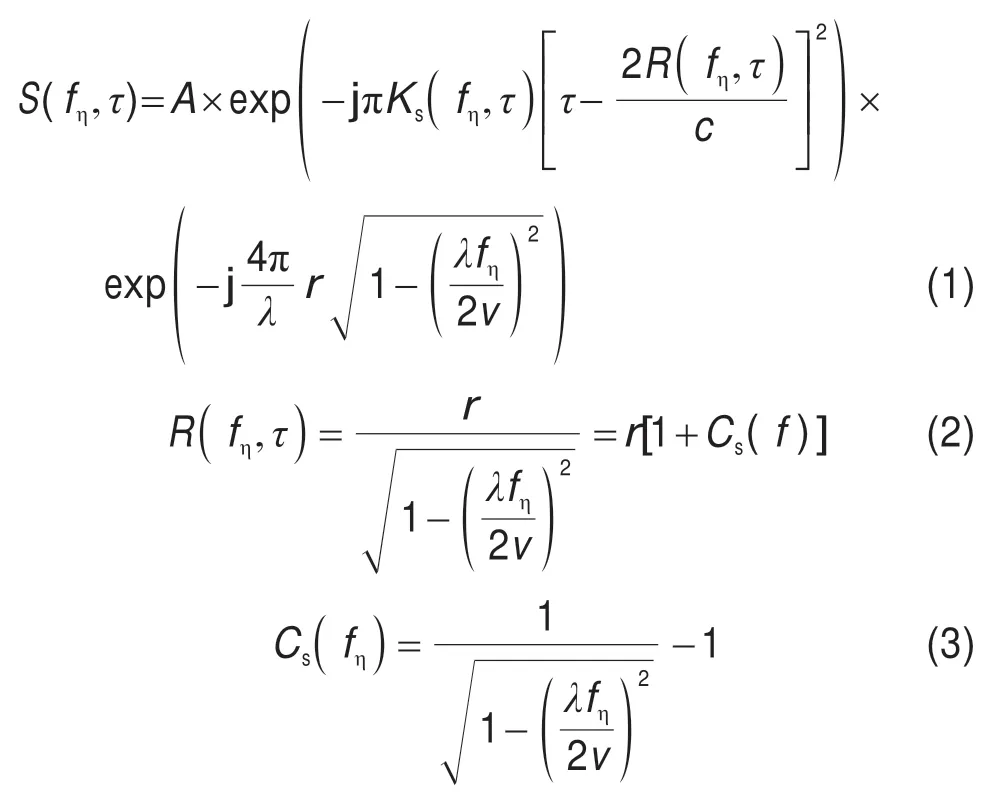
式中，τ表示距离向快时间，fη表示方位向频率，r表示雷达与点目标的距离，A表示调幅项，包括目标后向散射系数、距离向天线方向图和方位向天线方向图等因素的影响，Ks表示距离信号多普勒域调频率因子，c表示光速，λ表示雷达发射脉冲信号波长，v表示平台飞行速度，Cs表示距离弯曲因子。

为使在不同距离上的移动轨迹都与在参考距离上的移动轨迹一致，需对式(1)乘以如下CS 相位补偿因子：

式中，rref表示参考距离。

对乘以相位补偿因子后的信号进行距离向FFT，将信号转换至二维频域，然后将信号二维频域表达式乘以距离向补偿因子，完成距离压缩、二次距离压缩和距离徙动校正。距离向补偿因子的表达式为：

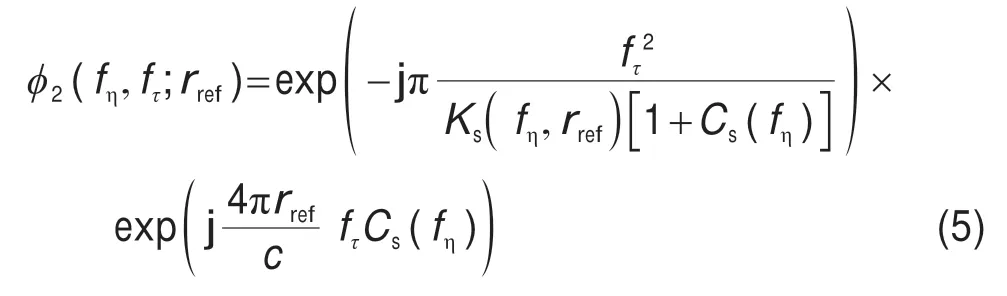
式中，fτ表示距离向频率。

将二维频域信号与式(5)相乘后进行距离向IFFT，再乘以方位向补偿因子后完成方位压缩和残余相位补偿。方位向补偿因子的表达式为：

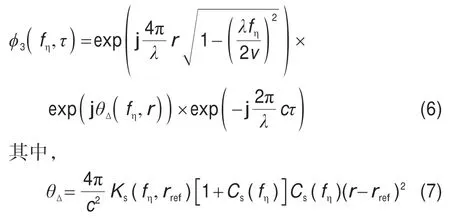
再将乘以方位向补偿因子后所得的信号进行方位向IFFT（Inverse Fast Fourier Transform，快速傅里叶逆变换），即可得到目标图像。

为方便在FPGA 上实时生成三种相位因子，需要对fη、fτ进行量化处理。将fη等分为Nη份，将fτ等分为Nr份（Nη和Nr分别表示方位向和距离向点数），即

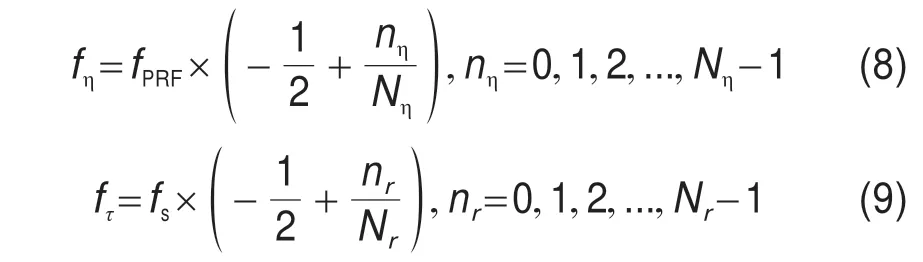
式中，fs表示雷达信号采样频率，fPRF表示脉冲重复频率。

CS算法的成像质量与式(4)、式(5)和式(6)表示的三种补偿因子的精度有直接关系，因此在实际应用中，补偿因子计算模块的精度非常重要[15]。

1.2 补偿因子区域不变CS算法的原理

CS 算法成像过程中含有三种补偿因子的计算，且每种补偿因子都需要与对应的数据矩阵进行复乘。同时CS 成像算法中补偿因子的计算比较复杂，包括正余弦和开根号等多种超越运算，采用FPGA 实现需要较长的运算时间和很大的存储空间，对SAR 成像处理系统的实时性产生较大影响。

针对上述问题，文献[13]中提出一种具有补偿因子区域不变特点的CS 算法，即选定一个更新步长∆n=2n（n为正整数），每个更新步长内只计算第一个距离向或方位向的补偿因子，将后几个距离向或方位向的补偿因子用其替换。该文中指出：∆n越大，在区域内采用统一的补偿因子带来的误差也越大；当∆n不超过16 时，三种误差均不超过6×10-5。该算法使得三种补偿因子的计算量大幅降低，从而有效减少补偿因子的计算时间及其占用的存储器资源。该算法的原理如图1所示。

图1 补偿因子区域不变CS算法的处理流程图Fig.1 Flow chart of a chirp scaling algorithm featured by invariance of compensation factors in a region

对于补偿因子区域不变CS 算法，在一个更新步长内，其统一补偿因子满足如下特点：

1.3 改进的补偿因子区域不变CS算法

在1.2 节所述的现有算法中，对于更新步长内各单元的统一补偿因子，使用的是第一个单元对应的补偿因子。在该算法中，对于更新步长内首行/列的相位误差为0，但后续的每个距离向和方位向单元对应的误差会逐渐增加，导致补偿后的相位误差在区域内分布不均匀。

针对上述问题，本文对文献[13]中的算法进行了改进，将一个更新步长内的统一补偿因子，采用区域内所有单元频率平均值对应的补偿因子进行代替。相比于改进前的算法，在更新步长对应的区域内，中间单元对应的误差最小，第一个和最后一个单元对应的误差最大，补偿结果的相位误差在区域内更加均匀。

对于改进后的补偿因子区域不变CS 算法，在一个更新步长内，其统一补偿因子对应的频率值满足如下特点：

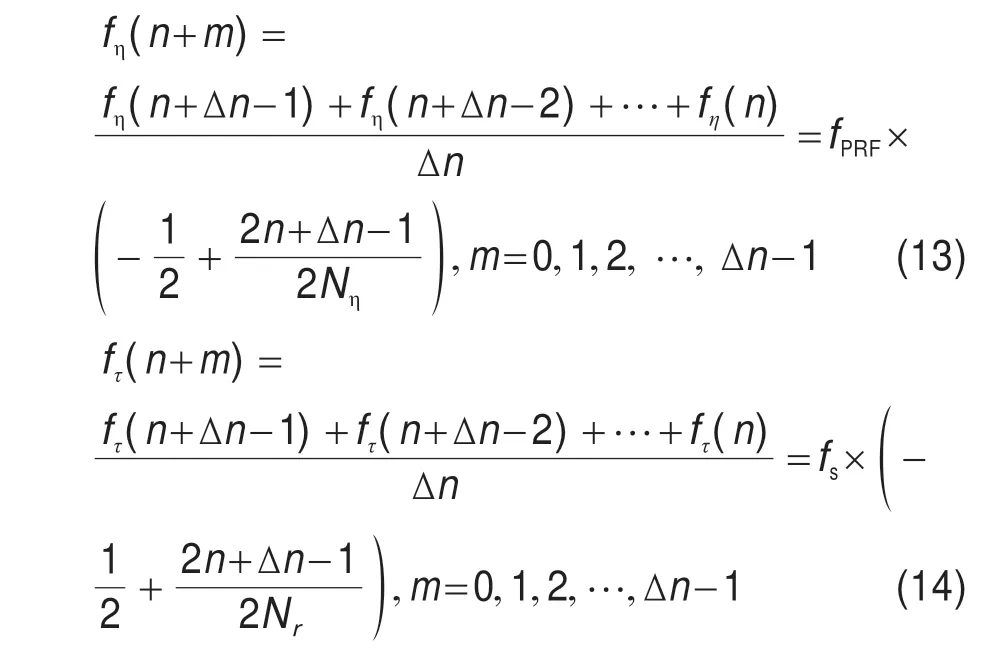
在FPGA 实现CS 成像算法的过程中，会频繁地从存储器中读取提前存储好的补偿因子，影响处理效率。经典CS 算法在进行补偿因子的复乘操作时，每进行一次复乘都需要给存储器发送地址来读取该地址下的数据，而改进后的补偿因子区域不变CS 算法只需要每隔一个更新步长取出一次数据即可，大大降低了进行复乘操作时的存储器读写频率，同时节约了存储器资源，相比于经典CS 算法更易于FPGA 实现。在实际应用时，只要在成像之前完成所有补偿因子的计算并存入存储器中即可，不会占用成像时间。改进算法相比于文献[13]中的算法，计算量相当。由于最终的补偿结果相比于文献[7]中算法的补偿结果更加均匀，成像质量将有一定提升。下面对改进算法中3种补偿因子的相位误差进行量化分析。

1.4 改进算法中3种补偿因子的相位误差分析

式(4)～式(6)中的Ks和Cs仅随方位向频率变化，而雷达有效速度v和方位向频率fη在距离向不发生变化，因此v和方位向频率fη不受更新步长的影响；而τ和r是随着距离单元变化的，即：

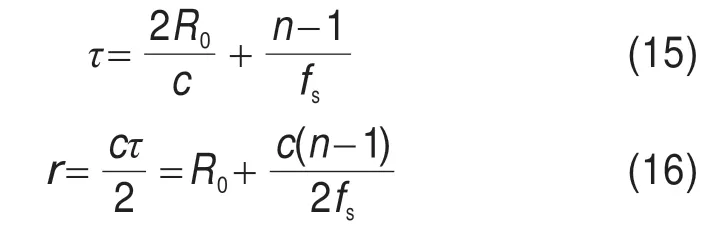
式中，R0表示最近斜距。在一个更新步长内，相位因子的最大相位误差为：

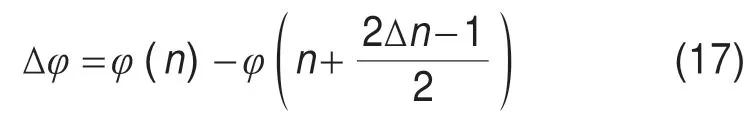
下面对三种补偿因子的相位误差进行量化分析。

1.4.1 CS相位补偿因子的相位误差

由式(4)、式(15)可得，第n个距离单元内的CS相位补偿因子的相位可以表示为：

在一个更新步长内，对应的最大相位误差∆φ1为：

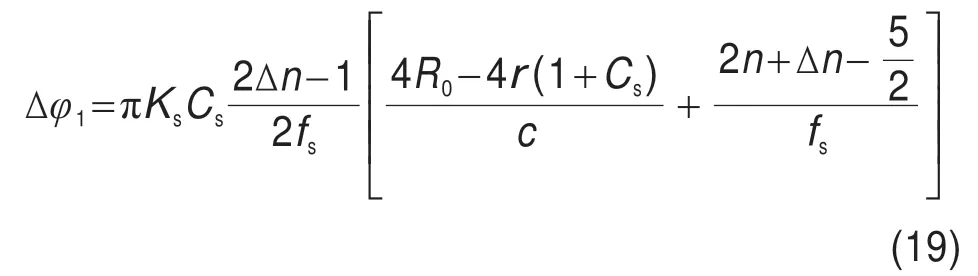
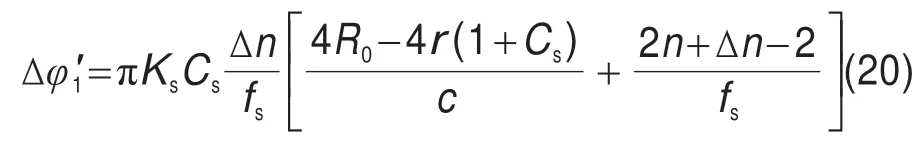
下面通过仿真，对两种算法的最大相位误差进行比较。仿真参数设置为：雷达发射信号频率为5.3×109Hz，场景中心斜距为2 000 m，雷达有效速度为150 m/s，距离向调频率为2×1013Hz/s，距离向采样率为6×107Hz，方位向采样率为200 Hz，距离向采样点数为640，方位向采样点数为2 048。两种算法最大相位误差随更新步长变化的仿真结果见表1。可以看出，改进算法的最大相位误差小于原始算法的最大相位误差。

表1 CS相位因子最大相位误差随更新步长的变化Table 1 Variation of maximum phase error of chirp scaling phase factor with the update step size

1.4.2 距离向补偿因子的相位误差

由式(5)可得，第n个方位单元内的距离向补偿因子的相位可以表示为：

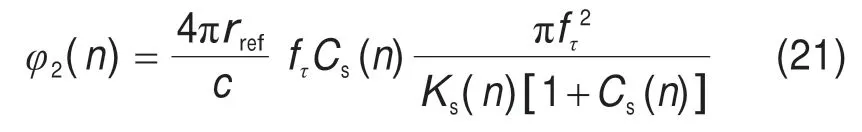
在一个更新步长内，对应的最大相位误差∆φ2为：

利用与前文相同的参数进行了仿真，两种算法最大相位误差随更新步长变化的仿真结果见表2。可以看出，改进算法的最大相位误差小于原始算法的最大相位误差。

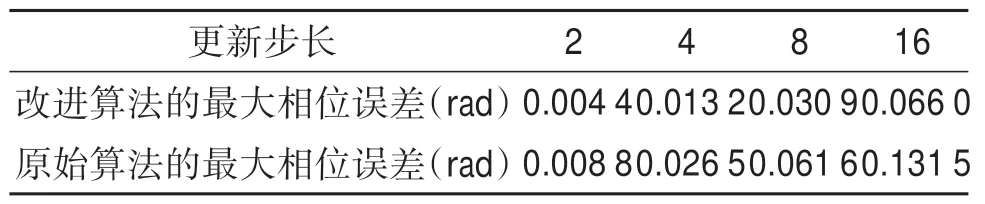
表2 距离向补偿因子最大相位误差随更新步长的变化Table 2 Variation of the maximum phase error of the range compensation factor with the update step size

1.4.3 方位向补偿因子的相位误差

由式(6)、式(16)可得，第n个距离单元内的方位向补偿因子的相位可以表示为：

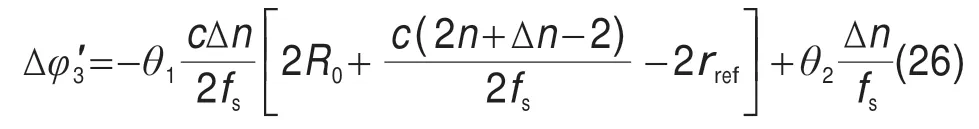
利用与前文相同的参数进行了仿真，两种算法最大相位误差随更新步长变化的仿真结果见表3。可以看出，改进算法的最大相位误差小于原始算法的最大相位误差。

表3 方位向因子最大相位误差随更新步长的变化Table 3 Variation of maximum phase error of the azimuth compensation factor with the update step size

1.5 三种CS算法的Matlab验证

对经典CS算法、补偿因子区域不变CS算法和改进的补偿因子区域不变CS 算法，采用Matlab 语言编制程序，分别对点目标仿真回波和实测数据进行了成像处理。其中，对点目标的成像指标采用距离向和方位向峰值旁瓣比、积分旁瓣比和分辨率进行比较，对实测数据的成像结果采用均方根误差进行比较。由于FPGA 本身进行浮点数运算会存在误差，更新步长的值不宜偏大，因此本文中假设更新步长等于4。

1.5.1 点目标仿真成像

首先，以更新步长等于4的情况为例，分别采用经典CS算法、补偿因子区域不变CS算法以及改进的补偿因子区域不变CS 算法，对点目标仿真回波数据进行了成像处理，得到详细的成像结果及成像指标。在处理原始数据时，在方位向加矩形窗以对天线双程方向图的数据范围进行限制。仿真参数设置如下：发射信号脉宽为2.5×10-6s，雷达发射信号频率为5.3×109Hz，场景中心斜距为2 000 m，雷达有效速度为150 m/s，距离向调频率为2×1013Hz/s，距离向采样率为6×107Hz，方位向采样率为200 Hz，距离向采样点数为640，方位向采样点数为2 048，波束方向为正侧视。成像过程中三种算法均未进行加窗处理。图2、图3 和图4 分别给出了三种算法的点目标成像结果、距离向剖面图和方位向剖面图。观察图2、图3 和图4 中的剖面图与成像结果图可以看出，三种算法对点目标的成像质量都很高。

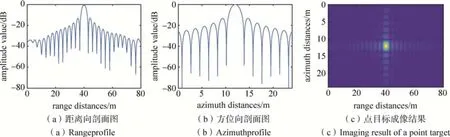
图2 经典CS算法的点目标成像结果Fig.2 Imaging results of a point target by the traditional CS algorithm

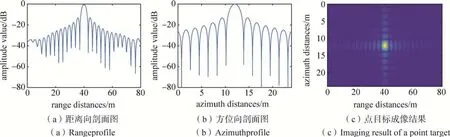
图3 补偿因子区域不变CS算法的点目标成像结果Fig.3 Imaging results of a point target by the CS algorithm featured by invariance of compensation factors in a region

图4 改进的补偿因子区域不变CS算法的点目标成像结果Fig.4 Imaging results of a point target by the improved CS algorithm featured by invariance of compensation factors in a region

为便于对三种算法的性能进行定量比较，分别计算了距离向和方位向的峰值旁瓣比、积分旁瓣比和分辨率，列于表4和表5。

表4 点目标仿真结果的距离向成像性能指标Table 4 Imaging performance indexes of a point target's result in range direction

表5 点目标仿真结果的方位向成像性能指标Table 5 Imaging performance indexes of a point target's result in azimuth direction

为了比较改进前、后两种算法在更新步长较大情况下的成像质量，分别采用改进前、后两种补偿因子区域不变CS 算法，在更新步长等于8、16 的情况下对点目标进行了成像处理，成像结果如图5和图6所示，成像指标列于表6和表7。仿真参数设置与更新步长等于4的情况一致。

图5 改进前后两种补偿因子区域不变CS算法的点目标成像结果（∆n=8）Fig.5 Imaging results of point targets with original and improved compensation factor region invariant CS algorithm（∆n=8）

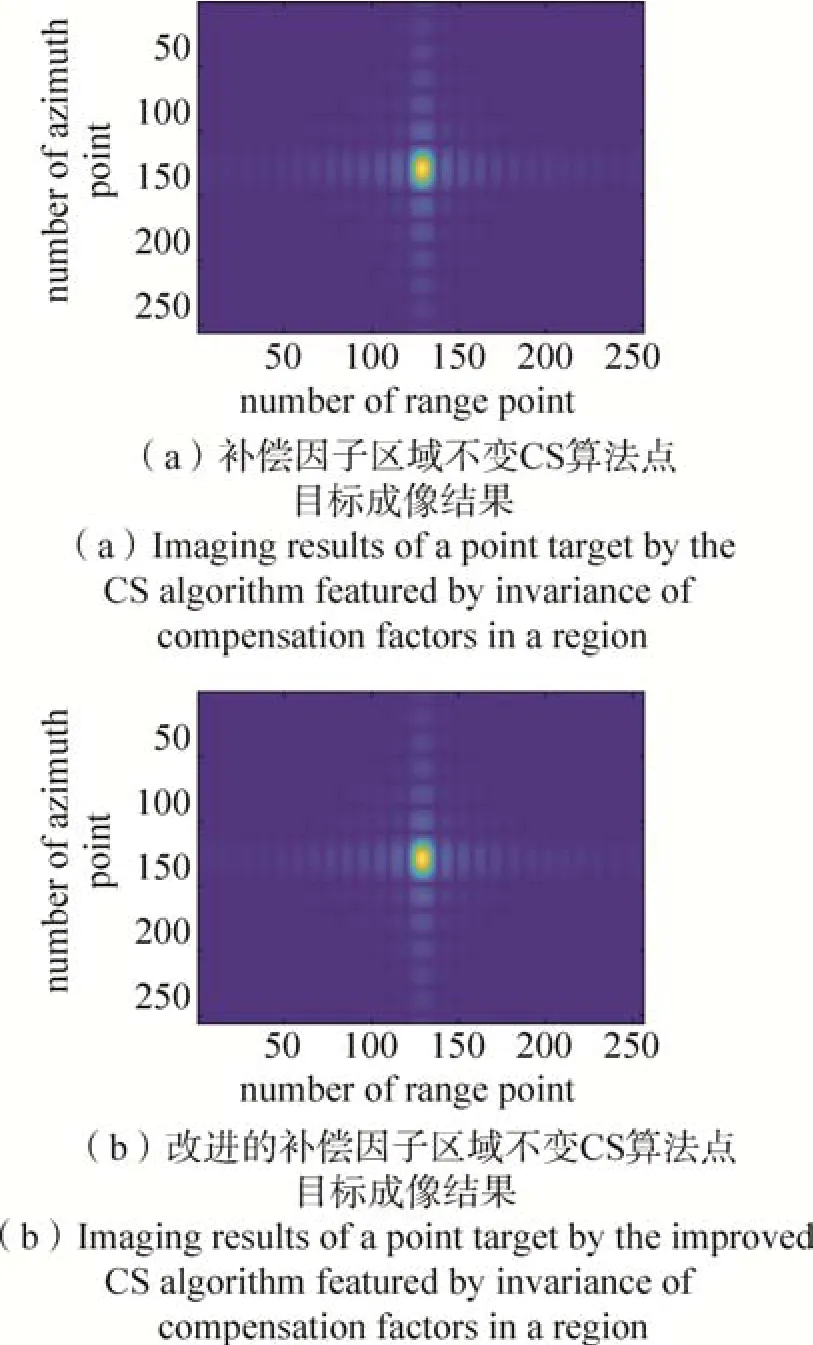
图6 改进前后两种补偿因子区域不变CS算法的点目标成像结果（∆n=16）Fig.6 Imaging results of point targets with original and improved compensation factor region invariant CS algorithm（∆n=16）

对比图2、图3、图4 和表4、表5 中数据可发现：三种算法的成像质量较为接近。其中，经典CS 算法的成像指标最佳。但需说明的是，尽管经典CS 算法的指标最佳，但与另两种算法的指标相比提升有限，而其付出的代价是运算复杂度高。相比于补偿因子区域不变CS 算法，改进后算法的成像性能指标有提升。

对比表6、表7 中数据可以看出，随着更新步长的增大，改进后算法的成像性能指标相比改进前的指标，其提升会更加明显，进一步体现了在数据量大、硬件资源有限进而需要选取更大的更新步长的情况下，改进后算法相比于原始算法有更大优越性。

表6 点目标仿真结果的成像性能指标（∆n=8）Table 6 Imaging performance performance of a point target's result（∆n=8）

表7 点目标仿真结果的成像性能指标（∆n=16）Table 7 Imaging performance of a point target's result（∆n=16）

1.5.2 实测数据成像

实测数据采用一组来源于RADARSAT-1 卫星的某海岸线周边区域的回波数据，令更新步长等于4，得到经典CS 算法、补偿因子区域不变CS 算法和改进的补偿因子区域不变CS 算法的成像结果如图7所示。

图7 3种算法对RADARSAT-1原始数据的成像结果Fig.7 Imaging results of three algorithms on raw data of RADARSAT-1

以经典CS 算法的成像结果为基准值，分别以补偿因子区域不变CS 算法和改进的补偿因子区域不变CS 算法的成像结果作为对比值，计算出两种算法的均方根误差指标。从表8数据可以看出，相比于改进前算法，改进后算法的成像性能指标得到提升。

表8 补偿因子区域不变CS算法和改进的补偿因子区域不变CS算法的均方根误差Table 8 Mean root squares of the previous and the improved CS algorithms featured by invariance of compensation factors in a region

2 改进算法中补偿因子计算模块的结构设计和Simulink模型

2.1 补偿因子计算模块的结构设计

本文采用乒乓工作机制对改进算法中用于计算补偿因子的模块进行了设计，其信号实时处理能力是单个补偿因子模块的两倍。当有数据输入时，该结构采用了乒乓处理原理，将数据分别输入通道1 和通道2 中，在输出端对处理结果进行乒乓接收。图8 和图9 分别给出了所设计的补偿因子计算模块的乒乓结构示意图和时序图。

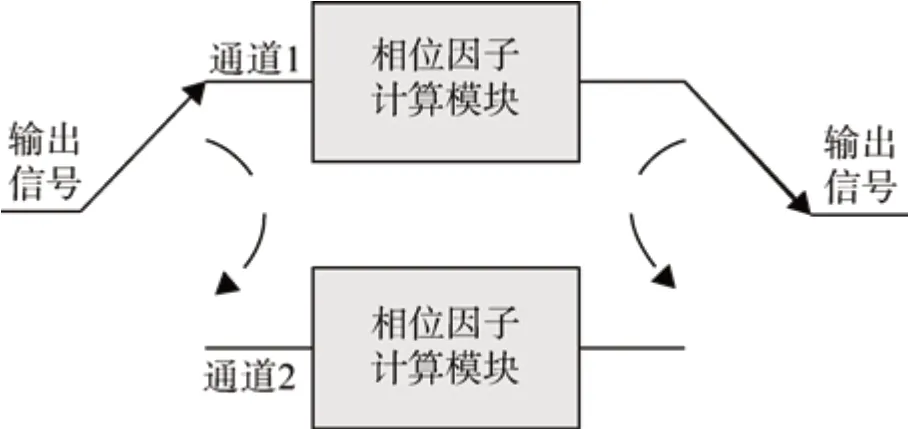
图8 补偿因子计算模块的结构示意图Fig.8 Structure diagram of the designed module for calculating compensation factor

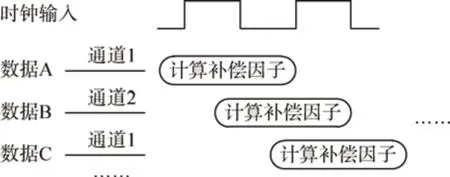
图9 补偿因子计算模块的时序图Fig.9 Timing diagram of the designed module for calculating compensation factor

2.2 补偿因子计算模块的Simulink模型搭建

所搭建的三种补偿因子计算模块的Simulink模型分别如图10(a)～图10(c)所示。为了节约硬件资源，Simulink模型中所有输入、输出和中间变量的数据格式均采用32 bit 的单精度浮点数，数据格式中有7位有效数字。

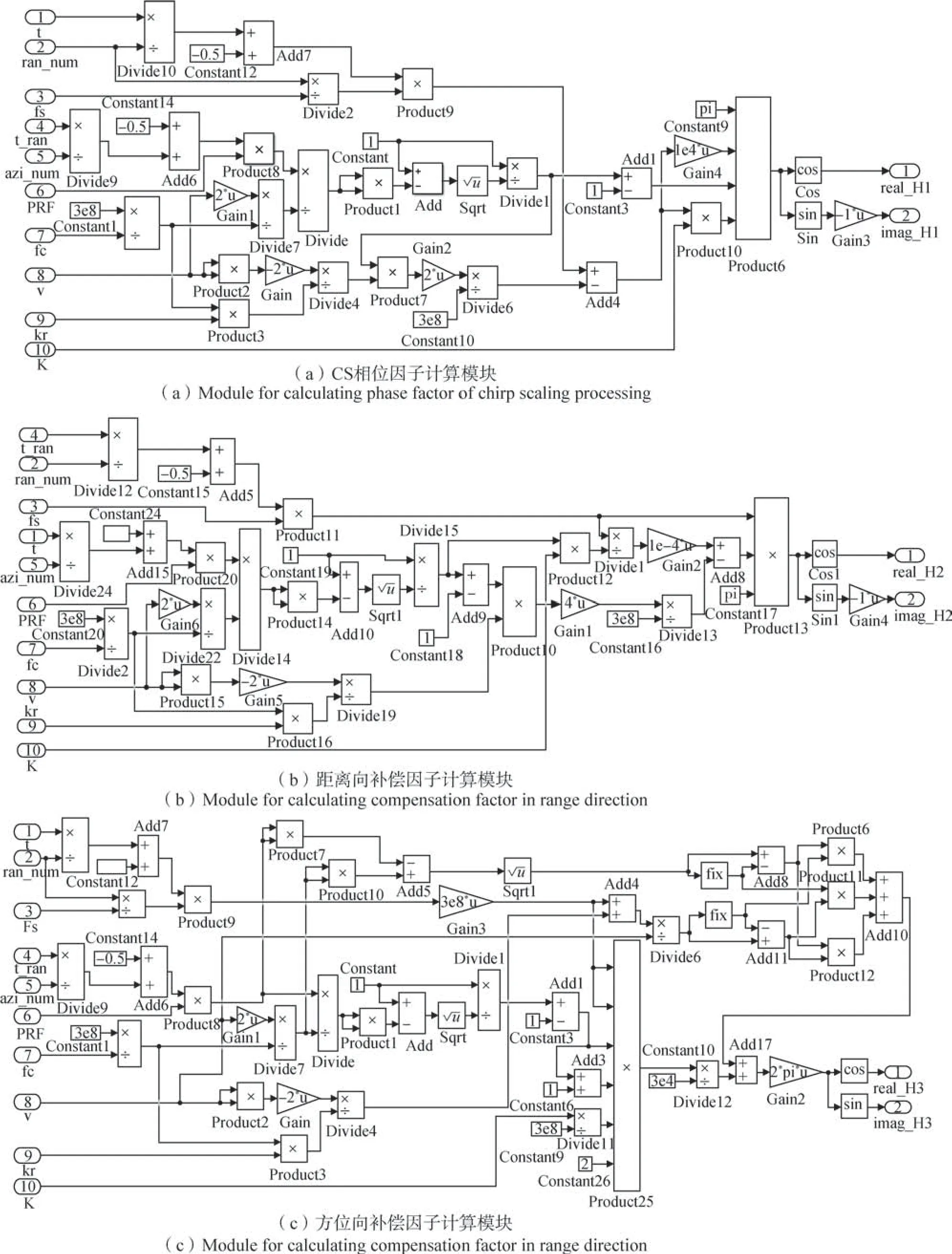
图10 三种补偿因子计算模块的Simulink模型图Fig.10 Three Simulink models for calculating compensation factors

需注意的是，在补偿因子的计算过程中，某几个中间变量相乘后的值会非常大，使得整数部分占有较多的有效数字个数，从而导致产生较大的计算误差。因此，为减小上述误差来源，需对模块中的部分组成进行专门的设计。下面以方位向补偿因子计算模块的部分组成为例进行说明。

在方位向补偿因子计算模块中，先提出了2π作为指数项的公因子，使得最终补偿因子的计算结果仅取决于输入数据的小数部分，再对计算过程中两个带有小数的中间变量相乘的项采用如图11 所示的子模块代替。图11 中，fix 表示向0 靠拢取整，a、b表示输入的被乘数，c表示乘数。通过该子模块的专门设计，可使得两个较大的含小数中间变量相乘后，整数部分占有的有效数字个数减少，从而提高最终计算结果的精度。

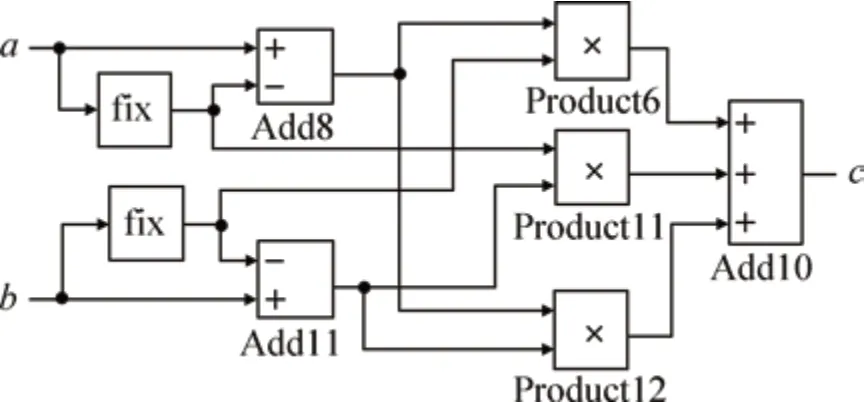
图11 用于计算小数部分的子模块Fig.11 Sub module for calculating decimal part

3 实验结果

仿真参数设置如下：脉冲重复频率为1 400 Hz，信号采样频率为3×107Hz，发射信号中心频率为109Hz，发射信号距离向调频斜率为2×1012Hz/s，雷达有效运动速度为1 000 m/s，距离向点数为1 024，方位向点数为1 024，方位向信号的多普勒调频率为-8 357 Hz/s。

根据上述仿真参数，执行如图8 所示的三个Simulink 模块并输出FPGA 代码。将Simulink 模型输出的代码加载到Vivado软件中进行执行。图12给出了Vivado软件输出的三种补偿因子的部分结果。

图12 Vivado软件的部分仿真结果Fig.12 Partial simulation results by Vivado software

利用Vivado 软件将补偿因子的计算结果存入txt 文件，然后由Matlab 读取并将结果转换为十进制小数存入.mat 文件中，每个补偿因子的实部和虚部分别构成一个矢量。编写改进的补偿因子区域不变CS 算法的Matlab 程序，输出正确的补偿因子仿真结果，每个补偿因子的实部和虚部分别构成一个矢量。将Vivado 输出的补偿因子与由Matlab 输出的精确的补偿因子进行相减，图13 给出了三种补偿因子实部和虚部的误差。

图13 Vivado输出结果相比于Matlab输出结果的误差Fig.13 Error of Vivado output result compared with Matlab output result

从图13 可以看出，CS 相位补偿因子的误差在±(2×10-3)以内，距离向和方位向补偿因子的误差在±0.01 以内，误差均较小，验证了本文所搭建Simulink 模型的准确性。其中，CS 相位补偿因子和距离向补偿因子的误差曲线图具有明显对称性，且越靠近成像场景中心的补偿因子对应的误差越小，体现了本文所提出改进算法的特点。

4 结束语

对一种具有补偿因子区域不变特点的CS 算法进行了改进，对于更新步长内各单元的统一补偿因子，采用该区域内所有单元频率平均值对应的补偿因子代替原来使用的第一个单元对应的补偿因子，使得采用统一补偿因子造成的相位误差在区域内更加均匀。原算法与改进后的算法计算量相当。经过Matlab 仿真验证，改进算法的成像指标得到提升，且更新步长越大，改进算法的性能提升越明显。为提高FPGA 代码的生成效率，采用Simulink工具搭建了用于生成改进算法中的三种补偿因子模型。将Simulink 模型输出的代码加载到Vivado 软件中，通过对比Vivado 输出的补偿因子与由Matlab 输出的精确补偿因子，验证了所搭建Simulink 模型的高精度。本文所研究的利用Simu‐link 建模生成FPGA 代码的方法具有较好的通用性，可推广应用至SAR 实时成像或其他电子信息领域，提高FPGA代码的生成效率。