基于贝叶斯理论的再生混凝土强度预测模型优势分析

骆岩松 李学祺 梁月清 李 灏 安邦国

（桂林理工大学土木与建筑工程学院，广西 桂林 541004）

0 引言

近年来我国建筑行业迅速发展，建筑废料的年产量高达20亿吨，其中包含大量的混凝土废料。对于建筑废料，尤其是混凝土废料的二次利用引起我国相关研究人员的高度重视。配合比设计一直是再生混凝土研究的重要环节，目前我国仍以试验方法确定混凝土配合比，这不仅浪费大量人力资源，还浪费大量原材料。为简化配合比设计流程，各国学者基于各类理论建立了混凝土强度预测模型。

混凝土成分复杂，导致其强度具有较大的离散性，预测难度大。李红[1]基于BP、RBF神经网络理论，对普通混凝土的强度进行预测，预测结果与实际结果相对误差均不超过6%；张静[2]提出CPSO-LSSVM的混凝土预测模型，对于所有类型混凝土的强度，该模型的平均预测精度均在95%以上。但神经网络模型解释性较差、计算成本较高，SVM预测精度取决于参数选取，而且仅在小样本领域有较好效果。而贝叶斯回归模型克服了以上缺点，基于贝叶斯理论建立的预测模型，解释性强、计算成本低，对大样本和小样本数据均适用，因而在建筑工程领域应用广泛。李宗坤[3]基于动态贝叶斯网络对混凝土坝失事风险概率进行评估，实现贝叶斯动态信息更新，更新结果接近真实结果；脱俗[4]结合先验信息和贝叶斯理论，建立了钢筋再生混凝土梁受剪承载力预测模型，具有较好的准确性；宋彦朋[5]基于贝叶斯原理提出钢筋混凝土梁有限元模型，具有很好的鲁棒性和灵活性。但在再生混凝土强度预测领域和再生混凝土配合比设计方面，贝叶斯理论应用较少，存在较大的研究发展空间。

本文以再生混凝土组成成分及比例为控制变量，综合考虑材料特性以及实验条件等因素的影响，基于贝叶斯理论建立再生混凝土强度预测模型，并与最小二乘回归模型和BP神经网络模型进行对比分析，探究贝叶斯回归预测模型在再生混凝土强度预测上的优势，尤其是在鲁棒性与自适应性上的优势，该研究对再生混凝土的发展和工程建设应用具有重要的参考价值。

1 再生混凝土强度预测模型建立

1.1 贝叶斯回归预测模型

混凝土的强度容易受到材料特性、养护条件、统计误差、变量缺失和试验条件[6]等各种不确性因素的影响，这些因素一直是影响再生混凝土强度预测研究的主要难点。贝叶斯理论综合考虑主客观不确定性影响，因此可应用于再生混凝土强度的预测。

贝叶斯理论是以已知信息的先验概率p(θ)为基础，实现对后验概率p(θ|y)的计算方法(式1)。贝叶斯回归是贝叶斯理论在回归分析中的一种应用，贝叶斯回归具有较强的“自适应”性，在处理大样本和小样本数据问题中具有优异的表现，能够有效防止因样本量的限制导致的过拟合问题，这是区别于最小二乘法实现回归参数估计的重要特点。

1.2 多元非线性预测模型

目前关于混凝土强度预测的模型还包括线性模型和非线性模型。李松[7]等以多元线性回归理论为基础建立混凝土强度预测的多元非线性回归模型，模型公式如式（2）：

式中：xi,xj——因变量；

ai,aj——回归系数；

fi(xi)——关于因变量的以函数；

C——截距。

以上述模型为基础，利用贝叶斯参数估计法和最小二乘法实现对回归系数的求解。

1.3 线性回归预测模型

同时，对比分析上述模型与主流混凝土强度预测模型（BP神网络模型和线性回归模型），以阐释贝叶斯回归模型的可行性和鲁棒性。其中，线性模型表达式如式（3）：

式中：ai——回归系数；

C——截距。

2 预测模型计算数据选取

数据来源于文献[8]，计算数据主要包括混凝土的各组成成分（水、水泥、砂、再生骨料）用量与混凝土的实际强度，数据的样本总量为46；混凝土强度范围在15~60MPa，水灰比范围在0.30~0.55。按照公式xi xw（xi为其他成分的实际用量，xw为水的实际用量）将数据转化为比例形式，如表1所示。

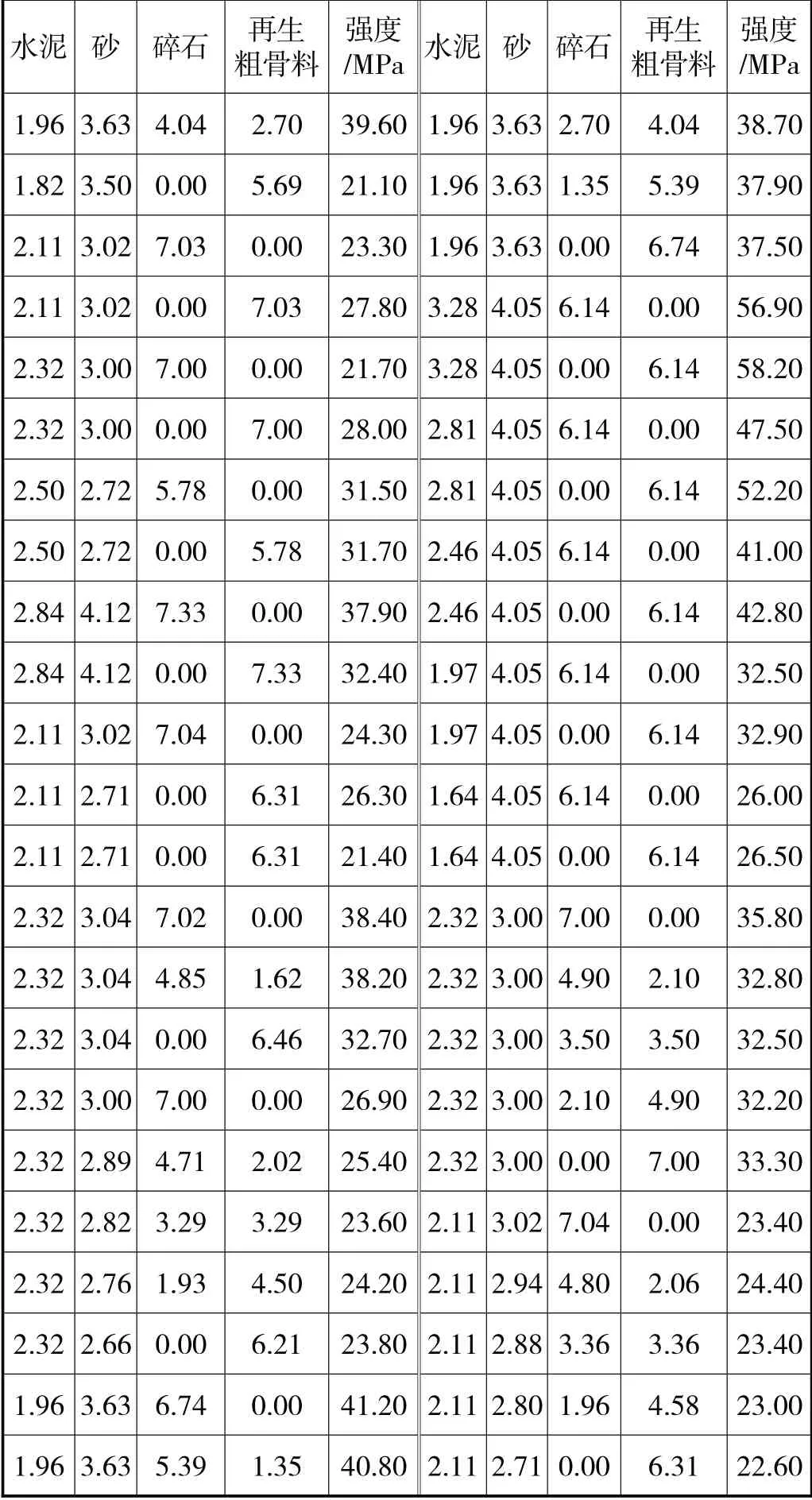
表1 再生混凝土各成分比例与实际强度数据

3 预测模型计算结果对比分析

通过Matlab和Python分别求解神经网络模型和回归模型，各种模型计算结果如表2、图1和图2所示。从表2、图1和图2可知，神经网络模型在解决混凝土强度预测的非线性问题上表现优异，R方为0.97，模型拟合优度最高，但是神经网络模型一直存在可解释性差的问题，这也是阻碍其普遍推广的重要原因。

图2 基于BP神经网络的强度预测

比较而言，一些具体的线性模型和非线性模型一直被广泛应用，表2所示贝叶斯回归模型相对最小二乘回归模型具有更好的拟合优度，并且二者的R方均大于0.85。同时可以发现，贝叶斯线性回归模型更适用于再生混凝土强度的预测；混凝土设计强度的保证率一般不宜低于95%；从图1可知，贝叶斯回归模型和最小二乘回归模型的预测值大都在95%的置信区间内，因此模型具有良好的鲁棒性，可用于中低强度混凝土配合比设计的预测；贝叶斯线性回归模型的R方最大为0.90，因此建议优先使用贝叶斯线性回归模型确定再生混凝土的配合比。

表2 各种预测模型计算结果

由图1可知，混凝土强度等级为C30~C40时，贝叶斯线性回归模型的表现效果较差，部分预测值超出95%的置信区间范围；当混凝土强度等级为C50~C60时，再生混凝土强度预测值均满足95%的保证率的设计要求，因此在低强度混凝土配合比设计时，可以同时以四种模型作为参考依据。

图1 基于最小二乘和贝叶斯参数估计的强度预测

4 结束语

针对再生混凝土强度预测中主客观因素不确定性的影响，利用贝叶斯理论建立再生混凝土强度预测模型，并与最小二乘回归模型和神经网络模型进行对比，分析模型的优势，重点分析其鲁棒性与自适应性，得出以下结论：

（1）贝叶斯线性回归模型在预测再生混凝土强度时，R方为0.90，预测值满足混凝土设计强度95%的保证率要求；相对于低强度再生混凝土，贝叶斯线性回归模型更适合作为中等强度混凝土的配合比设计的参考依据。

（2）相较BP神经网络模型，贝叶斯回归模型和最小二乘回归模型具有更好的可解释性和鲁棒性，二者的R方均大于0.85，符合混凝土实际设计要求。

（3）由于样本量较少，贝叶斯回归模型与最小二乘回归模型的R方相差仅为0.1至0.3，整体效果大致相当。