基于深度展开的大规模MIMO 系统CSI 反馈算法

廖勇，程港，李玉杰

（重庆大学微电子与通信工程学院，重庆 400044）

0 引言

大规模多输入多输出（MIMO,multiple input multiple output）技术凭借其高能量效率、高频谱效率和大系统容量等优势成为下一代移动通信的关键技术之一[1]。为了充分利用大规模MIMO 技术带来的潜在性能增益，基站需要获取足够精确的下行链路信道状态信息（CSI,channel state information）[2]。在时分双工（TDD,time division duplex）大规模MIMO 系统中，可以利用上下行信道的互易性来获得CSI。但是在频分双工（FDD,frequency division duplexing）大规模MIMO 系统中，用户必须先估计下行链路CSI，再通过上行链路反馈回基站[3]。由于大规模MIMO CSI 矩阵具备角度时延域稀疏特性，压缩感知[4]可以被应用于CSI 反馈。虽然压缩感知理论与大规模MIMO 的CSI 反馈模型比较贴合，但目前依然存在一些技术挑战，因此研究人员开始关注深度学习在CSI 领域的应用。文献[5]提出了第一个FDD 大规模MIMO 的CSI 反馈网络CsiNet，它是一种通过引入自编码器结构[6]，并且模拟压缩感知框架构建的高反馈精度的网络，相比于传统的压缩感知方法，有较好的反馈性能和更低的复杂度。为了进一步提升网络的恢复效果，文献[7]在CsiNet 的基础上提出了CsiNet+，该网络在用户设备处利用更大卷积核的卷积层增加CSI 矩阵的感受野，提取更多的深层次特征，在基站处利用更多的卷积网络提高CSI 重构精度。针对快时变FDD大规模MIMO 系统中因多普勒频移导致的信道时间相关性使系统无法保证高可靠和低时延通信的问题，文献[8]利用卷积神经网络（CNN,convolutional neural network）和批标准化网络对CSI 矩阵中的噪声进行提取并且学习信道的空间结构，通过注意力机制提取CSI 矩阵间的时间相关性以提高CSI 重构的精度。在高速移动环境下，信道特征复杂多变，同时存在加性噪声和非线性效应的影响，文献[9]提出一种残差混合网络，可消除高速移动场景加性噪声的影响，学习并适应稀疏、双选衰落信道特征，在高压缩率与低信噪比条件下依然具有较好的性能表现。针对FDD 模式下CSI 反馈方法复杂度高、精度低和开销大的问题，文献[10]提出了一种轻量化低复杂度的反馈方法，该方法在时间复杂度和空间复杂度上均有良好的表现。

值得注意的是，大多数的深度学习方法需要依靠大量已分类标记的数据来进行神经网络的训练，因此这种方法也被称为基于数据驱动的深度学习方法，但该方法不具备可解释性。针对上述问题，研究人员发现将传统的经典非线性迭代算法与深度学习的网络参数训练相结合，可以减小对大量标记数据的强依赖性，同时具备一定的理论保障和性能下限。这种通过结合经典非线性迭代算法的可解释性和深度学习高性能的方法被称作“深度展开”[11]。文献[12]提出一种多任务神经网络结构，通过展开基于最小均方误差准则的两次迭代来恢复下行链路的CSI 和上行用户的数据序列，在减少上行链路带宽资源占用方面表现优异。文献[13]提出基于深度卷积神经网络的马尔可夫模型对前向CSI 进行差分编码，能有效提高CSI 重构精度。文献[14]将快速迭代收缩阈值算法（FISTA,fast iterative shrinkage thresholding algorithm）展开为FISTA-Net 并且作为大规模MIMO的CSI反馈算法，获得了优异的性能。

针对基于深度学习的CSI 反馈算法存在待训练参数过多、可解释性不强的问题，本文提出了2 种基于深度展开的CSI 反馈算法，以近似消息传递（AMP,approximate message passing）[15]作为深度展开的基准算法，从2 个视角分别展开得到了基于可学习参数的 AMP（LP-AMP,learnable parameters-AMP）算法和基于卷积网络的AMP（CNN-AMP,convolutional neural network-AMP）算法。本文的主要贡献如下：1) LP-AMP 算法通过改进AMP 中的阈值函数和Onsager 项来解决CSI 矩阵非严格稀疏的问题；2) 随着这种非严格稀疏性的加强，在LP-AMP 算法的基础上提出了利用卷积残差学习网络改进阈值函数模块的 CNN-AMP 算法，与LP-AMP 相比，CNN-AMP 在牺牲了一些复杂度的情况下，获得了更加明显的重构效果；3) 所提的基于深度展开的CSI 反馈算法既具有压缩感知算法的可解释性理论保障，又具有深度学习方法的高性能表现，可以为FDD 大规模MIMO CSI 反馈领域的研究提供一些可行的思路。

1 系统模型

本文针对单小区大规模MIMO 的通信系统，基站配备有Nt根发射天线，天线阵列方式采用均匀线性阵列，用户端配备有单根接收天线。采用正交频分复用系统，并有Ns个子载波，因此接收向量y可以建模为

其中，y是维度为Ns×1 的复数接收向量；x是Ns×1的复数发射向量；n是Ns×1的加性高斯白噪声向量；是Ns×Nt的复数CSI 信道矩阵，其中行向量为每个子载波下的空域信道矢量，列向量为频域信道矢量；U是Nt×Ns的复数预编码矩阵。如果以空频域矩阵作为反馈矩阵的基准，那么CSI 矩阵就是，此时的反馈总量是NsNt，这会占据大量的系统资源，因此需要设计低复杂度高反馈精度的有限CSI 反馈方法。

考虑到CSI 矩阵具备角度时延域的稀疏特性，为了降低CSI 的反馈开销，将角度和时延域的稀疏特性全部应用于空频域矩阵，经过两次矩阵乘积的离散傅里叶变换（DFT,discrete Fourier transform），即可得到角度时延域稀疏CSI 矩阵为

将上述经DFT 稀疏和截断之后的CSI 矩阵H作为待反馈矩阵，深度展开CSI 反馈模型如图1 所示。首先，将用户端估计得到的CSI 矩阵H经向量化和拼接得到长度为N=的实数稀疏向量x，在得到稀疏的待反馈向量x之后，测量矩阵使用独立同分布高斯随机矩阵A进行压缩。将矩阵的压缩和重构2 个过程分别使用编码器和解码器进行描述，编码器在用户设备处，解码器在基站处。编码过程表示为

图1 深度展开CSI 反馈模型

其中，y表示长度为M的测量向量，fen(·) 表示编码器函数，Re(·) 表示取向量的实部，Im(·) 表示取向量的虚部，vec(·) 表示向量化操作。

y通过反馈信道到达基站，为了便于区分，以表示基站端接收到的测量向量，基站通过深度展开的AMP 算法恢复为第k次迭代的重构向量xk，然后反变换回CSI 稀疏矩阵，即可完成CSI 的反馈流程。解码过程表示为

其中，fde(·) 表示解码器函数。最终的训练过程是将fen(·) 和fde(·) 联立在一起进行端到端的训练，这种端到端的训练过程可表示为

其中，fall(·) 是编码器和解码器联立后的变换函数，Θ={Θen,Θde}是网络的参数集合，Θen是编码器参数，Θde是解码器参数，Hi是第i例训练样本。

2 基于AMP 的深度展开CSI 反馈

2.1 深度展开的原理

深度展开模型由多个计算模块组成，每个计算模块对应非线性迭代算法中的一次迭代。文献[16]指出，将深度学习方法与现有通信领域中的经典非线性迭代算法结合已成为近年来的研究热点，并且已经应用到预编码、信号检测和信道解码等处理中。深度展开模型架构如图2 所示。

图2 深度展开模型架构

深度展开模型包括3 个部分，即数学模型、迭代算法和深度网络。在应用中将具体的实际问题抽象为数学模型，根据相关的数学理论推导得到具体的迭代算法，将迭代算法每轮迭代的计算式展开为深度网络中的一层，利用可学习参数或神经网络替换原始迭代算法中每轮迭代中的超参数或某个计算模块。

2.2 AMP 算法

AMP 算法[15]很好地继承了迭代阈值算法的优势，又融入了消息传递算法的精髓。假设初始化重构向量x0=ATy，残差向量z-1=y，第t（t≥ 0）次迭代可表示为

其中，u为软阈值函数的输入。

根据文献[17]，Onsager 校正项中的bt与阈值λt为

其中，ε是一个与稀疏度和测量向量长度M有关的可调数值。AMP 算法与FISTA 相似，不同之处在于AMP 算法在残差向量更新时增加了Onsager 校正项，并且迭代阈值在每轮迭代中都会通过残差向量和测量向量长度M进行调整。AMP 计算模块如图3 所示。

图3 AMP 计算模块

图3 展示了AMP 算法迭代式中的每一个计算模块，AMP 算法的流程如算法1 所示。

算法1AMP 算法

输入测量向量y，高斯随机矩阵A

输出重构向量xt+1

初始化重构向量x0=ATy，残差向量z-1=y，迭代次数t=1

步骤3t=t+1，若t＜N，返回步骤1，若t=N，迭代结束；

2.3 基于可学习参数的AMP 算法

本节对基于可学习参数的 AMP 反馈算法LP-AMP 的展开结构进行描述。具体而言，通过引入深度学习中梯度下降法更新网络参数，优化AMP算法中的迭代更新参数，将算法的每轮迭代展开为深度网络中的一层，再将多个这样的层堆叠，在模型训练的过程中逐渐优化每层中不同的可学习参数，使模型以更少的迭代层数更快地收敛。LP-AMP的中间展开计算模块如图4 所示。

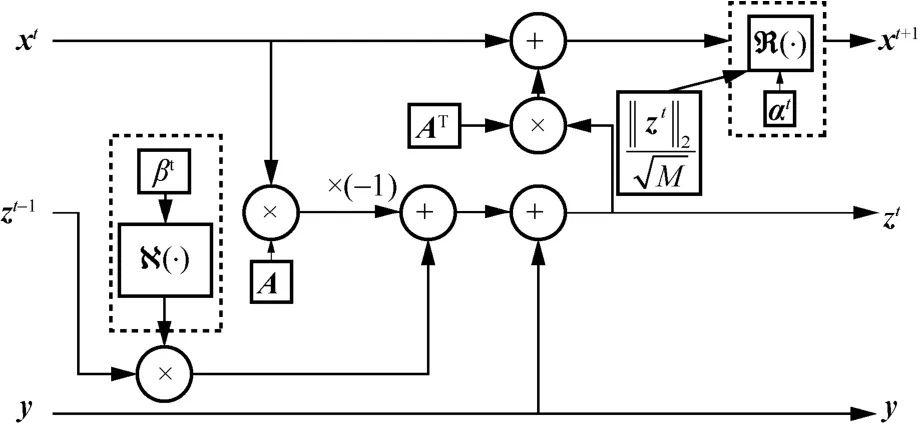
图4 LP-AMP 的中间展开计算模块

输入层对进入迭代中的x t和z t进行初始化操作，输出层将迭代至最后的x k作为LP-AMP 的最后输出，中间展开计算模块的 R(·) 和 N(·) 函数是引入可学习参数α t向量和β t参数的2 个可学习模块。LP-AMP 算法的初始化和中间展开式可以表示为

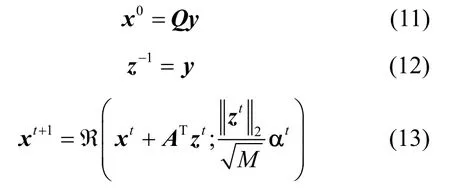
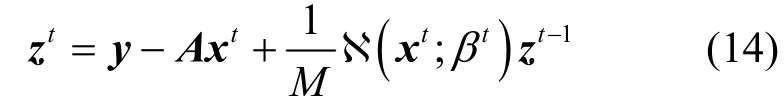
其中，x0的初始化是通过将采样矩阵的转置AT作为可学习矩阵Q的初始化，在不断训练的过程中，调整矩阵Q的分布，增强初始重构效果；α t是第t层展开中的可学习向量；β t是第t层展开中的可学习参数。对于展开式中的 R(·) 和 N(·) 模块，R(·) 模块对应原始AMP 算法中的阈值函数η(·) 部分，与阈值函数有所不同；N(·) 模块则对应于Onsager 项部分中的对x t的0 范数计算过程。

阈值函数η(·) 和 R(·) 模块的对比如图5 所示。

图5 阈值函数 η (·) 和 R(·) 模块的对比

从图5 可以看出，原始的CSI 数据并非严格稀疏，大多数的数据非常接近0，但是并不为0。阈值函数η(·) 则在一次更新迭代的情况下将绝对值小于阈值λt的参数严格置0，这破坏了原始信号的细节（即小于阈值但不为0 的点在重构信号中被删除）。本文将原始的阈值函数η(·) 替换成 R(·) 计算模块，是为了加强阈值函数在应对非严格稀疏数据时的非线性表征能力。与η(·) 阈值函数不同的是，R (·) 模块引入可学习向量αt来提升整体的变换效果，计算式为

其中，α t∈RN是长度为N的可学习参数向量，它的长度与重构向量x t的长度相同，即N=。R(·) 模块的计算式使不会有小于阈值的点被严格置0，并且每个数据点都有一个可学习参数进行调整。

N(·) 模块对应于AMP 算法中Onsager 中求解x t的0 范数部分，x t的0 范数是指向量x t中的非零元素的数目。但是通过 R(·) 模块处理后的数据几乎不存在严格为0 的数据，因此 N(·) 模块中对0 范数的处理同样需要通过可学习参数来模拟。具体而言，将可学习参数βt作为计算非零元素数目的阈值，超过βt阈值的数据点被判定为非零元素。通过后续的仿真实验可以看到，引入可学习参数βt可以减少算法的总迭代次数并提高重构精度。另外，值得注意的是，采样矩阵A是服从高斯分布的随机矩阵。然而，已有研究证明，设计合理的采样矩阵可以提高CSI 矩阵重构的精度[18]。在LP-AMP 中也不例外，为了提高重构精度，利用经训练过后的A进行数据的压缩，Q进行数据的初始重构。LP-AMP算法的流程如算法2 所示。

算法2LP-AMP 算法

输入测量向量y，训练后的矩阵A

输出重构向量xt+1

初始化重构向量x0=Qy，训练后的矩阵Q的初始化为AT，残差向量z-1=y，迭代次数t=1

步骤1由测量向量y、训练后的矩阵A、当次迭代的xt、当前展开计算模块中的可学习参数β t、前一次迭代的z t-1计算出当次迭代的z t=y-Ax t+M-1N（x t;βt）z t-1；

步骤2引入可学习参数αt向量，利用当前展开计算模块中的R(·) 计算得到

步骤3t=t+1，若t＜N，返回步骤1，若t=N，迭代结束；

2.4 基于卷积网络的AMP 算法

LP-AMP 的 R(·) 阈值模块依然面临一个重要的问题，即虽然LP-AMP 通过可学习参数作为每层的阈值向量，但是在训练之后会使 R(·) 模块中的阈值向量α t成为固定值，这会使个别不符合总体样本特征的数据重构效果变差，进而影响算法的整体泛化能力。在LP-AMP 的整个流程中，R(·) 模块几乎承担着大部分的非线性计算过程，而深度学习中CNN在应对非线性表征时，往往有着更好的性能。因此本节利用卷积残差学习模块替换LP-AMP中的阈值模块 R(·)，其余部分不做任何改动。为了方便后续的描述，将基于卷积残差学习网络的AMP 反馈算法命名为 CNN-AMP。从理论推导角度而言，LP-AMP 中 R(·) 的作用是去除数据中的高斯白噪声影响。具体的推导过程如下。

根据y=Ax可得

根据上述推导，AMP 算法中η(·) 阈值函数的作用是去除每轮迭代重构信号中的高斯白噪声。CNN-AMP 的中间展开计算模块如图6 所示，其与LP-AMP 的不同之处仅在于将 R(·) 模块替换为了℘(·) 模块，℘(·) 模块由3 个深度可分离卷积层[19]构成，卷积核的大小为3×3，每个卷积层之间通过ReLU 激活函数相连。值得强调的是，℘(·) 模块利用残差学习[20]的模式，将网络的输入减去网络的输出得到最终结果，即 ℘(·) 模块将学习到每轮重构向量的高斯白噪声，最后通过输入减去噪声得到该展开层信号的重构。

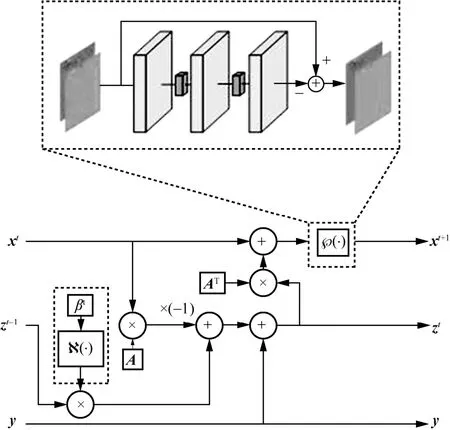
图6 CNN-AMP 的中间展开计算模块

根据上述对CNN-AMP 的描述，它的迭代展开式可以写为

其中，CNN-AMP 中的 (Nxt;βt) 模块与LP-AMP保持一致，依然利用学习参数 βt作为模拟求解xt的0 范数阈值。CNN-AMP 的输入层的初始化过程以及输出层也与LP-AMP 保持一致，为了提高重构精度，采样矩阵A与初始重构矩阵Q同样加入网络参数的训练。CNN-AMP 算法的流程如算法3 所示。

算法3CNN-AMP 算法

输入测量向量y，训练后的矩阵A

输出重构向量xt+1

初始化重构向量x0=Qy，训练后的矩阵Q的初始化为AT，残差向量z-1=y，迭代次数t=1

步骤1由测量向量y、训练后的矩阵A、当次迭代的x t、当前展开计算模块中的可学习参数β t、前一次迭代的z t-1计算出当次迭代的z t=y-Axt+M-1N(x t;βt)z t-1；

步骤2引入残差学习模块 ℘(·)，利用当前展开计算模块中的 ℘(·) 计算得到x t+1=℘(x t+ATz t)；

步骤3t=t+1，若t＜N，返回步骤1，若t=N，迭代结束；

3 模型训练与复杂度分析

3.1 模型训练

对比LP-AMP、CNN-AMP 和AMP 的展开或迭代式可以发现，若去掉LP-AMP 和CNN-AMP中的 R(·)、N (·) 和 ℘(·) 模块，将其更改为原始阈值函数η(·) 和常规的 0 范数计算，LP-AMP 和CNN-AMP 就会退化为AMP 算法，也就是说，LP-AMP 和CNN-AMP 的性能下限是可以预知的，即存在理论前提和性能保障。但是基于数据驱动的深度学习方法的性能则无法提前预知，在进行训练之前，无法保证得到很好的效果。为了方便后续对比实验的分析，这里k1层展开的LP-AMP和k2层展开的CNN-AMP 被命名为LP-AMP-k1和CNN-AMP-k2。产生数据集的信道模型是基于空间几何的随机信道模型 COST2100[21]，其在COST259 模型和COST273 模型的基础上进行构建，可以在时间、频率和空间上重现MIMO 信道的随机属性。产生的数据集分别为100 000 训练集、30 000 验证集和20 000 测试集。采用端到端的训练方式，训练的损失函数采用均方误差（MSE,mean square error），它是一种计算预测值和真实值之间误差的函数，具体的表达式为

其中，Hi为原始输入的第i例样本，矩阵的维度是32×32，Θ为网络中的所有参数，包括A、Q、α t、β t等，fall(·) 为整个网络的计算式，fall(Hi;Θ)为恢复的第i例样本，T为总的训练样本数量。优化器算法为自适应矩估计[22]优化器，它是随机梯度下降算法的一种变体。采样矩阵A使用服从高斯分布的随机矩阵初始化填充，第t层可训练向量α t使用0.1 初始化填充，第t层β t也初始化为0.1。

为了得到理想效果并避免梯度消失的问题，初始学习率设置为0.001，衰减率设置为0.9。使用的训练设备配置为NVIDIA GeForce RTX 2080 Ti 显卡，Intel Xeon E5-2678 v3 处理器，64 GB 内存。通过实验发现，LP-AMP-k1的收敛速度比CNN-AMP-k2快得多。当压缩率，批量数据大小为200，k1和k2分别取3 和7 时，LP-AMP-k1和CNN-AMP-k2的MSE 如表1 所示，采用Python平台的深度学习框架Pytorch 搭建整体结构。

表1 LP-AMP-k1 和CNN-AMP-k2 的MSE

除此之外，还需要确定AMP 算法的收敛迭代次数，及LP-AMP-k1和CNN-AMP-k2的最佳展开层数。当室内场景下压缩率时，LP-AMP-k1和CNN-AMP-k2在验证集上的MSE如图7 所示。从图7 可以看出，当k1=1、3、5、7、9 时，LP-AMP-k1整体损失呈下降趋势，但是损失整体相差并不大，随着k1的增大，最终收敛的迭代次数开始增加，k1=3 和k1=5 时的收敛速度几乎相同，k1=5 时的整体损失仅略低于k1=3。综合复杂度和性能平衡之下，设置k1=3。另外，CNN-AMP-k2整体的损失比LP-AMP-k1低一个数量级，这也是在牺牲一些复杂度之下换取的性能优势。随着层数的增加，CNN-AMP-k2损失同样呈下降趋势，k2=5 和k2=7 时的损失差距不大，为了平衡复杂度和性能，设置k2=5。

图7 LP-AMP-k1 和CNN-AMP-k2 在验证集上的MSE

AMP 的迭代次数q也是影响整体复杂度的关键参数，MSE 随迭代次数的变化如图8 所示。无论在室内或室外场景，AMP 算法信道矩阵的非严格稀疏性导致算法在验证集上整体收敛于迭代次数50～100，以下的计算选取q=100。相比于LP-AMP-3，AMP 的乘法次数高一个数量级，与CNN-AMP-5较接近。

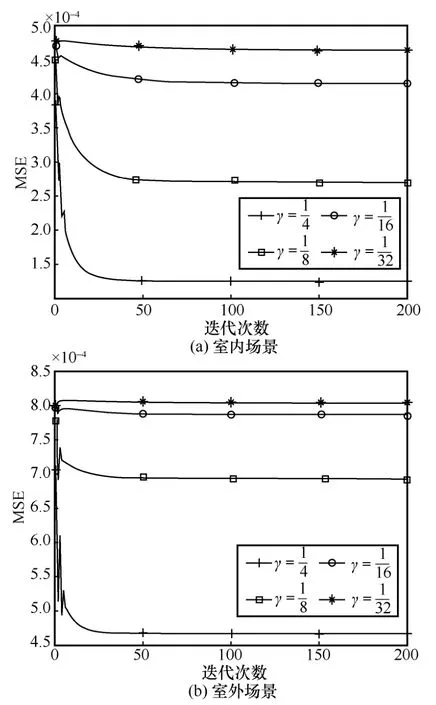
图8 MSE 随迭代次数的变化

3.2 复杂度分析

本节将通过对比 CsiNet、CsiNetPlus、LP-AMP-3、CNN-AMP-5 和AMP 方法来说明深度展开方法的优势和缺陷，通过分析网络的参数量和实数乘法次数来反映复杂度。对于网络参数，AMP作为传统的压缩感知算法并不存在网络参数，但是LP-AMP-3 和CNN-AMP-5 是AMP 的深度展开算法，引入了可学习参数和残差学习模块，需要计算整体的参数量。

参数量的计算将M=512、256、128、64 和N=2048代入计算，并且忽略所有结构的偏置项。不同算法编码器和解码器的参数量如表2 所示。

表2 不同算法编码器和解码器的参数量

LP-AMP-3 和CNN-AMP-5 算法编码器部分的参数量与CsiNet 和CsiNetPlus 几乎相同，这是因为LP-AMP-3 和CNN-AMP-5 都将采样矩阵A作为可训练参数，这与全连接神经网络的压缩过程在参数量的计算上是等价的。

在解码器部分，LP-AMP-3 和CNN-AMP-5 比CsiNet 和CsiNetPlus 的参数量略大，不过总体来说，M×N依然是参数量计算的主体部分，数量级依然相同。LP-AMP-3 存在可训练矩阵Q以及 R(·)、N (·) 模块中的向量α t和参数β t，CNN-AMP-5 与LP-AMP-3 同样存在可训练矩阵Q，不同之处在于，R(·) 模块被替换为 ℘(·) 模块，当层数越大时，参数量相应也就越大。

不同算法的乘法次数如表3 所示。AMP、LP-AMP-3 和CNN-AMP-5 在编码器部分的乘法次数一样，这是因为在压缩感知算法的框架中，编码器部分都是采样矩阵A与待压缩向量x的乘积，而所提算法和CsiNet 和CsiNetPlus 的乘法次数几乎相同，这是因为它们的计算量主要来源于M×N。在解码器部分，LP-AMP-3 在压缩率为时比CsiNet 和CsiNetPlus 的乘法次数多，在其他压缩率时则相反，这是因为所提算法的计算量不仅与展开层数有关，并且受M×N的影响较大。不管在哪种压缩率下，CNN-AMP-5 的乘法次数都高于 CsiNet 和CsiNetPlus，这主要是受 ℘(·) 模块的影响。和AMP算法相比，LP-AMP-3 和CNN-AMP-5 的复杂度较低，这是因为它们的展开层数远小于AMP 的总迭代次数 100。另外，CNN-AMP-5 的复杂度比LP-AMP-3 高，原因在于 ℘(·) 模块使用了连续的卷积层。

表3 不同算法的乘法次数

4 仿真分析

本节将对比 LP-AMP-3、CNN-AMP-5、CsiNet、CsiNetPlus 和AMP 算法的CSI 反馈性能。经两次DFT 得到角度时延域矩阵H，保留该矩阵的前=32 行，因此复数矩阵H的维度为32×32，再将复数矩阵改为实虚部双通道矩阵。压缩率，M=512、256、128、64，N=2 048。在MATLAB 平台进行仿真，设备配置与第3 节相同，仿真系统主要参数如表4 所示，其他参数都遵循文献[21]中的默认设置。

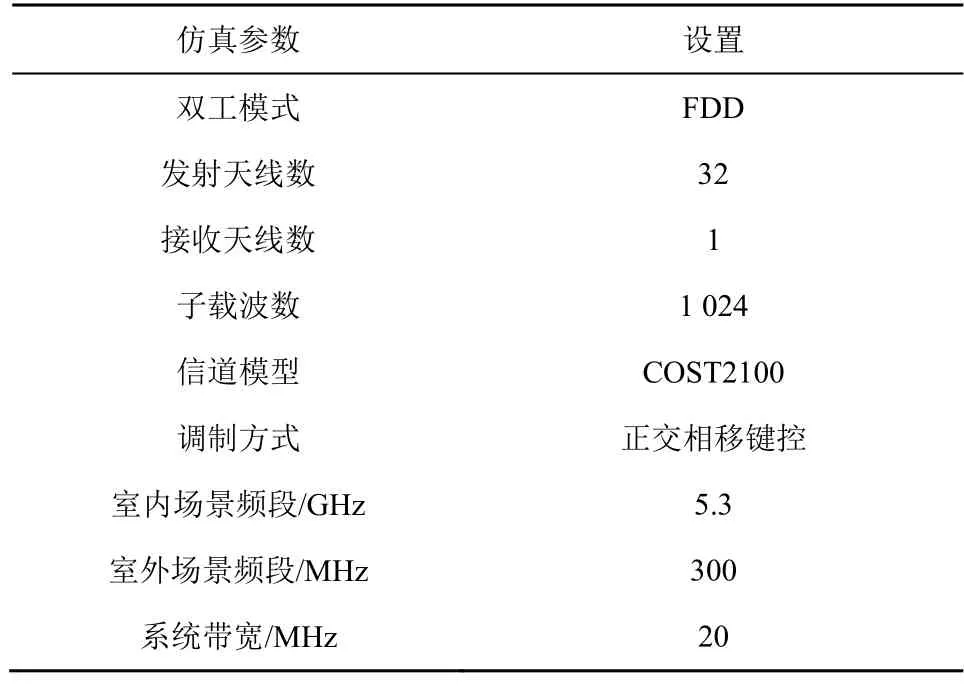
表4 仿真系统主要参数

4.1 归一化均方误差

将离线训练好的模型应用于室内室外场景下的测试集，并通过计算原始矩阵与重构矩阵之间的归一化均方误差（NMSE,normalized mean squared error）对模型的性能进行量化评估。NMSE的计算式为

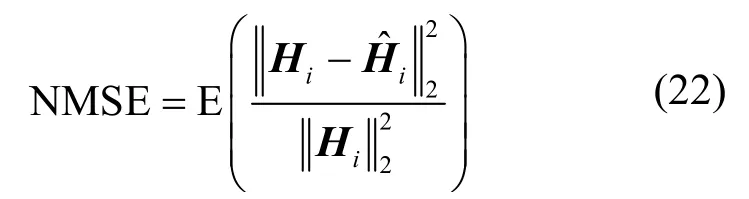
其中，Hi和分别表示原始信道数据和恢复信道数据。不同方法在室内和室外场景下的NMSE如图9 所示。

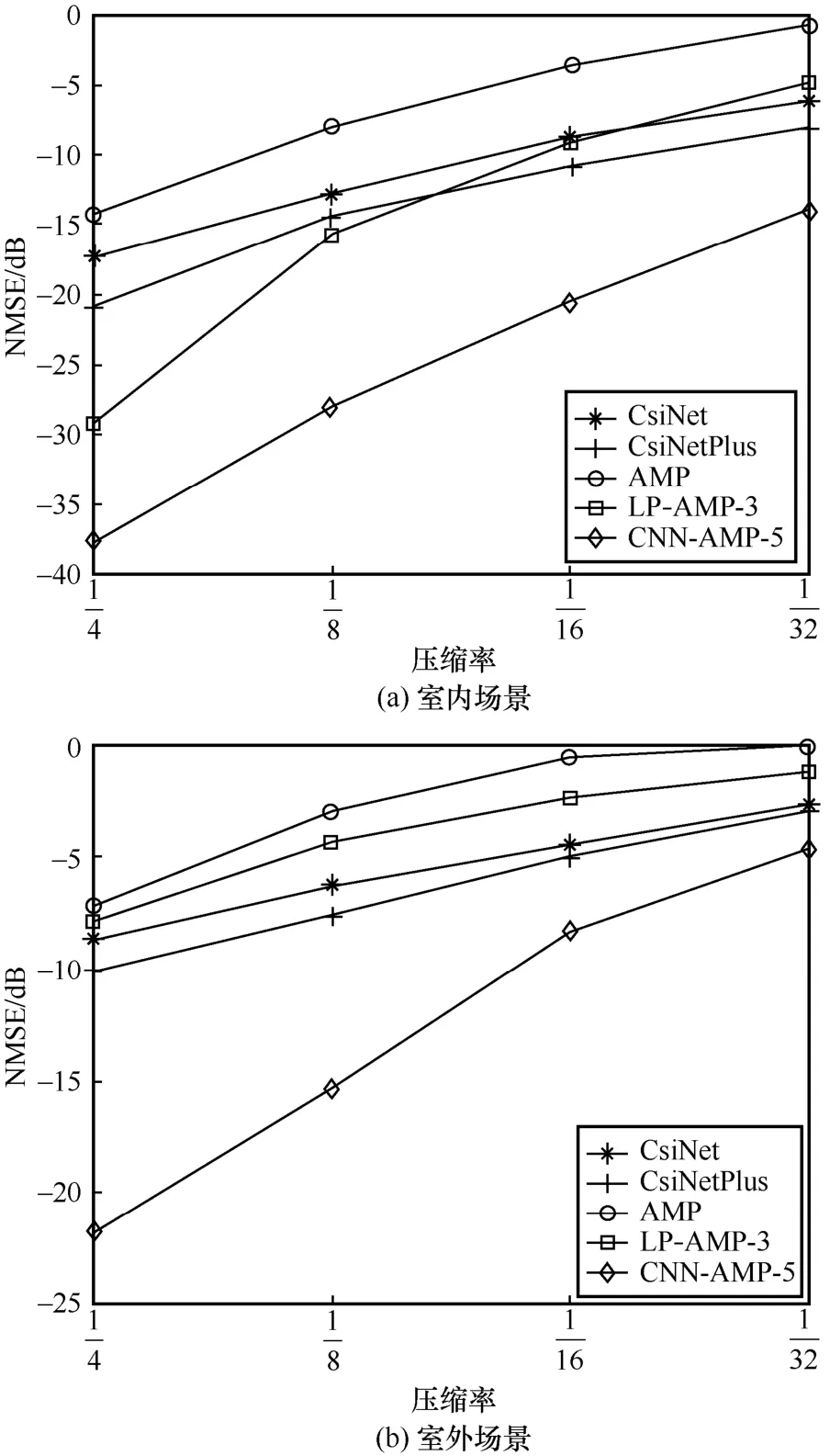
图9 不同方法在室内和室外场景下的NMSE

4.2 相似度

除NMSE 之外，余弦相似度ρ同样可以用来对比不同算法之间CSI 矩阵的重构精度。该指标可以体现重构的CSI 矩阵与原始CSI 矩阵之间的相似程度，其计算式为

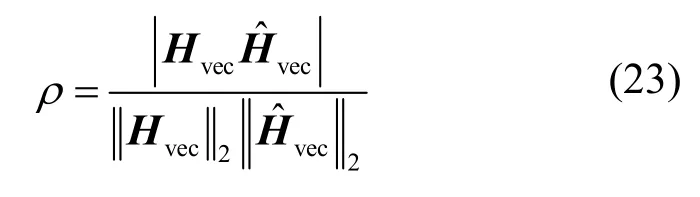
其中，Hvec、分别表示向量化后的CSI 信道矩阵和重构的CSI 信道矩阵，ρ值越大，说明两者越相似，重构精度越高。不同方法在室内和室外场景下的余弦相似度如图10 所示。

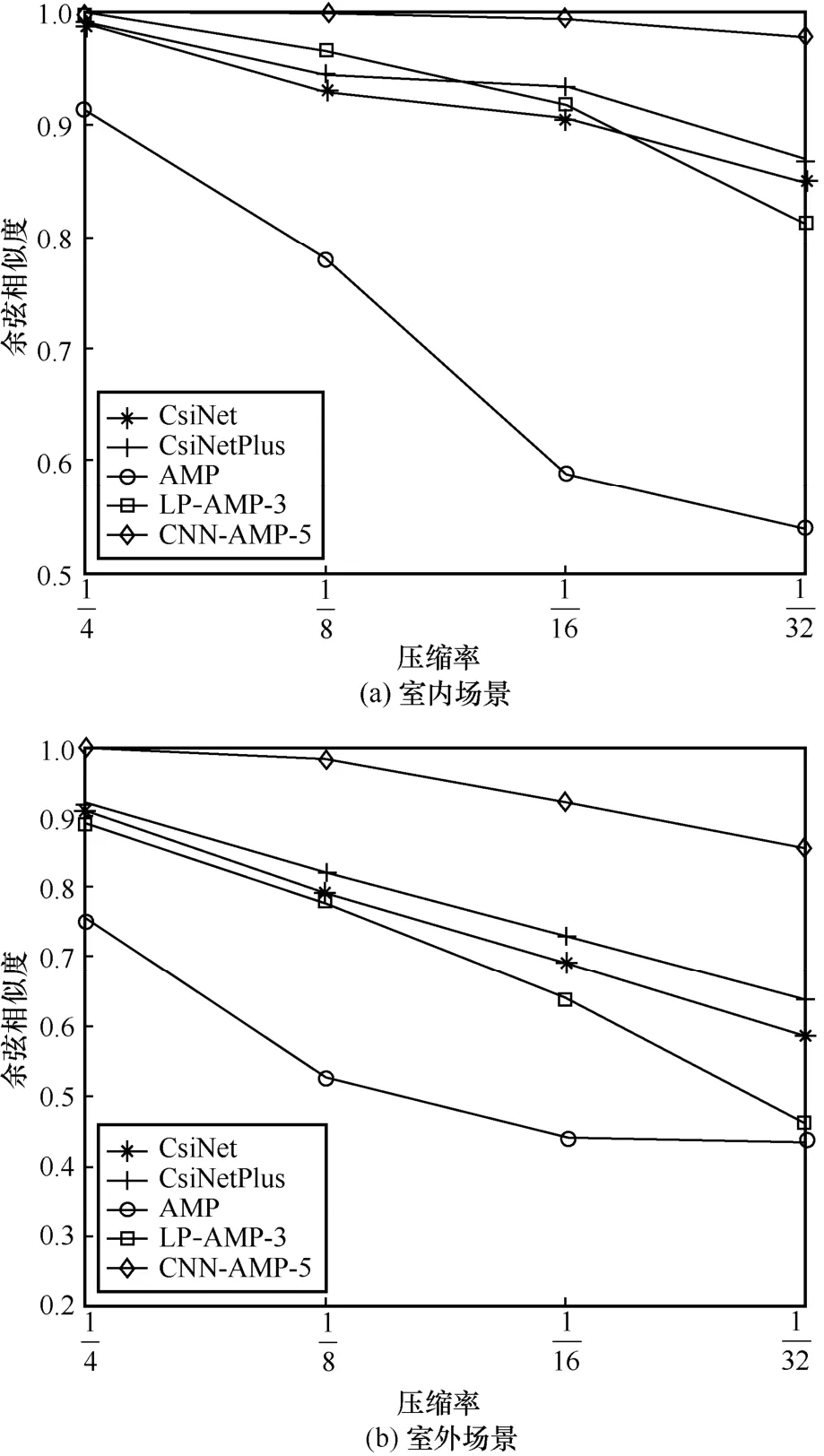
图10 不同方法在室内和室外场景下的余弦相似度

由图10 可知，经典压缩感知的AMP 算法在不同场景、不同压缩率下的ρ均低于其他几种算法，即CSI矩阵的重构相似度均低于其他算法。在室内场景下，AMP 算法在压缩率为时ρ明显下降，而在室外场景下，AMP 在各压缩率下的ρ都不够理想，已无法满足大规模MIMO 系统CSI 反馈的精度要求。LP-AMP-3 算法在室内场景的不同压缩率下的ρ与CsiNet 和CsiNetPlus 算法比较接近，在室外场景的不同压缩率下的ρ略低于CsiNet 和CsiNetPlus 算法。CNN-AMP-5 算法不仅在室内场景的不同压缩率下保持较高的ρ，在室外场景下也有着优异的表现，可以满足大规模MIMO 系统CSI 反馈的精度要求。

5 结束语

本文研究了基于深度展开的大规模 MIMO CSI 反馈算法。在AMP 算法迭代过程的基础上，从2 个角度将其深度展开，提出了基于可学习参数的AMP 深度展开算法LP-AMP 和基于卷积残差学习模块的AMP 深度展开算法CNN-AMP。针对信道矩阵的非严格稀疏性的问题，LP-AMP 通过深度学习的方法改进了阈值函数，增强了AMP 算法应对室内场景的性能，降低了算法的复杂度。在室外场景下，随着信道矩阵的剧烈变化，非严格稀疏性问题逐渐增大，针对这个问题，本文又提出CNN-AMP 算法，将LP-AMP 算法中改进的阈值函数模块替换为卷积残差学习模块，该模块可以消除AMP 算法在每次迭代更新后重构向量中的高斯随机噪声。因此无论是在室内场景下还是在室外场景下，与代表性算法相比，所提算法都有明显的优势。本文提出的基于深度展开的CSI 反馈算法既具有压缩感知算法的可解释性理论保障，又具有深度学习方法的高性能表现，可以为大规模MIMO CSI反馈提供一些参考，未来还可以从降低复杂度方面对算法进行改进。