基于模糊证据理论的六氟化硫电气设备绝缘性能评估研究
2023-01-26金綦庆杨正刚张成诚
金綦庆,汪 涛,杨正刚,张成诚,胡 敏
(1.西南油气田公司天然气净化总厂,重庆 400020;2.重庆科技学院电气工程学院,重庆 401331)
0 引言
随着计算机技术、人工智能和测试技术的快速发展和广泛应用,国内外对有关设备状态评估展开了一系列研究。张立功、黄城等用DR检测技术实现了对GIS中设备内部结构的可视化诊断,能对其内部缺陷进行有效地初步诊断[1-2]。王涛云等在GIS中设备状态评估中采用可拓分析理论,对于其状态评估中各指标的权重问题运用熵值法理论得到有效解决[3]。律方成等采用了一种基于超声波传感器的识别方案,其识别率达到了80%左右[4]。赵云峰、陈兢、贺翔、王涛云等将Petri网理论与模糊推理规则有机结合在一起,通过模糊和证据理论对绝缘进行状态评估[5-14];刘勇业等则将特征气体作为模糊Petri网的输入库所,建立GIS中设备绝缘故障诊断模型,利用Petri网分析GIS中设备缺陷类型的置信度[15-16]。在现有的研究工作中,六氟化硫电气设备状态监测的发展方向主要是基于人工智能和神经网络的大规模专家系统[17],而对六氟化硫电气设备进行状态评估的相对较少。因此,加大对六氟化硫电气设备状态评估研究十分重要。
1 实验分析
1.1 特征量的选取
六氟化硫电气设备绝缘状态与气体状态有关,主要包括六氟化硫气体的微水含量、气体的压力(密度)、气体成分等[18],故选择灭弧室微水量、其他气室微水量、气体泄漏率和分解产物作为评价六氟化硫电气设备绝缘性能的4个特征量。
1.2 模糊试验法确定隶属度
针对六氟化硫电气设备绝缘性能4个特征量确定其隶属度时采用模糊统计试验的方法。邀请28位专家填写如表1所示的调查表,以确定各特征量隶属度,从而得到单因素评判矩阵。

表1 六氟化硫电气设备灭弧室微水含量对应的状态单位:μL/L
六氟化硫电气设备的4个特征量越小越优,故选择式(1)作为归一化函数

其中,f(x)为隶属函数自变量;x为参量原始数据;b为规程中规定的阈值。
根据国家电网公司变电检测管理规定:有电弧分解物隔室的运行中微水含量要求不大于300μL/L,无电弧分解物隔室的微水含量不超过500μL/L,气体泄漏率不超过1%,分解产物不超过10μL/L,由此可知各特征量阈值。
由式(1)可以得到表1相应的归一化值,其他气室微水量、气体泄漏率和分解产物类似。
1.3 特征类型的选取
六氟化硫电气设备绝缘状态界限不是特别明显,因此对六氟化硫电气设备的不同绝缘状态进行描述时可用信息熵。信息熵是描述系统混乱的程度,熵值越高系统越混乱。不同方面的有序程度可以用不同的熵进行描述。可以将系统信息熵定义为:设W是一个可测集合类v生成的代数和,具有p测度,p(W)=1的勒贝格空间,且其有限划分C={Ci}中互不相容集合的形式可以用W表示,即

本文通过采用小波能量谱熵、功率谱熵、奇异谱熵、小波空间状态特征谱熵的特征来描述六氟化硫电气设备的绝缘状态。
1.4 隶属度函数类型的确定
由于六氟化硫电气设备不同绝缘情况下,同一熵特征均服从高斯分布,因此隶属度函数可选择高斯型,即

其中,a、b分别为期望和均方差,为了得到隶属度函数矩阵,采用样本参数估计的方法。
表2—表5为六氟化硫电气设备特征量功率谱熵对应的a、b值。

表2 小波能量谱熵在不同情况下的期望和均方差

表3 功率谱熵在不同情况下的期望和均方差

表4 奇异谱熵在不同情况下的期望和均方差

表5 小波空间状态特征熵在不同情况下的期望和均方差
2 绝缘状态判别
首先,对4个特征量的样本数据提取4种熵特征,确定出隶属度函数的参数,再融合不同特征量的数。例如,提取某六氟化硫电气设备各绝缘状态下的微水量,得到该样本小波能量谱、功率谱、奇异谱和小波空间谱,然后代入式(4)可得到各绝缘状态隶属度值:

各熵值之间相互支持的程度通过隶属度间偏差大小来衡量,定义dij越大两不同熵值之间的支持度就越低,dij越小两不同熵值之间的支持度就越高。因此,同一特征量不同算法的融合度函数可定义为

为了保证达到最大的可信度,确定第i个熵值其他熵值的相融度时,可取与第i个特征熵值相融度中最小的其他熵值,即得到:
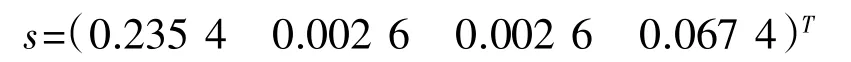
设第i个特征量的权系数可由si在总相融度中所占的比重确定,即

由此得到权重系数向量为

融合后的灭弧气室微水量属于各绝缘状态的隶属度为
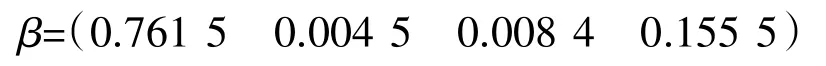
通过上述方法,就完成了某一个特征量的绝缘性能评价的融合,以此类推可得到另外3个特征量绝缘状态判别的结果,然后利用证据理论进行绝缘判别。
同时,由于提取了六氟化硫电气设备绝缘性能的M类特征,基本信任分配函数对应为m1,m2,...,mM,并且每类特征都与相同的K类绝缘状态对应,因此,基本信任分配函数的焦元也相同。
基本信任分配函数的值可由融合后的隶属度值转化得到,为满足∑m(Ai)=1,可由式(7)来确定:
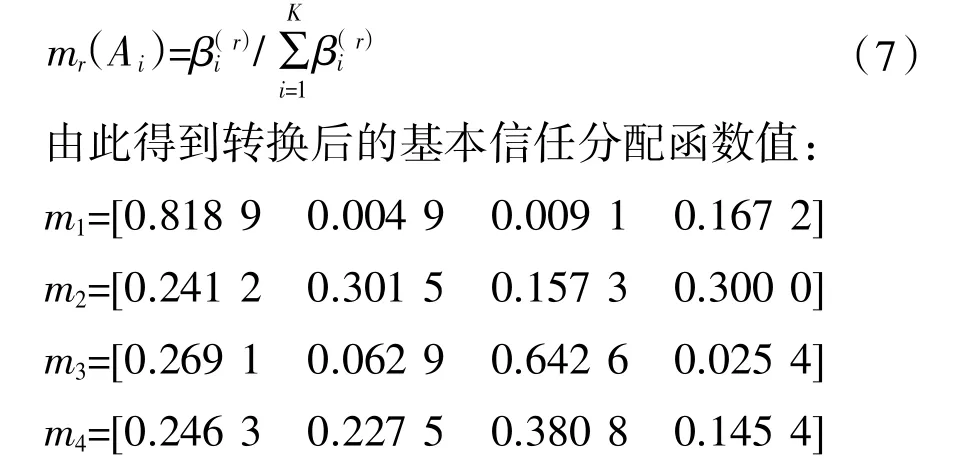
由于存在多类特征,进行两两融合时采用证据理论,即对m1,m2,m3,m4两两融合得到:

根据以上判断,该六氟化硫电气设备绝缘类型为良好,并且与实际情况相符。同时,也可采用同样的方法对于其他样本数据进行识别。篇幅有限不一一列举。
3 结束语
利用连续采样六氟化硫电气设备的4个特征量进行分析判断,通过大量的测试数据,得到相应的评判范本。然后将需要测试的六氟化硫电气设备参数利用该范本进行绝缘能力判别。本文综合考虑各类特征间的相互关系,避免产生融合过程中的主观化,提出了基于模糊证据理论的识别方法,该方法能对各种情况下的六氟化硫电气设备特征进行有效融合,并通过实验证明了该方法的有效性。
