Failure Mode and Effects Analysis Based on Z-Numbers and the Graded Mean Integration Representation
2023-01-25HanhanZhangZhihuiXuHongQianandXiaoyanSu
Hanhan Zhang,Zhihui Xu,Hong Qian and Xiaoyan Su,★
1School of Automation Engineering,Shanghai University of Electric Power,Shanghai,200090,China
2State Key Laboratory of Nuclear Power Safety Monitorig Technology and Equipment,Shenzhen,518172,China
ABSTRACT Failure mode and effects analysis(FMEA)is a widely used safety assessment method in many fields.Z-number was previously applied in FMEA since it can take both possibility and reliability of information into consideration.However,the use of fuzzy weighted mean to integrate Z-valuations may have some drawbacks and is not suitable for some situations.In this paper,an improved method is proposed based on Z-numbers and the graded mean integration representation(GMIR)to deal with the uncertain information in FMEA.First,Z-numbers are constructed based on the evaluations of risk factors O,S,D for each failure mode by different experts.Second,weights of the three risk factors and experts are determined.Third,the integration representations of Z-numbers are obtained by a new method based on the GMIR method.Finally,risk priorities of the failure modes are derived considering the weights of experts and risk factors.Two examples and a case study are given to show the use of the proposed method and comparison with other methods.The results show that the proposed method is more reasonable,universal and simple in calculation.
KEYWORDS Safety assessment;FMEA;risk priority number;Z-number;the graded mean integration representation
1 Introduction
Safety assessment is an important task for large complex systems,such as nuclear power plants[1],aerospace systems[2],metro tunnels[3,4],bridges[5],and gas pipelines[6,7].It includes structure reliability analysis [8,9],component reliability analysis [10,11] and even human reliability analysis[12],and can been conducted by using various methods,both qualitative [13,14] and quantitative[15–17].Failure mode and effects analysis(FMEA)that originated in 1955[18]is a widely used safety assessment method in many industry fields such as aircraft manufacturing,military systems,and engineering designs[19–22].In these fields,there are multiple failure modes with different associated probabilities and consequences.FMEA is a method which aims to aggregate information for risk management decisions.It not only helps people to pick out failure modes by considering the causes and consequences,but also helps people to pick out the key point in designing which requires improvement and special control.
Risk priority number (RPN) which is used to prioritize failure modes in FMEA has been conducted a lot of considerable research by investigators over the years[23–28].The traditional RPN method has been widely used to solve the problem of risk evaluation and maintenance strategy design under limited time and resources in a quantity of industries.However,the use of the traditional RPN in FMEA exposes some drawbacks.
Uncertainty is an important problem in failure analysis in traditional RPN.In order to deal with uncertain information more effectively,fuzzy set theory was first introduced to represent the uncertainty in risk evaluations.It relies on the membership functions and reasons by the if-then rules and is developing constantly[29–31].Wang et al.[27]used fuzzy set theory to make the uncertainty quantitative in failure analysis in RPN.Failure modes’risk factors with their relative weights can be evaluated through the method.However,in situations where the systems are lack of experimental data,the fuzzy weighted geometric mean method(FWGM)proposed by Wang et al.[27]cannot be used.
Dempster-Shafer (D-S) evidence theory is another effective method to deal with uncertainty[32,33].Yang et al.[34] applied D-S evidence theory in handling uncertain evaluations of the risk factors in RPN.In their method,a modified D-S evidence theory is employed to gather different opinions with inaccuracy and uncertainty.However,in the situation that experts evaluate risk factors with different and accurate values,there will be highly conflict evidence in the basic belief assignments(BBAs) and Dempster’s combination rule can not fuse it.In order to avoid conflicting evidence in combination in FMEA,the boundaries of the focal elements are made fuzzy and a new BBA is constructed through the method to handle conflicting evidence [35].However,in Su et al.’s method[35],the generalization is not complete and the basic assumption of D-Sevidence theory that the basic elements in the frame of discernment are mutually exclusive is unrealistc.Thus,D numbers which can be seen as the generalization of D-S evidence theory is also investigated in the RPN evaluation in FMEA [36–38].It can represent both mutually related uncertain information and incomplete situations.
Information in reality not only has uncertainty limits on values,but also has partial reliability.Zadeh [39] proposed Z-number to describe information more fully in reality.According to the definition of Z-number,a Z-number can be expressed asZ=(A,B).Z-number contains two parts:the first partArepresents the uncertainty of the valuation;the second partBmeasures the reliability of partA.Z-numbers has attracted many researchers’attention and has been developing quickly[40–42].To represent the reliability in uncertain valuations,Jiang et al.[43]utilized Z-number[39]in FMEA.The method of Jiang et al.’s[43]is practical and useful since it takes the reliability part(experts’confident part) into consideration and does not need to define a great number of if-then rules.However,the fuzzy weighted mean process for integrating Z-valuations in their method may get wrong results when the reliability partBis equal to zero or a specialized trapezoidal fuzzy set with the same four numbers(which means the reliability part is a crisp number).
In this paper,an improved method based on the Z-numbers and the graded mean integration representation method is proposed.The subsequent parts of the paper are structured as follows.In Section 2,basic concepts are briefly reviewed.In Section 3,a new method based on Z-number and the graded mean integration presentation is proposed.In Section 4,two examples are given to point out the advantages of the proposed method.In Section 5,a case study is used to illustrate the application of the proposed method and compare results with other methods.Section 6 provides concluding remarks.
2 Preliminaries
2.1 Risk Priority Number(RPN)
RPN is the product of three risk factors,i.e.,the occurrence(O),severity(S)and detection(D)of a failure.It is always expressed as Eq.(1):

whereSis the severity of a failure effect,Ois the probability of occurrence of a failure mode andDis the probability of a failure being detected.Each risk factor is evaluated using the 10 ratings from 1 to 10.Take risk factor Occurrence(O)as an example(see Table 1):if the probability of occurrence of the failure is nearly impossible(i.e.,the possible failure rate ≤1/1,500,000),then the rating is evaluated as“1”;if the probability of occurrence is extremely high(failure almost inevitable,the possible failure rate ≥1/2),then the rating is evaluated as“10”[34].The failure modes whose RPNs are higher are considered riskier and will be ranking in higher positions for revision.
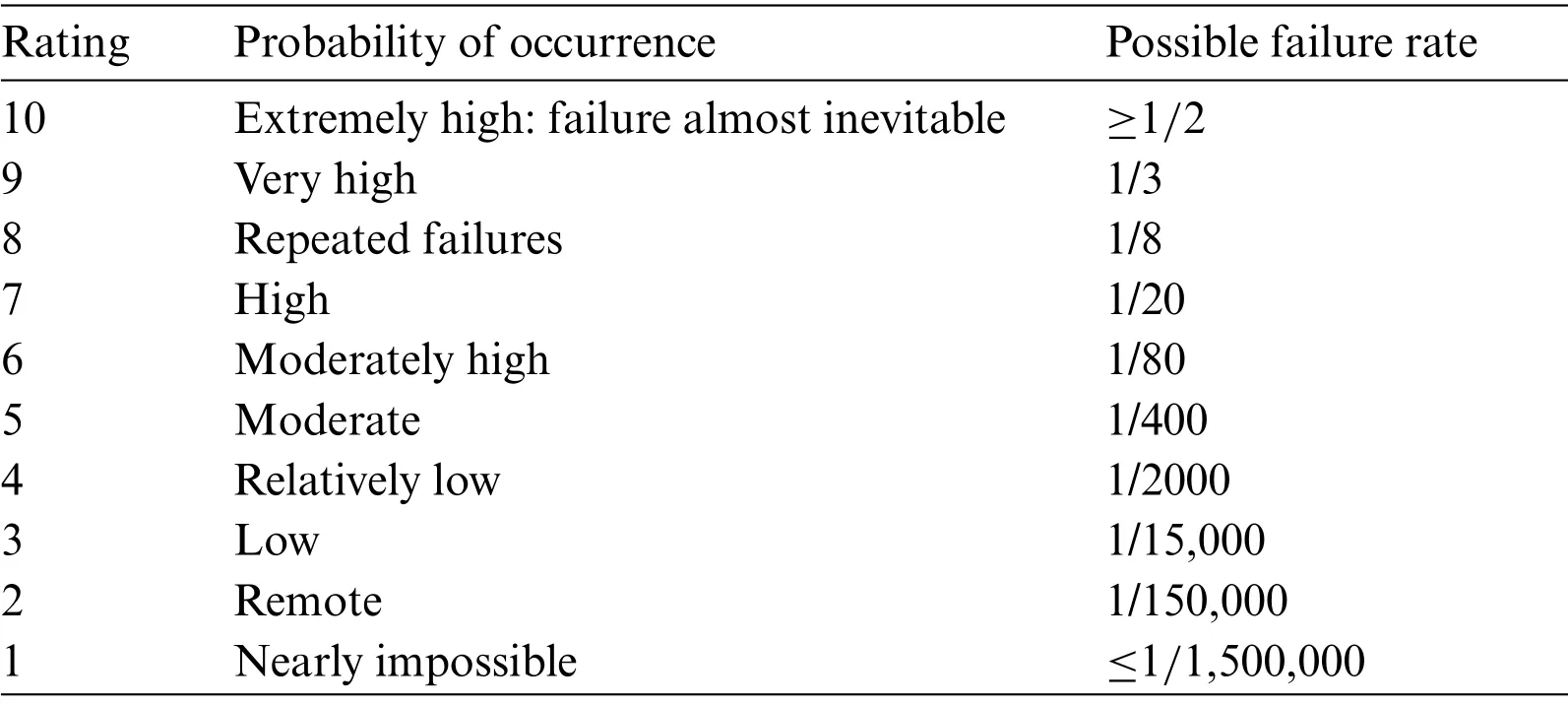
Table 1: Suggested criteria of rating for occurrence of a failure in FMEA[34]
2.2 Fuzzy Numbers
Information that is uncertain and indistinct can be represented by fuzzy numbers[44].
Definition 2.2.1A discrete and finite fuzzy setAwhich membership function isμA(χ)→[0,1]in the universe of discourseXis defined as Eq.(2)[45,46]:

Definition 2.2.2Fuzzy sets can be expressed with intervals,which are namedα-level sets.AssumeAis a fuzzy set on the universe of discourseX,theα-level sets ofAare defined as Eq.(3)[44]:
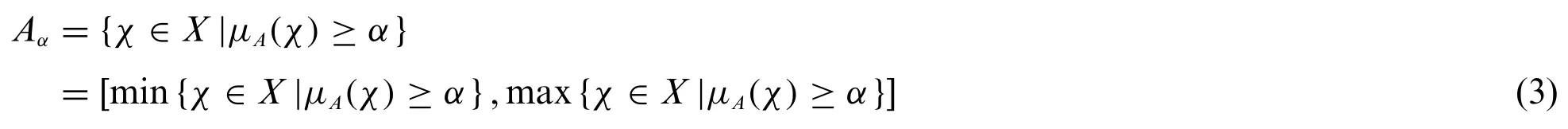
The defuzzified centroid ofAαis determined as Eq.(4):
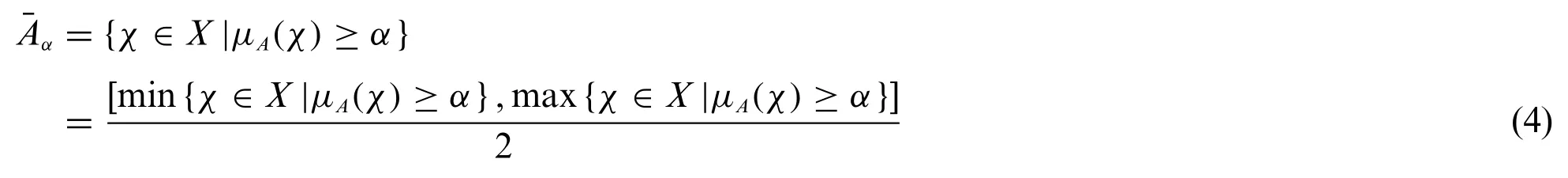
Definition 2.2.3A discrete triangular fuzzy numberAand a discrete trapezoidal fuzzy numberAwith membership functionμA(χ)→[0,1]in the universe of discourseXare respectively defined as Eqs.(5)and(6)[44]:

Definition 2.2.4In Fig.1,a,b,c,anddare real numbers.The fuzzy numberAin general is defined asA=(a,b,c,d;ωA)LR.WhenωA= 1,the notation is simplified asA=(a,b,c,d)LR.L-1andR-1,respectively,are the inverse functions of the functionsLandR./2 is the graded meanh-level value of numberAin general.Then,the graded mean integration ofAis represented as Eq.(7)[47]:

Figure 1:The graded mean h-level value of generalized number A=(a;b;c;d;ωA)LR[47]
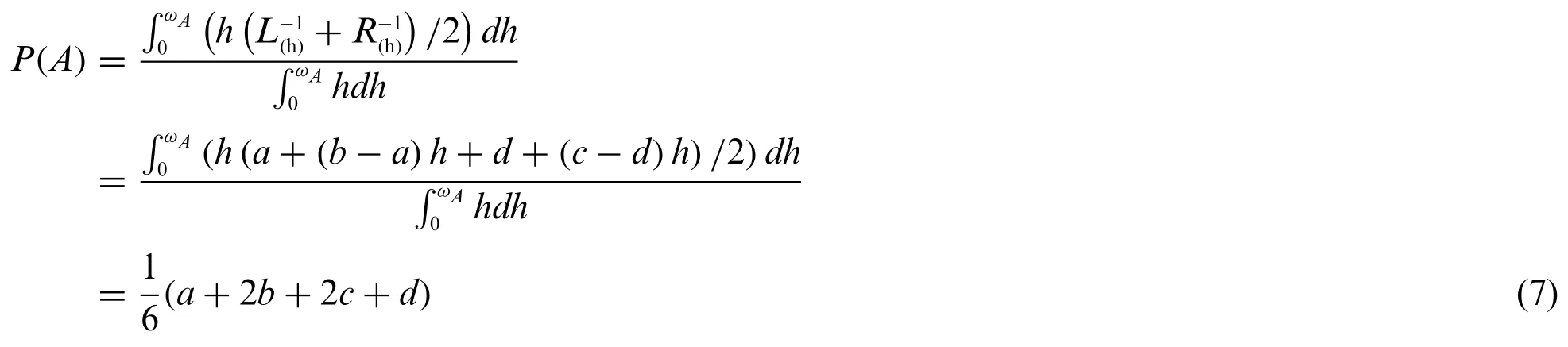
whereh∈[0,ωA]andωA∈[0,1].
2.3 Z-Number
Zadeh proposed Z-numbers’contents in 2011 [39].According to Zadeh,the Z-number is a pair of ordered fuzzy numbers expressed asZ=(A,B),the first componentAlimits values of uncertain variableXand the second componentBmeasures the reliability of componentA.
IfXis a random variable with probability density function,p(X)andZ=(A,B),where the componentAis a continuous fuzzy number to limit the possibilistic of variableXand the componentBis a fuzzy constraint on the probability(reliability)of the componentA.In effect,the Z-valuation(X,A,B)is a limitation onXexpressed as Prob(XisA)isB.Thus,probability of the eventp(X)is expressed as Eq.(8):

whereμA(u)is the degree to whichusatisfies the constraint,px(u)is the probability density ofX.
Some examples of Z-valuations are given below:
(dogs’life,nearly 15 years,likely);
(size of German,about 36 million hectares,very sure);
(level of Sam’s effort,low,not sure).
3 Improved FMEA Method Based on Z-Numbers and GMIR
In this section,a new method is proposed to rank failure modes.There are much uncertain information to deal with in FMEA.With the development of Z-number,as it can express both possibility and reliability,large numbers of studies apply the Z-number to the risk priority numbers in the FMEA.However,the use of fuzzy weighted mean to integrate the Z-valuations of failure mode are not greatly suitable.
This article uses the graded mean integration representation (GMIR) method to integrate Zvaluations and propose a new method for calculating the risk priority numbers.
As is shown in Fig.2,assume the potential failure modes in the system are previously identified based on historical data,the procedures of the new method are as follows.

Figure 2:Procedures of the new method
Step 1:Construct Z-numbers based on evaluations of risk factors(O,S,D)for each failure mode by different experts.
Assume that there areMpotential failure modes in FMEA and each potential failure mode includes three risk factors.And,there areKexperts making evaluations.In a Z-number,the componentAandBare modeled as trapezoidal fuzzy number set and triangle fuzzy number set,respectively.
The risk factoruiin failure modemevaluated by thekth expert can be represented with a triplet as Eq.(9):

wherem= 1,2...,M,i= 1,2,3,ui|i=1,2,3= {O,S,D},k= 1,2...,K,represents the possibility of risk andrepresents the reliability of risk.FMmuirepresents the risk factoruiof failure modem,where(r= 1,2,3,4)is defined within the interval[0,10] and(g= 1,2,3)is within the interval [0,1].Then the Z-evaluation represented ascan be written aswith the fuzzy number.
Step 2:Determine the weights of experts and risk factors.
Weights of experts and weights of risk factorsO,S,Din FMEA are usually investigated by decision support group by using weight determination methods such as Analytic Hierarchy Process[48].
Step 3:Obtain integrated representation of Z-numbers based on GMIR method.
In this step,we obtain integrated representation of Z-numbers(ZGO,ZGS,ZGD)on the basis of the graded mean integration method as defined in Eq.(7).
Definition 3.1The integrated representation of Z-numbersZGO,ZGSandZGDare defined as Eq.(10):
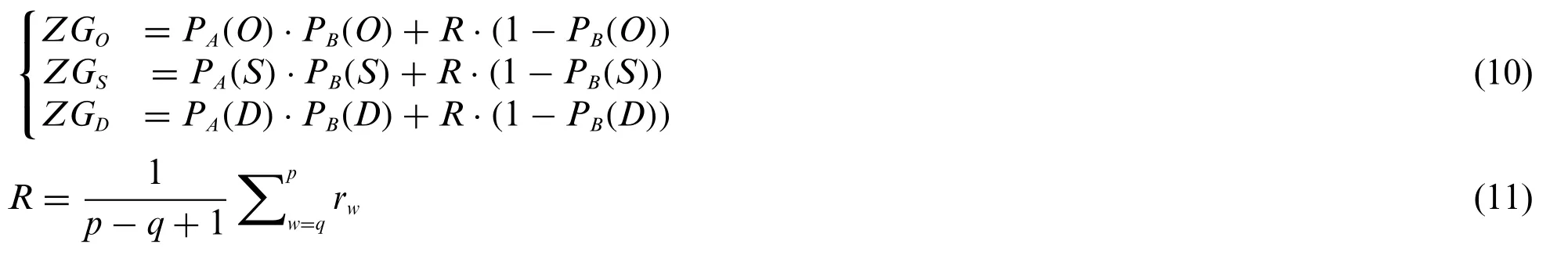
whereZGO,ZGSandZGDare the integrated representation of Z-numbers based on evaluations of risk factorsO,S,D,respectively;PA(O),PA(S)andPA(D)are the graded mean integration representation of partAin risk factorsO,S,Daccording to Eq.(7);Rin Eq.(11)is the mean value of ratings for risk factorsO,S,D,qis the minimum sequence number of ratings andpis the maximum sequence number of ratings,rwrepresented variables changed between minimum value and maximum value of the ratings.Take“Occurrence”for example,q=1,p=10,rw=1,2,...9,10,andR= 5.5.Ris adopted here to handle the unreliable(unconfident)part.PB(O),PB(S)andPB(D)∈[0,1] are the graded mean integration representation of the reliability partBin evaluations of risk factorsO,S,Daccording to Eq.(7).
Step 4:Calculate the ZGRPNs of failure modes.
In this step,the integrated representations of three risk factors(ZGO,ZGS,ZGD),are multiplied to gain the ZGRPN,which means the RPN are derived from Z-numbers and the graded mean integration representation.The definition of ZGRPN are as follows:
Definition 3.2Assume the system hasMfailure modes,Kexperts and three risk factors,the ZGRPN of themth failure mode from thekth expert is defined as Eq.(12):

wherei=1,2,3,ui|i=1,2,3={O,S,D};ωuimk(i=1,2,3)represents the weight of risk factoruiof failure modemfrom thekth expert andrepresents the integrated representation of the Z-number based on evaluations of risk factoruiin failure modemfrom the kth expert.
Step 5:Calculate the ZGRPN’s of failure modes and give the failure modes’rankings in descending order of the ZGRPN’s.
In this step,evaluations fromkdifferent experts about one specific failure modem()are combined to gain the comprehensive evaluation(ZGRPN)based on the weighted average method.
Definition 3.3Assume that there areKexperts,the ZGRPN’of themth failure mode fromkexperts is defined as Eq.(13):

whereωkis the weight of thekth expert andk=1,2...,Kand
Then give the failure modes’rankings in descending order according to the ZGRPN’s.The failure modes with higher ZGRPN’are riskier(have higher priority)and should be paid more attention to.
4 Numerical Examples
To show the validity of modified method,two examples are given in this section.
To make the calculation simple,we assume that risk factorsO,S,Dhave the same weight in this paper.
Example 1.Suppose that Z-numbers based on evaluations of risk factorsO,S,Dhave the same componentA(possibility) and the componentB(reliability part) is equal to zero or a specialized trapezoidal fuzzy number with four same coordinate values which means that the fuzzy number degenerates into crisp number(as shown in Table 2).~Vis the integrated representation of Z-numbers in Jiang et al.’s method[43];ZRPN is the RPN derived by Jiang et al.’s method[43];(ZGO,ZGS,ZGD)is the proposed integrated representation of Z-numbers of three risk factorsO,S,Dbased on GMIR method;ZGRPN is the RPN derived by the proposed method.
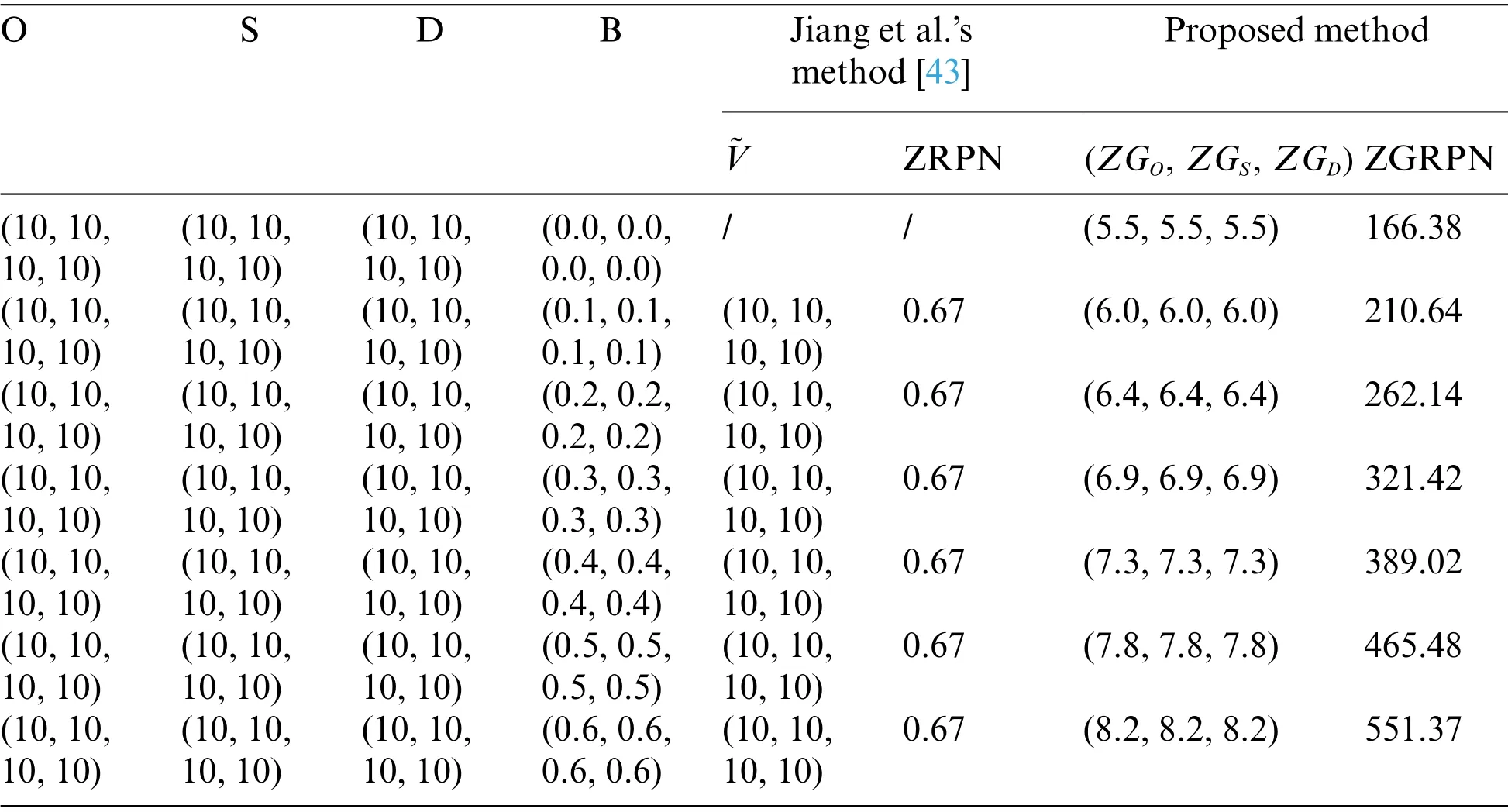
Table 2:The integrated representation of Z-numbers and the RPN in the situaton that B is a specialized trapezoidal fuzzy number
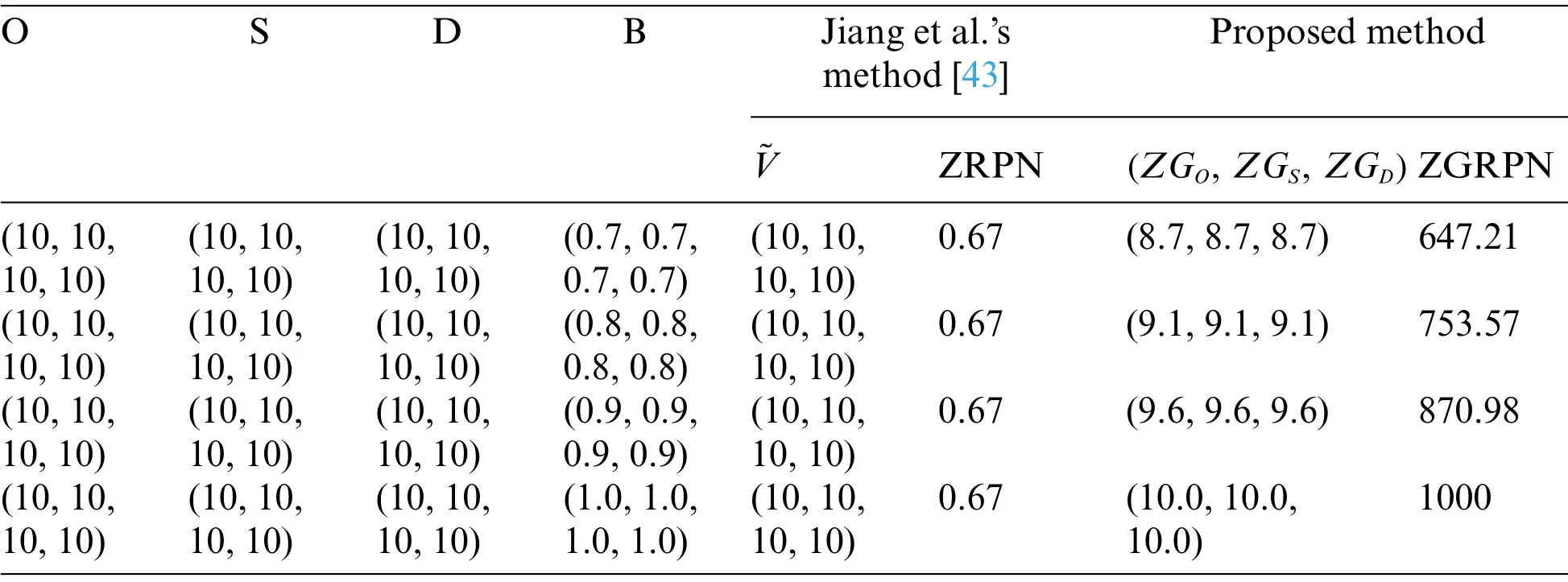
Table 2 (continued)
As can be seen from Table 2,in the situation that the componentB(reliability part)is a specialized trapezoidal fuzzy number with four same coordinate values,the value of ZRPN does not change when partBchanges.This means that,in such case,the partBdoes not work.Especially,when the partBis equal to zero,Jiang et al.’s method[43]cannot handle such situation since the denominator in the fuzzy weighted mean formula becomes zero.Different from ZRPN,the value of ZGRPN obtained by the proposed method increased with increasing value of partB(reliability).This is reasonable:as can be seen from Table 2,partAof risk factorsO,S,Dbelongs to the highest rating(the most risk),the priority of such failure mode should be promoted with a higher confidence level(reliability).
Example 2.Assume that the Z-number constructed based on the evaluation of risk factor is Z=(A,B)=((7,8,8,9),(6,6,6.3,6.3)).Now assume that partAdoes not change,partBchanges from(6,6,6.3,6.3)to(5.7,6,6.3,6.3).In such case,since partAshows high risk(higher than average rating“5”)for a certain risk factor,if partB(reliability of partA)decreases,the risk priority of such case will decrease accordingly.The integrated representations of Z-numbers under these two cases are given in Table 3.is the integrated fuzzy number of Z-number derived by Jiang et al.’s method[43]and ZG is the integrated crisp number of Z-number based on GMIR derived by the proposed method.

Table 3: The integrated representations of Z-numbers under two cases
As can be seen in Table 4,the integrated representation of Z-number by Jiang et al.’s method[43]is in the form of a fuzzy number which is difficult to compare.Thus,we first defuzzify the fuzzy set by the centroid defuzzification method.Setαlevels as 0,0.1,0.2,...,1.0(as shown in Fig.3).is the centroids of thecomputed by Eq.(4).The defuzzified centroid values ofare shown in Table 4.
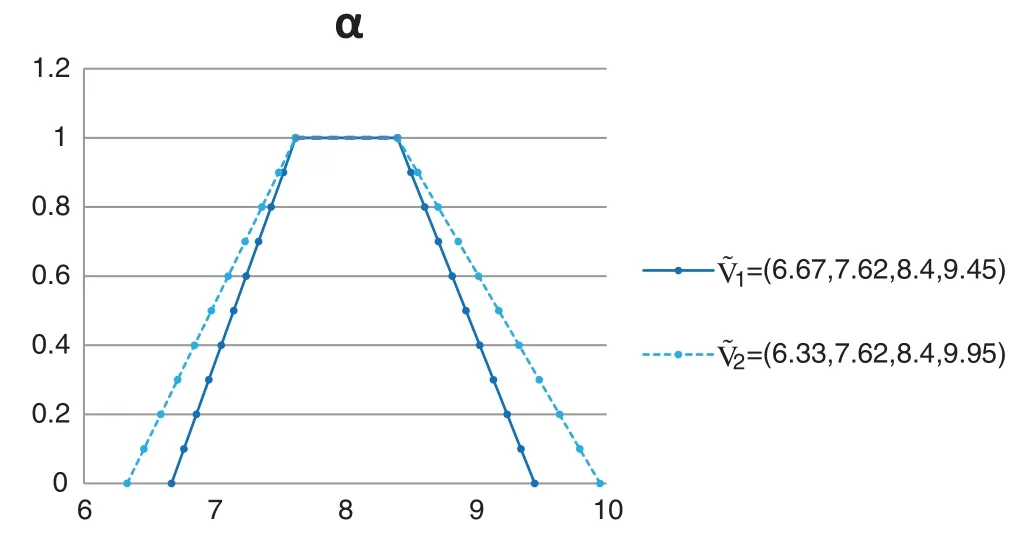
Figure 3:α-level cuts of the integrated valuationsin two cases
Table 4: The centroids of of the two cases
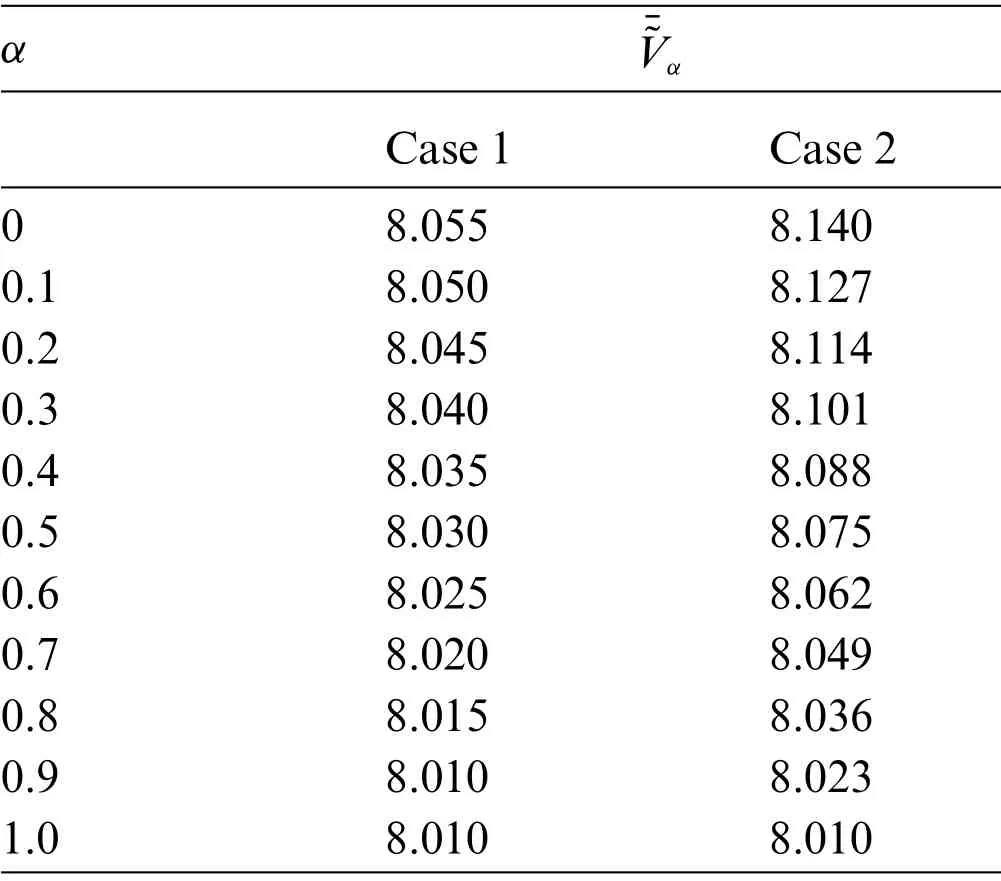
Table 4: The centroids of of the two cases
α¯~Vα Case 1 Case 2 0 8.055 8.140 0.1 8.050 8.127 0.2 8.045 8.114 0.3 8.040 8.101 0.4 8.035 8.088 0.5 8.030 8.075 0.6 8.025 8.062 0.7 8.020 8.049 0.8 8.015 8.036 0.9 8.010 8.023 1.0 8.010 8.010
It can be seen from Tables 3 and 4,in Jiang et al.’s method[43]that when the partAshows high risk evaluation,with the reliability of partA(partB) decreases,the integrated valuation ~V(which combine partsAandB)of risk level even increases(in other words,the value of ZRPN increases).Such phenomenon is contrary to common sense.By using the proposed method,when partB(reliability of partA) decreases,the integrated representation of risk evaluation (ZG,or ZGRPN since no more experts are considered here)will decrease accordingly.This is in accordance with the common sense.
5 Case Study
In this section,a case study of prioritizing risk levels of failure modes in an aircraft turbine’s rotor blades system from reference[43]is given to show the use and effectiveness of the proposed method.
Seven failure modes are identified and analyzed in the aircraft turbine’s rotor blades system.Assume that there are three experts and their weights are 0.4,0.3,0.3,respectively.And suppose the Z-numbers based on evaluations of risk factorsO,S,Dhave the same reliability partsB,B=0.8,and the possibility partsAare shown in Table 5.The integrated representation of Z-numbersZGO,ZGSandZGDare also shown in Table 5.The ZGRPN’s and the rankings of seven failure modes obtained by the proposed method are given in the last two columns of Table 6.
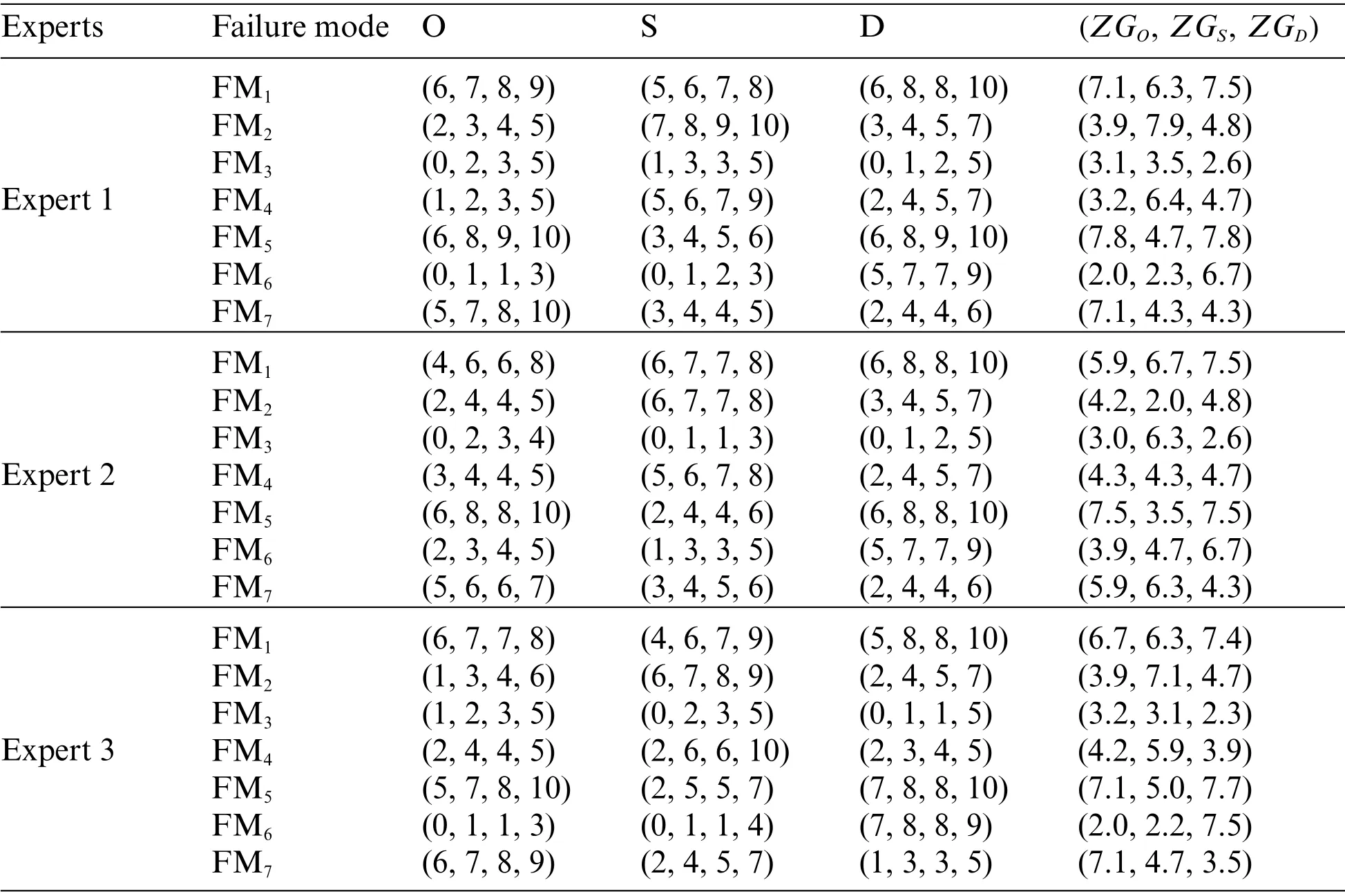
Table 5:The possibility parts A and the integrated representation of Z-numbers based on evaluations of three risk factors
In Table 6,the new proposed method(ZGFMEA method)is compared with the traditional RPN method[49],Wang et al.’s FWGM method[27]and Jiang et al.’s ZFMEA method[43].
It can be seen from Table 6 that the ranking of the failure modes by the proposed method is the same as the traditional RPN.That isFM1>FM5>FM7>FM2>FM4>FM6>FM3.The rankings of failure modes 2 and 7 in the proposed method are opposite to the FWGM method and the FMEA method,with slight difference between RPNs of these two failure modes.The reason may be that in the FWGM method and ZFMEA method,the fuzzy weighted mean is adopted to integrate the evaluations which may lead to unreasonable results under some situations.What’s more,the values of RPNs calculated by the proposed method(i.e.,ZGRPN’)show larger difference among them,which means the proposed method is more sensitive to differences and is more useful for decision making.

Table 6: Comparisons of the results
6 Conclusion
This paper proposed a new method based on Z-numbers and the graded mean integration representation (GMIR) to handle the risk priority ranking problem in FMEA.Z-numbers are used to model the uncertainty of the evaluation results of the risk factorsO,S,andD.The graded mean integration representation method is used to help integrate the Z-evaluations.Two examples and the case study are used to illustrate the superiority of the proposed method: the proposed method can handle some situations while other methods cannot,e.g.,when partAshows high risk (higher than average rating“5”)for a certain risk factor,if partB(reliability of partA)decreases,the risk priority of such failure mode will decrease accordingly with the proposed method which is intuitive;the ranking of failure mode by the proposed method is basically consistent with other methods in the case study,and the result of ZGRPN’is more sensitive to differences and is more useful for decision making.In the proposed method,partAand partBof a Z-number are constructed directly on experts’opinions.In subsequent research,we will further investigate the construction of Z-numbers based on numerical data.Also,how to make full use of partBof a Z-number is a promising issue.
Funding Statement:The work is partially supported by Shanghai Rising-Star Program (Grant No.21QA1403400),Shanghai Natural Science Foundation (Grant No.19ZR1420700),Shanghai Key Laboratory of Power Station Automation Technology(Grant No.13DZ2273800).
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- An Extended Fuzzy-DEMATEL System for Factor Analyses on Social Capital Selection in the Renovation of Old Residential Communities
- Analysis and Power Quality Improvement in Hybrid Distributed Generation System with Utilization of Unified Power Quality Conditioner
- An Effective Machine-Learning Based Feature Extraction/Recognition Model for Fetal Heart Defect Detection from 2D Ultrasonic Imageries
- Monitoring Study of Long-Term Land Subsidence during Subway Operation in High-Density Urban Areas Based on DInSAR-GPS-GIS Technology and Numerical Simulation
- Static Analysis of Anisotropic Doubly-Curved Shell Subjected to Concentrated Loads Employing Higher Order Layer-Wise Theories
- Slope Collapse Detection Method Based on Deep Learning Technology
