Self-Triggered Consensus Filtering over Asynchronous Communication Sensor Networks

Huiwen Xue,Jiwei Wen,★,Akshya Kumar Swain and Xiaoli Luan

1Key Laboratory of Advanced Process Control for Light Industry(Ministry of Education),Jiangnan University,Wuxi,214000,China

2Department of Electrical,Computer and Software Engineering,University of Auckland,Auckland,0632,New Zealand

ABSTRACT In this paper,a self-triggered consensus filtering is developed for a class of discrete-time distributed filtering systems.Different from existing event-triggered filtering,the self-triggered one does not require to continuously judge the trigger condition at each sampling instant and can save computational burden while achieving good state estimation.The triggering policy is presented for pre-computing the next execution time for measurements according to the filter’s own data and the latest released data of its neighbors at the current time.However,a challenging problem is that data will be asynchronously transmitted within the filtering network because each node self-triggers independently.Therefore,a co-design of the self-triggered policy and asynchronous distributed filter is developed to ensure consensus of the state estimates.Finally,a numerical example is given to illustrate the effectiveness of the consensus filtering approach.

KEYWORDS Self-triggered policy;sensor networks;distributed consensus filtering

1 Introduction

A wireless sensor network (WSN) is composed of a large number of sensor nodes distributed in a specific area.With the development of sensing,cloud computing,and wireless communication technologies,WSN has been successfully applied in a variety of practical environments,such as battlefield monitoring,target tracking,health monitoring,search and rescue operations after disasters,industrial automation,and so on [1,2].However,noise ubiquitously exists in signal transmission and WSN environment,which often results in degradation of the filtering performance.Therefore,distributed filtering obtains an ever-increasing attention when estimating unavailable states through measured outputs and historical data[3–5].Compared with traditional centralized filtering[6],each sensor node finalizes filtering according to its own and neighbors’data under a fixed interconnection topology within a distributed filtering network.Therefore,distributed filtering is robust to sensor failures and transmission constraints.

Usually,the sensor is powered by a lithium battery and has a limited capacity for memory.Therefore,it is of great significance to reduce communication and computation energy loss.Traditional timetriggered sampling requires signal transmission to be continuous or periodically updated.Although it is conducive to analysis and design,the rate of signal update is constant and quick,and may lead to waste use of limited communication resources.In addition,the narrow network bandwidth may lead to channel congestion,induced delay and data packet drop out[7,8],etc.The key to solving these problems is to reduce the transmission load on the premise of good filtering performance.

Therefore,event-triggered mechanisms(ETM)[9–11],which can greatly reduce the unnecessary data transmission and resource occupation,are developed with burgeoning research interests.In the past few years,the main progress of ETM for distributed filtering can be generally divided into four categories,i.e.,triggering based on constant threshold [12–14],instantaneous measurement-/estimate-dependent threshold [15–17],released measurement-/estimate-dependent threshold [18–21]and dynamic event-triggering [22,23].The first three categories can be summarized as static eventtriggered mechanisms(SETM),which has a fixed scalar triggering threshold.In contrast,the fourth class is named as dynamic event-triggered mechanisms (DETM),which can adjust the triggering threshold.Aiming at distributed set-membership estimation for time-varying systems,a new DETM designed in[23]leads to larger average inter-event times and thus less totally released data packets.

It is worth noting that ETM are more effective in reducing transmission frequency compared to traditional time-triggered sampling at the cost of increased computational burden [24].Specifically,in order to check whether the triggering conditions are met,the above ETM strategies embedded in the sensor nodes have to continuously make judgments at each sampling instant.For a large-scale WSN,there is numerous computational burden consumption.In order to overcome this shortcoming,a self-triggered policy was first proposed in [25] to optimize the allocation of computing burden and performance for real-time systems containing multiple control tasks.Since such a scheme precalculates the next update moment through the current samplings,the self-triggering is an active behavior.Up to now,the self-triggering policy is mostly employed in control systems [9,26–32] and it still remains open for solving filtering problems.The main motivation of this study is to shorten the gap between self-triggering theory and its applications to distributed filtering.

The main contributions of this paper are summarized as follows:

1.For a filtering network,a self-triggered policy is designed to save transmission energy and computational burden,especially in a large-scale WSN.Unlike the ETM,the self-triggered policy can predict the subsequent execution time in advance without checking the triggering conditions at each sampling time.That is,the next triggering interval is calculated based on the latest transmission data,the latest state estimates of itself and neighboring nodes.

2.In filtering networks,since each filtering node is triggered independently and has its own triggering interval,this will lead to an asynchronous transmission phenomenon.Through the co-design of self-triggered policy and distributed consensus filtering,even when the WSN encounters asynchronous communication,the filtering system can maintain good state estimation.

2 Preliminaries and Problem Formulation

Consider a sensor network withnnodes to monitor the plant and estimate its states.The directed weighted graphG=(V,E,A)is used to model the network topology of interacting sensors,whereV={1,2,...,n}denotes an index set of sensor nodes,E⊆V×Vrepresents the edge of paired sensor nodes andA=stands for the weighted adjacency matrix.The adjacency elementaij ＞0 ⇔(i,j)∈Erepresents a positive weighting of the edge between two adjacent sensors,which implies that sensorireceives data from sensorjor sensorjtransmits data to sensori,otherwise,aij=0 if no data link exists between sensorjto sensori.In addition,we assumeaii= 1 for alli∈Vand(i,i)can be considered as an additional edge.The set of neighbors of nodeiincluding the node itself is denoted byNi= {j∈V:(i,j)∈E}.The Laplace matrix of the graphGis defined asL=D-A,whereD=diagn{di}with the diagonal elementdi=

Consider the plant described by a discrete-time linear system of the following form:

wherex(k)∈Rnxis the system state;z(k)∈Rnzis the output to be estimated;ω(k)∈Rnωis the external disturbance belonging tol2[0,∞);A,BandMare known constant matrices with appropriate dimensions.The initial statex(0)is an unknown vector.

For every sensori(i∈V),the model of sensor nodeiis in the form of

whereyi(k)∈Rnyis the measured output collected by nodei,vi(k)∈Rnvis measurement noise belonging tol2[0,∞),CiandDiare known constant matrices with appropriate dimensions.

In sensor networks,the data available for filter on the sensor node comes not only from the sensori,but also from its neighbors.Considering the consensus problem,the whole distributed filtering network can be constructed as follows:

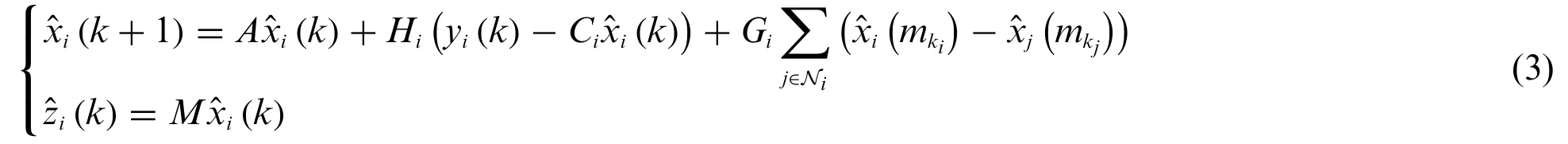
Assumption 1:We assume that sensors monitor the target plant at every sampling moment.Then we focus on reducing the communication frequency between sensors so as to achieve better resource efficiency.

The distributed self-triggered filtering system is illustrated in Fig.1.For example,the sensor nodeitransmits the measurementsyi(k)to the corresponding filteri.In the whole sensor network,each filter obtains the latest state estimationfrom its neighbors and transmits its own filtering resultsto other neighbors when meeting a well-defined condition.At each sampling instant,filtericalculates and updates its estimated stateand its time-stampkare integrated into a data packet.Similarly,the data packetis considered as the latest released data when the filteriis triggered.Buffericontaining multiple units is driven by self-triggered policy,and has the capability of checking the time stamps of the newly arrived data packetand discarding old data packets.In brief,the buffer can reserve the latest data packets until new data packets arrive.

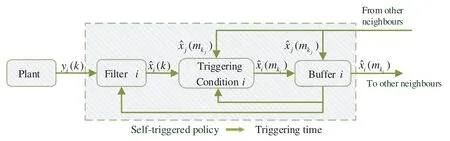
Figure 1:Block diagram of distributed self-triggered system

The self-triggered policy predicts the subsequent execution time and calculates the triggering interval by the latest data of each filter without a continuous judgment process.Therefore,the strategy proposed in this paper is beneficial to the energy saving of sensor networks with limited resources,as well as scant network channel bandwidth.

The self-triggered time-sequence diagram is illustrated in Fig.2.The dash lines indicate that data is exchanged between nodes and the arrow points to the object of data transmission.The broadcasting and receiving of the latest released state estimation are determined by the filter node’s own self-triggered policy.It is clear that each filter node has its own triggering time sequence,which causes different triggering intervals between each other.Moreover,for filteri,the time that data packets from neighbors arrive at bufferimay be asynchronous,since it is determined by different triggering conditions.Such an asynchronous transmission brings challenges to the design of consensus distributed filtering.

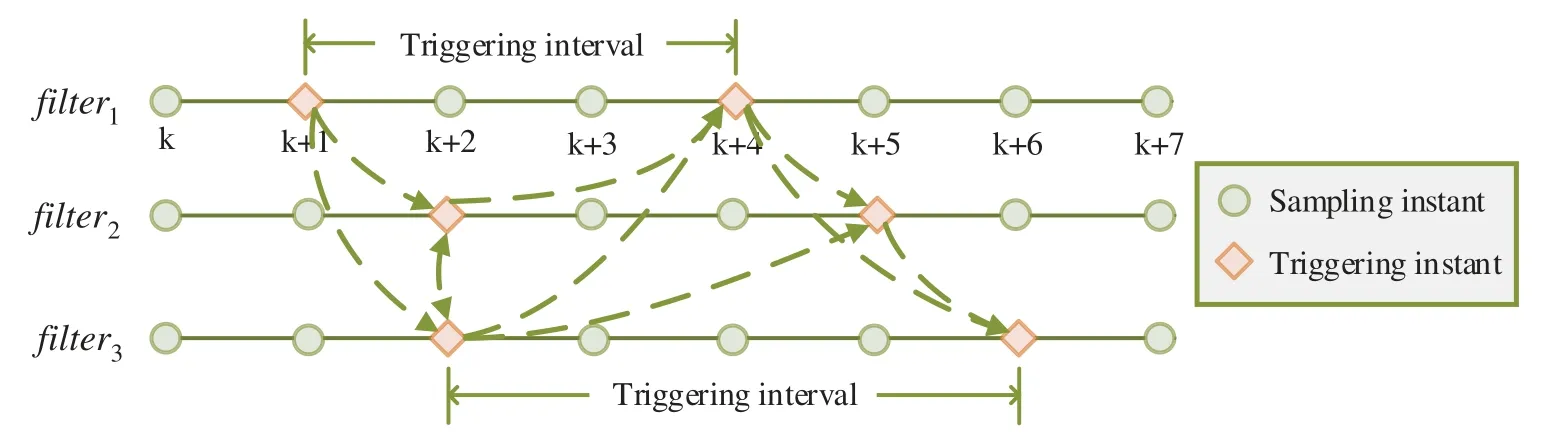
Figure 2:Self-triggered sequence diagram

For filteri,let’s define a state estimation error,an output estimation errorand a state estimation update error.Thencan be expressed as.Combing(1)–(3),the estimation error dynamics can be rewritten as

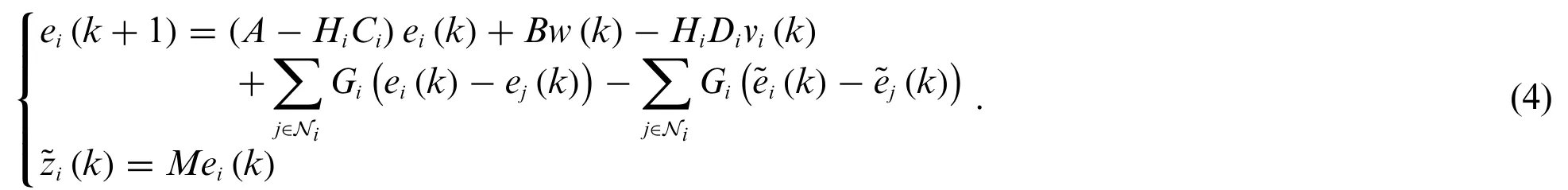
The topology of the sensor is determined by a given graphG=(V,E,A).For the sake of brevity,we denote

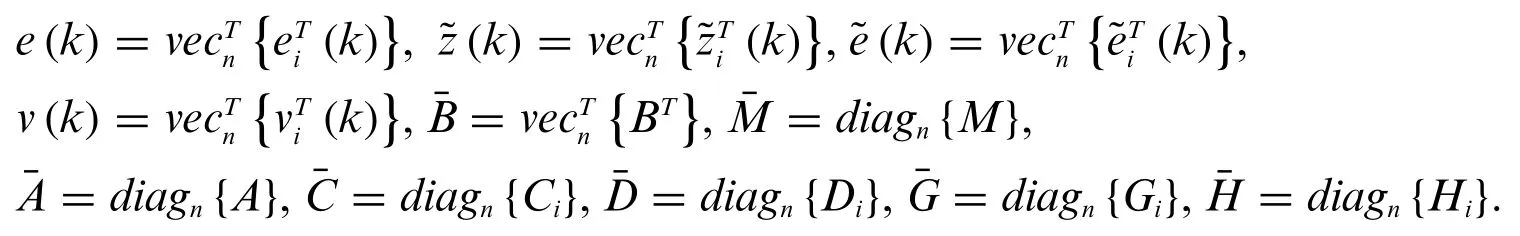
Then,the error dynamics governed by(4)can be rewritten in the following compact form:

Definition 1([27]):Filters (3) are said to be a distributed self-triggeredH∞consensus filtering system(1)if they meet the following conditions:

1)In the absence of system disturbance and measurement noise,the filtering error system(5)is exponentially stable,i.e.,there exist positive constantsηandα∈(0,1)such that limk→∞||e(k)||2≤ηαk,for allk≥0.

2) Under the condition of the system disturbance and measurement noises,the output filtering errors(k),∀i∈Vsatisfy the followingH∞performance:

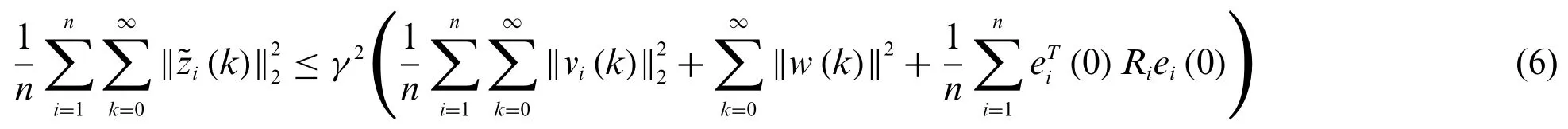
whereγ ＞0 is the attenuation level andRi=0 are some given positive definite matrices.

3 Main Results

In this section,we first design a distributed self-triggered policy.Based on such a policy,sufficient conditions are given for theH∞consensus analysis of the filtering error system (4).Furthermore,a co-design method for self-triggered threshold parameters and distributed filter gains is presented.

3.1 Self-Triggered Policy

The self-triggered policy predicts that the subsequent execution time depends on the current sampling data and the estimated state updated by its neighbors.Based on this idea,we develop selftriggered distributed filtering.The next triggering instant is considered as follows:

The key to realizing the self-triggered policy is to obtain the triggering interval functionMki(·).We develop the following error-based self-triggered policy:

whereδi=εi∈(0,1] is the threshold parameter; Φi∈ Rp×pis the weighting matrix tio be determined.

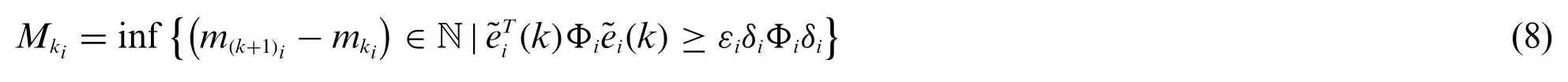
Theorem 1:In order to formulate a suitable self-triggered policy for the distributed filtering system(5),the triggering interval function can be expressed as

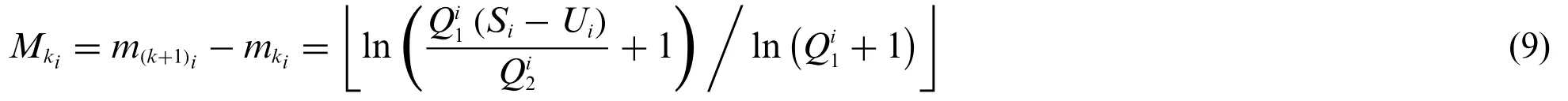
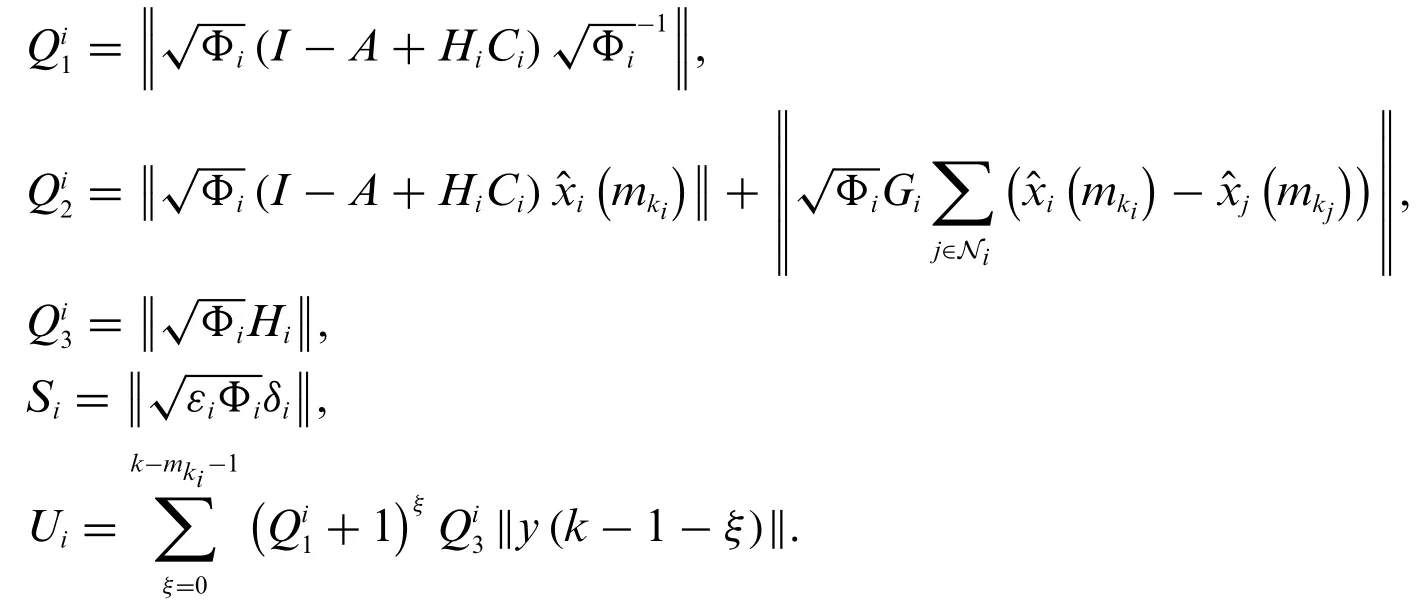
Proof:Combining relations(3)and(4),we can obtain

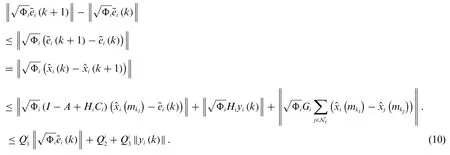
AssumeYi(k)=Then inequality(10)can be rewritten as

From(11),we can obtain

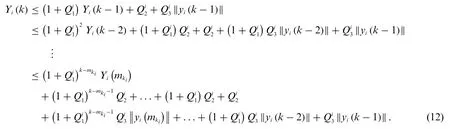
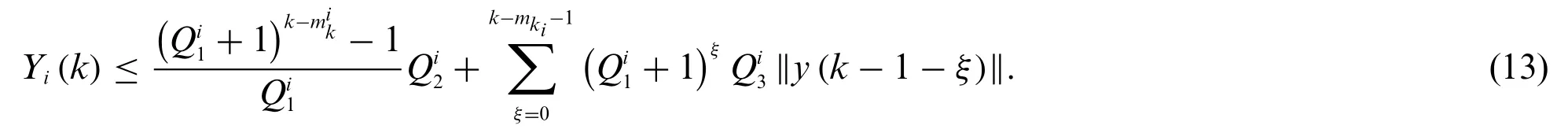
According to self-triggered condition(8),if the filter nodeiis triggered,the following inequality is obtained

Combining inequality(13)and(14),we have

Through the simple mathematical manipulation of(15),triggering interval(9)is derived.

To guarantee the system performance,the current state estimation of the filter nodeishould be broadcasted to other neighbors immediately once the triggering conditions are satisfied.This means that the triggering intervalMkishould be rounded up.The proof is completed.

3.2 H∞Consensus Performance Analysis

Lemma 1:Given a positive definite matrix＞0(1 ≤i≤n),the filtering error system(4)is exponentially stable and satisfyH∞consensus performance under the self-triggered policy(9)and the initial conditionif there exist a positive scalarγ ＞0 and real symmetric matricesPi ＞0,satisfying

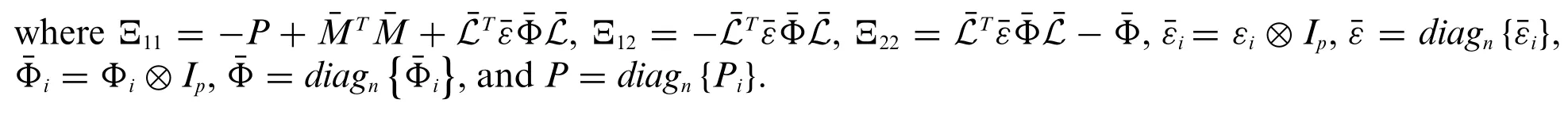
Proof:Consider a Lyapunov function

The one-step time difference is

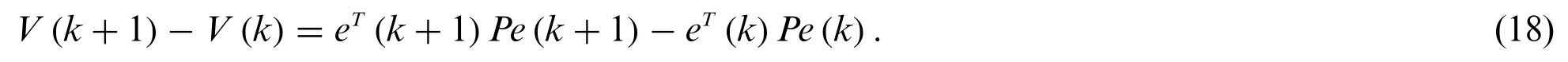
According to the self-triggered policy(9),the following inequality in augmented form is valid for[mki,m(k+1)i)

where Ψ is a real symmetric matrix,and others are zero matrices.

Therefore,Eq.(18)can be rewritten into the following inequality

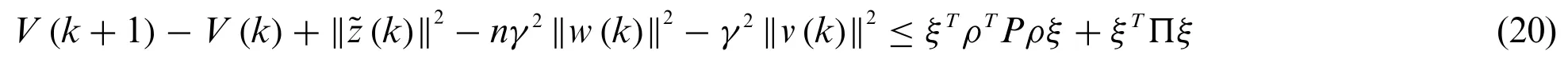
whereξT=[eT(k),(k),vT(k),wT(k)],ρT=,Π11=and others are zero matrices.

We assume that

By applying Schur complement lemma to(20),we obtain

whereϒ=Pρ=

First,we prove that the system (4) is exponentially stable when there is no disturbance and measurement noises.Denotingλ1=λmax(Γ),obviouslyλ1is smaller than zero,which indicates that(20)satisfies

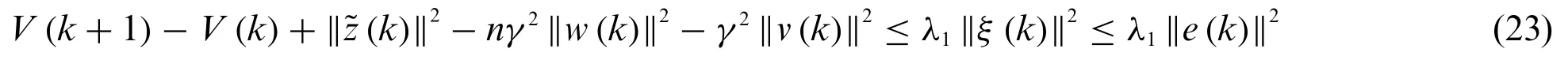
Defineλ2=λmax(P)＞0.Then given positive scalarμ,from inequality(23),we obtain

With some simple mathematical managements,we get

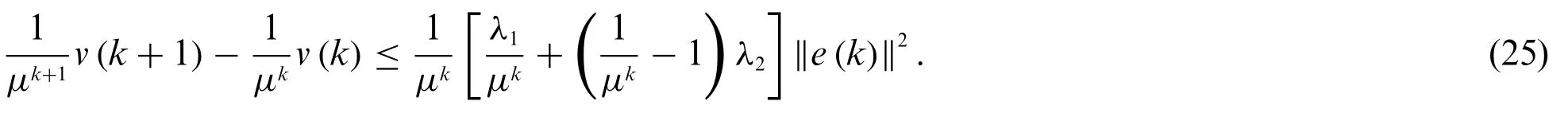
whereλ3=λmin(P) ＞0.Whenkapproaches to infinity,we can obtain limk→∞||e(k)||2= 0 which implies estimation error system(4)is exponentially stable.

Second,it follows from(20)and(21)that

Summing up both sides of(27)from 0 totwith respect tok

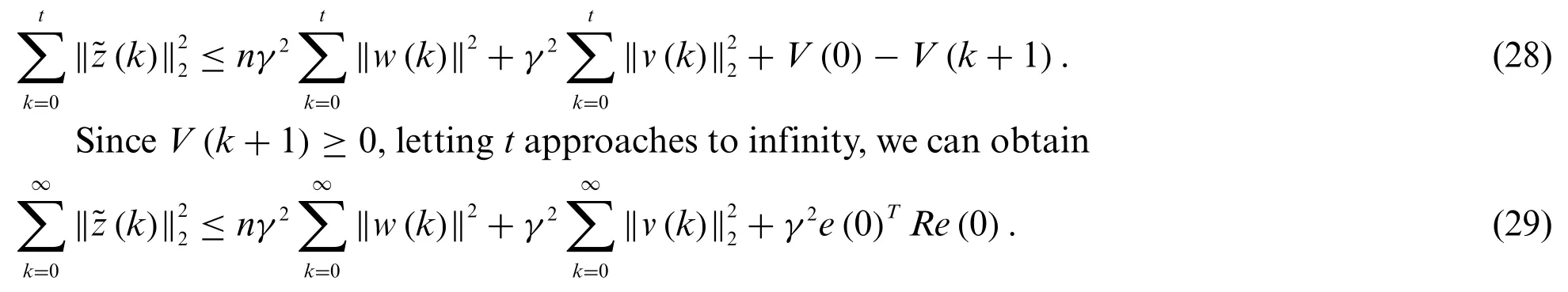
Therefore,the filtering error system also satisfies theH∞filtering performance condition in Definition 1.The proof is completed.

3.3 Co-Design of Self-Triggered Policy and Asynchronous Distributed Filter

The above Theorem and Lemma will be employed to design distributed self-triggered consensus filtering network(3),which leads to the following theorem.

Theorem 2:Given a positive definite matrixRi=0(1 ≤i≤n),the distributed self-triggered filtering problem is solvable,if there exist a positive scalarγ ＞0,real symmetric matricesPi=0,,and real matricesXi,Yisatisfying

initial conditions

and the following set of linear matrix inequalities

whereX=

Moreover,if the set of linear matrix inequalities(31)with(30)is feasible,the filter gains can be computed as

Proof:DenotingXi=PiHi,Yi=PiGi.Then we have

Substituting relations(33)into inequality(16),it can be seen that the inequality(16)in Lemma 1 results in inequality(31)with(30).The proof is completed.

Remark 1:The goal of the above co-design is to conquer the asynchronous communication caused by self-triggered policy and achieve good filtering performance.Through Theorem 2,the self-triggered threshold parameters Φiand the filter gain matricesHi,Gicould be successfully solved together.

4 Numerical Example

In this section,a numerical example is given to demonstrate effectiveness of the above co-design.

The network topology is represented by directed weighted graphG=(V,E,A)with five nodesV= {1,2,3,4,5},set of edgesE⊆{(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(3,2),(3,3),(3,4),(4,1),(4,4),(5,3),(5,5)}.The transmission paths between five nodes in Fig.3 and adjacency matrix as follows:

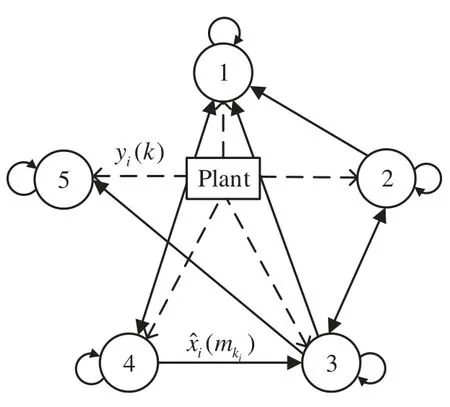
Figure 3:Schematic of distributed filtering over the WSN

The simulation is taken as 300-time units and each unit length is taken as 0.1.The system and sensor parameters are given as

The system noise and measurement noise are taken asω(k)=e-2kandvi(k)=[e-2ksin(k)2e-kcos(2k)],respectively.The initial statex0=The initial estimation of each nodeiare given as

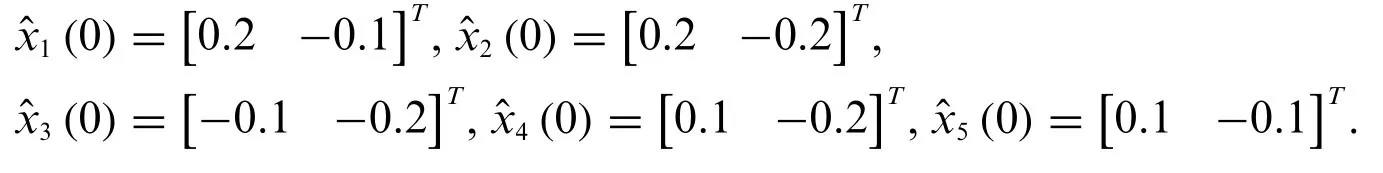
The self-triggered parameters of each nodeiare taken asε1= 0.7,ε2= 0.2,ε3= 0.6,ε4= 0.4,ε5=0.3.The positive definite matrices are givenR1=R2=R3=R4=R5=diag2{0.7}.

To further verify the strength of the self-triggered consensus filtering,a rectangular pulseωd(k)as an external disturbance is introduced into the system whenk∈[8,10].The simulation results are shown in Figs.4–6.

The outputz(k)and its estimation are depicted in Fig.4.The filtering root means square error is given in Fig.5.They show that the designed self-triggered consensus filter performs well in tracking the state of the target plant and the system has good robustness under the self-triggered policy.

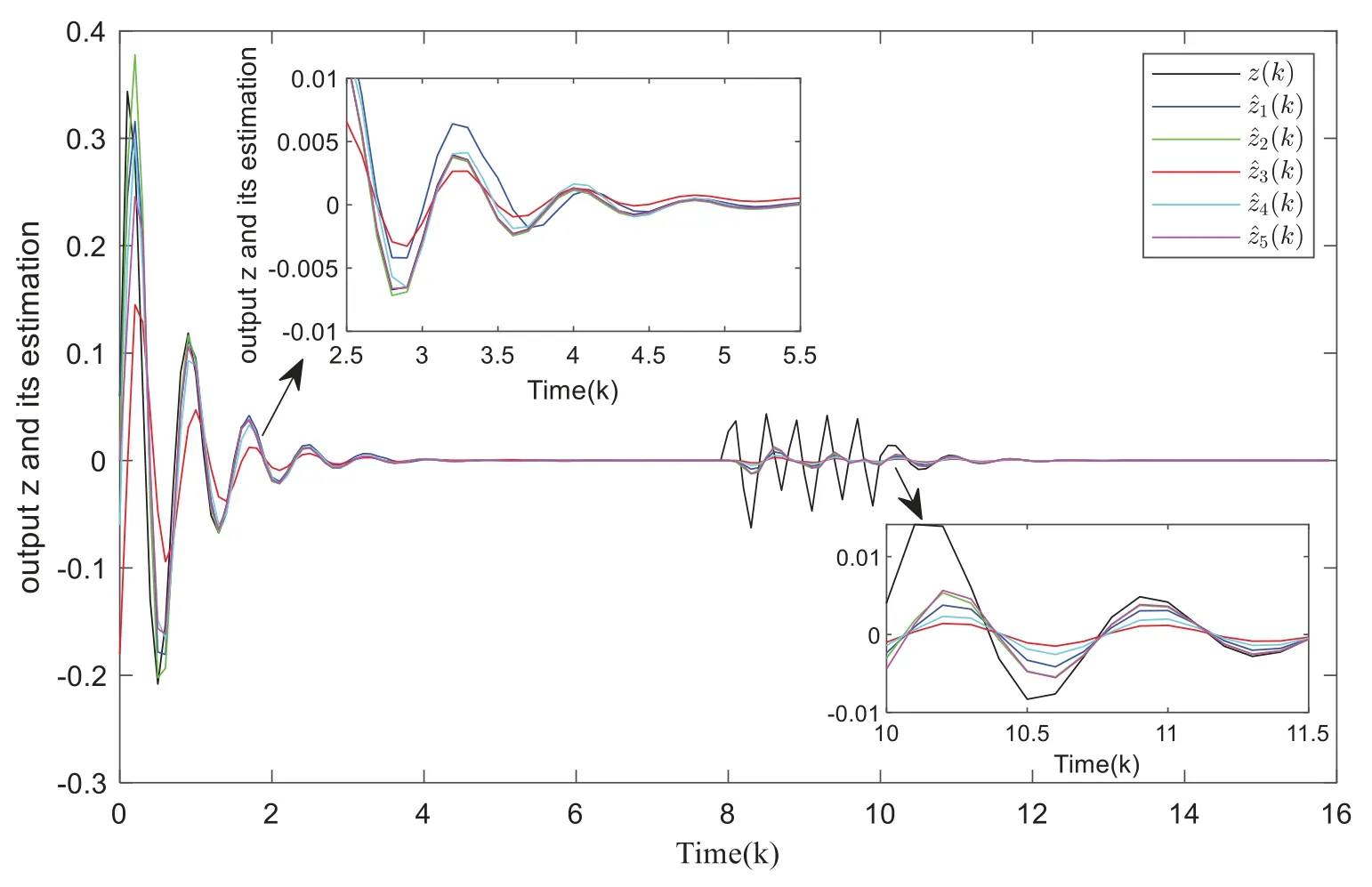
Figure 4:Plant output z(k)and its estimation

Fig.6 illustrates the self-triggered times of each filter.Under the periodic time-triggered mechanism,data transmits between the sensor and its neighbors at every sampling moment.It is clear that the self-triggered policy developed in this paper can effectively reduce the data transmission frequency within the network.In particular,in the first 6 time steps,filter 1-filter 5 is triggered less than 20 times under the self-triggered policy,while triggered 60 times under the time-triggered strategy.Therefore,the self-triggered policy developed in this paper can greatly save communication resources and computation burden of the filtering network.

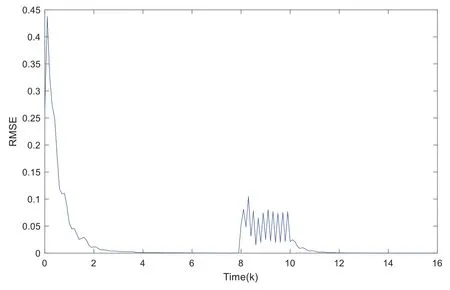
Figure 5:Filtering root mean square error

Figure 6:The self-triggered times of each filter

On the other hand,after the system is perturbed,the number of triggers intensively increases,and the triggers become gentle until the estimation becomes consensus during the time intervalk∈[8,14].This also means that filterishould update data released from neighbors frequently when the filtering departs from consistency.

In summary,the simulation results illustrate that the self-triggered policy can save communication and computation burden while satisfying filtering performance.

5 Conclusion

The self-triggering policy is developed for a class of distributed filtering systems in this paper.This policy can actively predict the time when the following exchanged data will be updated.Through such a policy,the frequency of data exchange can be reduced,while communication resources can be saved within the filtering network.Compared with the existing event-triggered communication scheme,this means that it is not necessary to continuously judge trigger conditions,which saves the computing burden.The asynchronous transmission problem caused by each filter node’s independent self-triggering can be solved by co-design.In order to make the research work close to the engineering practice,we will further consider transmission delay,packet loss,data conflicts,and other network induced phenomena.

Funding Statement:This work was jointly supported by the National Natural Science Foundation of China(Nos.61991402,62073154),the 111 Project(B12018),the Scientific Research Cooperation and High-Level Personnel Training Programs with New Zealand(1252011004200040).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.