非饱和矿堆溶液渗流迟滞与毛细扩散行为表征
2023-01-20王雷鸣李希雯尹升华周根茂刘培正邓博纳
王雷鸣,李希雯,尹升华,周根茂,李 辉,刘培正,邓博纳
1) 金属矿山高效开采与安全教育部重点实验室,北京 100083 2) 北京科技大学土木与资源工程学院,北京 100083 3) 金属矿山安全与健康国家重点实验室,马鞍山 243000 4) 武汉工程大学绿色化工过程教育部重点实验室,武汉 430205 5) 核工业北京化工冶金研究院,北京 101149
堆浸技术凭借其基建周期短、投入成本低、作业安全性高等优势,被广泛应用于低品位硫化铜矿、砂岩型金矿等战略矿产资源回采作业[1–2].其中,堆浸是一种气、固、液多相介质并存、渗流场、温度场、化学场等多场耦合的复杂反应体系[3];该体系中,溶液是可溶性氧、Cu2+/Cu+、Fe2+/Fe3+等有价金属离子等溶质赋存的重要媒介,直接影响着反应传质过程与浸矿效率[4].因此,能否有效表征堆内溶液毛细扩散、流动与分布规律是制约矿物浸出效率的重要因素.作为一种非饱和多孔介质中多相流,溶浸液的滞后现象是普遍存在且十分复杂的[5].已有研究发现堆内溶液流动主要有两种形式[6–7]:重力驱动的优势流和微观力驱动的毛细扩散流.其中,由毛细管力驱动的毛细扩散过程,对溶液渗流迟滞行为的影响是十分显著的[8].毛细扩散过程不仅是影响矿堆渗流迟滞行为,更重要的会影响传质过程与浸矿效率,需要深入理解和认识.
目前,针对非饱和堆内溶液渗流迟滞行为规律,特别是毛细扩散过程,国内外专家学者主要从物理实验、无损探测与数值模拟三个层面展开.其中,英国帝国理工大学Ilankoon等[9–10]开展矿堆溶液渗流迟滞实验,利用持液率、残余稳态持液率对非饱和矿石颗粒堆的持液行为进行了研究;王雷鸣等[11]立足于制粒矿堆,基于自主研发的持液行为原位监测系统实现了对不可动液、可动液的量化表征;毛细扩散过程对非饱和堆(如破碎矿堆、制粒矿堆等)持液行为的影响不可忽略[12],毛细入渗率与毛细速率、含水率呈正相关[13–14];随着多种无扰动探测设备技术的进步与引入,对溶液渗流的研究逐渐步入了微细观层面[15–16],英国剑桥大学Fagan等[17]利用核磁共振技术(Magnetic resonance imaging, MRI)对堆内溶液扩散和溶液优势流形成过程进行了研究,薛振林等[18]利用粒子图像测速技术(Particle image velocity, PIV)对矿堆结构内溶液渗流场进行了无损探测,有效实现了饱和溶液渗流场的可视化等.然而,单纯的实验研究与无扰动探测存在实验误差大、瞬态短时、随机性强等劣势,难以实现对溶液渗流过程进行有效的预测.对此,多类数学表征模型与渗流模拟软件逐渐被提出应用:国外 Bouffardt和 Dixon D G[19]、Liu和Hashemzadeh[20]合作研发了堆浸模拟程序HeapSIM,可以对工业堆浸喷淋、矿物浸出实现过程监测与结果预测;我国Wu[21]和尹升华等[22]利用COMSOL multiphysics软件和计算机断层扫描(Computed tomography, CT)构建非饱和矿堆网格模型并模拟了溶液渗流过程,证实了堆内优势流动区与溶液停滞区;此外,Ma等[23]、Zulian等[24]聚焦裂隙岩体渗流,利用Fluent开展了数值模拟研究,实现了破裂砂岩内的溶液流动规律.
综合已有研究不难发现,以往研究通常利用短时、瞬态可视化表征手段、数值模拟软件与相似物理渗流实验等方式开展研究,多聚焦溶液优势流动、重力流动、饱和条件、横向毛细扩散等方面[25–27],对非饱和矿堆体系的上向毛细渗流扩散、渗流迟滞行为的认识仍不深刻和不清晰,严重制约着浸矿过程中溶液渗流调控方法与措施,相关研究有待进一步深入开展.对此,加拿大Topp等提出了时域反射方法,该法利用电磁波在不同介质中的传播速度的差异来测定土壤含水率的一种方法,具有良好的可预测性[28–29],因此可以被有效借鉴到本研究当中.
对此,本文聚焦非饱和矿石颗粒堆,开展毛细溶液渗流迟滞与毛细扩散行为表征模拟,构建非饱和矿堆渗流模型,利用时域反射器(Time domain reflector)实时探测并计算非饱和矿堆内持液率,并结合Design expert进行响应曲面分析,深入探究非饱和矿堆内溶液渗流过程中各影响因素之间的相互关系.运用 COMSOL multiphysics开展溶液毛细渗透过程模拟,相关研究结果对调控矿堆内溶液渗流、强化溶液毛细扩散,进而提高矿物浸出效率具有良好的指导意义.
1 非饱和矿堆溶液渗流模型构建
1.1 基本假设
为研究溶液在浸出矿堆中的渗流规律,本文构建矿石颗粒堆简化模型,将其简化为矩形二维平面进行分析,建立尺寸为 0.05 m × 0.2 m 的数学模型.并且,做出如下基本假设:
(1) 矿石颗粒的骨架形状、颗粒相对位置不随时间发生变化;
(2) 颗粒间孔隙率大小、形状、连通性不随时间发生变化;
(3) 渗流过程中流体不可压缩;
(4) 矿石颗粒堆内孔隙率、渗透率各向同性;
(5) 矿石颗粒堆的孔隙空间中存在气液两相流动状态;
(6) 气液两相流动均为低速低扰动的达西渗流;
(7) 模拟环境温度不变.
1.2 控制方程
为探明矿堆非饱和浸出渗流规律,本文以界面作用为切入点,分析浸出液渗流毛细扩散状态[30].在矿堆渗透过程中,基于达西渗流定律、质量守恒定律和两相流理论[31],引入毛细吸力和体积含水率的变量,分别推导矿堆非饱和渗流过程中液相和气相的运移方程,如式(1)和(2)所示:

式中:C为容水度,反映了非饱和多孔介质的储存特性,Cw和Ca分别为液相和气相容水度;pw和pa分别 为孔隙水压力和孔隙气压力;ρw和ρa分别为液相和气相的密度,kg·m−3,κ为饱和渗透率,%;kr,w和kr,a分别为液相和气相的相对渗透率,%;η为运动黏度,Pa·s;g为重力加速度,m·s–2;D为垂直坐标.
目前,矿堆水分特征曲线目前具有代表性的模型较多,运用较为广泛的模型是非饱和渗流van Genuchten-Mualem(VGM)模型[32],为求解函数毛细压力Pc,根据持液率和渗透率关系,分别定义θ、C、Se和kr,如式(3)~(6)所示:

式中,Se为饱和度,1;Hc为毛细压力水头,m;θw为持液率,%;其中,θw的变化范围从残余持液率θr增大到饱和持液率θs.α,n,m和L是 Van Genuchten参数,由固相介质本身决定.
迭代后,可求得气相的VGM公式:

1.3 物理模型及网格划分
为探明矿堆非饱和浸出渗流过程中毛细上升规律,定义模型为经过对称轴的任意截面.模型的宽为 5 cm,高为 20 cm;设置矿堆底存在高 3 cm、水平方向无穷大的恒定饱和流动区.
利 用 COMSOL multiphysics 5.0 数 值 模 拟 软件,构建二维网格模型,如图1所示.由图1可见,较矿堆中部而言,矿堆顶部和底部的边界网格结构更为细密,其可更好的表征溶液毛细扩散规律.
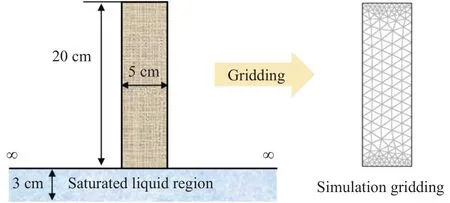
图1 柱浸颗粒堆物理模型构建及网格划分Fig.1 Physical model and mesh of the packed heap in column leaching
借鉴工业矿堆渗流的实际情况及相关文献数据,选取模型主要参数,如表1所示.
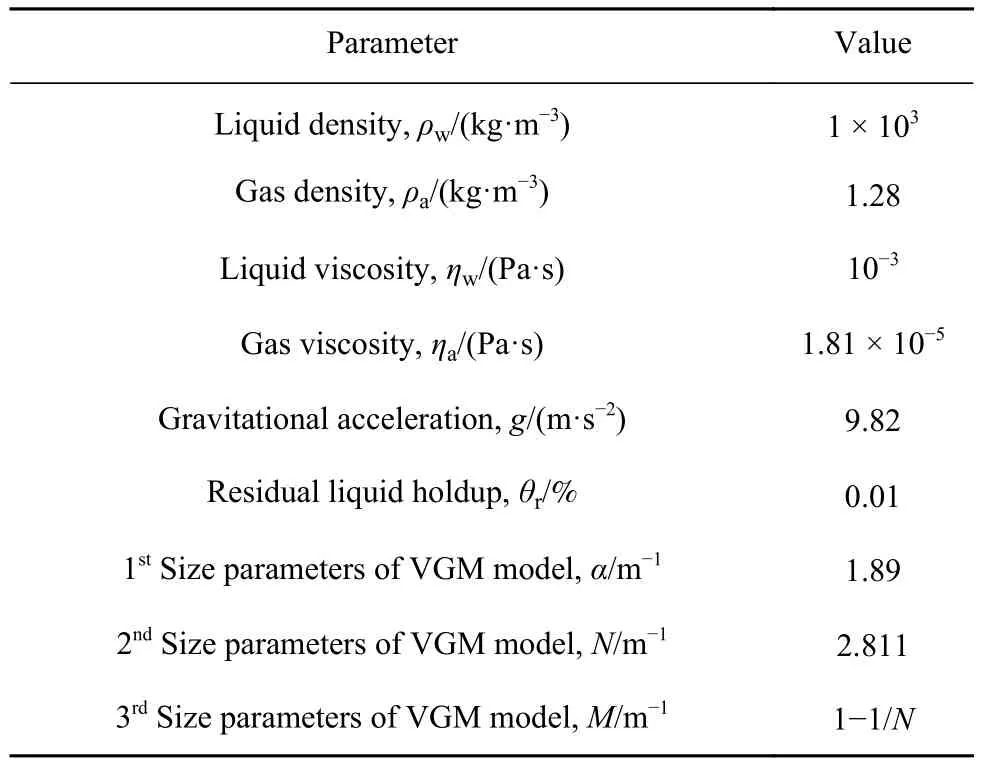
表1 数学模型的关键参数Table 1 Key parameters of the mathematical model
1.4 边界条件
建模前对模型边界条件进行设定.初始状态,矿堆中的气液是符合静压分布的.而液相从底部向上运动,气相是在矿堆顶部出现,且不会消失.假定气液两相流动均为低速低扰动的达西渗流,在入口处、表面、边壁,气液两相满足式(11).
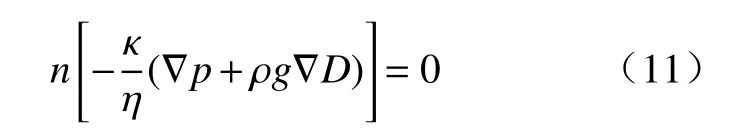
在底部,液相和气相的压力为恒压,如式(12)所示:

式中,p为液体t时的总压强,p0液面上方的压强,t为时间.
1.5 数值模拟方案与赋值
为进一步探究溶液在浸出矿堆内的溶液渗流迟滞规律,将物理实验结果和数值模拟相结合,利用孔隙率对渗透系数进行赋值,考察不同孔隙率、喷淋强度对非饱和矿堆渗流过程;探索渗流速度、毛细吸力、持液率、非饱和系数等相关特性.具体模拟和实验方案,如表2和表3所示.
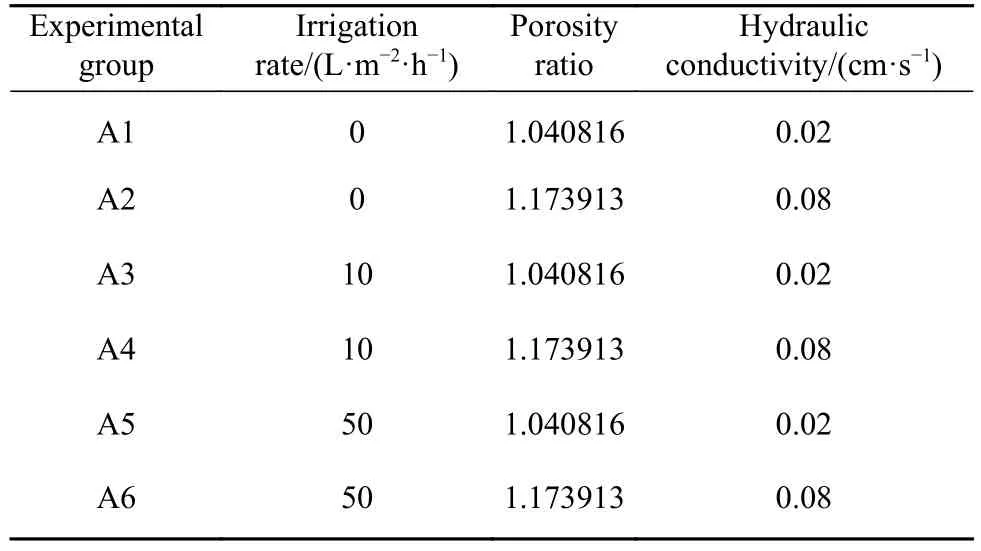
表2 不同喷淋强度和孔隙率条件下溶液毛细渗流模拟方案Table 2 Experimental scheme of the liquid capillarity seepage under different irrigation rate and porosity condition
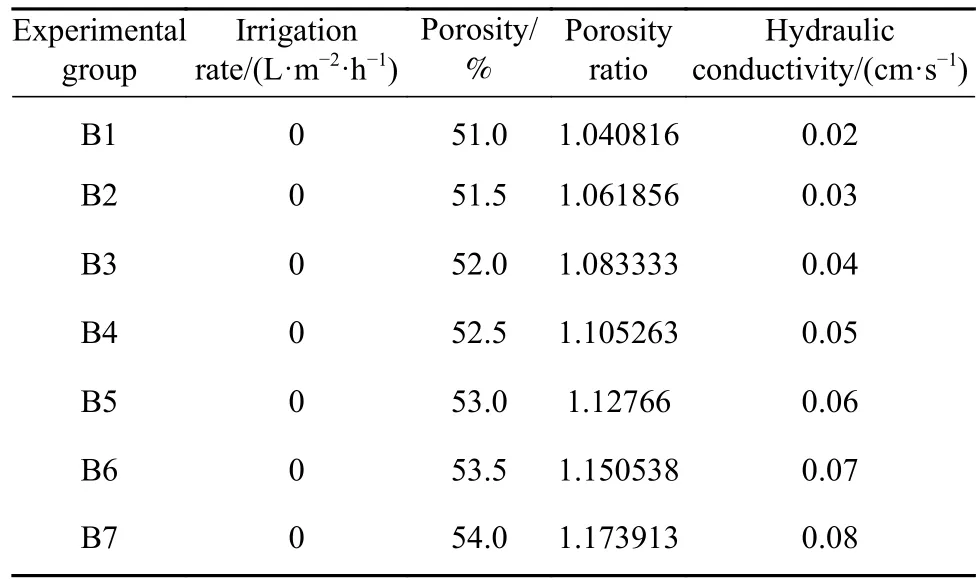
表3 不同孔隙率条件下溶液毛细渗流模拟方案Table 3 Experimental scheme of the liquid capillarity seepage under different porosity condition
依据初始实验条件差异,各组互为对照,对实验方案进行简要阐释,如下:(1)不同喷淋强度与孔隙率条件下,共设置6个实验组,喷淋强度分3 个阶梯,即:0、10、50 L·m–2·h–1,矿石颗粒堆孔隙结构用孔隙比进行表征,选择2种,即:1.04、1.17.(2)不同孔隙率条件下,不进行喷淋作业,即仅依赖毛细吸力和下部饱和溶液区供给颗粒堆,孔隙比介于1.04~1.17,孔隙率介于51%~54%,相应地,矿石颗粒堆的水力传导系数介于0.02~0.08 cm·s–1.
2 非饱和堆溶液毛细渗流物理实验
流体在毛细管中流动时,由于各相的张力不同,相界面会产生毛细管吸力,毛细上升过程的实质是气液两相流的过程.为进一步揭示非饱和堆溶液毛细渗流规律,利用时域反射器(Time domain reflector, TDR),基于式(13),对非饱和堆内持液率(或称含水率)进行原位实时探测和计算,揭示不同喷淋强度、孔隙比等条件下非饱和堆溶液毛细渗流实验.

式中,θTDR为校正的持液率,%;为平均持液率,%;θ1~4为4个测量点位的持液率,%.溶液渗流物理实验装置,如图2所示.该毛细渗流实验研究装置是由喷淋系统(1)、柱体(2)、非饱和矿堆(3)、恒液位槽(4)、多孔隔筛(5)、支撑结构(6)、TDR(7)、数显系统(8)、溢流口(9)、集液罐(10)共10部分组成.实验开始前,将非饱和矿石堆的底部浸泡在恒定液面的溶液区域,使之在矿堆最底部形成一个饱和溶液区.实验开始后,溶液在毛细吸力作用下,溶液自下而上发生毛细扩散,形成浸润面,并不断向上迁移扩散,随着堆内溶液毛细扩散过程趋于停滞,非饱和矿石颗粒堆逐步达到稳态持液.该过程中,利用毛细吸力等关键参数,实现溶液毛细扩散过程的有效监测.
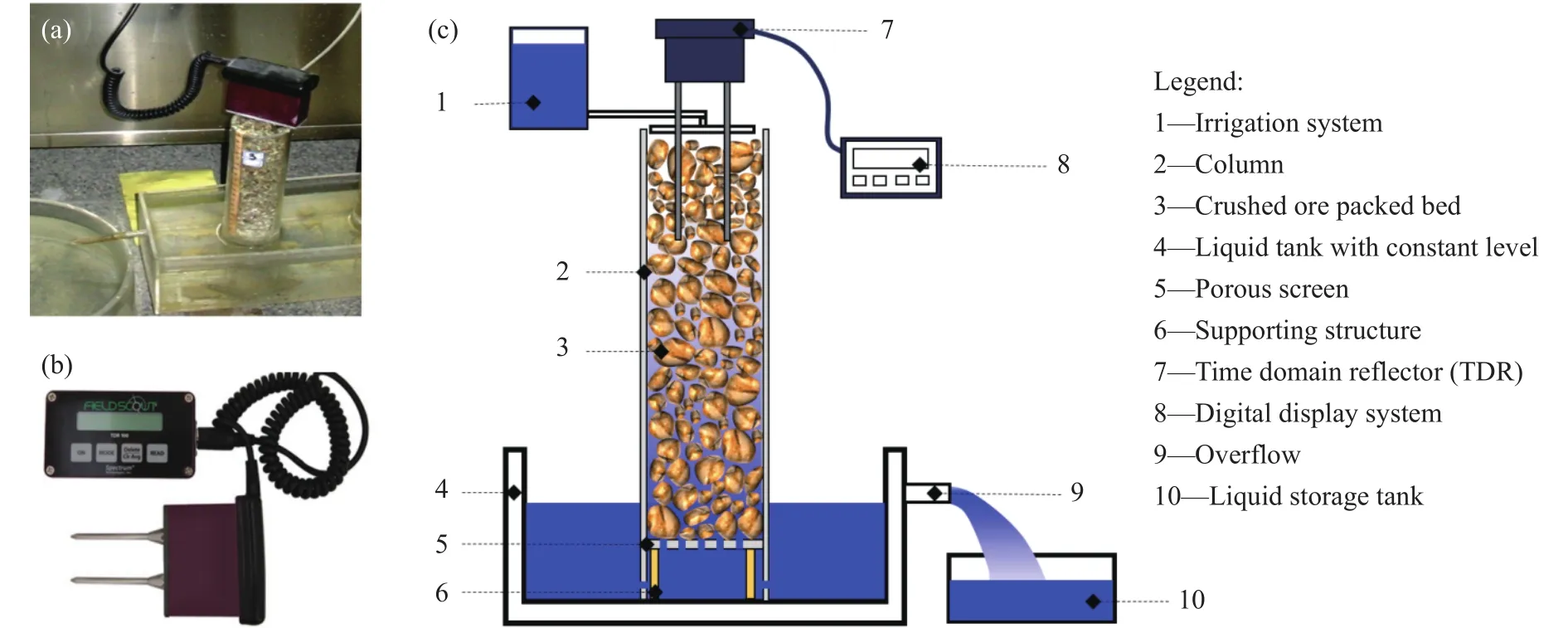
图2 非饱和矿堆溶液毛细上升实验装置构成.(a)毛细扩散实验实物图; (b)时域反射仪; (c)实验装置结构构成Fig.2 Composition of the experimental device for the capillary rise of the unsaturated ore pile solution: (a) macroscale image of the capillary diffusion experiment; (b) time-domain reflector; (c) detailed structure of the experimental device
3 结果与讨论
3.1 持液率随浸润时间变化规律
持液率是非饱和渗流中最具代表性的参数之一,探明持液率变化是揭示非饱和矿堆内部渗流迟滞行为规律的重要前提.其中,喷淋强度和矿石粒径均对矿堆持液率有重要影响[33–34].对此,本文取图1模型顶部中点为研究对象,坐标为(0.025,0.2),基于前述构建的毛细扩散数学模型,开展对液体流动过程中持液率变化过程数值模拟,生成不同孔隙比和喷淋强度条件下非饱和堆内持液率曲线,如图3所示.
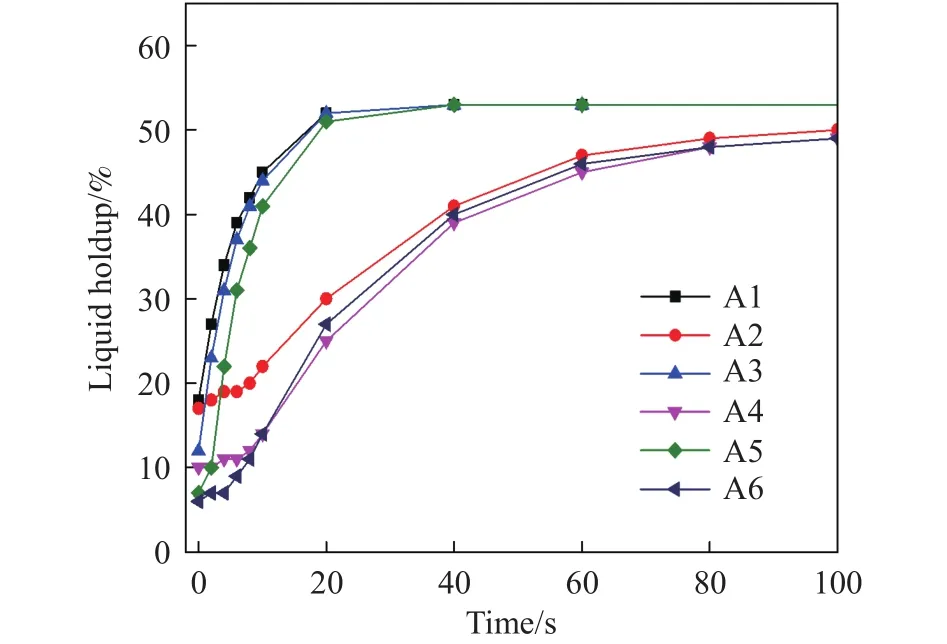
图3 不同喷淋强度和孔隙比条件下持液率随时间变化Fig.3 Changes of the liquid holdup with time under different irrigation and porosity ratio conditions
结果表明,随着溶液喷淋作业的进行,矿堆持液率的收敛性逐渐增加.矿堆持液率与破碎矿石颗粒的几何平均粒径呈负相关、与孔隙率呈正相关、与喷淋强度呈正相关.由图3可知:(1)对比A1-A2、A3-A4和A5-A6可知,不考虑溶液喷淋强度影响时,矿堆持液率与孔隙比、水力传导系数呈正相关;以t= 20 s为例,具有更高孔隙比(1.174)和水力传导系数(0.08 cm·s–1)的 A2 组持液率(约为 52%)明显高于 A1组持液率(约为 30%).(2)对比A1-A3-A5、A2-A4-A6可知,不考虑水力传导系数和孔隙比的影响时,矿堆持液率与喷淋强度呈正相关;以t= 10 s为例,具有更高喷淋强度的 A1组持液率(45%)要高于A3组持液率(44%)和A5组持液率(41%).并且,在喷淋初期(0~20 s),上述因素(喷淋强度、水力传导系数和孔隙比)对矿堆持液率的影响更为显著.
分析认为:矿石颗粒堆持液率对矿石粒径(孔隙率)的敏感度要明显高于对喷淋强度的敏感度;矿石粒径越大,溶液喷淋强度对矿堆含水率的影响越小[35].在相同孔隙比条件下,喷淋强度小的模型持液率在初期增长缓慢、后期增速较快.结果表明:在溶液喷淋初期颗粒堆内毛细吸力极高,喷淋溶液可以自下部饱和溶液区发生上向位移,形成浸润锋,快速进入颗粒堆内部,此时,固–液接触主要以润湿作用为主.当喷淋强度越小时,模型内部的溶液量较少,宏观表现为持液率较低;反之,喷淋强度较大时,宏观矿堆持液率较高.在溶液喷淋后期,堆内原有颗粒间、颗粒内孔隙被溶液大量填充,重力场和渗流场共同影响溶液毛细渗流过程[36],堆内溶液量趋于稳态,宏观表现为持液率增速减慢.
3.2 堆内不同位置处毛细吸力与持液率关联规律
忽略顶部喷淋作用的影响,本文探究了不同孔隙率条件下矿石颗粒堆毛细渗透行为规律,获取毛细吸力–持液率特征曲线,结果如图4所示.由图4可见,在相同孔隙结构(孔隙率)条件下,矿堆顶部的毛细吸力要明显高于矿堆底部的毛细吸力,这种毛细吸力的差异在物理模型的中部位置更为显著.这是由于矿石颗粒堆底部与饱和溶液接触,该处的持液率最大且毛细吸力最小.以孔隙率52.0%为例,矿堆底部稳态毛细吸力约为1669.5 Pa,明显高于矿堆顶部的稳态毛细吸力(139.0 Pa).
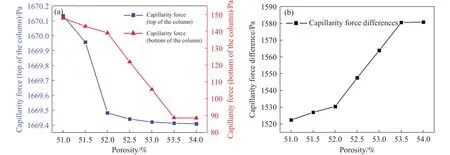
图4 非饱和堆毛细吸力特征–孔隙率关联关系.(a) 堆顶毛细吸力与孔隙率间的关系; (b) 毛细吸力差值与孔隙率间的关系Fig.4 Relationship of capillarity suction features and porosity of ore heap: (a) relationship between capillarity force (top of the column) and porosity;(b) relationship between capillarity force differences and porosity
无论是颗粒堆顶部还是底部,毛细吸力均与孔隙率的变化呈负相关,即:矿堆该处的毛细吸力随孔隙率的增加而减少.以矿堆顶部为例,当矿堆孔隙率由51%增加至52.5%时,堆顶毛细吸力由1670.1 Pa 下降至 1669.4 Pa.此外,堆顶的毛细吸力变化程度明显大于堆底.由图4(a)可见,对比孔隙率为51%和54%的矿堆,可见二者堆底毛细吸力的净差值为59.189 Pa,明显高于堆顶毛细吸力的净差值(0.725 Pa).分析认为:液体总是从吸力小往吸力大的方向运动,模型顶部和底部的毛细吸力之差的物理意义为液相自下而上的运动的驱动力[37],毛细吸力克服重力和摩擦阻力做功并趋于平衡.图4(b)表明,溶液上升过程中,由于孔隙率较大、持液率差较大,液体自下而上的运动的驱动力也就越大.虽然孔隙率越大,矿堆中的毛细驱动力越大,但由于液体自重和摩擦阻力的共同作用,溶液上升速度反而越小.结合已有研究与工业现场运行情况可知,这种溶液的渗流迟滞行为对于矿石颗粒润湿和矿堆持液率的影响是十分明显的,矿堆矿石内孔隙结构的发育程度越高,矿堆内的溶液渗流迟滞行为越显著,矿石颗粒的润湿效果更好.
3.3 矿石–溶液特征曲线
假定矿石颗粒堆内孔隙与大气联通,且不考虑摩擦阻力和蒸发作用,那么可知:矿石颗粒堆内压力水头与毛细水头的值大小相等但方向相反.基于此假设,本文取模型顶部中点为研究对象,绘制矿石颗粒堆持液率–水头压力(蓝线)和毛细吸力(红线)关系曲线,如图5所示.
由图5可知,在相同持液率条件下,压力水头与毛细水头的对称特征被有效的证实.随着喷淋时间的增长,非饱和矿石颗粒堆持液率的收敛性增加.对于孔隙比小的矿堆,需要更长的时间达到稳态持液.对于孔隙比相同条件时,喷淋强度主要影响初期持液率的值;喷淋强度越大,初期持液率增长越快.当持液率为0%时,毛细吸力水头达到峰值,约为2×104Pa;随着矿堆内溶液量的逐渐增加,持液率明显上升,相应地,堆内毛细吸力逐渐减小.当矿石颗粒堆持液率达到稳态持液率时,堆内毛细吸力下降至0 Pa.对比不同喷淋强度和孔隙比条件下持液行为差异可知,当持液率相同条件下,矿堆孔隙较为发育时毛细吸力较小;换言之,毛细吸力的变化对孔隙率较小矿石颗粒堆更敏感.
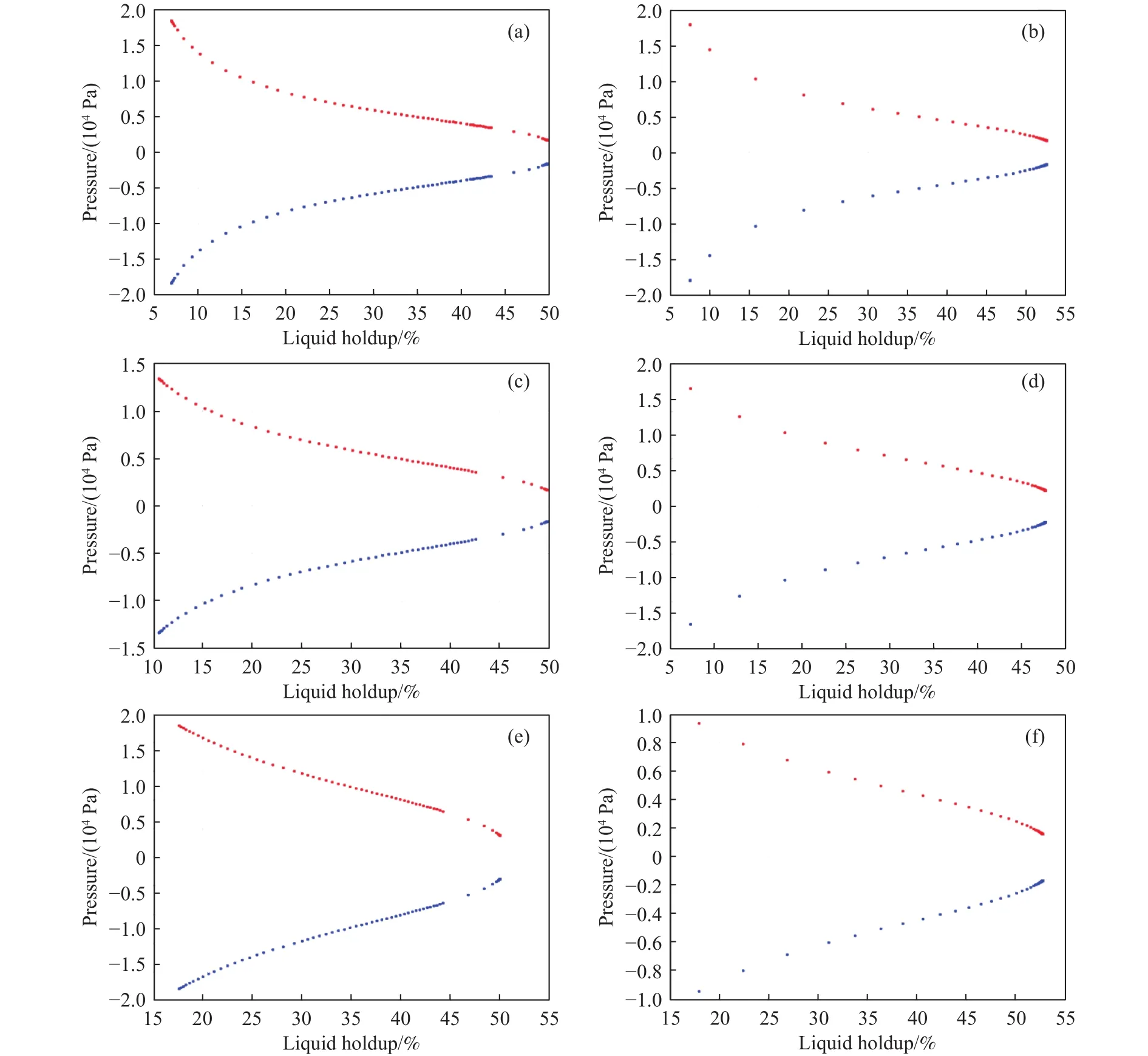
图5 持液率与水头压力(蓝线)和毛细吸力(红线)关系.(a)A1 组;(b)A2 组;(c)A3 组;(b)A4 组;(c)A5 组;(b)A6 组Fig.5 Relationship of the liquid holdup and the pressure heap (blue) and capillarity suction (red): (a) A1 group; (b) A2 group; (c) A3 group; (d) A4 group: (e) A5 group; (f) A6 group
3.4 非饱和堆内毛细吸力、孔隙比与喷淋强度响应规律
为进一步探讨堆内毛细吸力、孔隙比和喷淋强度间的关联响应规律,利用Design expert进行响应曲面分析.当t= 400 s时,堆内毛细渗透过程达到稳态,用模拟软件计算不同喷淋强度和孔隙率条件下的毛细吸力,分别获得顶部毛细吸力、底部毛细吸力、毛细吸力差与孔隙比和喷淋强度的响应规律,如图6所示.
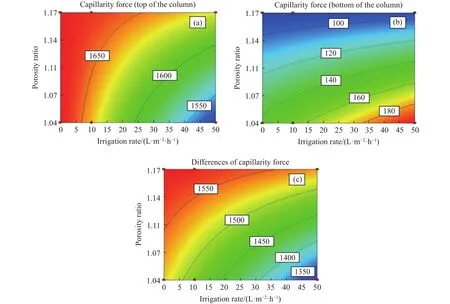
图6 毛细吸力对喷淋强度和孔隙率的等值面特征.(a) 堆顶; (b) 堆底; (c) 毛细吸力差值Fig.6 Equivalent surface characterization of the capillarity suction to the irrigation intensity and porosity: (a) top of column; (b) bottom of column; (c)differences of capillarity force
结果表明:喷淋强度、孔隙比和毛细力间存在明显的响应关联关系,喷淋强度较小时,顶部毛细吸力的值基本上不会随孔隙率发生变化.数值模型底部的毛细吸力受喷淋强度和孔隙比的影响较为明显.当喷淋强度越大(50 L·m–2·h–1)时,孔隙比越小(1.04),底部毛细吸力越大;反之,当喷淋强度越小(10 L·m–2·h–1),孔隙比越大(1.17)时,自下而上的毛细吸力越大,也越不利于内部液体的渗透扩散.
为进一步考察堆内渗透特征与毛细吸力间的内在关联,本文利用构建的溶液毛细渗流模型与COMSOL multiphysics数值模拟软件,获取了沿模型垂直方向的相对渗透率分布规律,由图7所示.
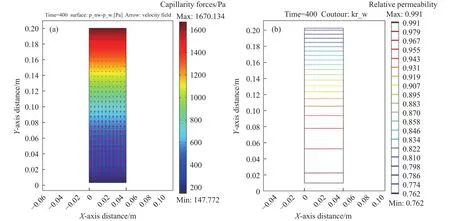
图7 基于 COMSOL multiphysics 的矿堆内毛细吸力稳态分布特征.(a) 毛细吸力; (b) 相对渗透率Fig.7 Steady distribution characterization of the capillarity suction in the ore heap relied on COMSOL Multiphysics: (a) capillarity forces; (b) relative permeability
结果表明:相对渗透率kr随着高度的增加呈现非线性递减特征,随高度增加,kr加速减小,在模型顶部达到最小值.表明矿堆达到稳态持液时,矿堆上部的渗透率低,下部的渗透率高.矿石颗粒堆的渗透特性主要由顶部渗透率决定的.结合矿堆稳态毛细吸力、相对渗透系数的计算结果发现:在孔隙率越小和喷淋强度较大时,矿堆更易达到稳态持液状态,并且,底部毛细吸力越大、相对渗透率越大.在毛细吸力驱动下,矿石颗粒堆持液率逐步上升达到稳态持液率.矿堆内溶液渗流扩散过程受重力和毛细吸力共同作用,两者方向相反.孔隙率较大时,毛细吸力较大但渗透较好,总体表现为浸润面扩散过程较慢.堆内溶液毛细上升速度分布不均匀,具体表现为:矿堆顶部毛细上升速度较慢,矿堆下部毛细上升较快.
4 结论
本次建模主要基于矿堆达西渗流和两相流模型,借助多相多场模拟软件COMSOL multiphysics的多物理场功能,模拟验证矿堆非饱和渗流过程,获得非饱和矿堆内持液率、毛细吸力、孔隙率、喷淋强度等之间的相互联系.通过模拟分析,得出以下结论:
(1) 相较于喷淋强度,矿堆持液率对堆孔隙率更为敏感,矿堆持液率随喷淋时间的增长收敛性增加,且孔隙率小矿堆需要更长时间达到稳态持液;
(2) 毛细吸力的变化对孔隙率较小的矿石颗粒堆更敏感.矿堆底部毛细吸力最小、顶部最大,且孔隙率越大两端的压力差越大、内部溶液毛细上升速度越慢,利于溶浸液渗透;
(3) 喷淋强度较小时,孔隙比越大,毛细吸力越大,但此时重力对溶液渗流影响较大,不利于堆内溶液的渗透扩散;在喷淋强度较大时,孔隙比越小,底部毛细吸力越大,毛细吸力的影响提升,矿堆更易达到稳态持液状态.
