两种算法用于预测A2/O工艺脱氮条件

肖 飞，康增彦，王维红

(1.新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052，2.塔里木大学 水利与建筑工程学院，新疆 阿拉尔 843300；3.中建三局安装工程有限公司，湖北 武汉 430079)

随着城市化的快速发展，水污染日益严重，水资源问题已成为全球关注的焦点[1-2]。因此，污水再生回用和良性循环已成为我国改善水环境的战略举措，如大力兴建污水处理厂。目前，我国城市污水处理厂大多采用生物法进行处理，其工艺主要包括氧化沟工艺、SBR工艺[3-4]、A/O工艺以及A2/O工艺[5]等，其实质是利用活性污泥中的微生物对污水中的有机污染物进行生物降解，达到去除污水中有机污染物的目的。以应用最为广泛的A2/O工艺为例，该工艺在降解高浓度制药废水[6]、印染废水[7]、焦化废水[8]和应用在寒冷地区[9]均取得优异的效果。然而，在A2/O工艺的二级处理部分存在释磷、硝化、反硝化和吸磷等反应过程，因此只有协调好各个过程，才能保证处理后的水质达到《城镇污水处理厂污染物排放标准》(GB 18918—2002)一级标准的A标准。

基于此，本文以新疆某污水处理厂(改进A2/O工艺)为研究对象，选取碳氮比(C/N)、碳磷比(C/P)和有机负荷(F/M)作为工艺条件。在单因素试验基础上，分别利用RSM-BP技术和ANN技术建立优化条件与总氮(TN)去除率之间的预测模型，以期为污水处理工艺的实际运行提供理论指导。

1 材料与方法

1.1 头屯河区污水处理厂工艺概况

头屯河区污水处理厂位于乌鲁木齐市经济技术开发区，主要负责乌鲁木齐市头屯河合作区、工业园区及三坪农场场部生活污水和工业废水的处理，其中工业废水占25%～30%，生活污水约占70%。污水处理厂Ⅰ期2003年7月投入运营，工艺为水解酸化-改进SBR法，排放标准执行《城镇污水处理厂污染物排放标准》(GB 18918—2002)一级B标准。2019年进行提标改造，Ⅱ期工艺为水解酸化+A2/O工艺，执行《城镇污水处理厂污染物排放标准》(GB 18918—2002)一级A标准，设计来水水量为3×104m3/d，进水水质为生化需氧量(BOD)600 mg/L，TN 100 mg/L，TP 10 mg/L，NH3-N 70 mg/L；实际运行时COD 500～750 mg/L，BOD 100～200 mg/L，TP 5.5～25 mg/L，TN 28～140 mg/L，污泥质量浓度(MLSS)3 500～6 000 mg/L，DO控制在0.9～4 mg/L，污泥负荷为0.11 kg/(m3·d)，MLVSS/MLSS(混合液挥发性悬浮固体浓度与悬浮固体浓度比值)为0.69，水温10～25 ℃。其他基本工艺参数见表1。

表1 污水处理厂Ⅰ期和Ⅱ期基本工艺参数Tab. 1 Sewage treatment plant phase I and phase II process basic process parameter

1.2 样本来源及处理

试验样本取自2019年头屯河污水处理厂。水质取样点分别为A2/O工艺的厌氧段、缺氧段和好氧段，即污水处理设施的入口和总排放口，每隔4 h取一次样，用水桶取样，存储水样容器为硼硅玻璃，容积100 mL，-18～-22 ℃储存备用。

1.3 水质分析方法

1.4 方法

1.4.1 单因素试验

取2019年3月进水作为试验数据，在污水处理厂共获得270组数据集进行试验。同时，利用该数据集分别考察C/N、C/P和F/M对TN去除的影响。参数考察范围分别为：C/N为3～15，C/P为30～130，F/M为0.04～0.17 d-1。试验时，固定好氧池HRT为5.5 h，SRT为15 d，R为50%，r为200%，从得到的数据集中选取相似工况的运行数据，至少选择3组，以3次TN平均值作为最终值。首先，当C/P=70，F/M=0.09 d-1时，改变C/N分别为6.00、7.50、9.00、10.50、12.00；同理，当C/N=9.00，F/M=0.09 d-1时，改变C/P分别为50、60、70、80、90；当C/N=9.00，C/P=70时，改变F/M分别为0.07、0.09、0.11 d-1。

1.4.2 RSM试验设计

基于单因素试验，采用Box-Behnken设计原理进行RSM试验，以C/N、C/P和F/M为条件，TN去除率为响应值，进一步优化TN去除的最佳条件。

1.4.3 ANN模型构建

采用3-X-2神经网络创建试验因素的优化模型。选取C/N、C/P和F/M作为网络3个输入神经元，TN去除率和剩余量作为输出层节点。其中学习率取值为0.01～0.50，动态常数取值为0.10～0.80。隐含层神经元节点数由式(1)计算可得，归一化处理为[0，1]，归一化公式见式(2)。

(1)

式中：p为输入层节点神经元数；q为输出层节点神经元数；c为经验值(1≤c≤10)。

(2)

式中：fi为第i个输入样本空间的训练样本值；f′i为fi归一化后的数据，f′i∈[a，b]；a和b为初始网络节点的权值和阈值；fimax为第i个输入样本空间中训练样本的最大值；fimin为第i个输入样本空间中训练样本的最小值。

1.4.4 数据处理

采用Design Expert 10.0软件进行RSM分析；Matlab 2015构建RSM-BP和GA-NN模型；Origin 2017制作数据绘图。

2 结果与分析

2.1 单因素试验结果

2.1.1 不同进水C/N对缺氧池中TN去除率/量的影响

图1 进水C/N比对缺氧池中TN去除率/量的影响Fig. 1 Effect of C/N ratio of influent on TN removal rate/amount in anoxic pools

表2 的指标跟踪监测(C/N=10.5)Tab. 2 index tracking monitoring(C/N=10.5)

图2 进水C/P对NH3-N和TN去除率及浓度的影响Fig. 2 Effect of C/P ratio of influent on NH3-N and TN removal rate and concentration

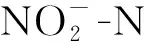
图3 进水F/M对缺氧池中和TN去除率的影响Fig. 3 Effect of influent F/M on and TN removal rates in anoxic pools

图4 进水F/M对好氧池中和NH3-N去除率的影响Fig. 4 Effect of influent F/M on the removal rate of and NH3-N in aerobic tank

从图4(b)可以看出，F/M为0.07～0.16 d-1时，NH3-N去除率最高，平均可高达89.91%，其中F/M为0.09 d-1时，NH3-N去除率为95.68%，达到峰值，此时系统的反硝化性能最强；另外，由NH3-N的物料守恒可知，NH3-N的去除不光靠反硝化菌的反硝化作用，还与微生物的同化作用密切相关(F/M处于合理水平)。

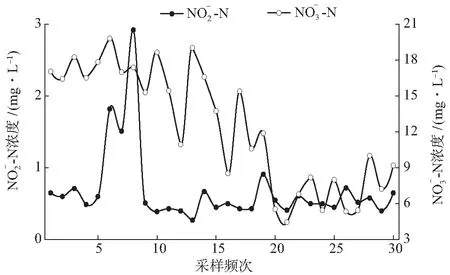
图5 进水F/M对好氧池中和浓度的影响Fig. 5 Effects of influent F/M on concentrations in aerobic tanks

综合以上单因素结果，选择F/M为0.07、0.09和0.11 d-1进行响应面实验。

2.2 响应面优化试验设计及结果

2.2.1 响应面试验设计

运用Design Expert 10.0中Box-Behnken模式设计实验方案，取得17个试验点，试验设计和结果如表3所示。3个变量中，设C/N为X1，C/P为X2，F/M为X3。

表3 Box-Behnken 试验设计表及结果Tab. 3 Design and results of Box-Behnken experiments

2.2.2 以TN去除率和去除量为响应值的响应面结果分析

2.2.2.1 回归方程的建立与方差分析

采用辅助模型Quadratic进行分析，得到TN去除率和去除量的二次回归预测方程，如式(3)和(4)所示。

(3)

(4)

2.2.2.2 响应面结果分析

RSM的等高线分布图和3D图能够直观反映变量交互作用对响应值的显著性。图6为不同因素对TN去除率的响应面图。由图6可知，不同交互因素之间均存在稳定的极值，交互因素C/N、C/P的等高线呈现圆形(椭圆离心率为1)，且响应曲面图坡度较陡，表明所对应的因素之间的交互作用极为明显，而交互因素C/N、F/M和C/P、F/M的等高线呈现椭圆，交互作用较显著。

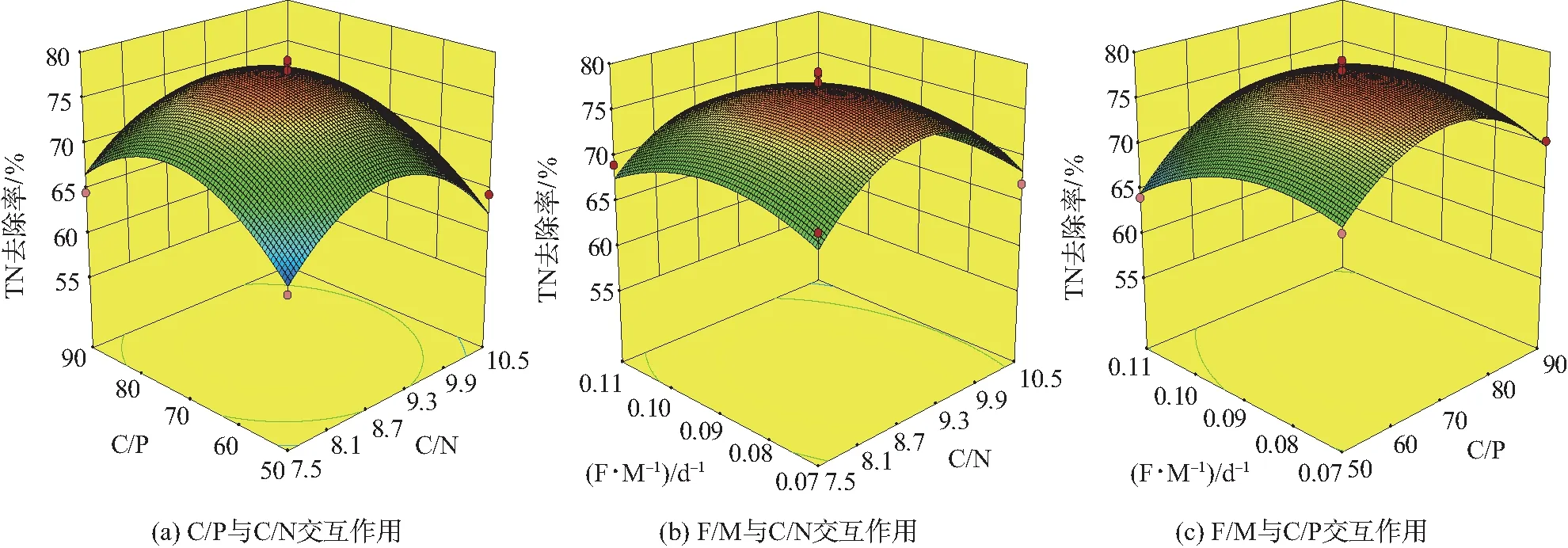
图6 各试验因素交互作用的响应面和等高线Fig. 6 Response surface and contour plot of the interaction of various test factors

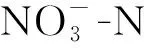
2.2.2.3 响应面优化结果

经RSM软件分析得出TN去除率的最佳工艺为：C/N=8.91、C/P=71.48和F/M=0.086 d-1，在此条件下TN去除率预测值为75.94%，去除量为53.59 mg/L。

2.3 ANN模型构建结果

2.3.1 ANN结构

ANN模型以C/N、C/P、F/M作为网络的3个输入神经元，中间有8个隐含层，包括5个神经节点。确定ANN的网络拓扑结构为3-8-2，对该结构进行训练优化，训练过程中各参数设置为：训练循环次数50 000，学习率0.05，训练误差目标0.001；调整学习率和误差目标分别为0.01和0.000 1。

2.3.2 RSM-BP神经网络模型的训练

以RSM结果及67组虚拟数集作为训练样本，执行ANN模型的拟合迭代过程[30]，如图7所示。通过将ANN模型与RSM数据集结合，训练次数至第11步时，模型性能达到所设定的均方误差(mse)目标要求，mse为10，最佳验证性能为13.62。经RSM-BP拟合的最大预测值为76.40%，对应的工艺条件为：C/N=8.95、C/P=72.01和F/M=0.088 d-1；修正后为：C/N=9.00、C/P=72.00和F/M=0.09 d-1，TN去除率为79.12%，去除量为55.34 mg/L。对TN去除率输出值与目标值进行回归分析，回归系数R2分别为0.95、0.99、0.93、0.95，综合回归系数为0.957，说明8层神经模型具有较高的精确度和很强的预测能力。

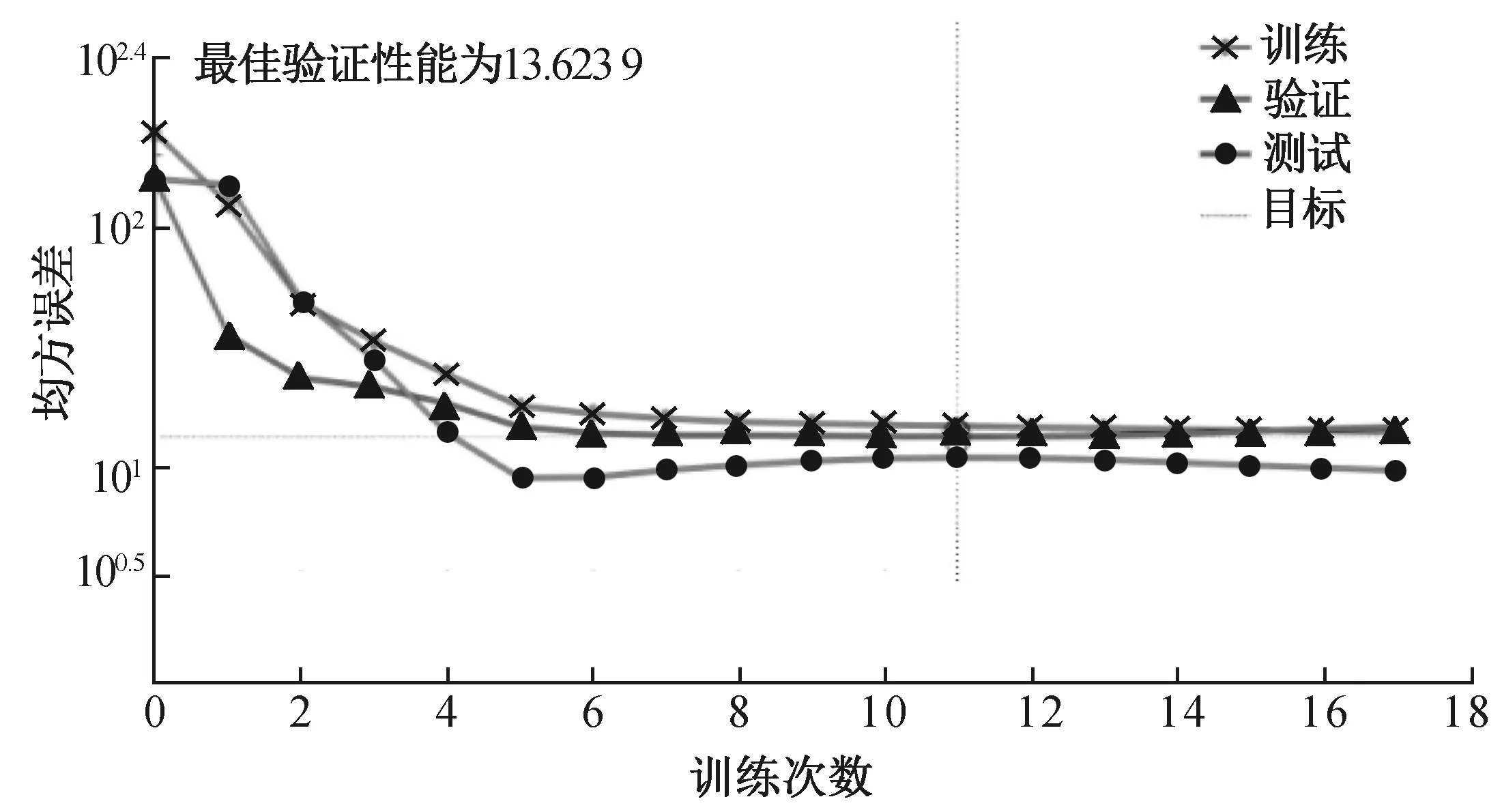
图7 TN去除率的BP模型训练过程Fig. 7 BP model training process of TN removal rate

RSM和RSM-BP预测值的比较见表4。通过比较两组的相对误差值发现，在17组实验中，RSM-BP神经网络预测的准确性有12组高于RSM分析方法。与试验真实值相比，RSM和RSM-BP网络测得的TN去除率的平均绝对误差分别为1.45、0.98，TN去除量的平均绝对误差分别为0.65、0.24，同时RSM-BP比RSM预测值的相对误差更小。总体来说，RSM-BP预测模型优于RSM预测模型。

表4 RSM和RSM-BP的相对误差值Tab. 4 Relative error values of RSM and ANN

2.3.3 GA-NN神经网络模型的训练

将ANN和GA结合对TN去除率全局寻优[31]，获得最佳TN去除率的工艺条件，迭代过程中的最优适应度值如图8所示。由图8可以看出，GA-NN算法经过39次迭代，TN去除率达到最佳适应度值，去除率为79.25%，去除量为56.78 mg/L，最优工艺参数为：C/N=9.00、C/P=72.15、F/M=0.09 d-1。

图8 GA-NN算法收敛过程Fig. 8 GA-NN algorithm convergence process

2.3.4 RSM-BP与GA-NN预测结果对比

择优选取RSM-BP和GA-NN这2种方法得出的最佳工艺参数进行比较，分别在2种条件下进行3次验证实验，取平均值，结果如表5所示。通过实验结果可以得出，GA-NN算法优化出的最佳工艺条件下的TN去除率为79.25%，高于RSM-BP算法的79.12%，且GA-NN算法相对误差值也远低于RSM-BP算法；GA-NN算法优化得到的结果值与实验值更接近，二者之差仅为0.24%；GA-NN算法在最佳参数下的TN去除率较实验值稍高，准确度优于RSM-BP算法，但TN去除量的准确度低于RSM-BP算法。产生这一现象的原因是2种算法选取的初始值不同时，迭代算法的传递函数差异较大，而不同的初始种群对GA的传递函数影响较小。反之，RSM-BP算法依赖于RSM的回归函数，初始值的改变对目标函数的影响显著。综上所述，从整体上看，基于GA-NN神经网络的预测模型是一种相比较更有效、快捷的优化工艺参数的方法。

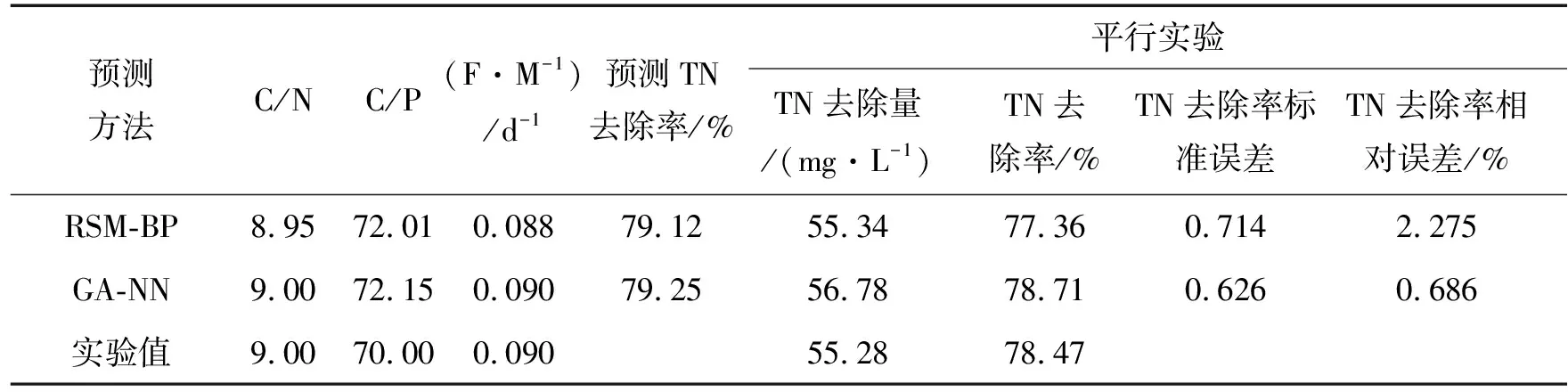
表5 不同方法预测TN去除率的对比验证Tab. 5 Comparison and verification of different methods to predict TN removal rate

3 讨论

关于污水处理厂脱氮工艺优化的文献较多[32-36]，但大多为正交试验优化。正交试验法仅从试验点角度寻找最优值，所得优化试验结果与真实最优值有较大差距。与正交试验法相比，基于响应面法的RSM试验，其原理是采用多元二次回归方程来拟合因子与响应值的函数关系，优化度高于正交试验，但最优值解极为依赖二次回归方程，且忽略了多项式阶数的影响。当受高阶多项式方程的影响较大时，会导致相对偏差值过大的现象，难以寻找出最优的区域面。ANN是通过构建数据正向传播和负向反馈的循环，将输出值和期望值之间的误差平方和最小化的方法，GA则是一种自适应算法。RSM-BP是将多元二次回归方程的优化值作为拟合因子，降低误差值，提高网络优化性能。GA-ANN是将均方误差函数作为适应度函数，且综合两者的评价准则，达到网络优化性能的目的。该优化方法不依赖于显式函数表达式，通过局部优化，减少了GA的搜索空间，提高了搜索效率，还具有良好的非线性仿真能力和非鲁棒性，利用数据可视化技术可以实现建模和优化过程的可视化。

本文基于RSM试验，二次回归方程的预测结果表明，模拟结果的R2为0.943 2，模拟结果较为准确；RSM-BP算法的R2为0.957 0,GA-NN算法的R2为0.985 3，表明GA-NN算法建模能力优于RSM和RSM-BP。通过对比RSM-BP算法与GA-NN算法的模拟结果发现，前者对TN去除率的预测结果低于后者，二者之差为-0.13%；在平行实验条件下，前者与后者对TN去除率和去除量的差值分别为1.35%和1.44 mg/L；2种算法的优化结果与优化条件下实验结果具有一定差异，前者的相对误差为2.275%，后者的相对误差为0.686%，前者是后者的3.32倍，说明RSM-BP算法的拟合效果不如GA-NN。同时，GA-NN算法得到的结果值与实验值更接近，二者之差仅为0.24%；RSM-BP算法得到的结果值与实验值相差较大，二者之差为1.11%，GA-NN算法在优化条件下的TN去除率较实验值稍高，准确度优于RSM-BP算法，但在TN去除量的准确度低于RSM-BP算法。这是因为：1)RSM-BP算法的优化条件中C/N和F/M与实验值差异较大，进水碳源的增加和污泥浓度的变化都有可能会造成误差，对实验结果也有一定的影响。2)GA-NN算法具有群体搜索特性，可对多个个体进行评估，评估函数不需要依赖于初始值，而RSM-BP算法需要依赖于RSM的回归函数，初始值的改变对目标函数的影响显著。但是，整体上GA-NN算法的迭代次数集中在0～50，而RSM-BP算法的迭代次数集中在0～18，前者的计算效率明显低于后者。即初始值离实验值偏差较大时，算法需要更多的迭代次数才能达到收敛状态。

综上所述，尽管本文GA-NN优化结果仅比RSM-BP优化结果值大1.35%，优化结果并不显著，但仍然表明了该方法具有可行性。这是因为GA-NN在优化过程中不需要增加额外试验，方法较为简单，这与丁海旭等[37]和黄辉等[38]试验方法类似，同时联级神经网络所得结果优于单一变量所得结果[39]，且TN去除率预测精度较高。

城市污水处理厂作为降解生活污水和工业废水的室外构筑物，其脱氮效果受到诸多因素的制约，尤其是温度因素。新疆冬季温度较低，会抑制微生物酶与底物的结合，导致酶促反应速率下降，生物活性降低。因此，本文将在后续研究中加入温度模型，以弥补该方法的不足，提高仿真模型的数据稳定性。

4 结论

采用单因素试验和RSM分析可知，各因素对TN去除率的影响由大到小顺序为：F/M、C/N、C/P，TN去除率最优工艺条件为：C/N=8.91，C/P=71.48，F/M=0.086 d-1，在此工艺条件下得到理论TN去除率为75.94%，去除量为53.59 mg/L。RSM-BP神经网络优化的最佳工艺参数为：C/N=8.95、C/P=72.01、F/M=0.088 d-1，最佳验证性能为13.62，TN去除率和去除量预测值分别为79.12%、55.34 mg/L；GA-NN算法优化的最佳工艺参数为：C/N=9.00、C/P=72.15、F/M=0.09 d-1，TN去除率和去除量的预测值分别为79.25%、56.78 mg/L。分别将RSM-BP与GA-NN的最佳工艺条件进行验证试验，得到TN去除率分别为77.36%、78.71%，说明GA-NN神经网络更加适合于A2/O工艺脱氮的优化和预测，同时可为污水处理厂出水TN浓度达标排放提供参考。