脉冲推力作用下上楼梯双足机器人行走的建模与动力学分析

陈嘉睿，凌 琳，蒋贵荣

(桂林电子科技大学 数学与计算科学学院, 广西 桂林 541004)

1990年，McGeer[1]首次提出“被动动态行走”概念。与传统双足机器人不同，被动行走机器人能够在没有任何输入情况下，以循环步态在平缓的下坡上行走。考虑机器人行走的基本特征，学者们建立机器人行走的模型，进而研究其复杂的动力学行为[2-4]。

与平路双足机器人相比，上楼梯双足机器人的研究更复杂且更具挑战性，这是由于楼梯具有复杂几何形状，且双足机器人在爬升楼梯过程中抬腿高度增加、能量损失增多，使得双足机器人的行走稳定性降低。为解决这些难题，人们设计了带膝关节或带伸缩腿的上楼梯双足机器人，并给出步态规划[13-14]。Shih等[15]设计一个具有最简单双足结构的7-DOF 双足机器人，该机器人有2条可变长度的腿，用于模拟人类行走时的膝关节；文献[16]采用运动力控制方案结合遗传算法(GA)，讨论机器人斜坡上行走的最佳步行速度；文献[17]开发了机器人步态的基于转矩的比例积分-微分(PID)控制器。

综上，上楼梯双足机器人行走的步态规划和控制算法方面取得了很多成果，但行走动力学的理论研究有待深入。Kuo[11]和HAO等[18]认为摆动阶段中在关节处施加力矩，可以保证系统极限环的存在，从而提高机器人行走的稳定性。由于存在摆动腿与楼梯的碰撞切换，上楼梯双足机器人行走也是一种碰撞模型[19]，具有复杂的动力学行为。

本文考虑伸缩腿结构以解决上楼梯的触碰台阶等问题，采用幅值限制和与支撑腿角速度相关的脉冲推力作为上楼梯双足机器人的动力源。摆动阶段在关节处施加力矩，提高机器人行走的稳定性。通过理论分析和数值模拟，研究上楼梯双足机器人行走的复杂动力学行为，比较可调节脉冲推力和固定脉冲推力的性能，验证可调节脉冲推力的有效性，讨论脉冲参数与系统自身结构参数对系统稳定性的影响。

1 上楼梯双足机器人行走模型

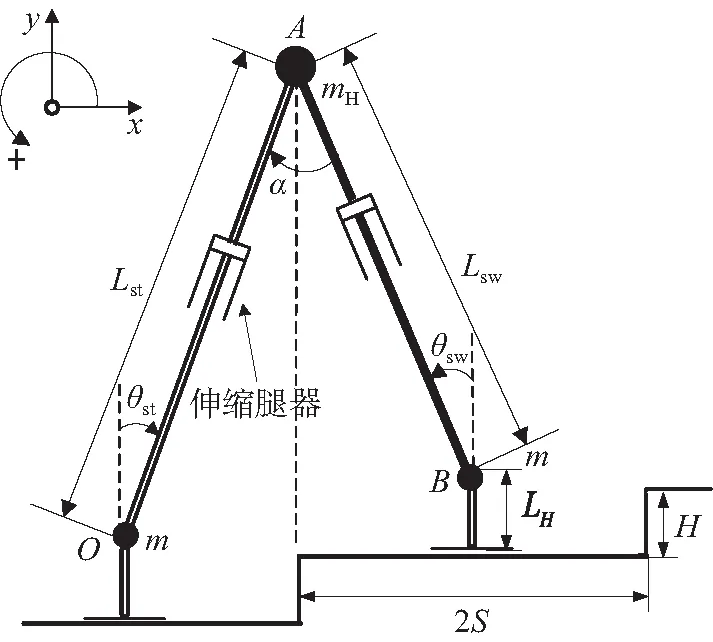
图1 上楼梯双足机器人模型示意Fig. 1 Schematic representation of the model of ascending stair biped robot

双足机器人左右对称、前后对称，以支撑腿的质点为原点O建立二维角坐标系，A为髋关节质点，B为摆动腿踝关节质点。机器人初始姿态为两只脚分别落在阶梯中间 (支撑腿位于摆动腿的前方)，髋关节质点A投影在楼梯边缘上。在运动过程中，双足机器人的支撑腿的脚部始终贴紧平面且不发生滑动，脚踝以下部分不发生转动。

如图2所示，双足机器人上楼梯过程有4个阶段：支撑腿伸长前摆、支撑腿伸长瞬间、支撑腿伸长后摆以及碰撞切换瞬间。本文提出的上楼梯过程描述如下：(I-II) 此阶段双足机器人双腿等长，即Lst=Lsw=l0(l0为常数)，做类似于最简双足机器人摆动阶段的运动，支撑腿绕踝关节向前摆动直至与台阶平面垂直；(II-III)为支撑腿伸长阶段，此阶段发生于θst=0, 支撑腿的长度由l0伸长至L0,且该伸长过程是瞬时完成；(III-IV) 支撑腿继续绕踝关节向前摆动，直至摆动腿运动到下一级阶梯平面；(IV)为碰撞阶段, 在原支撑腿踝关节处施加沿其指向髋关节方向的脉冲推力p,在p的作用下支撑腿离地，完成双腿角色转换。另外，为了避免新摆动腿与楼梯发生擦碰，碰撞发生的同时，新摆动腿由L0伸长至l0，且踝关节以下部分被收回。阶段IV完成后，新摆动腿与新支撑腿处于下一步行走的初始状态。

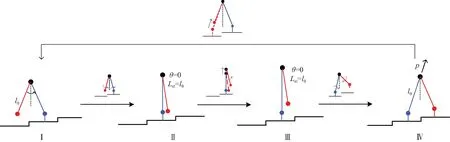
图2 上楼梯双足机器人步态示意Fig. 2 Gait diagram of ascending stair biped robot。

双足机器人在上楼梯过程中单腿支撑的摆动阶段分为支撑腿伸长前摆动阶段(I-II)和支撑腿伸长后摆动阶段(III-IV)，这2个阶段都可以根据拉格朗日方程推出机械系统的摆动阶段动力方程，机器人的动态方程由连续微分方程表示。在支撑腿伸长阶段和碰撞阶段，机器人的状态变化可以根据动量矩守恒通过代数映射函数来表示。

1.1 支撑腿伸长前的摆动阶段

在阶段I-II，机器人双腿的长度均为l0, 支撑腿与地面无弹起和相对滑动，摆动腿向前摆动。本阶段采用拉格朗日方程得到双足机器人摆动运动时的动力学模型。以支撑腿踝关节质点为原点，建立直角坐标系，定义拉格朗日方程为

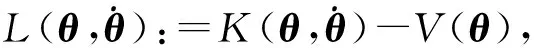
式中K和V分别为系统的动能和势能。根据哈密顿原理，运动方程可以从以下拉格朗日方程得到

(1)

式中Fi为施加到质点上的广义力。分别计算系统的动能和势能，可得拉格朗日表达式为

(2)

将式(2)代入式(1)，整理可得

(3)

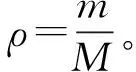
1.2 支撑腿伸长阶段

在阶段III中，支撑腿运动到与台阶垂直位置的瞬间，支撑腿的伸缩装置开始作用，该阶段的条件可表示为

HS1={θ∈R2:T(θ)=θst=0}。

除重力外，双足机器人整体只在支撑腿踝关节受到外力作用，机器人整体关于O点的角动量守恒，如式(4)。摆动腿仅受到髋关节A处的外力作用，摆动腿关于髋关节A的角动量守恒，如式(5)。

(4)

(5)

支撑腿伸长前后，双足机器人关于支撑腿的角动量以及摆动腿关于髋关节的角动量都是守恒的，即满足

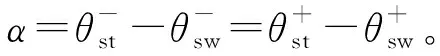
1.3 支撑腿伸长后的摆动阶段

在阶段IV，机器人支撑腿长度为L0,摆动腿长度为l0，摆动腿向前摆动。本阶段采用拉格朗日方程得到双足机器人摆动运动时的动力学模型。

分别计算系统的动能和势能，可得拉格朗日表达式为

(6)

将式(6)代入式(1)，整理可得

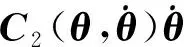
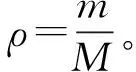
1.4 摆动腿与楼梯碰撞切换阶段

在上述假设条件下，当满足以下3个条件时，即为冲击阶段。

① 摆动腿到达下一级楼梯表面；

② 摆动腿向下移动；

③ 摆动腿运动到支撑腿前方,且两脚质点水平相距2S。

这3种冲击条件可以分别由以下集合HS2转换

(7)

由假设可知，双足机器人发生碰撞时，摆动腿与楼梯表面的接触是刚性的，即非弹性的。双足机器人在行走周期结束时发生刚性碰撞，碰撞是瞬间发生的，阶梯对于摆动腿的作用力被建模为脉冲矢量，摆动腿与行走下一级阶梯瞬时碰撞会导致两条腿和站姿发生转换，摆动腿变成站姿腿，反之亦然。在此过程中，双足机器人的配置变量不变，但广义速度会发生跳跃。瞬间碰撞切换模型如图3所示(V-和V+分别为施加脉冲推力前髋关节的运动速度和地面冲击后髋关节的运动速度)。

图3 双足机器人的瞬时碰撞模型Fig. 3 Instantaneous collision switching model for bipedal robots

由图3的几何条件，很容易求出碰撞前后的各自由度变换关系以及双腿长度间的关系如下

(8)

(9)

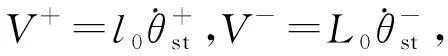
(10)

由摆动腿关于髋关节的动量矩守恒可得如下关系：

(11)

结合式(11)，双足机器人碰撞前后的状态变化关系可以用代数方程描述，写成矩阵的形式如下

1.5 上楼梯双足机器人步态的脉冲混杂模型

带伸缩装置的上楼梯双足机器人的周期步态包括4个阶段：支撑腿未伸长的摆动阶段、支撑腿伸长阶段、支撑腿伸长后的摆动阶段以及摆动腿与阶梯碰撞切换阶段。利用拉格朗日动力学原理和角动量守恒原理建立上楼梯双足机器人的动力学方程，其中支撑腿伸长前后的摆动阶段都可以由连续型非线性微分方程描述；支撑腿伸长过程和摆动腿与阶梯碰撞过程都可以由离散型代数切换映射描述，因此上楼梯双足机器人的动力学模型可表示为由多个连续型非线性微分方程和多个离散型代数映射构成的脉冲混杂系统。

(12)

式中：Ω1⊆R4,Ω2⊆R4;HS1,HS2分别定义如下：

HS1={x∈R2:T(x)=θst=0},

HS2={x∈R4:Υ1(x)=H,Υ2(x)<0,Υ3(x)=2S},

fi(x)、Δi(x)以及g(x)分别为

2 庞加莱映射

2.1 脉冲推力

(13)

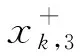
即pk满足

2.2 庞加莱映射

庞加莱映射是一种研究周期运动稳定性及其随参数变化的分岔特征的几何方法。为了建立上楼梯双足机器人动态行走步态对应的庞加莱映射，选取摆动腿与阶梯碰撞后瞬间机器人的状态所在的超平面作为庞加莱截面，记为Σ; 定义庞加莱映射为Φ:Σ→Σ，其中

在庞加莱截面上取一点x0∈Σ作为系统的初始状态，记xk为系统第k次返回截面∑的状态变量，则庞加莱映射Φ:Σ→Σ可表示为

xk+1=Φ(xk)。

若存在一点xd∈Σ，满足

xd=Φ(xd),

则称xd为庞加莱映射的不动点，生成的庞加莱映射的不动点可用于分析行走模式和构建模型分岔图。

2.3 稳定性分析

运用庞加莱映射方法，通过分析系统不动点的稳定性来分析行走稳定性。

假设系统不动点为xd，对其施加微小扰动Δxd，扰动点经庞加莱映射作用后为x*, 采用泰勒级数展开， 则有

x*=Φ(xd+Δxd)=Φ(xd)+JΔxd,

式中J为庞加莱映射函数相对于系统状态的梯度，称为雅可比矩阵，其表达式为

行走中的误差通过雅可比矩阵J传递，J决定了不动点的稳定性[9]，若J的最大特征值λm的模小于1或所有特征值均在复平面单位圆里，则误差会逐渐消除，行走是稳定的；反之，行走的误差会随着步数增加而被放大，行走不稳定。特别地，当J存在一个特征值λ0=-1时，则有一个超临界的Flip分岔，此时一个周期-2解从周期-1分岔出来。

3 仿真实验及分析

3.1 周期步态的初始条件及参数设置

假设一周期步行时间为T，双足机器人上楼梯的过程被分为4个阶段：支撑腿伸长前摆动阶段(0～Ts)、支撑腿伸长阶段(Ts)、支撑腿伸长后摆动阶段(Ts～T)以及碰撞阶段(T)。

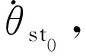
(14)

周期步态参数设置的具体流程如图4所示。

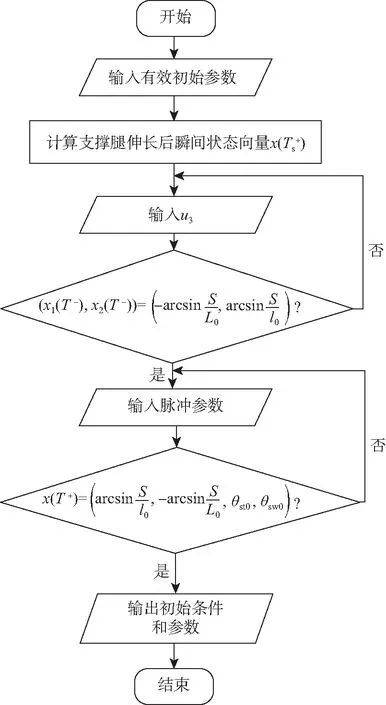
图4 周期步态参数设置的流程Fig. 4 Flowchart for setting parameters of the cycle gait

3.2 上楼梯双足机器人模型的稳定周期步态

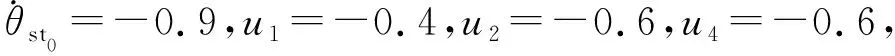
如图5(a)所示，将不动点xd作为初始状态，上楼梯双足机器人的状态在相空间中形成一个稳定的极限环，其中点R1(K1)对应支撑腿(摆动腿)运动的初始点；点R2(K2)对应支撑腿(摆动腿)在图2中(I-II)和(II-III)状态之间的切换点；点R3(K3)对应支撑腿(摆动腿)在图2中(II-III)和(III-IV)状态之间的切换点；点R4(K4)对应支撑腿(摆动腿)在摆动足发生瞬间的碰撞切换点。点Ri和点Ki(i=1, 2, 3, 4)分别表示支撑腿和摆动腿在一个周期步态内4个阶段的切换点。图5(b)为双足机器人稳定的周期-1步态下双腿的角度和角位移的时间序列，可以看出在周期-1步态中支撑腿的角位移由正值逐渐减小到零后变为负值再逐渐增大，摆动腿角位移则是由负值向正方向运动直至最大角位移处，随后摆动腿做“回摆”运动，此时摆动角位移逐渐减小。图6所表示的是扰动解的相图与时间序列，由图6(a)可知，系统从出发的轨线趋向于对应不动点的周期-1解。图6(b)表示以扰动点为初始点的双足机器人双腿的角度和角位移随时间变化逐渐稳定。图7为双足机器人上楼梯的棍棒示意。结合图5～7可以看出该双足机器人在这组参数下具有稳定的周期步态。

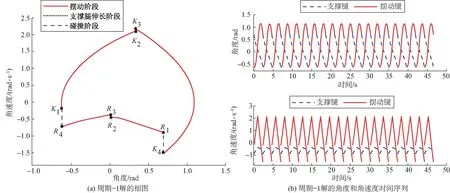
图5 系统(12)在b=3.12,d=3.12,c=2.9 时的周期-1解Fig. 5 Period -1 gait for system (12) with b=3.12,d=3.12,c=2.9

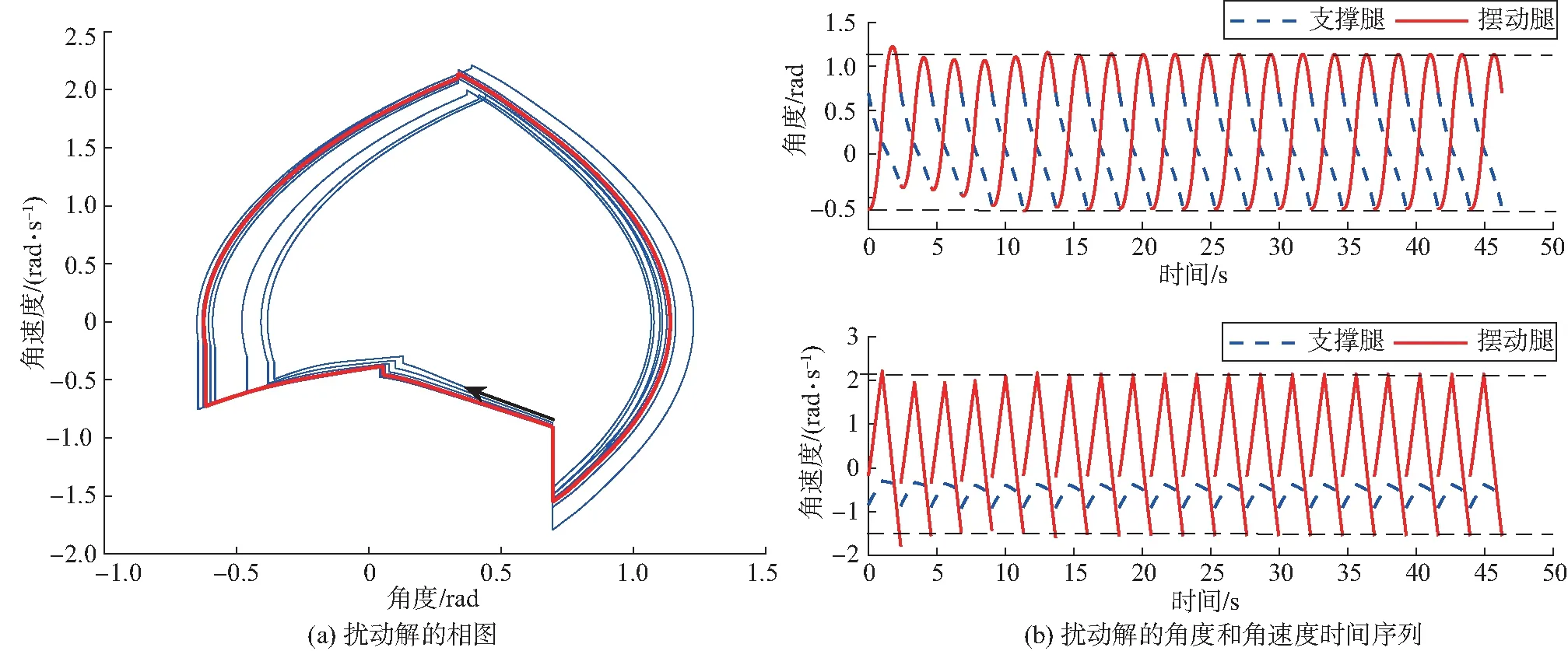
图6 系统(12)在b=3.12,d=3.12,c=2.9，初始点为[0.694 5,-0.627 6,-0.840 0,-0.170 0]T时的扰动解Fig. 6 For system(12) with b=3.12,d=3.12,c=2.9, a gait of perturbation solutions starting from the point [0.694 5,-0.627 6,-0.840 ,-0.170 0]T

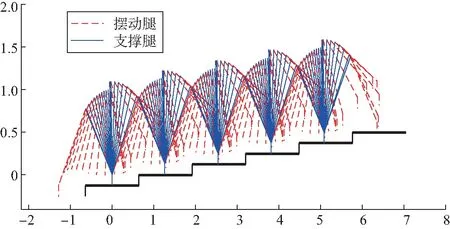
图7 以[0.694 5,-0.627 6,-0.904 0,-0.185 0]T为初始点,b=3.12,d=3.12,c=2.9 的双足机器人上楼梯的棍棒图Fig. 7 Stick diagram of ascending stair biped robot with b=3.12,d=3.12,c=2.9,and the initial point [0.694 5,-0.627 6,-0.904 0,-0.185 0]T

3.3 可调节脉冲力和固定脉冲力的性能比较

依然选取xd=[0.694 5,-0.627 6,-0.904 0,-0.185 0]T为初始状态向量，其他初始参数不变，比较输入不同种类的脉冲力对系统的影响。

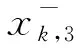
图8 系统(12) 分别在可调节脉冲(b=3.12,d=3.12,c=2.9)和固定脉冲pd=7.251作用下的效果Fig. 8 Effects of system (12) under the action of adjustable impluse (b=3.12,d=3.12,c=2.9) and fixed impluse pd=7.251, respectively

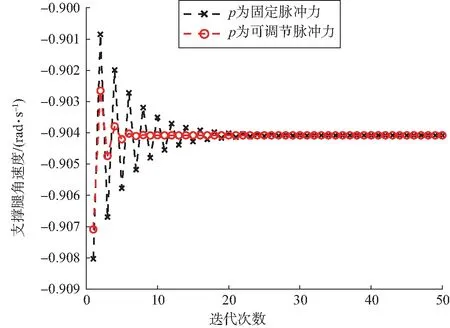
图9 系统(12)分别在可调节脉冲(b=3.12,d=3.12,c=2.9)和固定脉冲pd=7.251作用下碰撞后支撑腿的角速度变化Fig. 9 Variation diagram of angular velocity of the standing leg just after the collision for system (12) under the action of adjustable impluse (b=3.12,d=3.12,c=2.9) and fixed impluse pd=7.251, respectively

3.4 周期步态的分岔

在环境参数或自身结构参数发生改变的情况下，当参数变化到一个临界值时，系统变为不稳定，双足机器人动态行走呈现倍周期步态或混沌步态。

3.4.1 特征值分布

基于2.3节中的理论，采用数值方法求解J的特征值，并分析其在复平面空间的分布情况。

图10和图11分别为稳定周期-1解和Flip分岔的特征值在复平面的空间分布图。如图10 所示，对3.2节中的不动点xd=[0.694 5,-0.627 6,-0.904 0,-0.185 0]T施加微小扰动，其雅可比矩阵J的所有特征值均在复平面单位圆内，即最大特征值的模小于1，所以不动点是稳定的，机器人具有稳定周期-1步态。图11反映了Flip分岔现象的特征值分布，采用相同初始状态施加微小扰动，其他参数固定不变，输入脉冲参数为d=-3,c=5,b=- 0.99时系统达到临界值。由图11(b)可知，当b=-0.99 时，雅可比矩阵存在一个λ*≈-1，当b=-1时，有λ*<-1,此时，一个周期-2解从周期-1分岔出来。

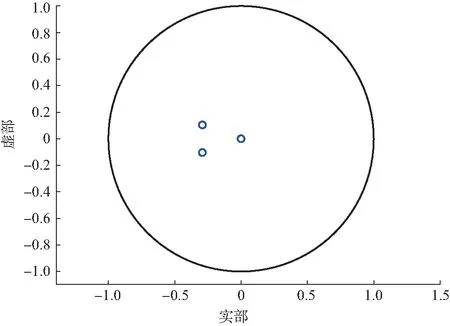
图10 系统(12)在b=3.12,d=3.12,c=2.9时周期轨道的所有特征值分布Fig. 10 Distribution diagram of all eigenvalues of the periodic orbit for system (12) with b=3.12,d=3.12,c=2.9

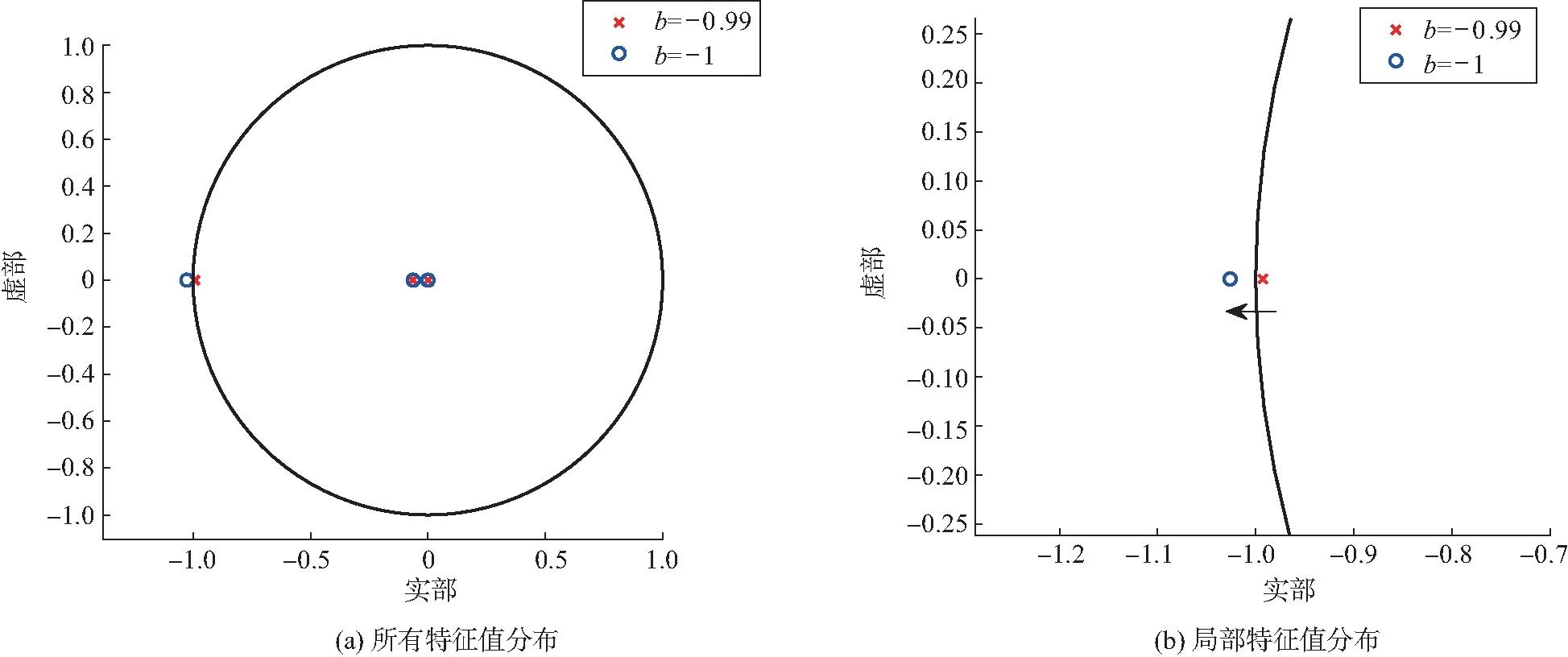
图11 系统(12)在d=-3,c=5，b分别取-0.99和-1时的特征值分布Fig. 11 Eigenvalue distribution for system (12) with d=3.12,c=2.9, and b is taken as -0.99 and -1, respectively

3.4.2 脉冲参数分析

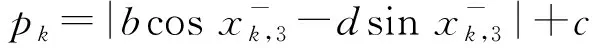
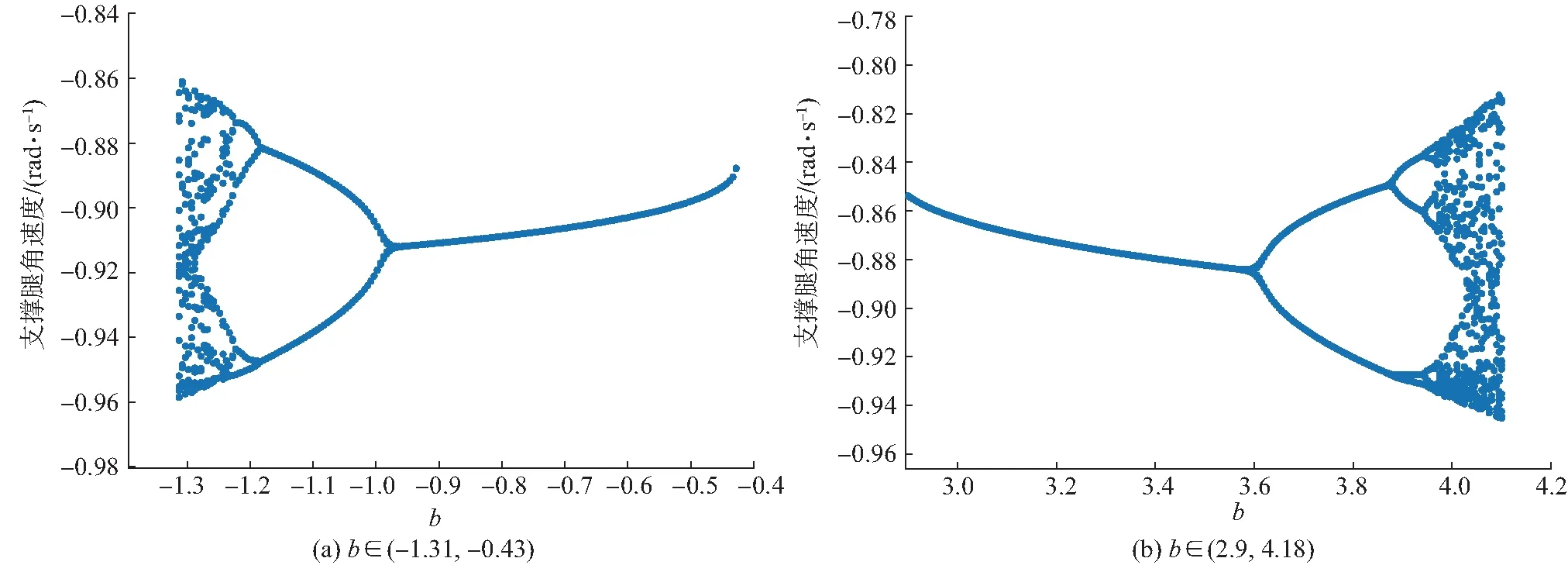
图12 系统(12)在d=-3,c=5时的周期解的分岔Fig. 12 Bifurcation diagram of system (12) with d=-3,c=5

图13 系统(12)在b=-1,c=5时周期解的分岔Fig. 13 Bifurcation diagram of system (12) with b=-1,c=5

3.4.3 髋关节质点参数分析

影响双足机器人稳定步态的因素还有自身结构参数，接下来分析髋关节质点对系统稳定性的影响。将髋关节质量mH视为变量，固定其他参数(b=5，d=-7,c=5,m=0.5), 如图14所示，随着mH由10.8减小至约为10.02时，系统出现分岔。

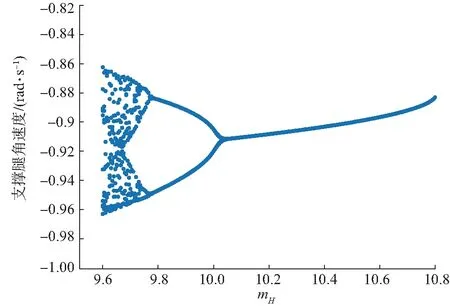
图14 系统(12)在b=5，d=-7,c=5,m=0.5时的周期解分岔，mH∈(9.6,10.8)Fig. 14 Bifurcation diagram of system (12) with b=5，d=-7,c=5,m=0.5, mH∈(9.6,10.8)

4 结语

本文研究脉冲推力作用下带伸缩腿上楼梯双足机器人行走的复杂动力学。引入一种与支撑腿角速度相关且存在幅值限制的脉冲推力，运用拉格朗日方程和角动量守恒定律建立上楼梯双足机器人的动力学模型。利用庞加莱映射分析带伸缩腿上楼梯双足机器人行走的稳定性,讨论脉冲参数b和d以及自身结构参数mH对周期-1步态存在、稳定以及分岔的影响。

理论分析和仿真实验结论表明：当选择合适的参数时，系统存在稳定的周期-1步态，即双足机器人能稳定地上楼梯；与支撑腿角速度相关且存在幅值限制的脉冲推力优于固定的常值脉冲推力，能让上楼梯双足机器人快速进入稳定的行走状态。这些结论为上楼梯双足机器人实际行走的稳定与控制提供了理论依据。