智能反射面辅助的毫米波MIMO系统波束成形设计*
2023-01-18戈忠义岳殿武李光辉魏思悦苏雨苗
戈忠义,岳殿武,李光辉,魏思悦,苏雨苗
(大连海事大学 信息科学技术学院,辽宁 大连 116026)
0 引 言
随着无线通信技术的快速发展,移动网络对于传输速率的需求不断提高,发展高频大规模天线阵列技术迫在眉睫。由于在毫米波(Millimeter-Wave,mmWave)频率下波长较短,可以在更小空间内封装更多的天线[1],且大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)技术与毫米波系统搭配在一起可形成特定方向的光束,利用高空间复用增益虽可以实现更高的传输速率,但这种定向性也使得毫米波通信更容易受到遮挡物的影响而不能正常通信,这种问题在高密度城市集群中更加明显[2]。
最近出现的智能反射面技术能够通过重新配置无线传播环境以达到更好的通信质量[3],有望用来解决上述阻塞问题。智能反射面是由大量成本低廉的被动反射元件构成,每个元件都能独立调整信号相移[4]。业内人士普遍认为智能反射面将会在5G末期甚至未来6G通信网络中扮演极其重要的角色[5-6]。
在智能反射面辅助下行通信系统中,为了优化系统性能,常见的一个问题是需要协同优化基站端预编码矩阵和反射面的反射系数。例如,在利用反射面提高数据传输速率时,反射面相位必须与基站端的主动波束形成权重,然后再进行优化[7]。另外,为了提高信号接收强度和数据吞吐量,用户端搭载多个天线以同时接收多条数据流。在现有的研究中,文献[8]提出了一种交叉熵算法,通过随机相位求原始速率,在其中选出较好的速率值,然后基于较好的速率值更新下次选择更优相位的概率,迭代多次后选出对应最好速率的相移矩阵,然而这种优化处理方案会造成严重的性能损失。文献[9]采用交替优化算法进行和速率性能的优化,这种方法通过固定其他优化参数,按顺序迭代优化一个参数,虽然实现了不错的性能,但在实际系统中其过高的复杂度是难以被接受的。
最近,针对智能反射面辅助的毫米波MIMO系统的优化设计,文献[10]采用了一种基于最小均方误差算法的方案,但这种方案得到的奇异值(幅度)通常小于基于流形优化方案所获得的奇异值(幅度),而且基于流形优化方案可以获得更加平衡、分布更均匀的奇异值[7]。在文献[11]中,作者虽采用了复杂度较低的流形优化算法方案进行了优化处理,但只考虑了单用户场景。鉴于此,本文考虑了多用户场景下毫米波MIMO下行系统的流形优化问题,目标是通过协同优化智能反射面的反射系数、预编码矩阵、合并矩阵以及功率分配来最大化多用户的和速率,研究重点是利用毫米波信道的内在结构解决智能反射面的相移优化问题。仿真结果表明,通过流形优化技术处理可以显著提升多用户和速率,且与文献[10]中的最小均方误差方案相比,性能提升更明显。
1 系统模型
本文考虑了一个毫米波MIMO下行系统。假定直连链路被阻塞,在基站和用户之间部署一个智能反射面协助通信,如图1所示。
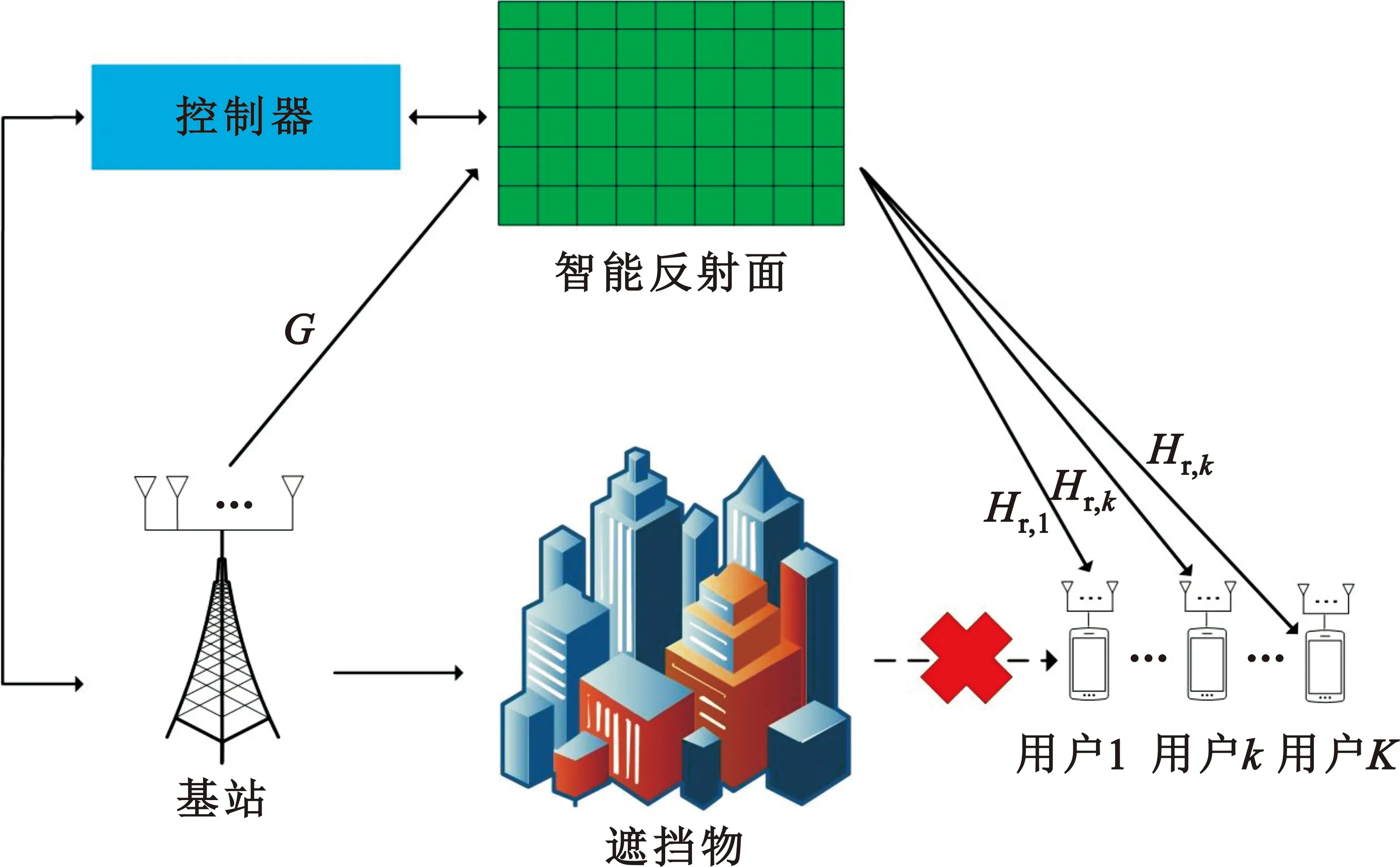
图1 智能反射面辅助的毫米波MIMO系统
基站配备Nt个天线同时服务K个用户,且每个用户搭载Nr个天线。为了提高数据吞吐量,基站至反射面再到用户一侧发送Ns条数据流,且反射面由N个无源反射元件组成。由于文献[3]中已经讨论了多种信道估计方法,因此假设基站和反射面都可以获得完美的信道状态信息。G∈N×Nt,Hr,k∈Nr×N分别表示基站至反射面和反射面至第k个用户的毫米波信道。采用传统的Saleh-Valenzuela(SV)模型捕获毫米波信道的特征[12],且假设基站和用户端的天线阵列采用均匀线性阵列(Uniform Linear Array,ULA),反射面的天线阵列采用均匀平面阵列(Uniform Plannar Array,UPA)。这样信道矩阵G和Hr,k可表示为如下形式:
(1)
(2)
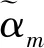
(3)
式中:λ代表信号波长,d代表天线间距,且为了实现天线间的独立性,一般情况下设置d=λ/2。对于采用均匀平面阵列分布且元件数为N的归一化阵列响应向量如下:
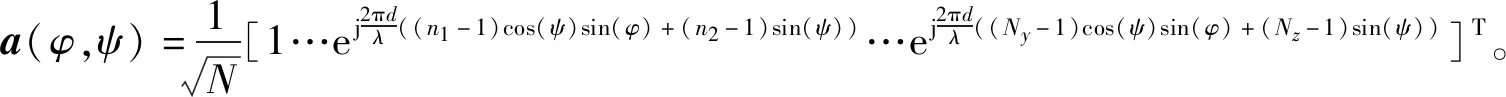
(4)
式中:N=Ny×Nz。另外,本文也考虑到了视线路径以及非视线路径的路径损耗,具体表达式和数值设定将在第3节中给出。
在基站端,基带预编码矩阵表示为F=[f1,f2,…,fK]∈Nt×KNs且是发送功率。发送信号s=[s1,s2…,sK]T∈KNs×1且满足定义第k个用户的等效信道如下:
Hk=Hr,kΘG。
(5)
第k个用户接收到的信号可表示如下:
(6)
式中:wk∈Nr×Ns是第k个用户的合并向量且满足表示反射面的无源波束成形矩阵且θn代表第n个反射元素的相移;表示用户k处的加性高斯白噪声,即服从均值为0、方差为的复高斯分布。下行链路的第k个用户的信干噪比(Signal-to-Interference plus Noise Ratio,SINR)可表示如下:
(7)
式中:fkns(wkns)表示第k个用户第ns条数据流的预编码向量(合并向量)且kns=(k-1)Ns+ns[13]。因此,可达到的和速率表达如下:
(8)
2 优化算法设计
2.1 描述问题
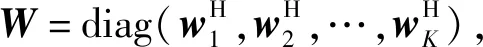
(9a)
(9b)
(9c)
Θ=diag(ejθ1,ejθ2,…,ejθN)。
(9d)
为了简化上述问题,可以在解决一个矩阵问题的同时固定其他矩阵,然后在每次迭代中交替更新所有矩阵。对于给定Θ时,采用奇异值分解(Singular Value Decomposition,SVD)方法求解预编码矩阵F和合并矩阵W,且利用注水功率分配法求解最优功率分配。对于有效信道Hk的奇异值分解如下:
Hk=UΣVH=[U1…Uk…UK]·
(10)
式中:U是一个Nr×Y的酉矩阵;Σ是一个Y×Y的奇异值对角矩阵;V是一个Nt×Y的酉矩阵,其中Y=rank(Hk);矩阵Σk是一个Ns×Ns的矩阵,本文中我们设置Ns≪min{Nt,Nr,Y};Vk是一个Nt×Ns的矩阵。若给出固定的Θ,那么问题(9)的最优解决方案如下:
(11)
Wopt=Uk。
(12)
式中:
Γ=diag(P1,P2,…,PNs),
(13)
将Fopt和Wopt代入公式(9),就可以得到一个只考虑优化无源波束成形矩阵Θ的问题:
(14a)
s.t.Θ=diag(ejθ1,ejθ2,…,ejθN)。
(14b)
2.2 基于流形优化算法的方案
展开Hk=Hr,kΘG,并重新表示如下:
Hk=Hr,kΘG=
(15)
式中:ATBS、ARUE和E(n,m,k)表示如下:
(16)
(17)
(18)
并且公式(18)中的enmk再展开如下:
vHgnmk。
(19)
式中:v=diag(ΘH);gnmk中的∘代表哈达玛(Hadamard)积;enmk表示与第(k,m,n)条从基站至反射面再到用户端复合路径有关的无源被动波束成形增益。
对于搭配M个天线的均匀线性阵列分布,可知
|aH(ηm)a(ηn)|→0,M→∞,且任意sin(ηm)≠sin(ηn)。
(20)
(21a)
s.t.E(ns,ns,k)=αnsβns,kensnsk,
(21b)
∀ns∈{1,2,…,Ns},∀k∈{1,2,…,K},
(21c)
ensnsk=vHgnsnsk,
(21d)
v=[ejθ1,ejθ2,…,ejθN]H。
(21e)
这样,可以通过求解(21)等效地求解问题(14)。
接下来,将式(18)代入式(21)中,表达如下:
(22a)
s.t.v=[ejθ1,ejθ2,…,ejθN]H。
(22b)
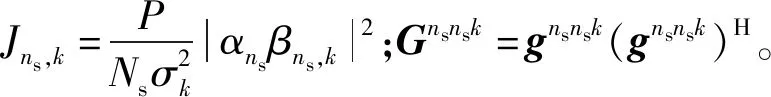
问题(22)搜索空间可认为是N个复圆乘积,如下:

(23)
式中:xi是向量x的第i个元素且每个复圆S={x∈:x*x=Re{x}2+Im{x}2=1}是的一个子圆。本文的流形优化方案主要思想是基于(23)定义的流形空间的梯度下降算法[7],算法中的切空间是由在点vt至的所有切向量组成的集合[15],表达式如下:

(24)
在所有的切向量中,类似于欧氏空间,其中与负黎曼梯度相关的方向代表目标函数下降最快的方向[17]。要优化的目标函数如下:
(25)
对于复圆流形,f(v)在vt点的黎曼梯度是一个切向量grad(f(vt))[15],表达式如下:

(26)

(27)
求解上述欧几里得梯度会涉及到关于复值矩阵求解导数的方法,具体细节可以参见文献[18]。然后,根据每一个步长τt更新vt,表达式如下:
(28)
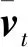
(29)
2.3 计算复杂度分析
基于流形优化算法方案的复杂度主要来自于求解欧几里得梯度(28),复杂度的量级为O(N),则求解v的复杂度为O(NIite),其中Iite为迭代次数。另外,计算Hk的奇异值分解时复杂度为O(N),所以流形优化算法方案的整体复杂度为O(N2Iite)。然而最小均方误差(Minimum Mean Square Error,MMSE)算法的复杂度为O(N3+IinN2)Iout,其中Iin和Iopt分别表示内部和外部循环迭代次数[7]。不难看出,基于流形优化算法的复杂度明显低于基于MMSE算法的复杂度。
基于智能反射面的流形优化算法步骤如下:
1 初始化v0并且设置一个预定义的阈值ε。
2 开始循环:
4 使用式(26)计算黎曼梯度grad(f(vt));
5 设置一个合适的Armijo步长τt;
7 使用式(29)更新vt+1;
8 直到两次迭代之间的目标函数值之小于预先设定的阈值ε,结束循环。
9 输出最优的v*。
3 仿真结果分析
在多用户(K=4)情况下,本文通过仿真结果对比流形优化方案、文献[10]中的最小均方误差方案以及随机相位方案的性能。在仿真中,采用三维坐标表示基站、反射面以及用户的位置,单位为m。基站和反射面的坐标分别设置为(3,0,10)m和(0,100,10)m,4个用户的坐标分别设置为(3,150,1.8)m、(4,150,1.8)m、(5,150,1.8)m以及(6,150,1.8)m。由于要考虑发射和接收天线增益,所以多用户的信道重新表达如下[11]:
Hk=GtGrHr,kΘG。
(30)
式中:Gt和Gr分别表示发射和接收天线增益,且设置Gt=Gr=21 dB。基站至反射面的信道G和反射面至多用户的信道Hr,k表示如下:
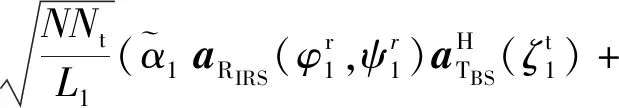
(31)
(32)
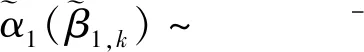
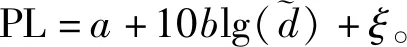
(33)
图2展示了多用户和速率与发射天线个数之间的关系,其中设置接收天线个数Nr=15、反射面元素个数N=100以及发射功率P=30 dBm。从图2中可以看出,在三种方案对应的多用户和速率性能方面,随着发射天线个数的不断增加,基于流形优化方案明显好于基于最小均方误差方案和随机相位方案,而且可以发现基于流形优化方案实现的和速率大小是基于随机相位方案的1.5倍左右。
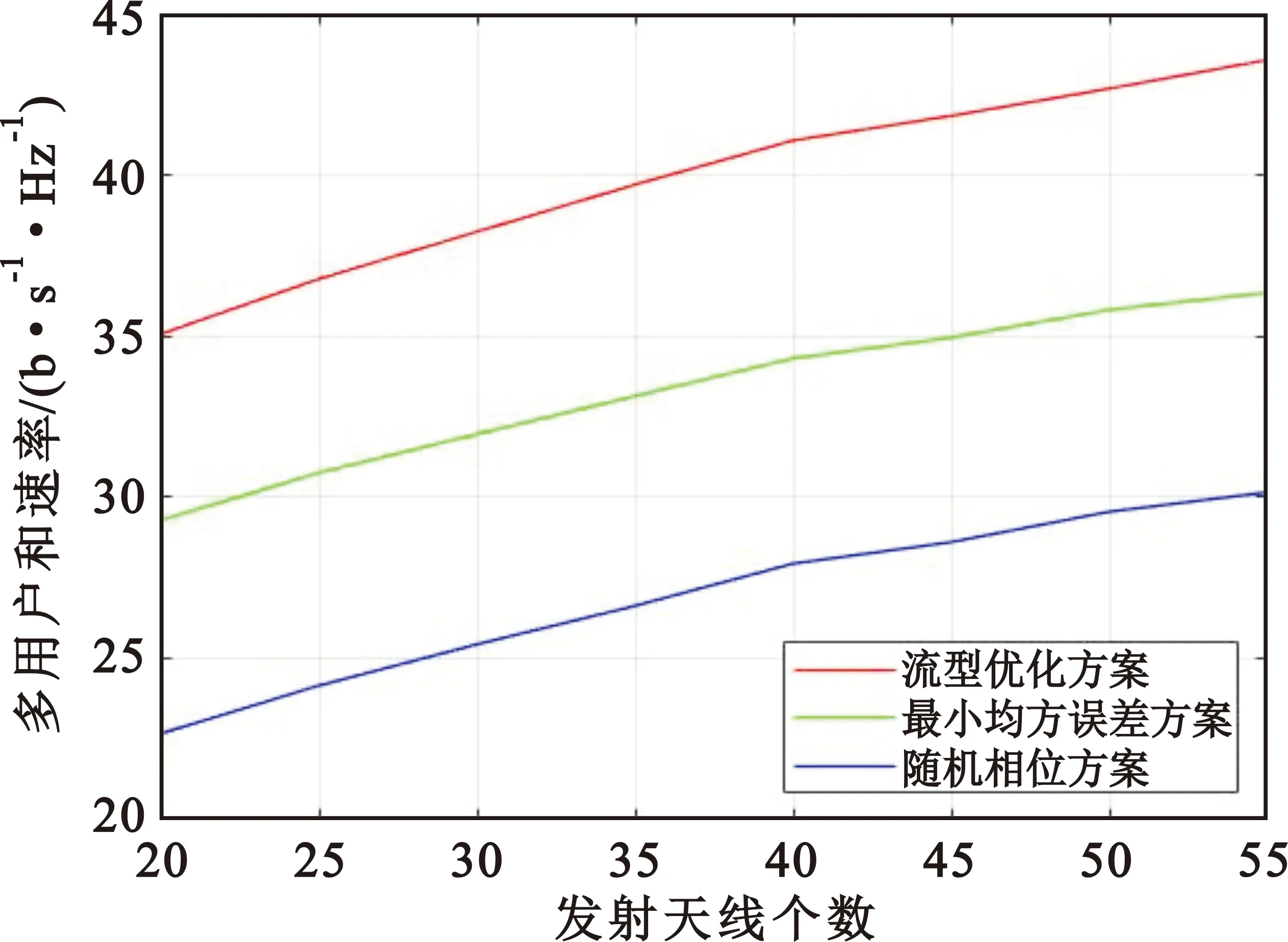
图2 智能反射面辅助的毫米波MIMO系统多用户和速率与发射天线个数之间的关系
图3展示了多用户和速率与发射功率之间的关系,其中设置发射和接收天线个数分别为Nt=20、Nr=15以及反射面元素个数N=100。从图3中不难看出,在多用户和速率性能方面,随着发射功率的不断增加,三种方案对应的多用户和速率性能都在持续提高,但基于流形优化方案一直都好于基于最小均方误差方案和随机相位方案。另外,随机相位方案发射功率达到30 dBm时,与流形优化方案发射功率为21 dBm接近,这也从侧面说明了优化算法对于智能反射面的重要作用。
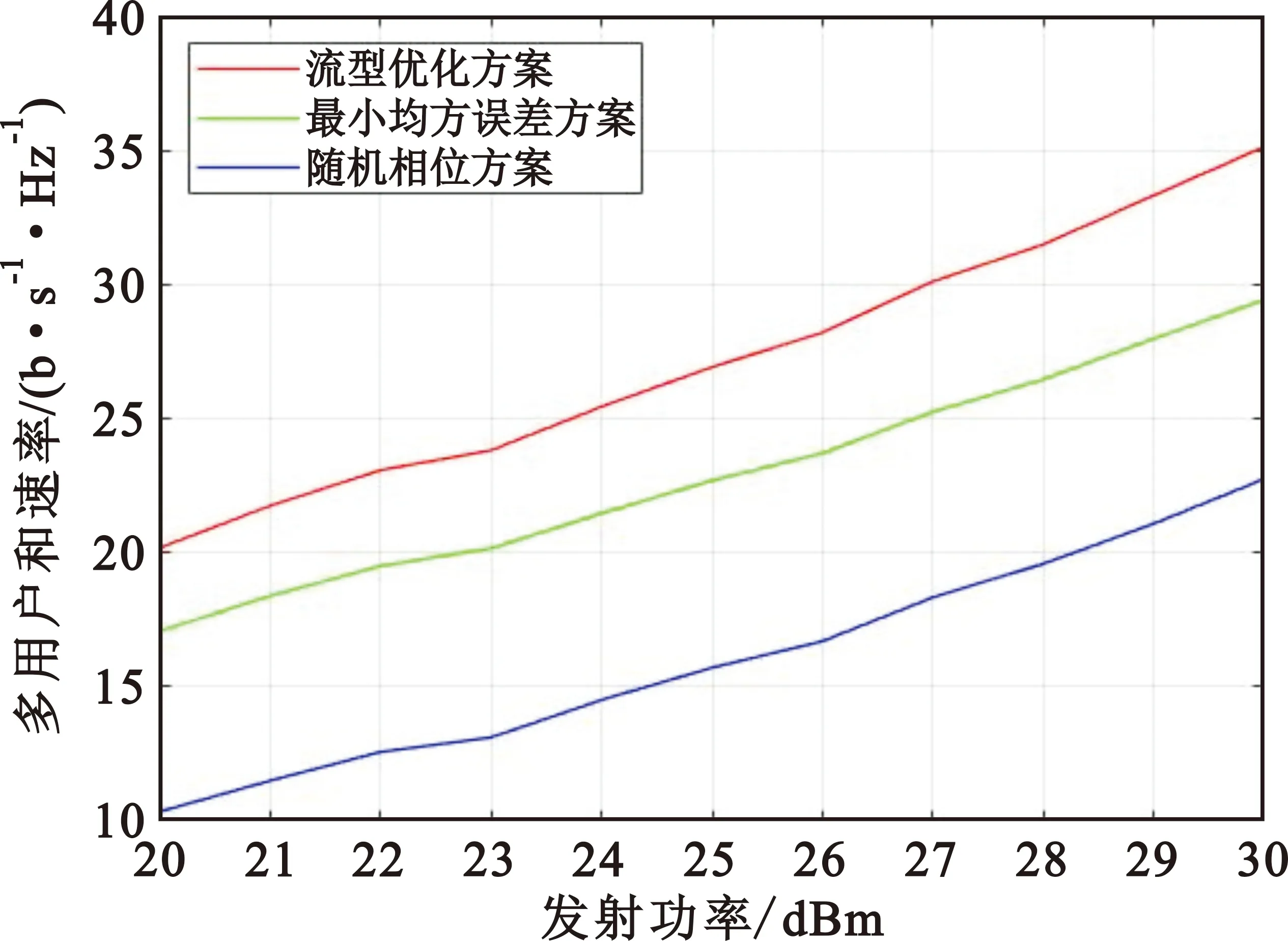
图3 智能反射面辅助的毫米波MIMO系统多用户和速率与发射功率之间的关系

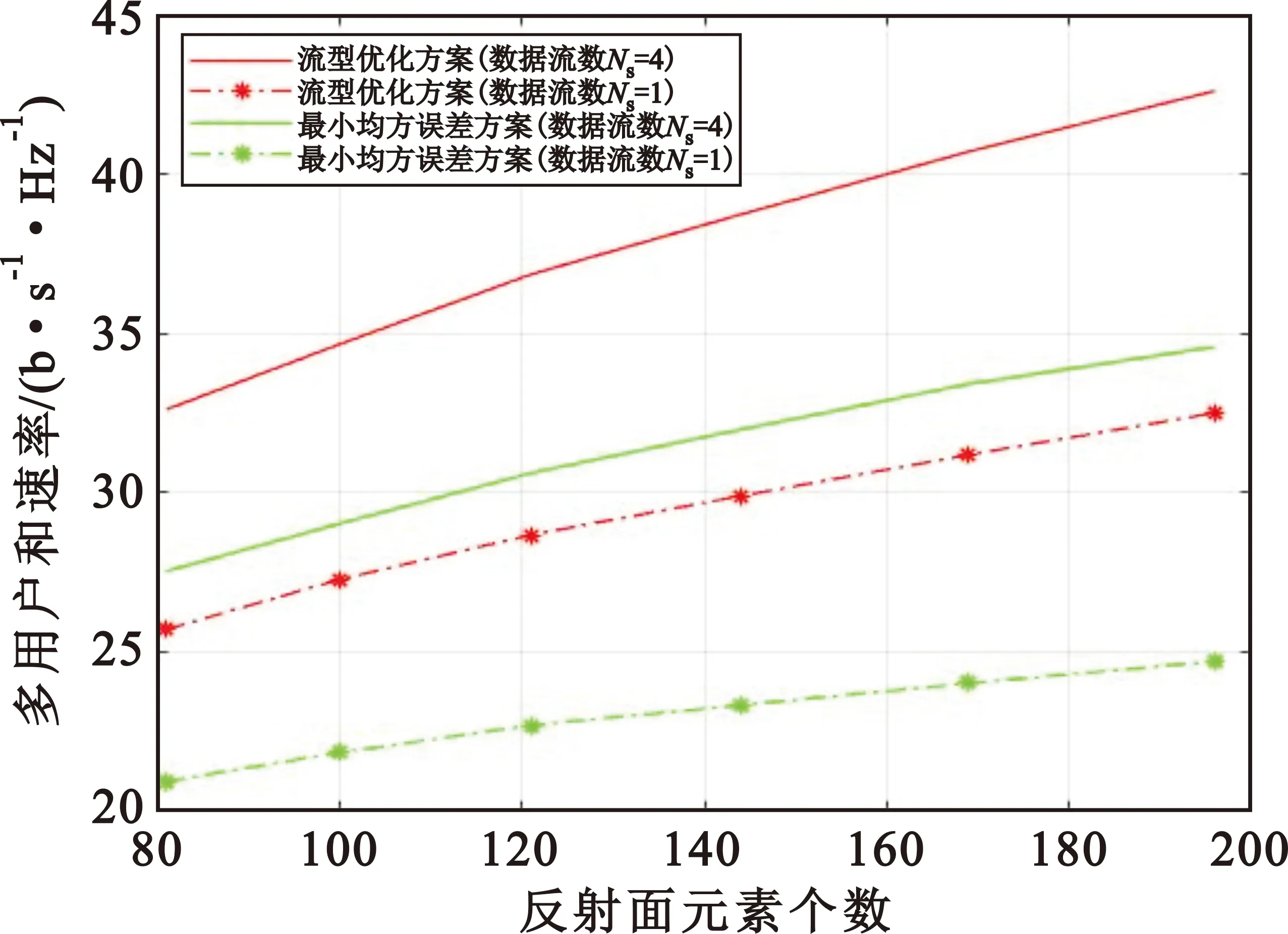
图4 智能反射面辅助的毫米波MIMO系统多用户和速率与反射面元素个数之间的关系
4 结 论
本文考虑了一个基于智能反射面辅助的毫米波MIMO系统,优化目的是通过协同优化智能反射面的无源波束成形、功率分配、预编码矩阵以及合并矩阵来最大化多用户和速率。当基站至用户的直连链路被阻塞时,采用了一种基于智能反射面的流形优化设计方案。仿真结果表明,与最小均方误差方案以及随机相位方案相比,本文所采用的流形优化算法方案在多种情况下都能明显获得更好的性能,而且计算复杂度也相较于最小均方误差方案更低。
