高中数学课堂中对学生“直观想象”核心素养的培养

王来虎

（合肥市巢湖市第四中学 安徽巢湖 238000）

新一轮教学改革指出，学生的教育不仅要注重知识的教学，同时还要充分认识到培养学生学科素养的重要性，帮助学生高效地掌握知识以及身心的全面发展。直观想象是高中数学六大核心素养之一，指的是通过对空间物体的几何直觉和对物体形状的认识能力，并运用对图形的直观理解来解决问题。直觉想象是解决几何问题的一种基本能力，也是是对问题进行深入分析的一种有效方法，是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础。直观想象主要表现为：建立形与数的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物。基于立德树人的使命，直观想象力的培养事关学生数学直觉的形成以及学生数学思维的培养。从现有的教学实践出发，笔者认为，针对学生直观想象力的培养，应当在教学中渗透数学定义、空间几何以及解析结合等方面的内容。

一、定义教学与直观想象的培养

从中学数学教材的特点来看，往往通过“定义”的方式来进行数学概念的引入，随后应用推理归纳等思维方法，探讨相关概念的本质属性，在充分理解概念的基础上应用所学习的数学概念解决数学问题。然而，很多数学概念都是比较抽象的，理解起来也很困难，我们经常会借助一些“几何”手段来理解概念，将复杂、抽象的概念变得简明形象，让学生直观感知概念的本质属性。

例如，必修1教材在函数单调性性质研究时，给出增减函数的定义：一般地，设函数f（x）的定义域为I，D⊆I，任意x1，x2∈D，如 果x1＜x2都 有f（x1）＜f（x2）（f（x1）＞f（x2）），那么就说函数f（x）在区间D上是单调递增（递减）函数。如何理解增函数的定义？学生就要理解定义中x1，x2任意性的，它表示的是区间D上的所有的自变量，而不是某两个特殊值，这也体现初中的数学思维和高中的数学思维很大的不同，有着很大的跨越，所以高一学生在理解增函数的概念时就会很困难，教学中发现了很多学生就只通过两个特殊的x1，x2得到了函数的增减性。函数单调性的本质是反映了函数值随着自变量x变化而变化的一种趋势，因此在教学过程中，教师可以借助函数的图像帮助学生理解函数单调性的概念，若f（x）是区间D上的增函数，则图像在区间D上的部分从左到右是呈上升趋势的，若f（x）是区间D上的减函数，则图像在区间D上的部分从左到右是呈下降趋势的，利用函数的图像，让函数的单调性动起来了，也更加形象、更直观、更生动，学生也更加容易理解。

数学概念是数学思维和数学思想的重要载体，是发挥直觉思维能力的主要途径。在实施教学的过程中，教师要自觉引导学生应用直观思维理解抽象概念，从而使得抽象概念具象化。

二、立体几何教学与直观想象的培养

人本身就生活在三维空间里，立体几何这门课程对于帮助学生认识我们生活的世界具有很大的现实意义，而直观想象能力又是学生学好几何的关键。立体几何的主要教学目标来看，就是要逐步培养学生的空间观念，引导学生灵活应用几何直观以及空间想象来更好地感知事物的空间变化。并熟练应用数形语言来表达物体的空间关系，从而帮助学生更好地认识几何体的结构特征，确保学生具有在平面空间绘制几何图形，并对几何图形进行分解的能力。因此，通过立体几何的教学发展直观想象核心素养是恰当适宜的。

在立体几何的教学活动中，组织学生观察棱柱、棱锥、棱台、圆柱、圆锥、圆台以及球这些几何体，学生能够很好地了解各种几何体的特点，以及几何体之间的区别。例如学生通过观察棱柱，总结出棱柱的结构特征：有两个面是互相平行的，并且每相邻两个四边形的公共边都相互平行；观察圆柱后可得到圆柱也有两个面互相平行，但它的侧面是曲面，而不是四边形，这样学生通过观察几何体，对这两种几何体有了更全面的认识，并且也能找到他们之间的不同点。除了观察几何图形以外，我还要求学生动手去做几何模型，陶行知先生就教导我们要在学中做，在做中学，所以在学生学完多面体和旋转体之后，我就开展了一个活动：多面体和旋转体模型制作比赛，学生们参加的热情非常高，也制作出很多精美的几何体模型。通过比赛不仅能让学生动手实践，在实践中体会空间点线面的位置关系，而且这些模型也可以为我们后面的教学提供了教具。同时，我们还要善于利用身边的实物模型进行课堂教学，比如课本，随意翻开课本就是一个很好的二面角模型，通过课本的展开可以研究二面角的范围变化；教室门的开关与闭合可以演示线面平行的判定，也可以演示线面垂直的判定。因此，在立体几何的课堂教学和学生的学习中，要有意识地灌输和利用这种思想，对培养学生的直观想象能力起到很好的效果。

实物模型对帮助学生认识几何图形、发展空间想象能力提供了一定的帮助，但在学习空间的点线面的位置关系、解决空间几何证明题的时候，我们还是要借助直观图。直观图是发展空间想象力的关键，在立体几何部分教学时，我就加强训练学生能根据实物画出直观图形，由直观图能想象出实物的空间位置，表达出图形各部分的位置关系及度量关系。同时，在教学过程中如果要画几何体直观图时，我都是按照画图的准则，做好示范，让学生真正掌握画图直观图的方法和要领，并且努力培养学生动手画图的能力。

三、解析几何教学与直观想象的培养

解析几何也是培养学生直观想象能力的一大阵地，充分挖掘解析几何的内容，精心设计教学，对发展学生的直观想象能力是十分有效的。

圆锥类的问题是动态问题，在平面分析几何中，动态问题无处不在。对动点、动线、动曲线等动态问题的求解，要求学生具有良好的空间想象力。需要学生在脑海中生成一幅动态图，再绘制一幅简单的平面图，并利用相关的曲线知识进行求解；也可以在脑海中把一些固定的图形变成一个动态的图形。无论从普通到特别，或者特别到普通的思维方式，都无法在纸上描绘，必须要实现在思维中，需要学生充分的发挥自身的直观想象力。

例1.设圆x2+y2+2x-15=0的圆心为A，直线l过点B（1，0）且与x轴不重合，l交圆A于C、D两点，过B作AC的平行线交AD于E.证明|FA|+|BE|为定值。

解析：如图，因为|AD|=|AC|，BE/CA故∠EBD=∠ACD=∠ADC，所以|BE|=|DE|又圆A的标准方程为（x+1）2+y2=16，从而|AD|=4,所以|FA|+|BE|=4为定值。

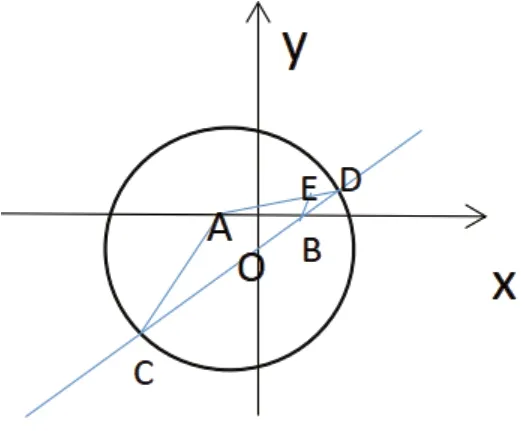
本例中点C、D是圆上动点，引出动点E且其轨迹为椭圆。作出图形的同时，应当能想象其动态过程，结合平面几何的知识（圆的性质，平行的性质）在简单的运算中使命题快速得证，充分彰显了几何直观的魅力。

四、数形结合教学与直观想象的培养

数形结合数学思想关键在于数字与图形之间的相互转化，其本质是把抽象的数值与直观的图形相融合，建立起抽象思维与形象思维之间的联系，通过几何的方法去研究数字的关系或者利用数字的关系来表达图形的变化，从而对数字以及图形的性质进行充分解析，充分利用直觉想象力来建立起数字与图形之间的联系，将抽象的观念与具体的形象、表象进行连接与转换，由抽象变为直观，使得一个繁复的问题变得简单明了。“数”是对“形”的抽象化，而“形”则是对“数”的一种直接表达。所以，数字与形体之间的关系并不单纯是一种连接，而是一种数学思想、数学思维，它让解题更加简单、好玩。

在数学解题过程中，我们经常将一些代数问题几何化，利用几何直观形象的特点帮助我们解题，充分挖掘好数形结合问题，把数的问题图形化，形象化，这对学生直观想象能力的提升是有帮助的。

华罗庚教授说过：“数缺形时少直观，形少数时难入微。数形结合百般好，隔离分家万事休。”数形结合是一种对数与形之间的化归与转化的意识，这种对数的认识与运用的能力，是培养直观想象核心素养所必需要的。

在高中数学教学中，培养直观想象素养还须注重“自然性”，从平面到空间，从数到形，不是一个过渡而是一次飞跃，是自然而然的质变。随着课程改革的逐步实施，为能让数学核心素养在课堂教学活动中得以实现，需要对教学内容进行细致的分析，并针对性的对学生的直观想象能力进行培养，特别是在几何题作答的过程中，教师需要做好基础知识的夯实，然后给学生渗透直观的空间意识。总之，直观想象素养的培养不是一朝一夕的事情，我们在教学中要结合教材内容精心设计，认真研究，充分准备才能起到良好的效果。