基于电网考核指标的火电机组一次调频仿真与优化
2023-01-17于海存殷建华李荣丽郭瑞君霍红岩
于海存,殷建华,李荣丽,郭瑞君,霍红岩
(内蒙古电力(集团)有限责任公司内蒙古电力科学研究院分公司,呼和浩特 010020)
0 引言
火力发电机组的一次调频性能对电网的电能质量和安全运行水平起着至关重要的作用。随着新能源发电量占比的逐步提高,电网对火电机组的一次调频要求越来越高[1-2]。2020年3月内蒙古电网开始正式考核一次调频指标,新的考核办法着重考查机组的“15 s出力响应指数”“30 s出力响应指数”和“电量贡献指数”三项指标,这与原一次调频考核指标有很大的区别[3]。根据考核情况反馈,内蒙古电网火电机组一次调频动作综合合格率仅在20%左右,亟需提升一次调频考核指标和改善网内火电机组一次调频性能。目前,国内对火电机组一次调频功能的优化方式有两种:一是采用单一的逻辑组态优化,该种优化方案成本低、针对性较差,优化效果不稳定,可推广性较差;二是利用储能辅助一次调频,该技术方案成本投入较大,且频繁充放电对电池的寿命及容量损耗较大,增加了环境污染的风险性[4-6]。本文提出基于电网考核指标的火电机组一次调频综合优化技术,以一次调频考核指标为数据支撑,利用人工智能算法优化信号测量、逻辑运算、执行系统和控制调整等各环节。
1 一次调频考核指标
1.1 定义
1.1.1 出力响应指数
出力响应指数为从频率偏差出死区开始至频率偏差恢复到死区范围结束,一次调频动作时段内机组实际最大出力调整量占理论最大出力调整量的百分比,计算见公式(1)—(3)。机组一次调频的负荷调整幅度应在15 s内达到理论计算的一次调频的最大负荷调整幅度的75%,在30 s内达到理论计算的一次调频的最大负荷调整幅度的90%[7]。
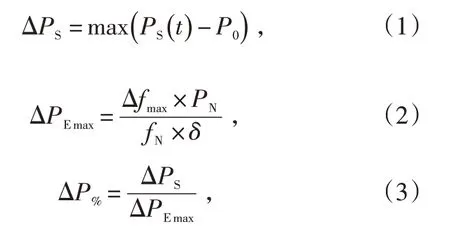
式中:ΔPS为一次调频实际最大出力调整幅度,kW;ΔPEmax为机组一次调频理论出力最大调整量,kW;ΔP%为一次调频出力响应指数;P0为电网频率变化越过机组一次调频死区时刻机组的实际出力,kW;PS(t)为一次调频机组在t时刻的实际出力,kW;PN为机组额定有功出力,kW;Δfmax为一次调频动作时段内考虑到调频死区的实际最大频率偏差,Hz;fN为机组额定频率,取50 Hz;δ为转速不等率理论整定值,火电机组一般取0.05。
1.1.2 电量贡献指数
电量贡献指数为在机组一次调频动作时段内,机组一次调频实际贡献电量占理论贡献电量的百分比,计算见公式(4)—(7)。从频率偏差超出死区开始,直至频率偏差恢复到死区范围结束,机组实际贡献电量需达到理论贡献电量的75%,否则机组一次调频判定为不合格[7]。
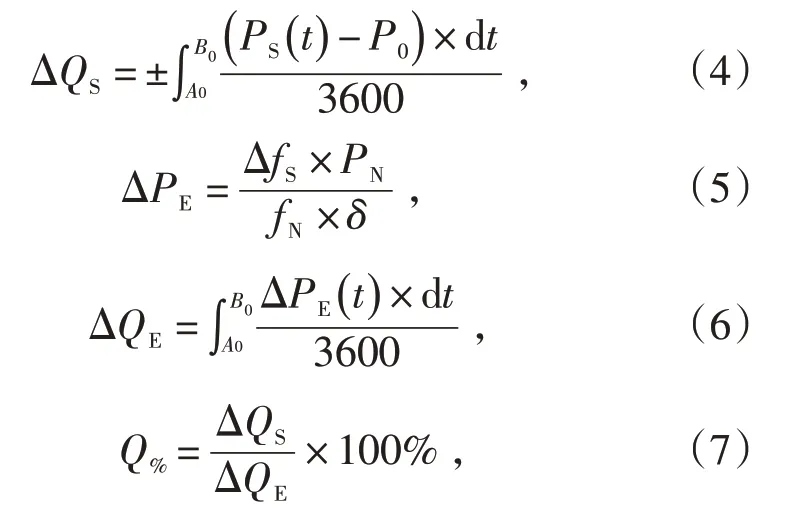
式中:ΔQS为机组一次调频实际贡献电量,kWh;ΔPE为机组一次调频理论出力调整量,kW;ΔfS为一次调频动作时段内实际频率与调频死区(50±0.033 Hz)的频率偏差,Hz;ΔQE为机组一次调频理论贡献电量,kWh;Q%为机组一次调频电量贡献指数。
1.2 存在的问题及建议
1.2.1 存在的问题
参考出力响应指数的定义和公式,15 s出力响应指数和30 s出力响应指数的合理性值得商榷。原因是如果公式(2)中ΔPEmax对应的Δfmax发生在一次调频动作30 s后,那么该次一次调频动作15 s内以及动作30 s内都无法获知ΔPEmax的大小,在这种情况下要求动作15 s内以及30 s内的ΔPS分别达到ΔPEmax的75%和90%显然不合理。
举例说明。如图1所示,14:11:14,电网一次调频持续动作时间在60 s以上,一次调频动作考核期间频率极值点为49.958 Hz,发生时刻为14:11:57,即一次调频动作43 s。一次调频动作考核期间前15 s内频率极值点为49.963 Hz,一次调频动作考核期间前30 s内频率极值点为49.960 Hz。以300 MW火电机组为例计算,此次一次调频考核期间理论最大出力调整量为1.08 MW,而实际上前15 s内理论最大出力调整量仅为0.48 MW,前30 s内理论最大出力调整量仅为0.84 MW。即使该机组能够完全按照理论值调整功率,计算得到的15 s出力响应指数仅为44.44%,30 s出力响应指数为77.78%。结合图2以某300 MW机组同时刻实际一次调频动作数据为例,电网考核计算的该机组15 s出力响应指数50.542%,30 s出力响应指数80.503%,即两个指标都不合格。而该机组实际的15 s内最大出力调整量为0.545 MW,为15 s内理论最大出力调整量的113.7%;实际的30 s内最大出力调整量为0.869 MW,为30 s内理论最大出力调整量的103.4%。在这种情况下,即使机组规定时间内功率调整量大于理论值,30 s出力响应指数和15 s出力响应指数这两个一次调频考核结果仍然不合格。
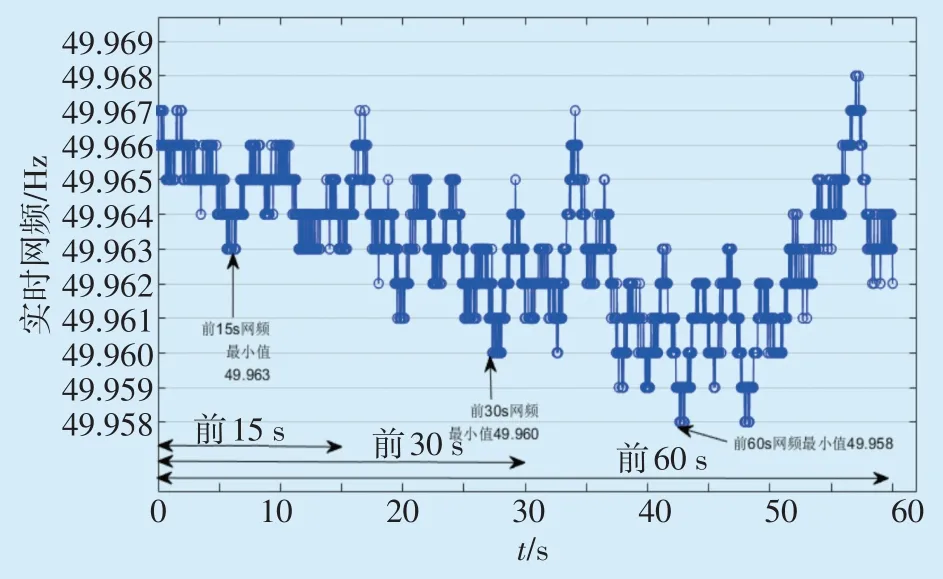
图1 一次调频动作期间电网频率曲线Fig.1 Grid frequency curve during primary frequency modulation
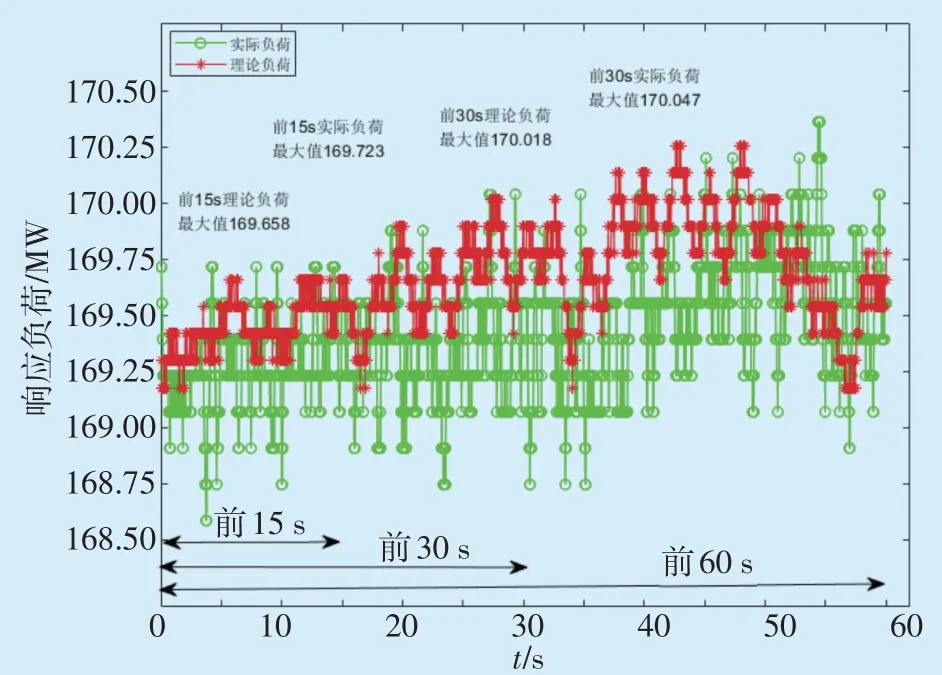
图2 一次调频动作期间机组响应负荷曲线Fig.2 Unit response load curve during primary frequency modulation
1.2.2 合理建议
当某次一次调频考核动作期间频率极值点出现在15~60 s,计算15 s出力响应指数的公式(3)中分母应改成15 s内的理论最大出力调整量;当某次一次调频考核动作期间频率极值点出现在30~60 s,则计算30 s出力响应指数的公式(3)的分母应改成30 s内的理论最大出力调整量。
2 基于极限学习机算法的一次调频性能分析与优化
2.1 方法思路
本文利用人工神经网络极限学习机(Extreme Learning Machine,ELM)算法搭建一次调频性能考核指标与相关影响因素的映射模型,以火电机组一次调频性能考核指标的结果数据作为输出层变量,选取多个可调可控的一次调频影响因素作为研究和分析对象,并从调度中心数据库以及发电机组历史数据库中提取相对应的特征量作为输入层变量,并在此基础上训练人工神经网络模型系统参数使之达到符合要求的拟合及预测精度。再通过对考核指标不合格的一次调频动作事件所对应的输入层特征变量的适度变异,使得经神经网络算法搭建的系统模型重新计算后一次调频考核结果由不合格变为合格。特征变量适度变异的变化方向和程度即可为一次调频性能优化提供指导依据。
2.2 方法步骤
方法步骤如图3所示,主要包括获取输入输出数据、搭建模型训练模型参数、变异输入变量重新计算以及反推优化策略等。
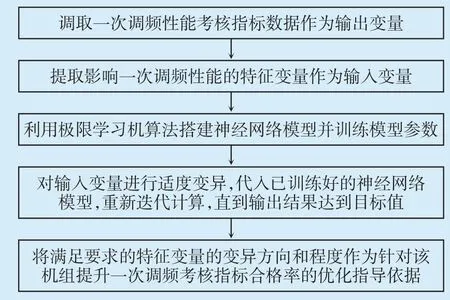
图3 算法流程Fig.3 Flow chart of algorithm step
2.2.1 获取输出数据
从电网调度中心系统数据库中调取一次调频性能指标考核数据,包括15 s出力响应指数、30 s出力响应指数、电量贡献指数。
2.2.2 获取输入数据
从电网调度中心服务器数据库中调取火电发电机组同步相量测量(PMU)子系统上传的运行数据,包括有功功率、频率、转速、机组调节级压力、协调控制系统中一次调频修正前负荷指令、协调控制系统中一次调频修正后负荷指令、阀门开度信号、一次调频动作信号、一次调频投入信号、机炉协调信号。
从对应火电发电机组分散控制系统(DCS)和数字电液控制(DEH)系统历史数据库中调取机组相关运行数据,包括主蒸汽压力、主蒸汽流量、高压调节阀开度指令、高压调节阀开度反馈等。
根据火电机组一次调频常规动态试验的试验过程和调整手段,影响一次调频性能考核指标的因素较多,但影响效果显著且可调可控的因素主要有机组主蒸汽压力、机组转速不等率、机组阀门流量特性线性度、机组机组感应频率与电网基准频率偏差、机组自动(AGC)调节指令[8-9]。
发电控制提取能表征一次调频考核指标性能影响因素的特征变量。
(1)网频偏差特征变量c1:

式中:Δf为机组实际测量的网频变化量,Hz。
网频偏差特征变量c1变异值约束范围:
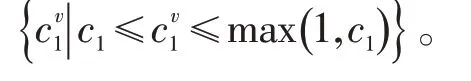
(2)AGC指令特征变量c2:

式中:Plb为协调控制系统中一次调频修正前负荷指令,kW。
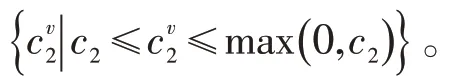
(3)主汽压力特征变量c3:

式中:PTa为一次调频动作期间实时主汽压力均值,MPa;PTN为机组主汽压力额定值,MPa。
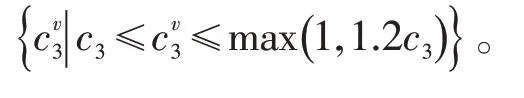
(4)调节阀流量特性特征变量c4表征一次调频考核期间机组流量指令所在区间内的相对流量比值:

式中:ΔS为上述区间段内实际主汽流量的变化量,t/h;Se为机组额定主汽流量,t/h;ΔSl为上述区间段内流量指令的变化量,%。

(5)转速不等率特征变量c5:
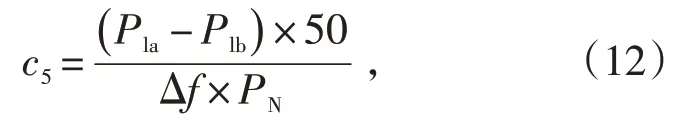
式中:Pla—协调控制系统中一次调频修正后负荷指令,kW。
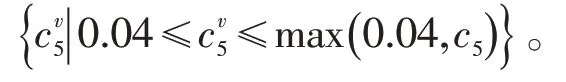
2.2.3 搭建模型训练模型参数
ELM算法是一种新型的快速学习算法,网络训练模型见图4。对于单隐层神经网络,ELM算法可以随机初始化输入权重和偏置并得到相应的输出权重。该算法仅通过一步计算即可解析求出学习网络的输出权值,极大地提高了网络的泛化能力和学习速度[10]。设m,M,n分别为网络输入层、隐含层和输出层的节点数,g(x)是隐含层神经元的激活函数,bi为阈值。设有N个不同样本(xi.ti),1≤i≤N,其中,表示连接网络输入层节点与第i个隐含层节点的输入权值向量;表示连接第i个隐含层节点与网络输出层节点的输出权值向量。
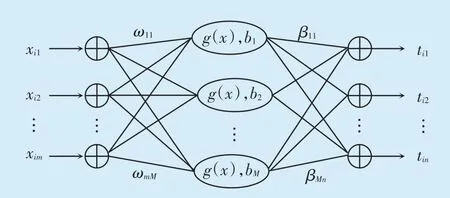
图4 极限学习机的网络训练模型Fig.4 Network training model of extreme learning machine
2.2.4 变异输入变量重新计算
在合理范畴内逐一“变异”单个特征变量,代入上节训练完成的神经网络模型重新迭代计算。
2.2.5 反推优化策略
在上一步的基础上根据满足要求的特征变量的变异方向和程度,对一次调频性能考核指标不合格的原因进行逆向分析,继而提出针对性的改善和提升策略。
3 仿真分析
3.1 仿真
综上,以500组主蒸汽压力、机组转速不等率、机组阀门流量特性线性度、机组感应频率与电网基准频率偏差、机组AGC调节指令五个特征变量为输入变量;以对应的500组一次调频性能指标考核中的15 s出力响应指数、30 s出力响应指数、电量贡献指数分别为输出变量;结合ELM算法搭建学习训练模型,其中分别选择sigmoid正切函数、sin正弦函数、hardlim硬限幅函数三种代表性激活函数以及不同的隐含层节点数进行组合分别仿真,其中随机300组数据用于仿真拟合训练,剩下的200组数据用于仿真预测。
仿真结果如图5—图7所示,隐含层节点相同前提下,sigmoid正切函数的整体仿真效果最好,且三种激活函数在隐含层节点数为30左右就已经达到各自的最佳仿真精度。因此最终选择隐含层节点数为30,激活函数为sigmoid正切函数作为模型的参数。为进一步验证算法的有效性,将该模型参数下的ELM算法与以最小二乘法为原理的线性回归算法(Linear Regression Algorithm,LRA)进行对比。计算并统计两种算法仿真结果的均方误差数据见表1,平均绝对误差数据见表2。
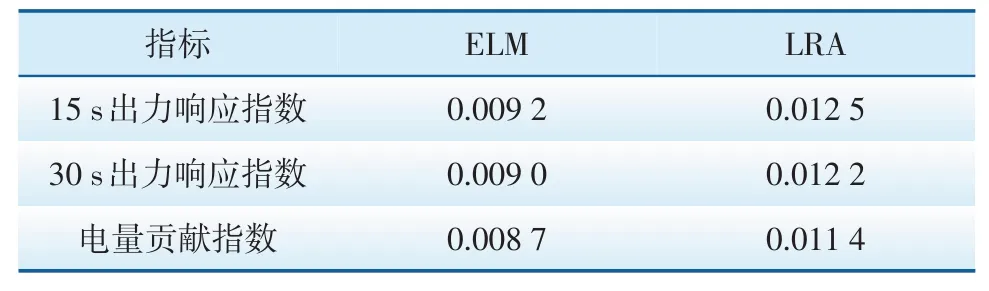
表1 两种算法均方误差数据Tab.1 Performance comparison of mean square error of two algorithms
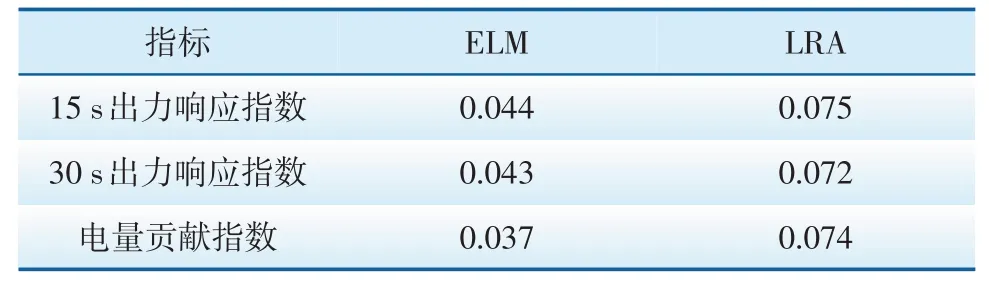
表2 两种算法平均绝对误差数据Tab.2 Performance comparison of mean absolute error of two algorithms
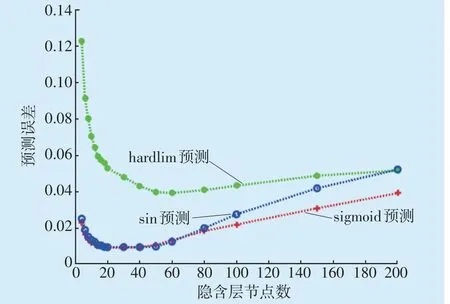
图5 15 s出力响应指数仿真参数及误差Fig.5 Simulation parameters and deviation of 15 s contribute response index
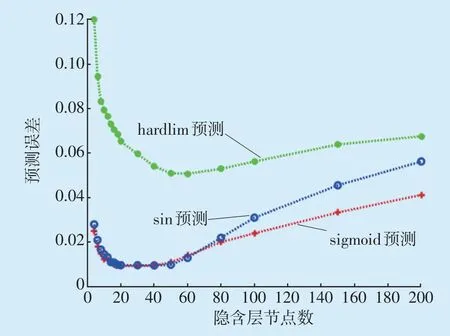
图6 30 s出力响应指数仿真参数及误差Fig.6 Simulation parameters and deviation of 30 s contribute response index
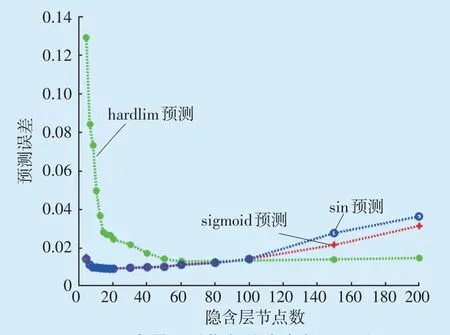
图7 电量贡献指数仿真参数及误差Fig.7 Simulation parameters and deviation of electricity contribution index
由仿真数据可知,ELM算法仿真误差小于LRA仿真误差,仿真效果优于LRA。
将各个特征变量依次变异至限制值后,代入模型中重新计算,结果见表3。
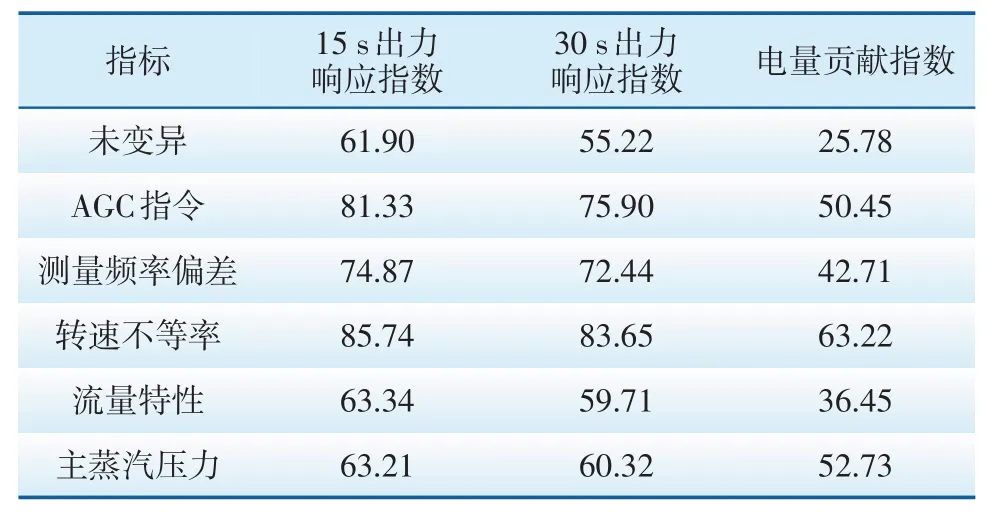
表3 特征变量变异后考核指标合格率Tab.3 Qualification rate of assessment index after variation of characteristic variables %
3.2 仿真结果分析与反推优化策略
分析仿真试验结果数据可以得出,对于该机组自动增益控制(AGC)指令、频率偏差及转速不等率所对应的特征变量变异对一次调频考核指标影响作用较大。其中如降低机组转速不等率为4%,则能够使三个考核指标合格率平均提升29.90%;在一次调频动作期间,如增加反向闭锁AGC指令的功能,能够使三个考核指标合格率平均提升21.59%;如增设高精度频率测量装置,使得机组实际响应网频与电网考核基准网频一致,则能够使三个考核指标合格率平均提升15.70%。主蒸汽压力变异对电量贡献指数影响作用较为显著,对15 s出力响应指数、30 s出力响应指数影响作用有限。且由于该机组在大修后做过流量特性修正试验(流量特性良好,指令与实际流量基本呈现线性),因此流量特性特征变量变异对机组一次调频性能考核指标作用不明显。因此针对该机组,可以根据机组自身情况从增设高精度频率测量装置、增加AGC反向闭锁功能以及适当降低转速不等率方面入手来优化一次调频功能。
4 结语
通过对一次调频考核指标的定义、公式以及实际考核结果的分析,针对15 s出力响应指数和30 s出力响应指数的考核计算公式在特定情景下提出了更为合理性的修改建议;通过仿真试验和数据分析发现:利用ELM算法搭建的神经网络模型可以在一次调频考核指标与影响一次调频性能的影响因素之间建立良好的非线性映射。根据特征变量的变异方向和程度,对一次调频性能考核指标不合格的原因进行逆向分析,并在此基础上提出针对性的改善和提升策略,指导机组进行一次调频优化。
