薄区域上随机Ginzburg-Landau方程的稳态测度极限行为①

钟文虎，陈光淦，张元元

四川师范大学 数学科学学院/可视化计算与虚拟现实四川省重点实验室， 成都 610068

Ginzburg-Landau方程是研究不稳定波理论， 描述超导现象的重要模型， 最初由Ginzburg等[1]在刻画超导相变时导出. 该方程应用广泛， 例如模拟色散波在流体力学等物理领域的传播[2]， 也应用于光学、等离子体物理、化学反应[3]等.

本文研究三维薄区域Dε上由白噪声驱动的随机Ginzburg-Landau方程

(1)

(2)

文献[4]证明了二维有界区域上的随机Ginzburg-Landau方程的遍历性和指数混合性. 文献[5]推广了文献[4]的结果， 当有界区域的维度小于或等于4时， 证明了随机Ginzburg-Landau方程的遍历性， 并且得到了稳态测度的指数估计. 最近几年， 文献[6-8]系统地研究了随机Ginzburg-Landau方程的遍历性与指数混合性. 关于稳态测度的极限行为， 文献[9]运用区域均值化投射算子， 证明了三维随机Navier-Stokes方程的稳态测度收敛于二维随机Navier-Stokes方程的稳态测度.

本文的目的是将文献[9]的研究工作推广至方程(1). 由于投射算子改变了方程(1)的结构， 因此难以保证投射算子作用后的方程(1)仍然具有耗散性质， 这导致稳态测度的极限行为不易由能量估计获得. 通过弱收敛估计， 得到方程(1)的稳态统计解的收敛结果， 然后将收敛性质转化到稳态测度上， 最终获得了方程(1)的稳态测度的极限行为： 当ε趋近于0时， 方程(1)的稳态测度收敛于二维区域上随机Ginzburg-Landau方程的稳态测度； 进一步地， 当ε，υ同时趋近于0时， 方程(1)的稳态测度收敛于二维区域上非线性Schrödinger方程的稳态测度.

本文结构如下， 第一节描述三维薄区域上的随机Ginzburg-Landau方程模型， 给出适定性与遍历性. 第二节给出二维区域上随机Ginzburg-Landau方程和非线性Schrödinger方程的适定性与遍历性. 第三节呈现方程(1)稳态测度的两类极限行为.

1 薄区域上的随机Ginzburg-Landau方程

1.1 空间设置

嵌入Y⊂X是紧的[10].

1.2 白噪声与统计解

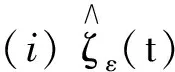
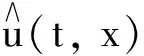
(3)

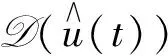
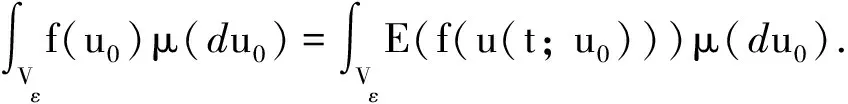
1.3 适定性与遍历性

引理1[5，10]设u0是一个Vε值的随机变量， 与ζε(t)相互独立，且满足E(h0(u0))<∞，E(h1(u0)) <∞，B1<∞，B2<∞， 则对于任意的T>0， 下列结论成立：

(4)

(5)

引理2若引理1中的假设条件都满足， 则下列结论成立：

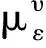
(6)

(7)

证设u为方程(1)的解， 对h1(u)使用It公式，

于是

(8)

其中C=B1+3B0B2， 独立于ε和υ.

2 极限系统

2.1 二维区域上的随机Ginzburg-Landau方程

二维区域上的随机Ginzburg-Landau方程

(9)

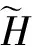
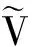
(10)

(11)

(12)

(iii) 若存在正整数n， 使得对于所有的1≤|j|≤n都有bj≠0， 则方程(9)的稳态测度唯一存在；

(13)

2.2 非线性Schrödinger方程

给出二维有界区域D上的非线性Schrödinger方程

∂tv-iΔv+iλ|v|2v=0

(14)

和三维薄区域Dε上的非线性Schrödinger方程

∂tu-iΔu+iλ|u|2u=0

(15)

由于λ>0， 方程(14)和方程(15)的解唯一存在[13].

引理5[13]若初值u0∈Vε， 满足h0(u0)<∞，h1(u0)<∞， 则方程(15)存在稳态测度με和稳态解uε(t，x)， 且με=D (uε(0)).

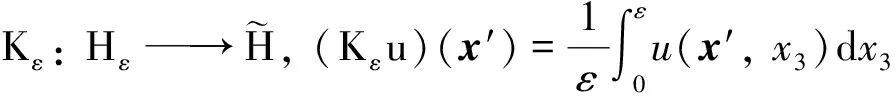
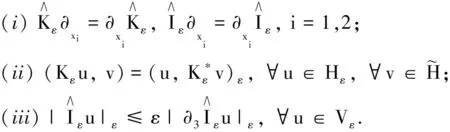
3 稳态测度的极限行为

3.1 区域投射极限

定理1若引理1与引理3中的假设条件都成立， 且极限

(16)

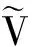
(17)

(18)

下面分别证明Pυ是方程(9)的稳态统计解，μυ是方程(9)的稳态测度.

(19)

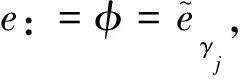
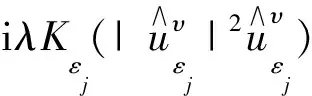
(20)

运用Hölder不等式和Young不等式得

(21)

(22)

(23)

(24)

(25)

其中

(26)

(27)

唯一性由引理3给出.

3.2 粘性消失极限

(28)

(29)

(30)

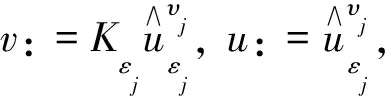
S2： =|((i+υj)KεjAεu-iAv，e)|=|(υjv，e)|≤υjCe‖v‖D

(31)

(32)

结合(23)，(31)和(32)式得

(33)

运用Chebyshev不等式， 结合(4)，(8)，(10)，(11)和(33)式得， 对于任意的δ>0有

(34)

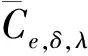
(35)

其中

接下来， 使用定理1中的方法， 由(35)式推出结论(i)和结论(ii)成立.

通过(34)式知， 在取极限的过程中，εj和υj相互独立. 于是， 使用定理1中的方法， 并在形式上重复定理1的证明过程， 结合(6)，(7)，(12)和(13)式得到下列收敛结果：

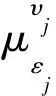
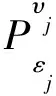
其中，μεj和uεj(t)分别是方程(15)的稳态测度和稳态解， 故结论(iii)成立.