基于贝叶斯优化模型的涡轮增压4缸发动机故障诊断

单家正

（安庆职业技术学院机电工程学院，安徽 安庆 246003）

0 引言

为满足日益严格的设计要求，发动机在最佳状态下运行是至关重要的，保持发动机在动力和速度最佳效率曲线上运行，有效降低油耗，这需要进行故障诊断来保障和实现。故障诊断可以帮助在早期阶段识别故障，减少发动机进一步损坏，从而提高车辆的安全性和可靠性。基于信号的故障诊断方法复杂程度低、易实现、适应性强，具有快速、有效的特征，能够及时进行数据反馈，因此，本研究采用基于信号的方法进行故障诊断。

基于信号的故障诊断系统主要由4个阶段组成：数据采集、信号分解、特征提取和故障状态分类［1］。传统的信号处理方法是利用时域和频域分析来区分不同的故障情况，例如，Herrera等［2］利用频域分析，包括快速傅里叶变换（FFT）、包络分析和阶次跟踪，来识别不同的运行条件和故障类型。基于FFT方法的主要缺点是不能充分地分析时间依赖的因素，而利用短时傅里叶变换（STFT）［3］、小波变换等时频分析方法可以解决这一问题。与STFT相比，小波变换具有在多分辨率时频窗口中分析信号的能力，因此，它被广泛应用于发动机的故障诊断［4-8］。本文采用小波包变换（WPT），因为它可以将信号同时转换为高、低小波系数，这对于分析不同频率范围内各种故障类型很重要［9-10］。信号分解后，可以提取出相关的时频信息，作为故障分类的输入。

现有文献中的大多数故障诊断模型遵循单一的分类算法，或试图在少数几种分类算法之间进行比较，以找到最佳的模型［11-14］。但需要注意的是，故障都有不同的特点，需要根据其对应的分类性能选择合适的算法。模型超参数的优化已经有了相当多的研究工作［15-16］。然而，现有文献中模型选择与超参数优化结合的方法有限。一种有用的方法是利用元学习过程，它利用以前数据中的信息来找到最优算法或超参数配置［17］。在许多情况下，这是不实际的，因为计算复杂性非常大。贝叶斯优化［18］是克服这一问题的适当方法，它已被证明在几个具有挑战性的基准问题上优于其他优化技术［19-20］。

贝叶斯优化的目标是利用交叉验证的分类误差找到使目标函数最小化的点［21-22］。函数评估本身可能涉及一个繁琐的过程，Sriniva等［21］通过使用主成分分析（PCA）解决了这一问题。将特征空间减少到较少的主成分，降低了计算复杂度，减少了评价时间［23-24］。PCA已经被证明在非常大的数据集中可以减少训练时间，提高分类性能［25］。文献调查发现，利用主成分分析来减少贝叶斯优化的特征集及其对优化性能的影响在很大程度上还没有得到解决。

近年来，声信号由于具有远距离测量、避免安全风险等优点，在发动机故障诊断中得到了越来越多的关注。本文通过对汽油发动机的声信号分析，提出了一种新的发动机故障诊断方法，对3种模型进行分析和比较：标准分类模型（模型1）、贝叶斯优化分类模型（模型2）、PCA结合贝叶斯优化模型（模型3）。3种模型都使用WPT进行信号分析，并从高低WPT系数中计算出统计特征。

1 试验设备和方法

1.1 汽油发动机及数据采集系统

试验使用的是1.6 L的福特ECOBOOST发动机，参数如表1所示。使用麦克风收集声音信号，由安装在距离汽缸盖1 m左右的2个Vernier MCABTA传感器完成，麦克风连接笔记本电脑的5通道数据记录仪（Labquest 2）上（图1）。声波信号也被手机捕捉到，采样频率为44.1 kHz。每个数据集包含10 s的振动信号，包含44.1万个数据点。音频采样的比特率为128 kb/s，单通道。Vision 4.1.4软件用于发动机参数的数据采集。

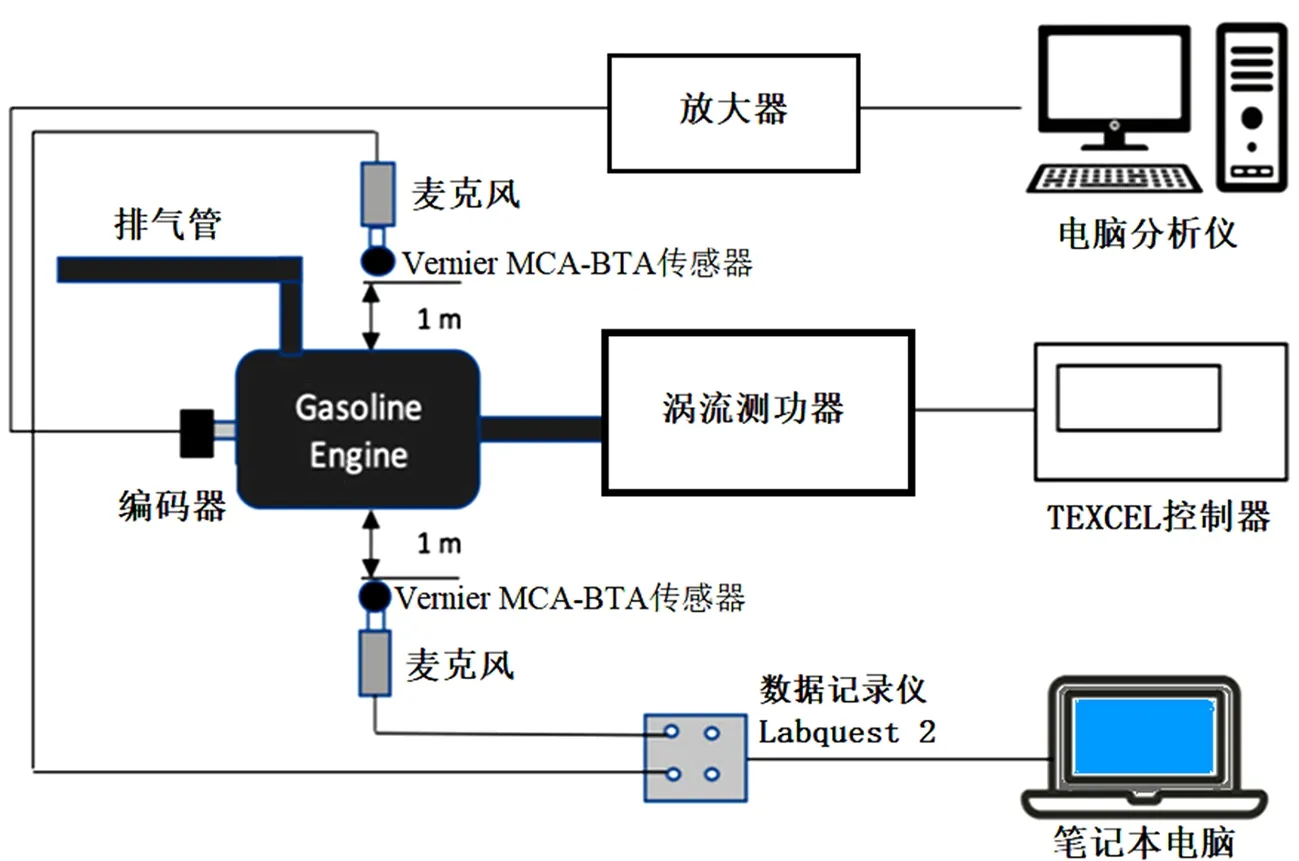
图1 声信号采集设备示意图

表1 1.6 L的福特ECOBOOST发动机参数

试验了3种类型的故障：发动机熄火、点火正时变化、空燃比（AFR）变化。每次试验都是发动机在不同的速度和加载条件下进行。AFR变化是一个关键故障，因为它可以实时调整供油脉宽和正时相位，以达到最大的效率和功率，而AFR传感器或空气流量计的损坏会导致发动机效率和功率输出下降，这是通过改变空气流量来实现的。AFR范围为10.10 ～ 17.20，理想值为14.45。试验发动机在不同工况(空转、1 750、2 250和3 000 r/min)下运行，以实现数据的多样化。各种故障工作点如表2所示。

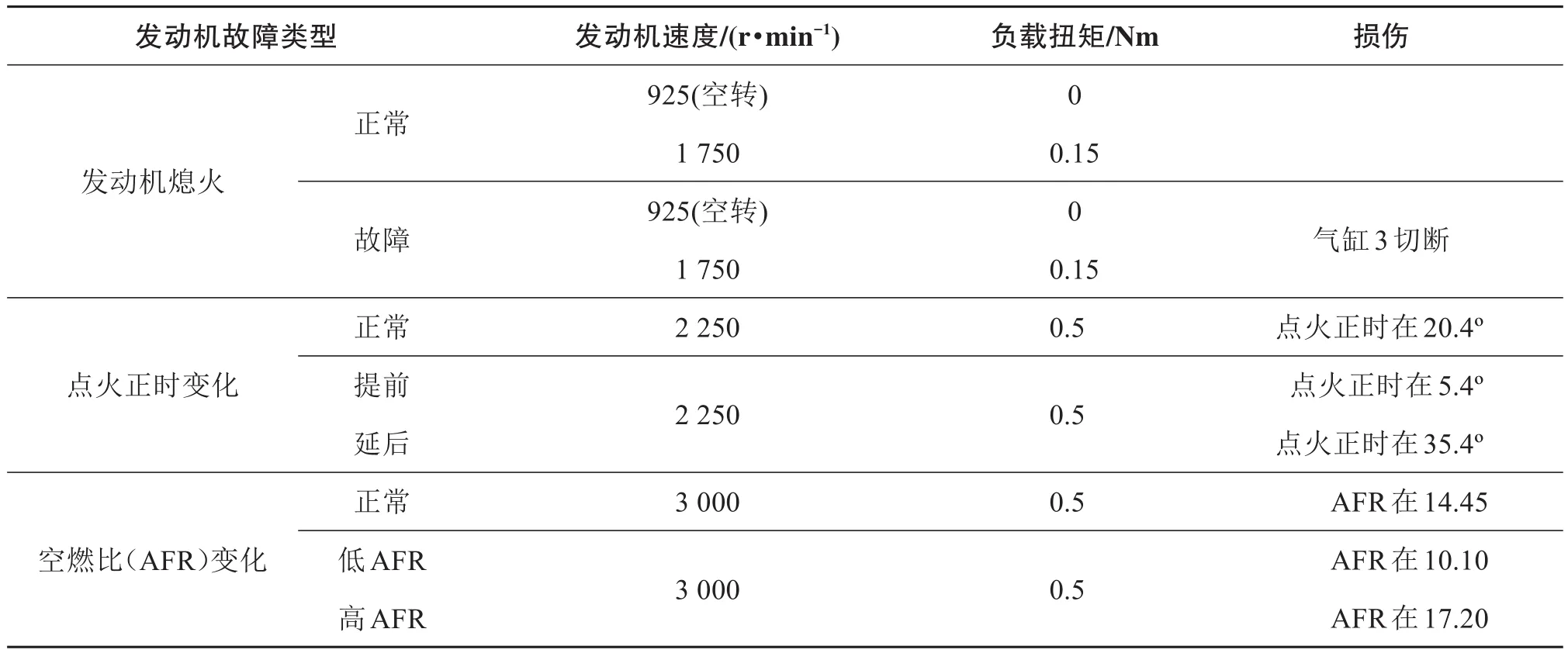
表2 故障和工作条件

1.2 试验方法

主要目标是为汽车开发和验证一个自适应故障检测和分类系统，在不同速度和操作条件下是鲁棒的。从引擎中采集声信号并进行预处理，利用小波包变换（WPT）对信号进行分解，利用小波系数的统计度量对特征向量进行特征向量处理。分析和比较3个模型：模型1使用标准分类模型；模型2采用贝叶斯优化方法进行自动分类模型选择和超参数优化；模型3利用主成分分析和贝叶斯优化方法对大特征矩阵进行降维，在降低计算复杂度和减少评估时间的同时保证了良好的精度。总流程如图2所示。

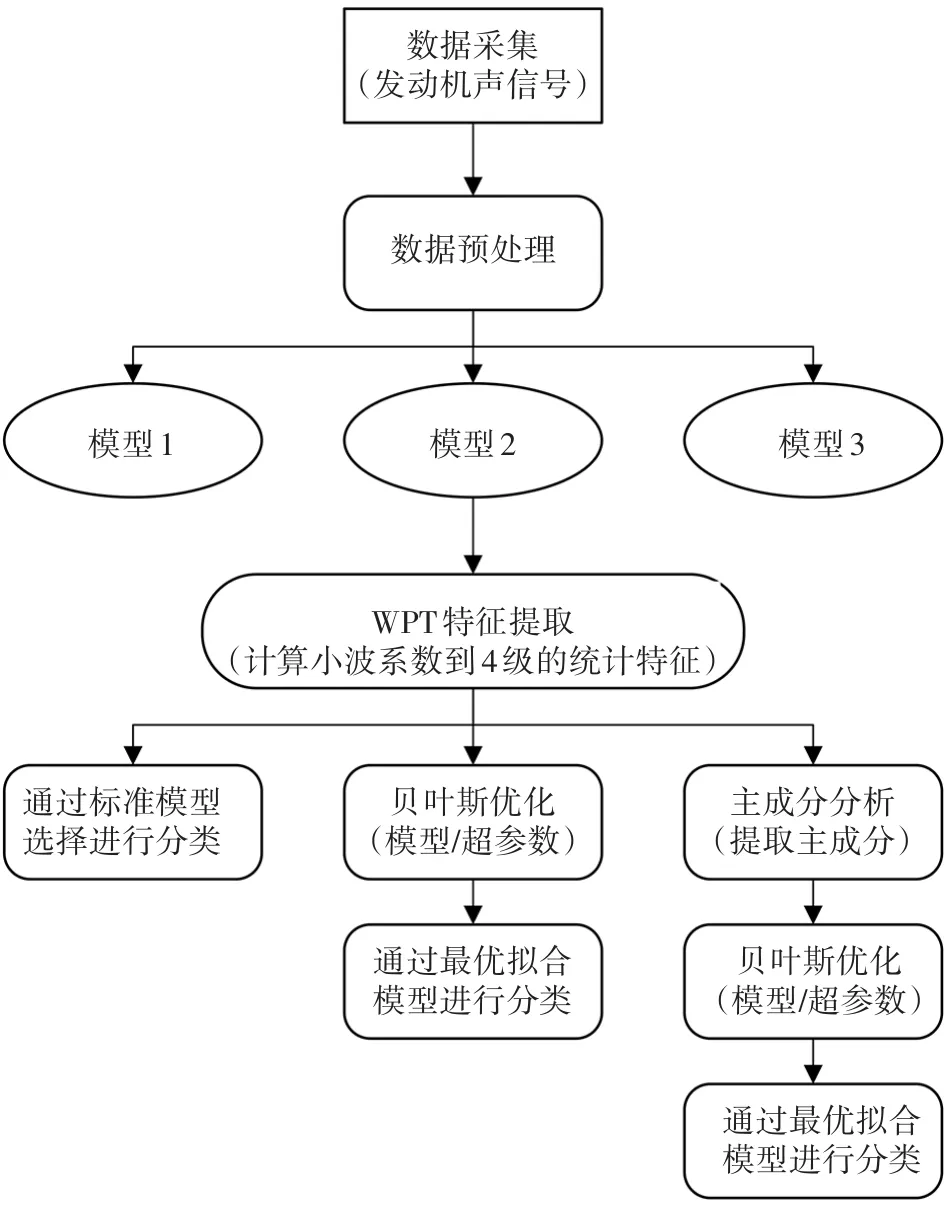
图2 总流程图

1.2.1 信号处理

发动机噪声主要包括燃烧噪声、机械噪声和气动噪声。在中低转速下，燃烧噪声是发动机噪声的重要组成部分，而在较高转速下，机械噪声占主导地位［26-27］。燃烧噪声本质上是瞬态的，它受喷射参数、火花正时和AFR的影响很大。本研究采用的时频分析方法是小波包变换（WPT），因其能够检测快速变化的振幅和相位特征［28］。Daubechies小波是变换中常用的一组正交小波，可用于分析瞬态信号，本研究使用4层的Daubechies （Db4） 小波和12 kHz的滤波频率进行进一步分析。

1.2.2 特征提取

本研究利用8个统计特征（表3）对16组小波变换系数进行特征提取。因此，对每个系数进行分解后，计算出表3中的统计特征，特征的总数是8×16 = 128。点火正时变化和AFR变化的初始数据集包含300个实例，发动机熄火的初始数据集包含200个不同工况的实例。因此，有300×128或200×128的特征矩阵。

表3 重要统计特征的描述和公式

1.2.3 主成分分析

提取的特征可以作为分类的有用输入，但大量的特征往往会导致准确性较低，执行时间较长。因此，特征空间降维技术成为必要。主成分分析是一种通过对数据协方差矩阵进行奇异值分解来计算主成分的方法。主成分是由初始特征的线性组合构造的新变量，它们在笛卡尔空间中是互相正交的，是不相关的。

PCA的关键是选择要保留的主成分的数量，这可以通过将特征按其重要性排序来实现。基于特征值进行排序，计算每个主成分的总方差的百分比。对于所有数据集，选择总方差百分比的阈值为99%，以确定最佳保留主成分数量。

1.2.4 分类算法的选择

分类算法被广泛应用于状态监测，以区分健康和故障信号。本文考虑了6种标准分类器算法：决策树［29］、朴素贝叶斯［30］、k近邻（kNN）［31］、支持向量机（SVM）［32］、判别分析［33］和集成分类［34］。

标准模型是通过使用默认参数在每个分类器中运行数据，并为每个故障案例找到最适合的模型来获得的。每种故障情况下标准模型使用的最佳拟合分类器和默认参数如表4所示。

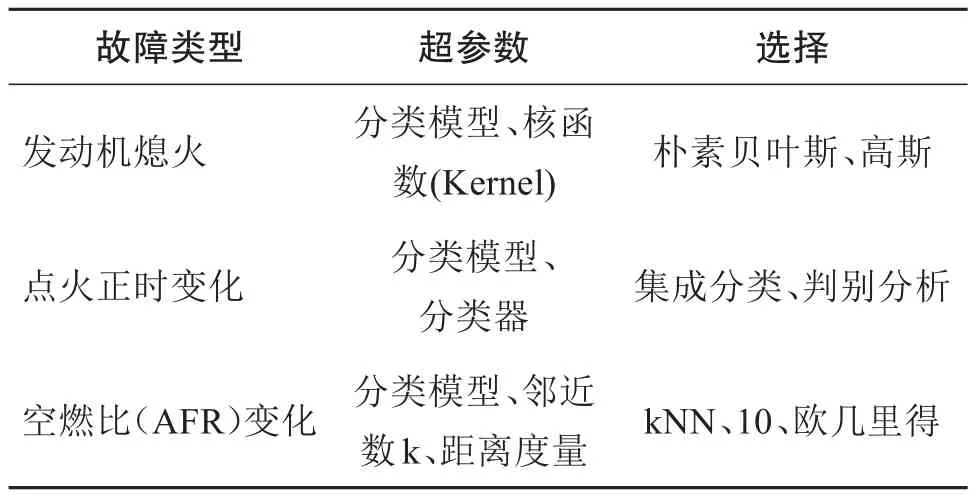
表4 模型1的最优模型参数选择

然后，通过贝叶斯优化过程确定最佳拟合算法及其最优超参数。它假设未知目标函数的样本来自高斯过程，通过使用不同的超参数进行不同的学习算法实验，得到样本的后验分布。下一个模型的超参数是通过优化预期的改进与当前结果的比较来选择的。对于众多的多峰函数，在所需的函数求值次数和时间内，这种方法已被证明是有效的，可以达到全局最优［29-30］。训练后的模型通过使用5倍交叉验证进行验证，最大迭代次数设置为180次。模型2的最佳拟合分类器及其最优参数如表5所示，模型3的最佳拟合分类器及其最优参数如表6所示。

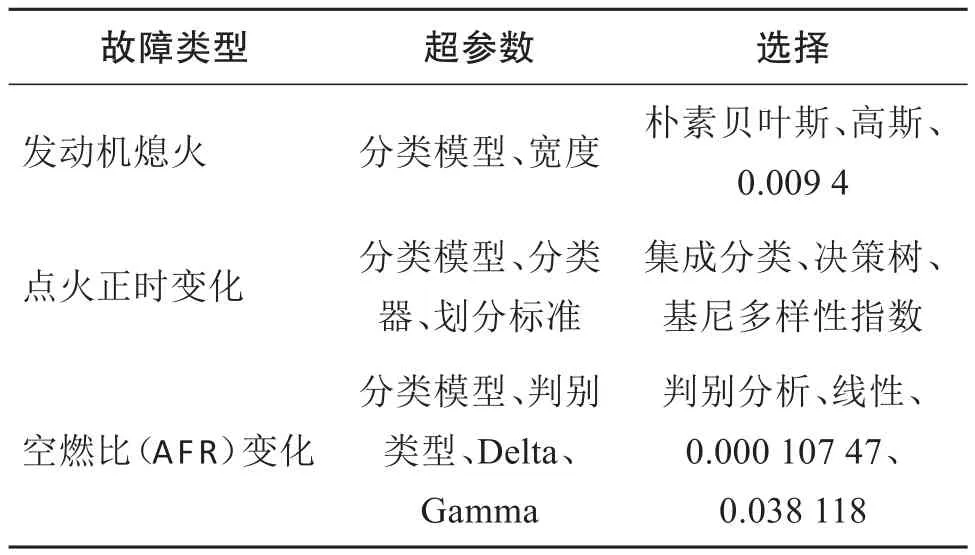
表5 模型2的最优模型参数选择

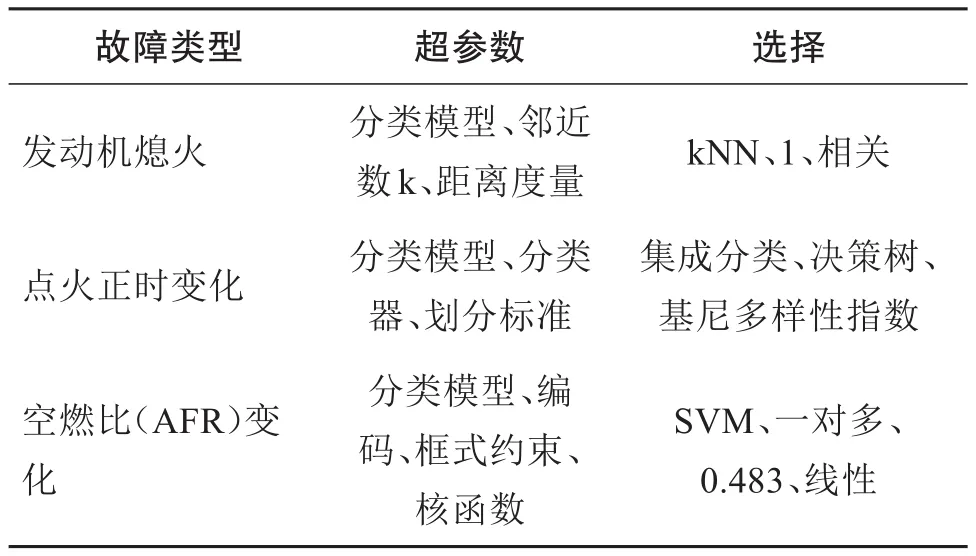
表6 模型2的最优模型参数选择

1.2.5 模型评价

将提取的特征矩阵输入图2的3个模型中，并使用表7中列出的指标评估每个模型的性能。TP是指被正确归类为故障数据的数据点，FP是指被错误归类为故障数据的数据点，TN是被正确归类为健康数据的数据点，FN是被错误归类为健康数据的数据点，特异性指的是健康被正确识别的比例，而精密度指的是故障被正确识别的比例。

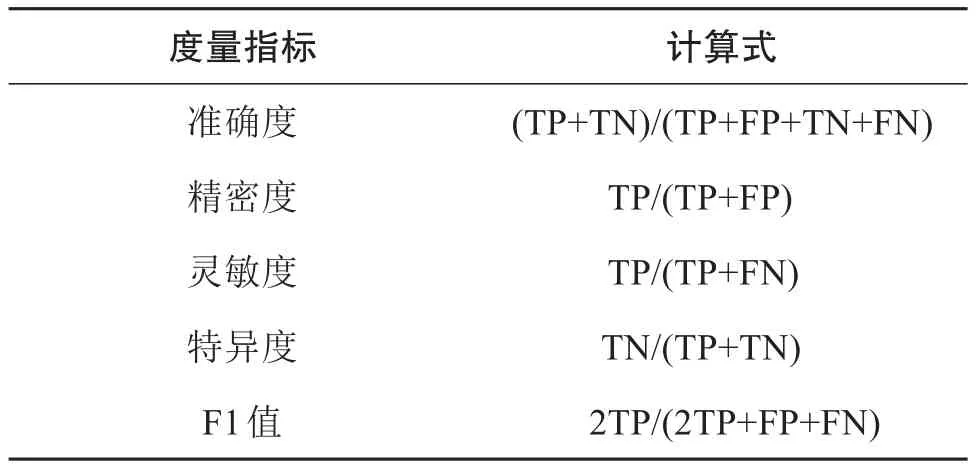
表7 模型度量指标

2 结果与分析

将总数据集以80∶20的比例划分为训练数据集和测试数据集。5倍交叉验证被应用于验证训练的模型。

2.1 3种模型的性能

对于3种故障试验情况，模型1的混淆矩阵如图3所示。由图3可以看出，在发动机熄火的情况下，模型1可以用于故障分类，其中FN和FP可以忽略不计，但对于点火正时变化和AFR变化数据，模型1由于操作复杂性较高，相对来说不太成功。

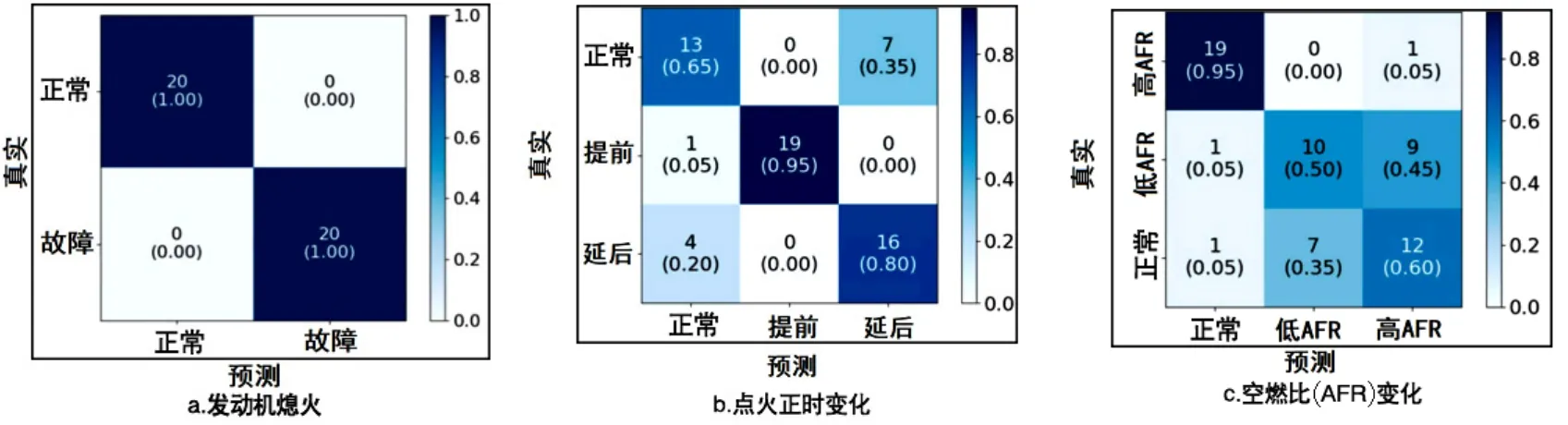
图3 3种故障数据的混淆矩阵——模型1

模型2的混淆矩阵如图4所示。从图4可以看出，FN、FP、TP、TN较模型1有明显改善。

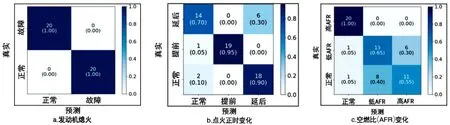
图4 3种故障数据的混淆矩阵——模型2

模型3的混淆矩阵如图5所示。与模型2相比，水平相近，虽然特征维数显著降低，但FN、FP、TP和TN与标准模型相比都有显著提高。

图5 3种故障数据的混淆矩阵——模型3

2.2 3种模型的评价

本研究的目的是在不同的故障条件下，以可接受的分类精度实时确定故障发动机信号。3种模型的评价指标结果如表8所示。

由表8可知，在3种故障条件下，使用贝叶斯优化模型比标准模型在准确性和F1分数上都有所提高。在发动机熄火情况下，由于这种故障情况简单，3种模型的评价指标都相同，对于其他2种更复杂的故障情况，与标准模型相比，模型2的准确度增加了5%，模型3的准确度增加了3%～4%。虽然模型3使用PCA显著降低了特征维数，但在同类型故障中，模型2和模型3的准确度和F1值的变化并不显著。

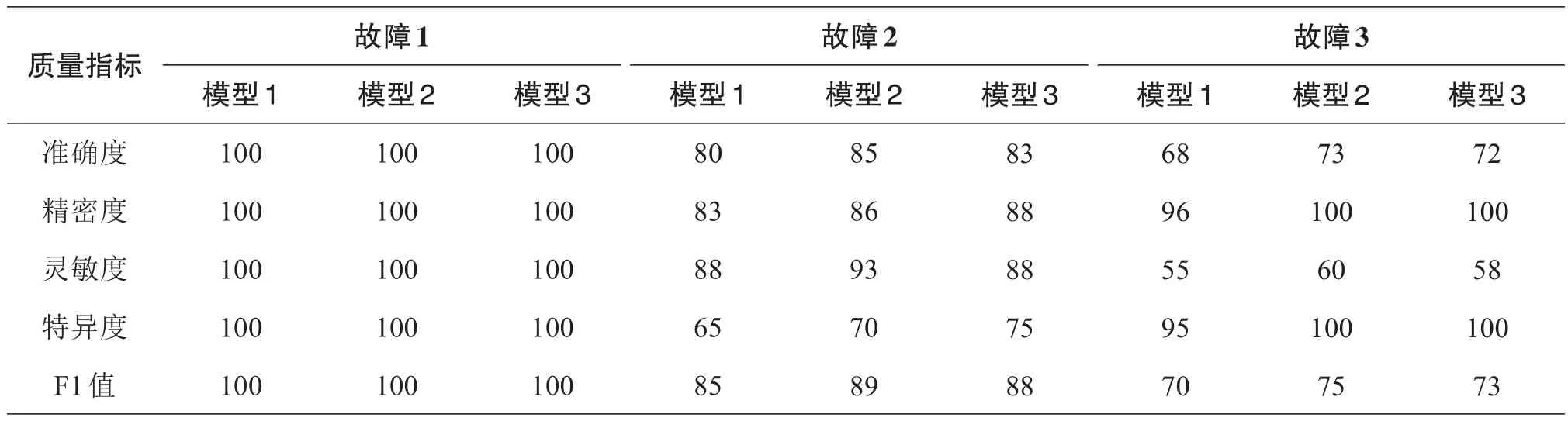
表8 模型评价指标的结果 %

模型2和模型3的总评估时间如图6所示，模型3的PCA降低了特征维数，使得评估时间比模型2显著降低了约20%。

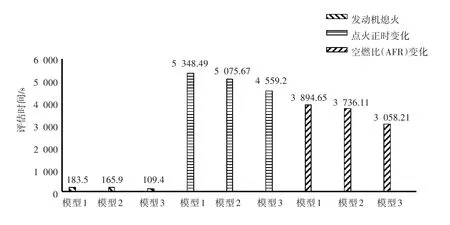
图6 3种故障下3种模型的评估时间

从图7中可以看出，与模型1和模型2相比，使用PCA的模型3的测试时间减少了8%～19%，这也是由于PCA对特征矩阵进行了降维。

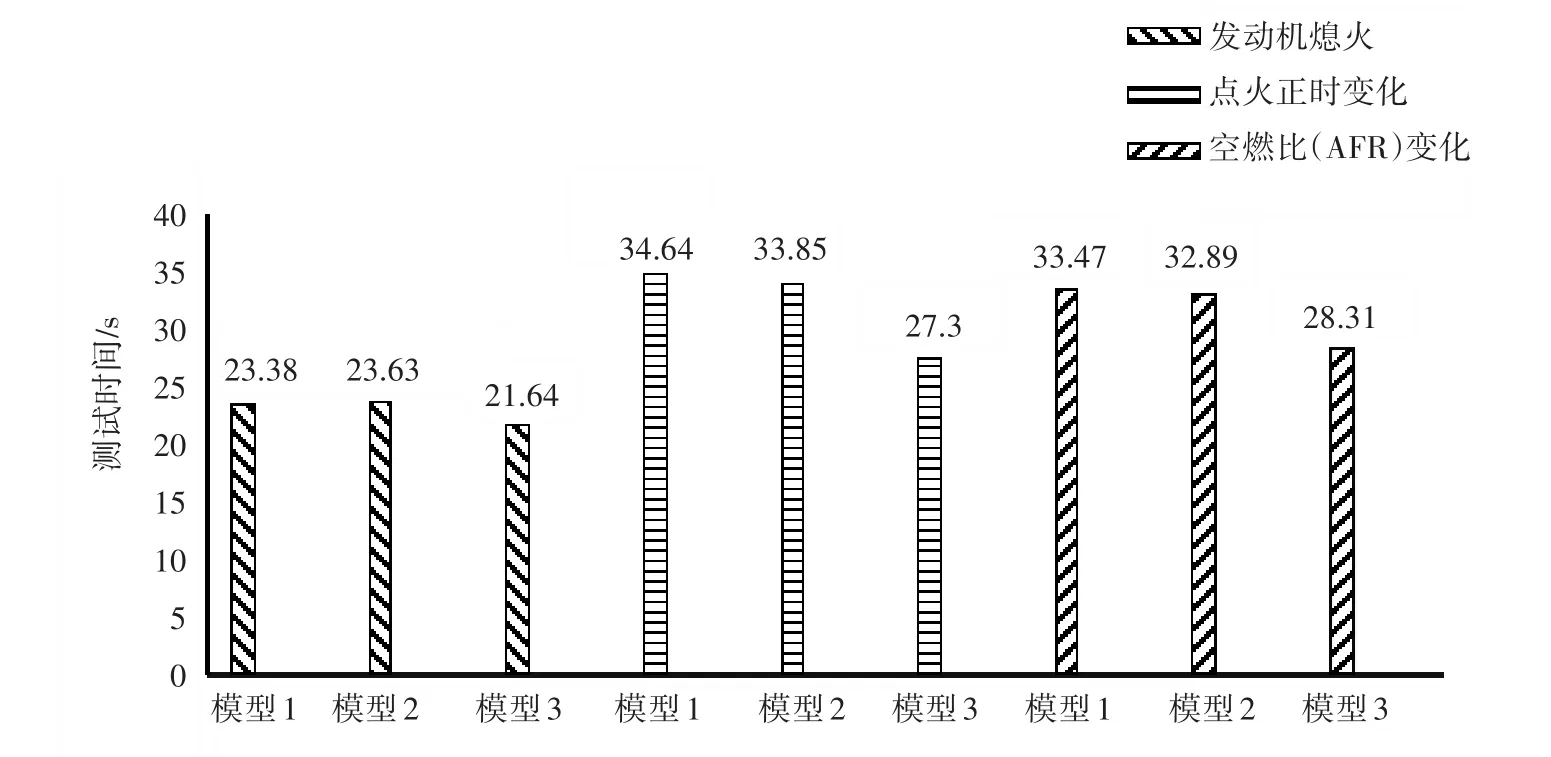
图7 3种故障下3种模型的测试时间

综上所述，基于贝叶斯优化模型的主成分分析方法是一种很有前途的、高效的方法，在不同的故障情况下，与标准模型相比，它具有更快的评估时间和更好的精度。

3 结论

本研究提出一种基于发动机声信号的分类方法，用于发动机故障诊断。采用发动机熄火、点火正时变化和AFR变化3种故障工况对该方法的适用性进行了训练和测试。分析和比较了3种分类模型：标准分类模型、贝叶斯优化模型和PCA结合贝叶斯优化模型。在这3种故障情况下，使用WPT分解声信号，并从小波系数中提取统计特征，然后将其作为3种模型的输入。研究目的不仅是为了达到更高的精度，而且还通过消除冗余特征来减少计算时间。所以，降维特征集将更适合于未来实时发动机故障诊断的在线实现。在3种故障情况下，相比标准模型，贝叶斯优化模型和PCA结合贝叶斯优化模型在准确度、精密度、灵敏度、特异度和F1值这5种评价指标上都有更优的性能。在与贝叶斯优化模型相似的准确度水平下，PCA结合贝叶斯优化模型的总评估时间比贝叶斯优化模型少约20%，测试时间少8%～19%。这表明，结合主成分分析和贝叶斯优化技术的WPT在发动机声故障实时诊断中具有广阔的应用前景。

在实际应用中，需要权衡故障分类精度与处理时间，这取决于工业应用及其具体需求。如果在故障诊断方面要求较高的准确性，并且有较多的处理时间，可能会选择贝叶斯优化模型；如果需要在短时间内识别一些故障，那么可以考虑PCA结合贝叶斯优化模型。