基于零部件编码和Hausdorff距离的装配体检索技术研究

张 鵾

（铜陵学院机械工程学院, 安徽 铜陵 244061）

0 引言

随着工业领域中CAD技术的广泛应用，各企业积累了大量产品的三维CAD模型。提高现有产品的三维CAD模型复用能力，对加快产品生产周期、提高产品市场适应力和提升企业竞争力有重要意义［1］。CAD模型检索技术主要分为零件模型检索和装配体模型检索。相较于零件模型检索，装配体模型检索技术能够实现产品级的模型复用，丰富了复用的内涵，得到了学界更多的关注。

装配体模型检索技术可分为基于拓扑结构和基于几何形状的方法［2］。在基于拓扑结构的方法中，通过构建装配体图或树的数据模型，将装配体的检索转换为图或树的匹配。周炜等［3］提取装配体模型中零件之间接触面信息，并对零件接触面数量、零件接触面关系进行编码，构建相似度矩阵，通过最优匹配得到装配体模型相似度。陶松桥等［4］通过运用复杂网络原理对装配体进行分析，建立了基于装配关系的相似度矩阵，对其邻居节点进行装配关系的计算和匹配，从而完成相似性度量。这2种方法都是通过分析装配体中零件间连接关系度量装配体的相似性，缺少对零件的相似性判断。基于几何形状的装配体检索技术一般使用直方图描述装配零件形状分布信息，利用推土机距离［5-6］（Earth Mover’s Distance， EMD）或改进的豪斯多夫距离［7］（Modified Hausdorff Distance， MHD）算法计算分布图的相似度。此外，Hu等［8］使用向量空间模型建立了针对轻量级装配体的检索方法。与基于拓扑的方法相反，基于几何形状的方法缺少对装配体中零部件连接关系的描述，构成的装配体模型知识仍显不足。

基于上述方法不能全面表征装配体信息的缺点，张杰等［9］提出了一种基于结构离散的方法，将装配体模型信息量化并融入描述符中，最终实现相似性度量。左咪等［10］首先对装配体模型进行信息的转化表达并归类，形成装配体类码连接图，再基于Weisfeiler-Lehman图核算法，对装配体类码图进行相似度计算，实现装配体间的分析比较。但上述方法的计算过程较为繁杂，对使用者有一定的技术要求。因此，针对装配体搜索技术，主要针对以下2个问题进行研究：（1）装配体信息尚未充分应用，不能同时有效地使用装配体的隐式信息、零部件属性及其关联关系；（2）计算复杂度较高，主要原因是使用算法较为复杂。

为解决上述2个问题，本文提出一种应用编码技术和Hausdorff距离的装配体相似度检索模型，并给出实例验证。首先，基于零部件的数字编码技术，在编码过程中融入装配连接信息，将装配体表示为由其零部件数字码构成的向量空间点集，再利用改进的Hausdorff距离算法计算点集之间的距离，以点集的距离表征装配体间的相似度。最后以实例验证了方法的有效性并进行了总结与展望。

1 装配体零部件的数字编码

1.1 零部件编码方案

建立完善的装配体零部件编码规则与系统，有利于实现零部件的检索，加快零部件的复用效率［11-13］。区别于零件的编码，装配体中零部件的编码一方面需要突出零部件特征，但另一方面不需要对零件特征进行详尽的描述。本文基于成组技术，借鉴万佳佳［14］、郑建鑫［15］、Deshmukh 等［16］的装配体分类编码思想，保留简洁有效的装配体零部件信息，使用通用性较好的数字码对零部件进行编码。

为避免装配体的编码过长且冗余，在编码过程中，针对部分不宜拆分为单个零件的部件，如溢流阀等液压元件或链条一类成型组件，本文将其视为广义上的一个零件进行编码。零部件编码码位示意表如表1所示。

表1 零部件编码码位示意表

表1中，零部件编码主要由零部件种类信息、几何信息、结构信息及预留码位4大区分块构成，每个区分块向下有各自细分类别，共有9个码位。表中括号内数字表示不同信息的不同数字码或范围。在编码规则中，既考虑了零部件信息又考虑了零部件间连接关系，并且预留拓展码位以便针对不同需求的进一步特征细化。

零部件种类由标准类、组件类、功能类3个码位构成，主要用来表示零部件的来源、分类和功能。其中，对于标准件的定义可以由国标扩展至企标，有利于零部件的归类。由于本文中针对的是广义零件，因此需要码位Ⅱ以区分零部件的组成。零部件的功能主要有连接与传动，由功能类码位Ⅲ体现。

在零部件的几何信息中，主要表征零部件的整体特征，包括零部件的形成方法、外形形状特征、整体形状尺寸。零部件的形成方法有回转形成或非回转形成。外形形状特征的纵向编码如表2所示，列出了9种常见的外形形状，其他未列项归于其他类中。对于回转体的形状尺寸，记录回转体最大直径φ和最高高度h，其形状尺寸比值r=h/φ；对于非回转体，其尺寸比值为该零部件最长尺寸lmax除以最短尺寸lmin，即r=lmax/lmin。零部件所有尺寸均在笛卡尔坐标系下进行测量。当零部件外形不规则时，则根据零部件的最小包围盒形状为回转或非回转体进行处理。尺寸的比值结果四舍五入取整，超过9的数值统一记为9。

表2 形状类别编码表

在结构信息中，编码表征了该零部件与其他零部件间的连接数量与连接类型。其中，需要注意的是，连接数量的多少决定了码位Ⅷ的位数数量，码位Ⅷ的编码按数字从小到大排列。表3对部分常见连接类型进行了编码。

表3 零部件连接关系编码表

1.2 零部件编码实例

为有效说明编码的实际过程，以某一顶杆凸轮机构为例进行编码。图1表示的是该凸轮结构，表4是该凸轮的相关参数。

表4 顶杆凸轮零件参数

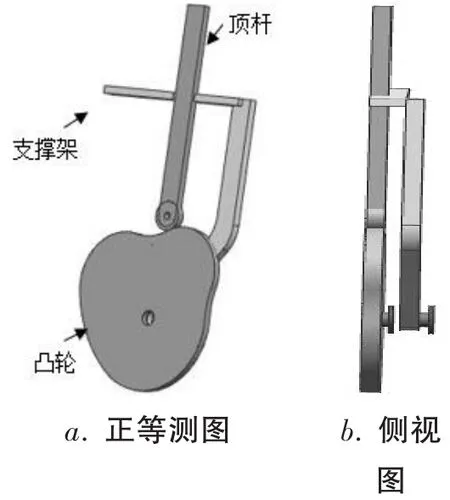
图1 顶杆凸轮机构

根据凸轮结构及参数，上述顶杆凸轮数字码空间集合为G1=｛101139288，100169218，101069248｝，编码说明如表5所示。

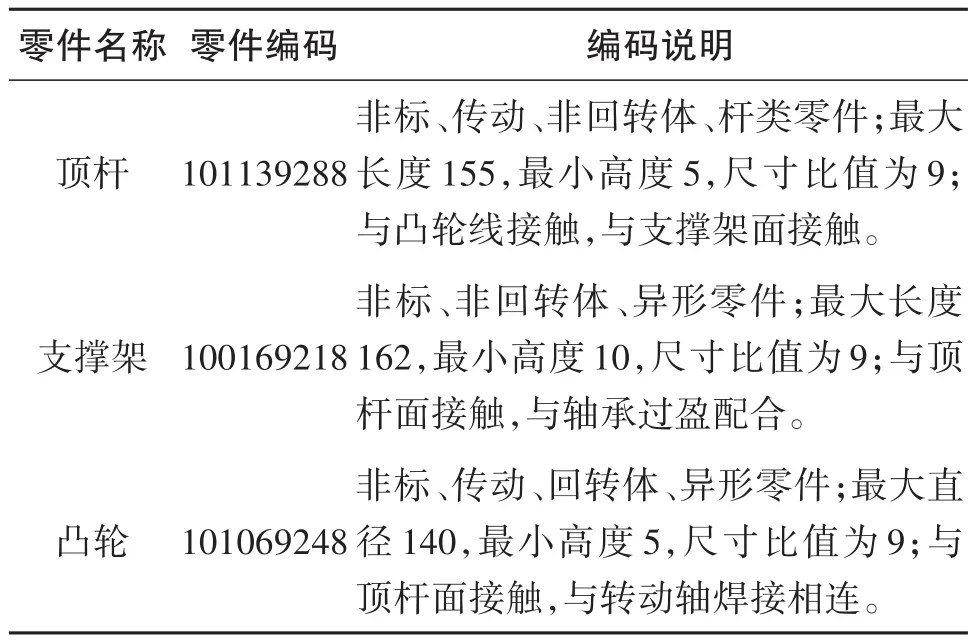
表5 顶杆凸轮的编码

2 基于Hausdorff距离的装配体检索

2.1 Hausdorff距离

Hausdorff距离［17］（Hausdorff Distance， HD）通常用于测量空间中子集之间的距离，它将存在于空间中的非空子集本身作为度量基准。在比较任意2点集间的相似性时，可以有效地处理多个点集的信息，并且不需要在点集之间建立一一对应关系。分别有 2 组非空集合A=｛a1，a2，…，an｝和B=｛b1，b2，…，bm｝，则A和B之间的Hausdorff距离定义为：

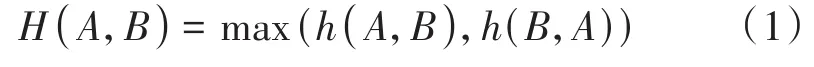
其中，

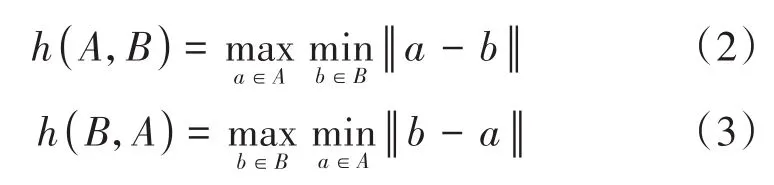
||·||表示点集A和B中各元素之间的距离范式，如欧氏距离等。由定义知，H（A，B）表征的是2个点集间最远的距离，称为双向Hausdorff距离，其是Hausdorff距离的基本形式。h（A，B）和h（B，A）则分别表示的是点集A到B以及点集B到A的单向Hausdorff距离。

本文中，为抵消数字码数值在定义时的随机排序影响，改进Hausdorff距离定义中的距离范式为子集元素的欧氏距离与元素中极大值的比值。同时，考虑到零部件不同特征的重要性，可自定义给予不同码位不同的权重。在计算过程中，由于Hausdorff距离度量的是2点集中最远距离，这种比较方法会极大影响度量结果，如装配体A与B其99%占比的零部件完全一致，仅有1%的零部件完全不同，依据Hausdorff距离判定方法，则A与B的相似度较低因其未考虑其99%的零部件相似。因此，本文采用与Zhang等［7］一致的方法将平均距离作为度量距离，降低了比较结果对离群点的敏感性。改进后的双向Hausdorff距离定义不变，单向Hausdorff距离定义如下：

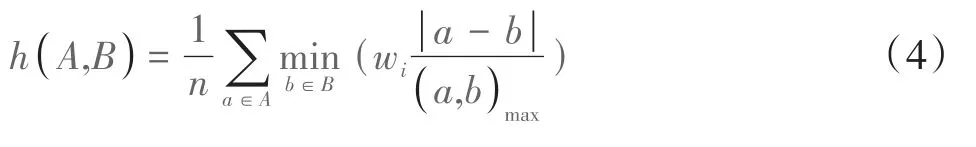
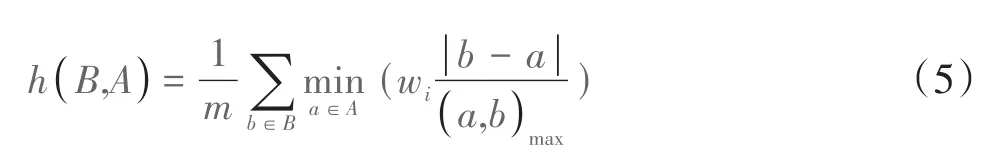
式（4）和式（5）中，n、m表示装配体A、B的零部件数量，wi指的是不同码位的权重值，满足：

当n≠m时，单向Hausdorff距离不一致，对于双向Hausdorff距离无影响。为保持一致性，本文使用的是双向Hausdorff距离。

2.2 装配体相似性计算

装配体相似性计算的整个过程是将装配体数字化编码为一个点集，并使用改进的Hausdorff距离来解决模型检索问题。其基本步骤包括：

1）借助数字编码方法将装配体转换为多维空间的点集；

2）使用建立的点集构造装配体模型的空间集合；

3）通过改进的Hausdorff距离计算点集之间的相似性。

在搜索过程中，输入要检索的装配体模型空间集合后，搜索者可以获得按相似性降序排列的结果。以检索装配体A与B、C间的相似度为例，其检索过程如表6所示。

表6 装配体检索过程

3 实例验证

为说明本方法的具体运算过程并验证方法的有效性，本文利用顶杆凸轮与摆杆凸轮、曲柄滑块机构进行相似度实例计算验证。

在验证前，考虑到顶杆凸轮与摆杆凸轮同属凸轮机构，因此初步判断二者的相似度较顶杆凸轮与曲柄滑块机构间的相似度更高，即二者的距离更小。构成顶杆凸轮机构的向量空间为｛101139288，100169218，101069248｝。摆杆凸轮和曲柄滑块机构的零部件名称及编码等信息如图2所示。摆杆凸轮和曲柄滑块机构的向量空间分别为｛101139218，100139218，101069248｝和｛10216511，101139211，101139211，10116310｝。

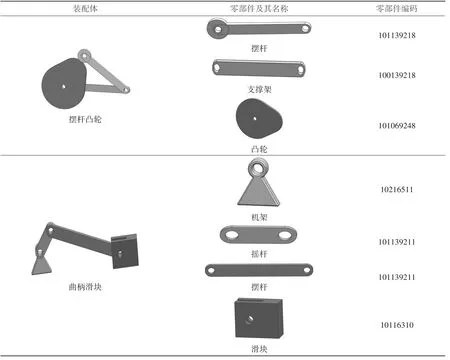
图2 检索装配体实例

根据上述3个装配体编码，分别计算顶杆凸轮与摆杆凸轮、曲柄滑块机构的相似度。由于几何信息及结构信息更能凸显零部件特征，本文定义零部件种类信息、几何信息、结构信息的权重分别为30%、35%和35%，其中，形状类别码位和接触方式码位权值为0.15，度的权值为0.2，其他码位均为0.1。

使用改进后的Hausdorff距离计算，得出顶杆凸轮与摆杆凸轮、曲柄滑块机构的距离分别为0.025和0.099，即顶杆凸轮与摆杆凸轮的Hausdorff距离较其与曲柄滑块机构的Hausdorff距离更近，基于距离越近相似度越高的原则，顶杆凸轮与摆杆凸轮的结构相似度更高，方法有效。

4 结论与讨论

通过数字编码方法构建装配体的向量空间，将装配体模型数字化为数字集合，同时，借助改进的Hausdorff距离方法计算数字集合间的距离，从而将装配体间的相似性检索问题转化为一维的集合计算问题。最后通过3个装配体模型的实例分析，验证了方法的有效性。

相较于其他相关算法，基于零部件编码和Hausdorff距离的装配体检索过程优势在于其使用的Hausdorff距离，其计算是在一维集合中进行，速度较快；且在编码的同时考虑了装配体几何与结构信息，以及这些信息在装配体特征中的权重占比，对装配体的信息及特点表征相对全面。但计算之前需要对装配体零部件及关联关系进行分析、提取和编码，方法的预操作阶段较为冗杂。

基于上述问题，在后续研究中，提高编码过程的便捷性以及对码位特征权值的优化定义是进一步改进的重点。