基于虚拟流场与MSD模型的道路拥堵缓解算法
2023-01-16陈云飞冀杰柏鉴张宇航赵颖
陈云飞, 冀杰, 柏鉴, 张宇航, 赵颖
西南大学 工程技术学院,重庆 400715
借助快速发展的车联网通信技术,智能网联车辆能够通过智能交通设施或其他车辆及时地获取交通信息,并用于提高道路通行效率,这已经成为智能交通领域的重要研究方向之一.当传统道路出现瓶颈路段时,车辆必须在所在车道消失前及时进行换道,但传统道路的车辆与其他车道上的车辆因缺乏信息交互和合作,容易造成没有足够的安全间距完成车道变换,进而导致车辆速度降低,形成交通拥堵并导致该路段的车辆通行效率降低[1-2].为了解决这些拥堵问题,现有的算法分为两类: 基于数据驱动[3]和基于模型控制[4]的算法.基于数据驱动的算法依托强化学习等方法可以在无法精确建立模型的时候对道路交通进行有效控制,如郝建根[5]将数据驱动的方法应用于交通控制中,并通过仿真结果验证该算法可以有效缓解交通拥堵,提升交通效率.然而基于数据驱动的方法需要大量的数据进行学习训练,因此基于模型通过对单个车辆或车队进行建模并利用转联网技术控制车辆行驶轨迹进而缓解交通拥堵的研究依然是当前的热点[6-8].同时,由于交通瓶颈路段上游的车辆换道行为较为复杂[9],在快速路环境下通过协同换道的方法解决瓶颈路段的拥堵问题还有待进一步研究.
为了减少车辆的通行时间,许多文献基于车—车通信的方式对智能网联汽车的换道行为控制进行研究[10-12].张荣辉等[13]基于多车协同驾驶控制结构,提出了一种无人驾驶车辆换道汇入的驾驶模型及策略,并基于高阶多项式方法,结合舒适性等指标得到车辆换道的运动轨迹; Ding等[14]提出了一种基于规则的调整算法,通过对先进先出的换道规则进行优化,以最小的计算能力实现车辆通过匝道路口的近最优合并序列; Stern等[15]指出避免瓶颈路段车辆的频繁加速和刹车可以有效减少车辆的通行时间; Ntousakis等[16]采用了双层控制器确保每辆车都能在没有任何拥堵干扰的情况下顺利地通过瓶颈; Phan等[17]开发了该算法的上层控制器,通过优化每条道路的车道使用情况和自动驾驶车辆的位置,显著提高了交叉路口的通行效率.
鉴于智能网联技术的快速发展,一些学者开始试图通过车—车/车—路互联的方式增加车辆速度、 降低行车间距,从而进一步提升瓶颈路段的通行效率.Han等[18]提出了可变释速控制法(Variable Speed Release,VSR),通过提高车辆速度,增加缓冲车头时距,从而提高整个道路系统的车辆通行数量并降低交通拥堵的发生概率.Phan等[19]提出了一种协同式空间分配法,基于车辆纵向横向约束关系,控制车辆加速达到最大速度,使其主动产生安全间隙,最终使换道车辆以最大速度和最小间隙快速通过瓶颈,达到提升瓶颈路段的交通通行能力的目的.
许多学者受到自然界的启发,发现交通流与自然流体存在很多的相似点,并对其进行了大量研究.如Light等[20]将交通流比作流体,建立了车流的连续性方程,提出了车流波动理论.在自动驾驶技术不断发展的背景下,人们开始将流体的特性运用到自动驾驶的运动控制中,如依照流水避石的原理规划出自动驾驶车辆的避撞路径[21].Cheng等[22]提出了在两平行板之间或圆柱体周围的虚拟黏性流体流动模型,基于该模型可以实现车辆车道保持和避免碰撞的双重功能.除此之外,研究人员发现由质量—弹簧—阻尼器(Mass-Spring-Damper,MSD)构成的物理模型具有天然的稳定性并将其用于换道之后的车辆队列控制中[23-25].Bang等[26]将MSD模型用于换道汇入控制中,通过控制弹簧刚度和阻尼系数达到降低车辆汇入行为对行驶过程产生的影响.
本文受到自然界中流体加速通过瓶颈的现象启发,建立了瓶颈路段的流体理论模型,从而获得了车辆的速度及换道信息.同时,为了保证车辆换道过程的安全性,引入了虚拟弹簧阻尼模型对参与协同换道的车辆进行运动控制.根据以上两点,本文提出了一种基于虚拟流场和质量—弹簧—阻尼模型(Virtual Flow Field-Mass Spring Damper,VFF-MSD)的瓶颈路口拥堵缓解控制算法,能有效降低车辆通过瓶颈路段的通行时间.具体来说,车辆进入瓶颈路段的虚拟流场后,跟踪该路段流场的纵向速度并加速通过瓶颈,同时,在流场横向速度最大时开始以最大横向速度进行换道.另外,车辆在换道时向目标车道进行投影,并建立投影车辆与前车和后车之间的虚拟MSD模型,借助弹簧与阻尼的虚拟作用力保持车与车之间的安全距离,防止车辆在换道过程中发生碰撞.
1 基于虚拟流场的车辆换道策略
在实际道路环境中,施工维护、 车辆故障或车道合并都会形成瓶颈道路场景,而流体在经过类似瓶颈时,会加速流过瓶颈而不会形成堵塞.受该自然现象启发,建立如图1所示的瓶颈道路的虚拟流场,使车辆能够跟踪流场中流体的纵向速度并找到合适的横向位置进行换道.
建立准确可靠的虚拟道路流场模型是实现车辆换道策略的前提,图1上部和中部分别为3车道道路瓶颈路段的简化模型及虚拟流场.将整个道路表面视为流场,以x方向为道路的纵向方向,y方向为垂直于x方向并建立坐标系.假设流体从道路左侧流入,右侧流出,其余边界为静止的无滑移的墙壁.为了使道路上车辆的加速度曲线更加平滑,防止由于瓶颈处车道数量的突然变化而导致车辆速度突变,同时,为了合理利用现有道路空间,将车辆的换道初始位置适当提前,在瓶颈路段前建立虚拟流场边界.

图1 基于虚拟流场的车辆换道策略
根据计算流体力学的基础理论,流体运动的无穷小微团的连续性方程的偏微分方程形式为

(1)
式中,ρ为流体密度,V表示质点的速度矢量.
由于该路段中行驶的车辆数量不变,所以设置流体在入口和出口的质量与流量相同,且流体为不可压缩流体,即密度ρ恒定.并且本文只考虑道路平面上的车辆运动情况,不需要考虑道路竖直方向上的运动情况,因此流体的连续性方程可表示为

(2)
式中,u,v分别为流体速度在x方向和y方向上的分量.
根据流体的动量方程,可得到该条件下x方向上流体的纳维—斯托克斯方程的守恒形式:
(3)
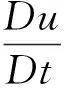
将公式(2)带入到公式(3)中可得:
(4)
同理,可得y方向上流体的守恒方程为
(5)
虚拟流场条件下不需要考虑外界作用力和温度的变化,因此,道路虚拟流场的微分方程最终表示为
(6)
(7)
在Ansys Fluent软件中,采用层流模型和压力耦合的半隐式算法(SIMPLE)对建立的虚拟流场模型进行计算.根据公式(6)和公式(7)获得流场中每个节点的状态,并对车道1、 车道2和车道3中线上的速度信息进行采样,用来表示该车道上车辆的速度信息.由于车道1为消失车道,因此,采用从车道1起始位置中点出发的流线代替车道1的中线,对这些采样点数据进行拟合,获得车道上纵向和横向速度随纵向位移的变化曲线,如图1下部所示.
图1中的蓝色曲线分别代表车道1和车道2流场的横向速度随纵向距离的变化情况,其中,vylane1与vylane2分别表示采用Fluent软件分析出的流体在车道1和车道2达到的最大横向速度,其对应的xlc1和xlc2分别代表流场内车道1和车道2横向速度最大时的纵向位置.由于在流场中各车道纵向速度差别很小,所以不作区分,用红色曲线表示整个流场的纵向速度随纵向位移的变化情况,该曲线可被看作是车道上车辆的目标纵向速度.xstart,xacc,xms,xend分别表示瓶颈路段开始位置、 车辆加速开始位置、 车辆纵向速度达到最大的位置以及瓶颈路段结束位置.当车道1和车道2上的车辆行驶到该位置且符合其他换道条件时,车辆开始执行换道命令.为了减少计算量,各车道满足换道条件的车辆均以流场内的最大横向速度进行横向匀速换道,由于车道1会在瓶颈处消失,所以车道1上的所有车辆必须改变车道进入车道2.同时,为了最大化利用道路空间,避免因各车道车辆分布不均造成拥堵,当车道3上的车辆数量小于车道2的车辆数量时,需要使车道2上的车辆逐渐换道进入车道3,换道条件框架图如图2所示.

图2 各车道换道条件框架
2 基于虚拟MSD模型的车辆控制
2.1 虚拟MSD模型建立
通过对流体的分析与模拟,获得了车辆在通过瓶颈路段时的加速过程和换道策略.同时,车辆在行驶过程中还需考虑交通系统的安全性,因此,需要对车辆的纵向运动和横向运动轨迹进行分析,在多车辆交通环境中,为了方便计算和分析,对车辆的纵向运动及横向运动进行简化,如公式(8)-(11)所示:
(8)
(9)
(10)
yi(t)=vyi(t)×t
(11)
式中,xi(t)表示车辆i在x方向上的位移,vix(t)表示车辆i在x方向上的速度,aix(t)表示车辆i在x方向上的加速度,ji表示车辆i在x方向上的加速度变化率,yi(t)表示车辆i在y方向上的位移,vyi(t)表示车辆i在y方向上的速度.

图3 车辆虚拟MSD模型
对于纵向运动,本文采用MSD控制模型,即将本车与前车看作质量体并用虚拟的MSD模型连接起来,通过弹簧力和阻尼力使车辆保持安全车距并跟踪前车行驶.当车辆无前车时,车辆沿流场速度加速行驶通过瓶颈路段.当本车前方出现车辆时,如图3所示,在本车与前车间建立虚拟MSD模型,系统仅对本车产生作用力,对前车无影响,从而使车辆能够以安全距离跟踪前方车辆.理想安全距离SM,F表示该虚拟MSD模型的平衡状态,当MSD模型处于非平衡状态时,会控制本车运动恢复至平衡状态.
在t时刻,两车间的距离可以表示为
Δx=xF(t)-xM(t)-L
(12)
车辆间距误差为
δ=Δx-SM,F
(13)
其中,理想安全距离SM,F由恒定车头时距(Constant Time Headway,CTH)计算得:
SM,F=h·xM(t)+s0
(14)
所以在t时刻车间距离误差为
δx=xF(t)-xM(t)-L-h·xM(t)-s0
(15)
车辆速度误差为
(16)
根据图3所示的运动模型以及振动力学相关理论,假设被控车辆质量为m,车辆前进方向为正方向,同时设定模型仅对后车产生影响,对前车没有作用力.以车辆间距误差为弹簧控制对象,以车辆速度误差为阻尼控制对象建立模型的运动方程为
(17)

如图4,对于需要换道的车辆,首先在目标车道上投影一个与本车纵向轨迹相同的虚拟车辆(如图中红色虚线车辆),并与目标车道前、 后车辆建立虚拟MSD模型,此时目标车道前车为本车的前车,同时本车为目标车道后车的前车.在本车车道变换的横向位移过程中,通过虚拟MSD模型控制本车与后车运动,使本车与目标车道前车和后车形成安全车队,保证车辆换道时的安全.在表1中给出了所提出的VFF-MSD的伪代码.

表1 VFF-MSD伪代码

图4 虚拟MSD协同换道
2.2 弹簧刚度和阻尼参数确定
在车辆运动控制过程中,需要能够快速到达目标位置并尽量避免周期性振动.根据振动力学理论可知,临界阻尼模式下的物体能够以最快速度到达平衡位置并不会发生周期性的振动扰动,满足车辆控制要求,所以,在虚拟MSD模型中采用临界阻尼对车辆进行控制,即:
(18)
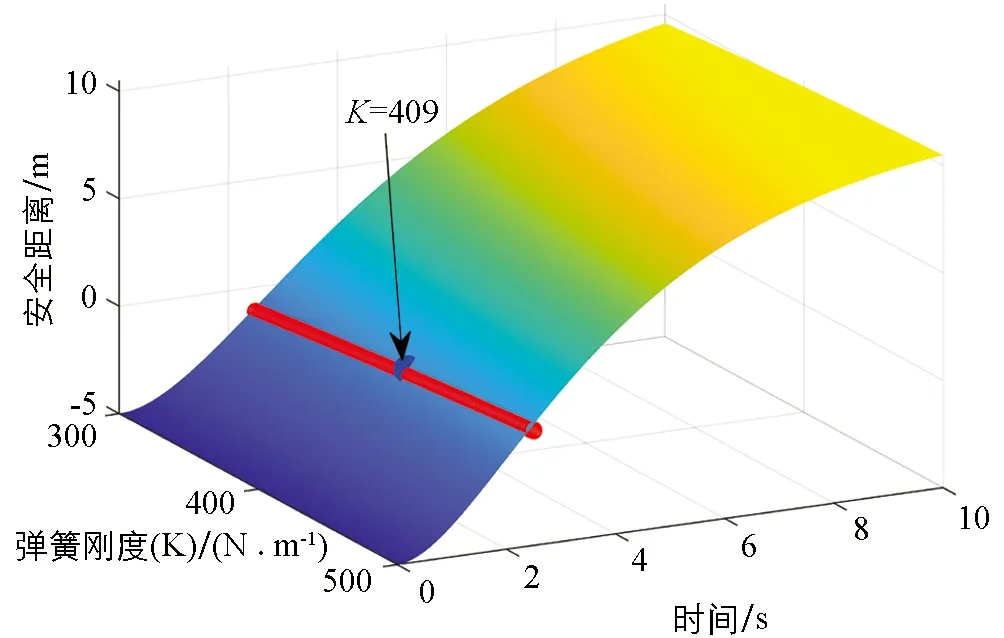
根据流体力学分析结果可知,车辆在换道过程中要对纵向运动和横向运动同时进行控制,为了保证车辆在换道过程中不与前后车发生碰撞,需要使车辆到达横向碰撞临界位置前,与前车的纵向距离大于安全距离.如图5所示,对车辆最小安全距离进行简化,不考虑在换道过程中车身的横摆角度偏移,约束条件为
Sf=xF(t)-xM(t)-L>0
(19)
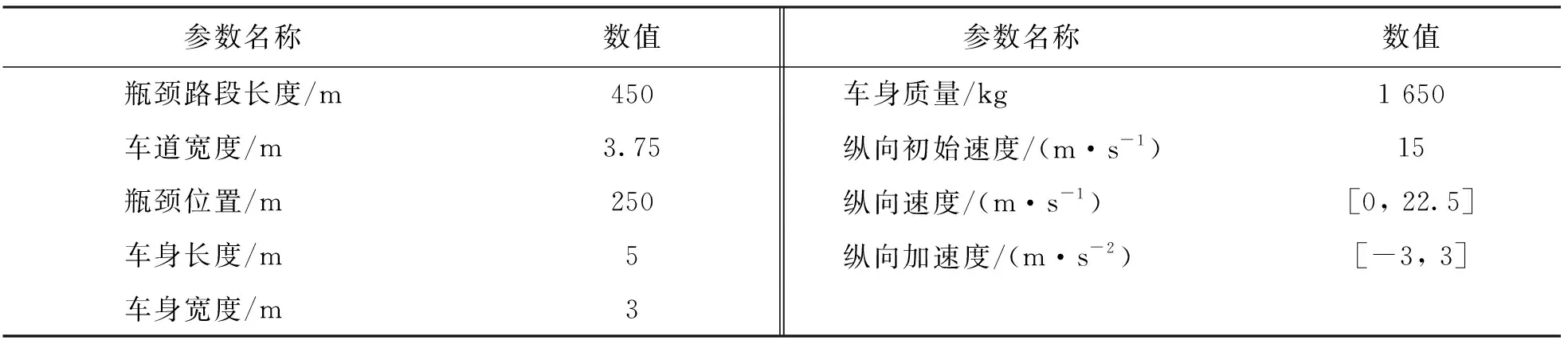
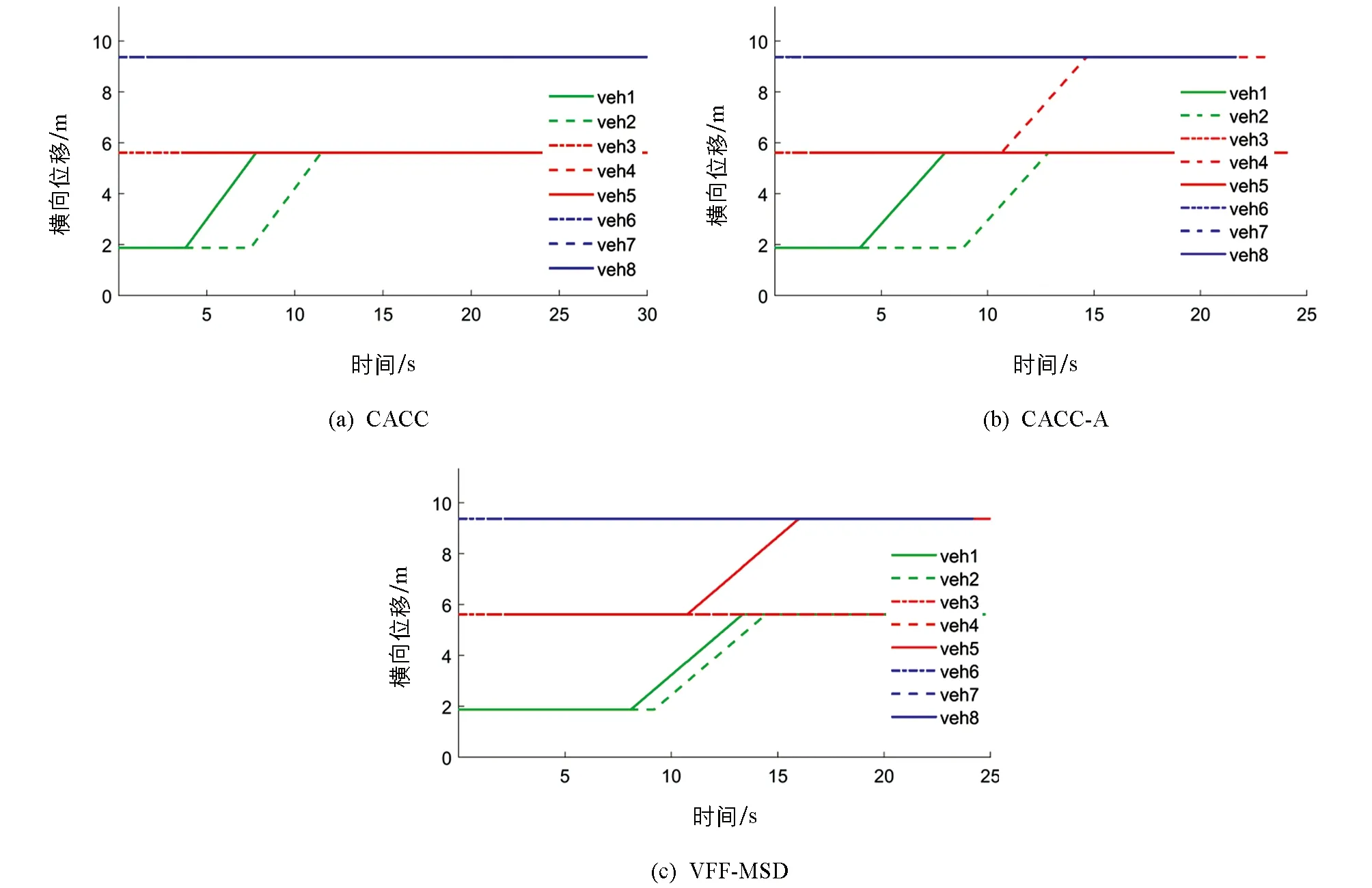
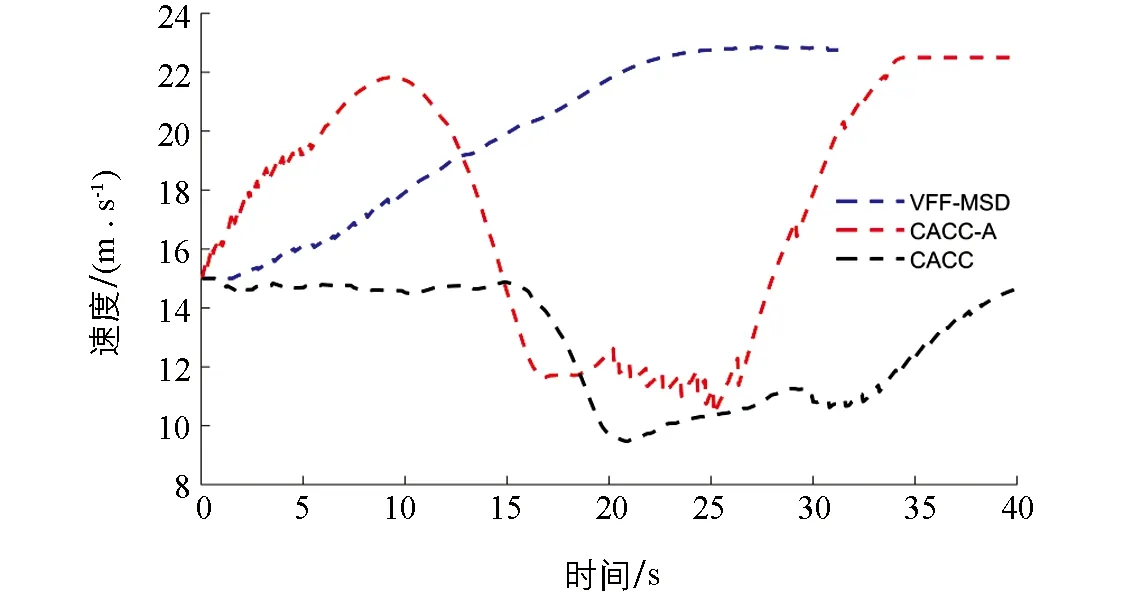
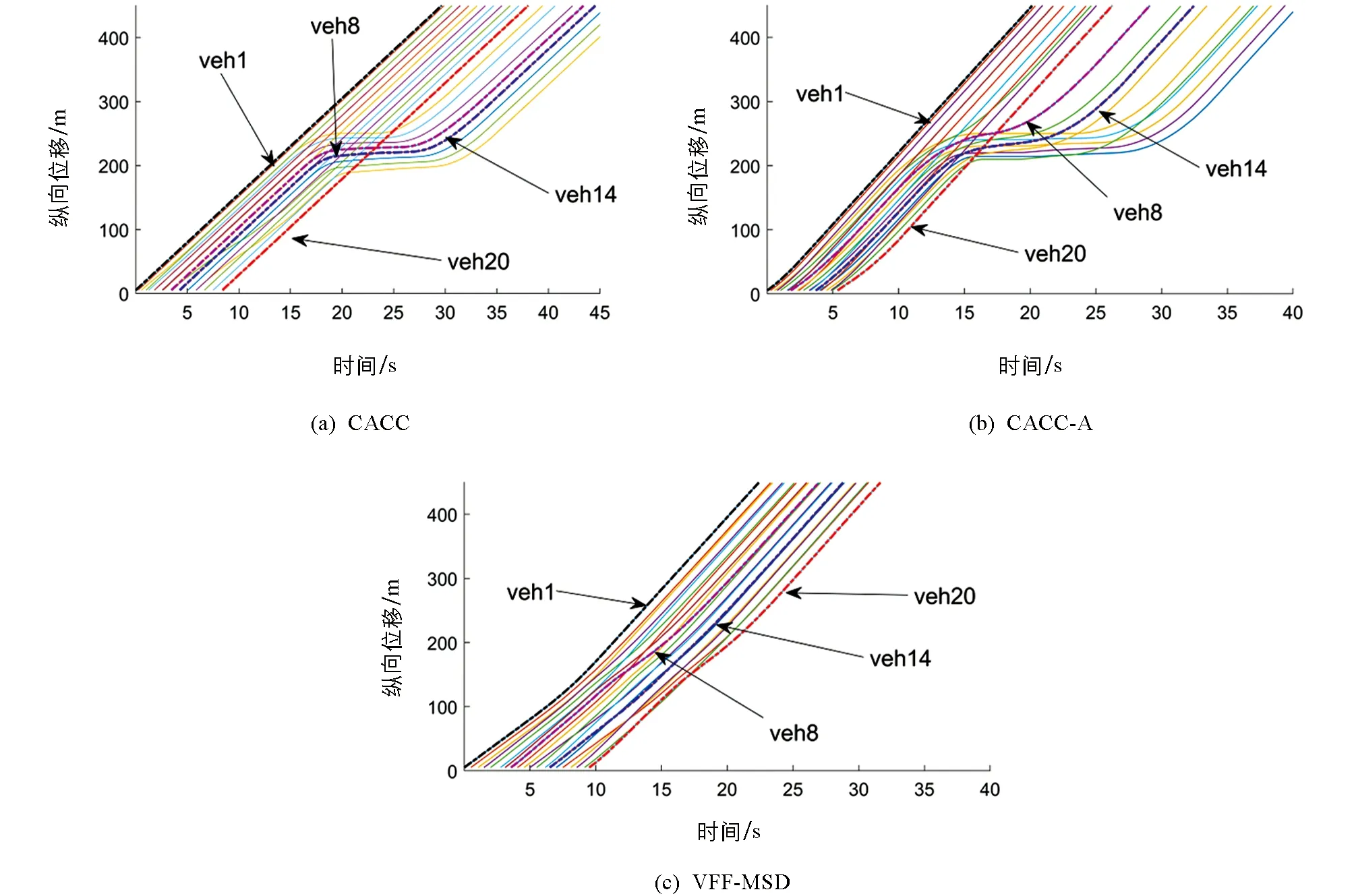
vy·t (20) 其中,d表示车道宽度,M表示车身宽度,vy表示车辆换道时的横向速度. 为了保证换道过程的平稳和舒适性,需要使车辆换道过程中的纵向加速度变化率尽可能最小. 图5 车辆换道临界安全距离 选取两车并列行驶的工况作为参数的确定工况,由于该工况下需要保证两辆车产生的位移差大于车身长度才能满足安全条件,是所有初始条件工况中需要产生的最大位移差,所以在该工况下确定出的参数值能满足其他工况的安全要求.将不同的K值与其对应的临界阻尼C值带入公式(17)中,并根据公式(19)-(20)的约束,可以得到车辆行驶过程中的车辆加速度变化率随时间t和弹簧刚度K的变化,如图6所示. 从图6可以看出,满足公式(18)的条件下,在相同时间范围内,车辆的加速度变化率随弹簧刚度K的增大而增大,因此,车辆加速度变化率最小可以转化为满足条件的最小弹簧刚度K,约束条件最终表示为 (21) 车辆之间的安全距离Sf随时间t与弹簧刚度K的变化如图7所示.从图7可以看出,随着弹簧刚度K与时间t的参数值增大,前后车之间的纵向距离Sf也随之不断增大.根据公式(20),可得到前后车辆横向距离为0时的临界时间,如图7红色曲线所示,根据公式(19)可得到在红色曲线上满足纵向距离Sf>0时的最小值K=409,其对应的临界阻尼C=1 643,即图7中蓝色点位置. 图6 加速度变化率随时间变化关系 图7 安全距离与弹簧刚度和时间的关系 通过SUMO交通仿真软件对所提出的VFF-MSD算法进行仿真测试,其内置的TraCI (Traffic Control Interface)功能可以对场景中车辆进行检索与控制.假设瓶颈路段的车道由3车道减少为2车道,车辆在进入瓶颈区域时在3个车道均匀分布,且车道1的所有车辆在到达瓶颈路口前必须改变车道.VFF-MSD算法的目标是通过控制自动驾驶车辆的纵向轨迹和横向轨迹,从而减少车辆通过瓶颈路段的平均时间,避免拥堵产生.车辆与瓶颈路段的参数如表2所示. 表2 瓶颈路段道路与车辆参数 为了验证算法在不同交通密度场景下的性能,分别建立了场景一(8辆车)与场景二(20辆车)对所提出的算法进行仿真分析,设定场景一中车道1的车辆与车道2、 车道3的车辆并排行驶,场景二中20辆车为随机输入. 通过瓶颈路段时所有车辆的平均速度(Vavr)、 平均行驶时间(Tavr)以及通行效率(Ef) 3个指标对算法性能进行对比.在不考虑碰撞等车辆安全约束的条件下,使车辆以最大加速度加速到最大速度并通过瓶颈路段,可以计算出车辆通过瓶颈路段的最小时间Tm,定义Ttol为所有车辆通过瓶颈路段的时间,则通行效率Ef可以定义为 (22) 为了与目前研究结果进行比较,保持道路与车辆参数不变,在场景中采用车辆加速(CACC-A)与不加速(CACC)条件下与所提出的VFF-MSD算法进行对比分析.该CACC算法采用恒定车头时距策略,在控制过程中与VFF-MSD根据是否存在领队车辆控制速度的策略类似,当车辆距离前车较远或无前车时,激活速度控制模式; 当车辆与前方车辆的间距较近时,激活间距控制模式,与前车保持固定车头时距进行行驶; 当车辆与前方车辆的间距更小时,激活间距接近控制模式,防止车辆发生碰撞等安全隐患.其加速度由前一时刻的速度和期望速度之差决定[28-30].换道模型可参考文献[31]. 在场景一中,假设车道1有两辆车veh1和veh2,车道2有3辆车veh3~veh5,车道3有veh6~veh8 3辆车,且3个车道的车辆并排行驶.如图8所示: 图8 场景一中8辆车初始位置 图9表示了3种算法下车辆速度随时间的变化情况,由于没有采用加速策略,图9(a)CACC算法速度被限制在15 m/s,且在换道时为了给车道1中车辆预留出足够的安全距离,车道2上veh3,veh4,veh5的速度都有明显下降以至低于初速度的情况.图9(b)CACC-A算法通过加速,速度情况有所改善,但可以看出其合作变道时频繁的加减速导致换道车辆的速度波动较大.图9(c)由于采用了流体的加速策略和MSD模型的跟踪策略,更符合自然条件的一般规律,VFF-MSD算法的速度曲线更加平滑,对于合作换道时的速度波动情况有极大的改善,受换道影响减速的车辆更少,整体速度呈加速趋势. 图9 场景一CACC,CACC-A,VFF-MSD算法车辆速度 图10和图11分别表示了场景一中3种算法的车辆纵向位移和横向位移随时间变化的关系.其中绿色的虚线和实线代表1车道的veh1和veh2,红色的虚线和实线分别表示2车道的veh3~veh5,蓝色虚线和实线分别表示3车道的veh6~veh8.在算法CACC中,车辆由车道1换道进入车道2中,由于速度受限,其通过瓶颈路段的时间更长.CACC-A算法中后方车辆的轨迹也存在一定程度的减速扰动.VFF-MSD算法在换道时机的选择上相比两种CACC算法更晚,在安全换道的前提下更充分利用了道路的空间,有利于拥堵的缓解,且可以看出车辆整个行驶过程的轨迹扰动程度较小. 图10 场景一CACC,CACC-A,VFF-MSD算法车辆纵向位移 图11 场景一CACC,CACC-A,VFF-MSD算法车辆横向位移 3种算法的结果如表3所示,采用了加速策略后,CACC-A与VFF-MSD的车辆平均通行时间分别为21.68 s和23.71 s,平均速度分别为21.11 m/s和19.63 m/s,均优于不采用加速策略的31.16 s和14.84 m/s,表明采用加速方式可以有效地提高道路瓶颈路口的通行速度和降低通行时间. 由于CACC-A的加速策略选择在更早的时间以最大加速度进行加速,所以在车辆较少的场景下,其各项性能均优于本文提出的VFF-MSD算法,但也因此导致车辆在换道的过程中需要更大的减速来提供换道所需的安全距离,频繁的加减速不利于乘客的舒适性,同时也不利于减少能量损耗. 表3 场景一中3种算法的性能结果 场景二中,20辆车随机进入道路模拟场景中,且数量在3个车道上均匀分布.由于场景二中20辆车的速度图比较复杂,采用所有车辆的平均速度代替.3种算法的平均速度随时间的变化关系如图12所示,其中蓝色虚线代表VFF-MSD算法,红色虚线代表CACC算法,黑色虚线代表CACC-A算法. 图12 场景二CACC,CACC-A,VFF-MSD算法平均速度 通过平均速度可以看出CACC-A选择加速的时机更早且加速度更快,但在到达瓶颈附近时和CACC一样都会产生明显的速度下降,通过瓶颈后,速度开始上升到期望速度,而VFF-MSD的平均速度一直呈上升趋势,没有明显速度降低,通过瓶颈所需的时间更短,证明所提出的VFF-MSD算法可以使车辆快速通过瓶颈路段. 图13和图14分别表示了场景二中车辆在3种算法下的横向位移和纵向位移随时间的变化情况,黑色线表示的veh1和红色线表示的veh20分别代表进入该场景的第一辆车和最后一辆车.绿色线表示的veh8和蓝色线表示的veh14为场景中随机选择的两辆车.CACC和CACC-A算法都出现了明显的拥堵现象,veh8和veh14都有不同程度的减速情况出现,而VFF-MSD算法在通过瓶颈路段时表现良好,车辆没有明显的减速和停止情况,对拥堵有明显的改善,且可以明显看出所有车辆通过瓶颈路段所花的时间更短. 在场景二中VFF-MSD的3项参数都明显优于另外两种算法,这是因为当场景中车辆较多时,CACC和采取最大加速度加速的CACC-A都无法为换道车辆提供满足需求的换道间隙,导致车道1车辆在瓶颈路口排队停车,等待目标车道产生足够的安全换道间隙后开始换入目标车道,从而导致平均行驶速度降低以及平均通过时间增加.如表4所示,场景二中CACC-A的通行效率(62.62%)比CACC的通行效率(67.76%)更低,且在场景一中CACC-A的通行效率(89.83%)也比CACC的通行效率(92.32%)低,可见如果不能选择正确的加速策略和换道地点,盲目采用加速只能降低通行效率,而VFF-MSD模拟流体进行加速并选取合适的换道位置对通行效率有显著提升. 图13 场景二CACC,CACC-A,VFF-MSD算法车辆纵向位移 图14 场景二CACC,CACC-A,VFF-MSD算法车辆横向位移 表4 场景二中3种方法的性能结果 1) 本文提出了一种基于虚拟流场与MSD模型的道路拥堵缓解算法(VFF-MSD)来减少自动驾驶车辆通过瓶颈路段的通行时间.通过Ansys Fluent对建立的虚拟道路流场进行仿真分析,根据分析结果确定车辆的加速和换道策略,同时采用基于虚拟MSD的车辆协同换道模型,选用合适的参数保证车辆换道过程中的安全. 2) 在所提出的两个测试场景与CACC算法相比,VFF-MSD算法有更显著的性能提升,即有更高的平均速度和更短的通行时间.但在场景一中,采取加速策略的CACC-A性能比VFF-MSD更优,这是因为当车辆数较少时,更早地通过最大加速度进行加速可以获得更高的平均速度,从而缩短通行时间.但场景二表明,当车辆数增多时,这种加速策略会导致车辆在瓶颈路口处因无法产生足够的换道安全距离而形成排队拥堵,在场景二中VFF-MSD算法在各项参数上均优于CACC和CACC-A算法.合适的加速策略和换道位置以及协同换道算法是自动驾驶汽车快速通过瓶颈路段的关键. 3) 本文只考虑了所有车辆为自动驾驶车辆的场景并假定车与车之间的通信没有延迟和中断,并且为了便于计算对车辆的横纵向运动学建模进行了简化,未来将考虑建立更精确的安全距离模型和车辆运动学模型对参数进行进一步的优化.由于领队车需要跟踪虚拟流场流体的纵向速度,本文在建立虚拟MSD模型时未考虑系统对前方车辆的受力,如果在未来的研究中可以考虑换道车辆对前后车辆都产生影响的情况,对于换道时间和车辆的平均速度应该都会有进一步的提升.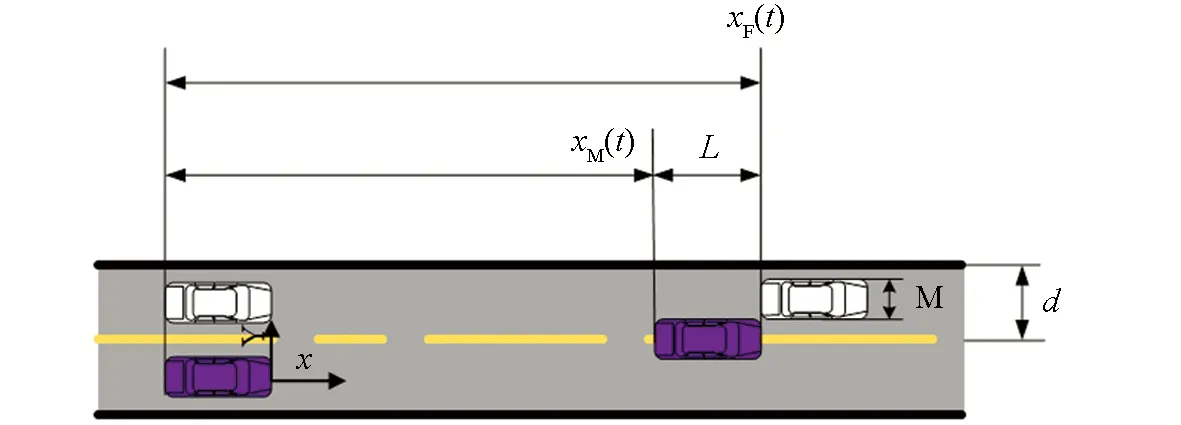

3 仿真分析
3.1 场景一仿真




3.2 场景二仿真


4 结论
