基于城轨电客车轴箱振动加速度的轨道短波不平顺识别方法

王凯峰，李明航，李玉路，吴宗臻，王小锁

（1.石家庄市轨道交通集团有限责任公司，河北石家庄 050000；2.中国铁道科学研究院集团有限公司城市轨道交通中心，北京 100081）

1 研究背景

轨道不平顺是轨道状态的重要评价指标，按照波长可以分为长波、中波及短波不平顺，是影响列车运行的安全性以及旅客舒适性的关键因素。轨道几何检测系统通常能识别2～150 m 内的中长波不平顺，但较难识别判断波长1 m 以下的短波不平顺。轨道短波不平顺往往由钢轨接头不平顺、焊缝、钢轨表面波浪磨耗等因素造成。列车的长期运行会导致相应部件疲劳损伤，轨道服役状态恶化，甚至会引发局部轨道结构破坏进而危及行车安全，危害较大。因此，钢轨短波不平顺的特征识别与治理一直是城市轨道交通领域关注的重点课题。图1为部分典型短波不平顺造成轨道服役状态恶化状态。

图1 短波不平顺造成轨道服役状态恶化

近年来，智能化运维已逐渐成为城市轨道交通（以下简称“城轨”）的发展趋势，《中国城市轨道交通智慧城轨发展纲要》明确提出，2025年城轨智能车辆占有率要达到95%以上，并且要实现车载各系统数据的采集、预警、远程监视及诊断分析，为车辆智能运维系统提供数据支撑，提高列车日常检修效率，降低列车运维成本。因此，有必要研究通过城轨电客车进行数据采集，精准识别短波不平顺关键特征，科学合理地评判钢轨状态，并根据状态情况进行维修。

由于轨道短波不平顺会导致列车运行时轴箱产生剧烈的高频振动，因此许多学者探索采用轴箱振动加速度来识别轨道短波不平顺的技术方法。刘金朝等提出采用轨道冲击指数评判轨道的短波不平顺状态的方法。牛留斌等在文献[2]基础上建立轮轨接触有限元模型，研究了特定轨道条件下钢轨波磨指数变化规律及其与轨道短波不平顺幅值之间的定量关系，给出相应的钢轨波磨指数限值；通过文献[4]详细总结了轴箱振动加速度的常用分析方法。徐晓迪等通过轴箱振动加速度数据获得了钢轨波磨典型波长，并基于快速傅里叶变换和频域积分的方法计算了波磨幅值。

既有研究表明，依据轴箱振动加速度数据计算的钢轨波磨指数可反映波磨的严重程度，但研究的绝大部分是针对速度高且较为均匀的高速铁路检测。对于城轨电客车运行速度较低、频繁加减速等运行特征，既有方法的适用性值得关注且需进行进一步研究。本文基于电客车轴箱振动加速度的实测数据，对文献[2]提出的波磨指数进行改进，使其能更准确地识别城轨中的短波不平顺，并结合时频分析技术分析得到波磨区段的典型波长。

2 利用轴箱垂向振动加速度评判轨道短波不平顺状态的方法

2.1 波磨指数概念及计算方法

轴箱振动加速度信号具有明显的随机性，从能量的统计指标出发，采用轴箱垂向振动加速度的运行有效值（Running RMS）可有效评判轨道的短波不平顺状态。同时，对分析结果的均值做归一化处理，可有效判别短波不平顺的阈值。根据参考文献[2]，轴箱垂向振动加速度有效值的快速计算方法：

式（1）中，S为轴箱垂向加速度有效值，m/s2；N为轴箱垂向加速度采样点数；i为轴箱垂向振动加速度的样本数，i= 1，2，…，N；a为带通滤波（10～1 000 Hz）后的轴箱垂向加速度，m/s2；K为移动计算有效值的窗长。

波磨指数为轴箱垂向振动加速度移动有效值与其平均值的比值，即：

式（2）中，TⅡ为波磨指数；Sr为测点r处轴箱垂向振动加速度的移动有效值，m/s2；为轴箱垂向振动加速度移动有效值的平均值，m/s2。

2.2 改进后的波磨指数计算方法

车辆通过钢轨波磨区段时，轮轨间产生高频的激励振动，激励频率f为：

式（3）中，f为激励频率，Hz；v为车辆通过速度，mm/s；λ为钢轨波磨区段轨道不平顺的波长，mm。

文献[2]的计算方法是面向运行速度较为均匀的轨道检测列车开发的，其速度固定条件下，通过带通滤波频段，即可获得较为稳定的某一特征波长段的振动响应，并由式（3）计算出所关心的频段。

然而，对于城轨电客车的实际测试条件，列车运行过程中频繁加减速且运行速度较低，难以采用统一的速度提取振动响应稳定的特征频率，并计算特征波长；另一方面，通过对短波不平顺的分波长统计分析，有利于初步判断不同测试区段的短波不平顺空间分布特征。因此，本文考虑了速度时变特性，将固定频率的检测指标改进为分波长控制，在文献[2]的研究基础上提出了改进的波磨指数。图2为改进波磨指数的计算示意图。

图2 改进的波磨指数计算示意图

首先给出2 个定义：将0.01～1 m 波长段对应的波磨指数定义为TⅡ，total；参考BS EN 13231-3 : 2012 规定的分析指标，将短波不平顺波长划分为0.3～1 m，0.1～0.3 m，0.03～0.1 m，0.01～0.03 m，将这4 段波长区间对应的波磨指数分别定义为TⅡ，λ1，TⅡ，λ2，TⅡ，λ3，TⅡ，λ4。

改进后的波磨指数计算过程如下：

（1）划分测试数据，选取分析窗长为1 s，并设置合适的重叠系数（本文选定为19/20）；

（2）将短波不平顺波长划分为0.3～1 m，0.1～0.3 m，0.03～0.1 m，0.01～0.03 m 4 段，依据不同分析窗的实时的1 s 内平均速度，计算各波长所对应的频段；

（3）依据上述计算到的频段，对实测的各测点处轴箱垂向振动加速度进行带通滤波截取；

（4）计算滤波后各测点处各波段轴箱垂向振动加速度的移动有效值Sr，λi；

（5）计算全部测点处轴箱垂向振动加速度的移动有效值的平均值，即为标定参数 ；

（6）计算各测点的总的波磨指数TⅡ，total及分波长波磨指数TⅡ，λi。

3 计算结果对比分析

3.1 波磨指数分析结果

利用原有的频率控制方法和本文改进的波长控制方法对城轨电客车的轴箱垂向振动加速度进行分析，以诊断轨道的短波不平顺状态，并对2 种方法的分析效果进行对比。

实测列车通过某城轨区段内轴箱垂向振动加速度原始波形及计算得到的波磨指数如图3所示。参考波磨指数的计算公式（2），理想状态下，全分析区段的波磨指数应趋近于1。由图3可以看出，原有的通过关心频率（10～1 000 Hz）控制方法计算的波磨指数在匀速阶段（35～60 s）能准确的定位钢轨波磨区段，在变速阶段（80～100 s），轴箱振动加速度明显放大，但传统波磨指数并未发生显著的突变。本文提出的改进后的波磨指数更能凸显该区段的钢轨粗糙状态变化。此外，在25～30 s 及108～115 s 范围内的分析结果显示，改进的钢轨波磨指数可有效抑制钢轨接头等引起的瞬时振动响应的统计结果。

图3 波磨指数分析结果对比

图4给出了分波长波磨指数统计结果。显然，分波长波磨指数可以更明确地分析波磨区段的显著波长。35～60 s 内的波磨区段主要为300～1 000 mm、10～100 mm 波长的波磨，100～300 mm 波长的波磨指数在全时段接近1。80～100 s 内的波磨区段特征波长则主要分布在10～100 mm 范围。10～30 mm 段的波磨指数波动趋势与30～100 mm 的相似，这是由于钢轨波磨会激励起典型波长控制频率的倍频响应，该波长段的振动响应是对应20～60 mm 波长引起的。

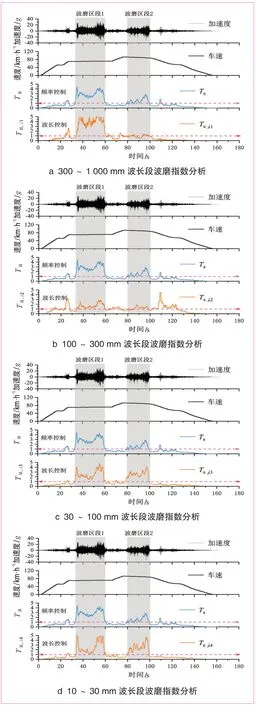
图4 不同波长段波磨指数分析结果

3.2 特征波长提取

通过改进后的波磨指数可以有效定位发生钢轨波磨的区段，时频分析方法则可以提供时间域与频率域的联合分布信息。通过时频分析技术，可将非平稳信号表示为时间和频率的二维函数，能更加直观地描述信号频率随时间变化的关系。常见的时频分析方法有短时傅里叶变换（STFT）、小波变换（WT）以及希尔伯特黄变换（HHT）等。

截取35～60 s 及80～100 s 2 个发生钢轨波磨区段的振动响应进行时频分析，得到实测振动响应的时频分布特征，如图5所示。参考图5拾取不同时刻的特征频率，综合考虑提取得到的特征频率及实测车速，由式（3）可计算典型波长。

图5 时频分析得到的三维谱阵

图6a 及6b 分别为35～60 s，80～100 s 的区段内特征频率和典型波长的分析结果。从图6可以看出，在35～60 s 内有2 个特征频率为50 Hz 和400 Hz 左右，对应2 个典型波长为370 mm 和50 mm 左右；在80～100 s 区段内特征频率为400 Hz 左右，对应典型波长为60 mm 左右。

图7及图8分别给出了区段2 的钢轨波磨情况的现场调研结果，其1/3 倍频程波长中心波长为63 mm，与图6b 给出的分析结基本一致。因此，本文提出的计算分析方法对城轨电客车频繁加减速、运行速度较低的特点具有较好的适用性，在有效提取波磨病害发生区段的同时，结合时频分析技术可准确提取特征波长。

图6 特征频率和特征波长拾取结果

图7 现场钢轨波磨照片（区段2）

图8 实测钢轨表面粗糙度级（区段2）

4 结论

为提升城轨钢轨波磨病害的检测效率，本文基于电客车轴箱振动加速度的实测数据，提出了改进后的波磨指数计算方法。该方法能够反映波磨发生区段的钢轨粗糙状态，并且可以有效抑制钢轨接头等引起的瞬时冲击对检测结果的影响；以分波长段波磨指数作为初步判断依据，结合时频分析技术，可准确提取钢轨波磨的特征波长信息。针对城轨电客车运行速度较低、频繁启停的运行特征，本文的方法具备良好的适用性。