限制Heisenberg李超代数的限制上同调
2023-01-16郝博茹远继霞
郝博茹,远继霞
(黑龙江大学数学科学学院,黑龙江 哈尔滨 150080)
0 引言
李代数与李超代数在数学和物理学中都起着重要的作用.限制李代数和限制李超代数在李代数及李超代数理论中占据着重要的地位.李(超)代数的上同调是研究拓扑学、光滑向量场、全纯函数等领域问题的重要工具.文献[1]给出了李代数的标准复形;文献[2]给出了李代数的上同调理论;文献[3]首次构造出限制李代数的限制上同调.近年来,限制李代数的限制上同调理论引起了许多研究者的兴趣[4-5];文献[6-7]介绍了李超代数的上同调;在限制李代数的限制上同调理论的基础上,学者进一步研究了限制李超代数的限制上同调[8-9];Heisenberg李超代数是一类重要的幂零李超代数,对于其上结构的研究引起众多学者的兴趣;文献[10]证明了具有偶中心的Heisenberg李超代数同构于超外代数的商代数,并且具有奇中心的Heisenberg李超代数同构于超外代数的直和;文献[11]提出Heisenberg李超代数的中心扩张;文献[12]计算出了2维Heisenberg李超代数的Heisenberg的Rota-Baxter算子.
本文研究了Heisenberg限制李超代数的系数取自1维平凡模的1,2维限制上同调.给出了具有偶(奇)中心的Heisenberg李超代数的限制结构,使其成为一个限制李超代数,计算了具有偶(奇)中心的限制Heisenberg李超代数的系数取自1维平凡模的1,2维限制上同调,并计算了系数取自伴随模的1阶限制上同调.
1 预备知识

文献[13]指出Heisenberg李超代数分为具有偶中心的Heisenberg李超代数Hm,n和具有奇中心的Heisenberg李超代数Hn:
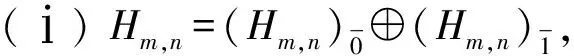

关于李超代数上同调的概念以及李超代数的限制上同调,详细的定义可参考文献[8-9].
设L是一个李超代数,且M是一个L-模,当q>0时,令Cq(L;M)=Hom(ΛqL,M),这里ΛqL为L的q次超外积;当q=0时,令Cq(L;M)=Hom(F,M)≅M;当q<0时Cq(L;M)=0.
下面给出计算需要的相关公式:
(1)
ind1(φ)(x)=φ(x[p])-xp-1φ(xp);
(2)
(3)
2 系数取自1维平凡模的限制Heisenberg李超代数的限制上同调

为了计算方便,分别给出Hm,n和Hn的系数取自1维平凡模的上链复形的基底.Hm,n的系数取自1维平凡模的上链复形的基底如下:
C0(Hm,n;F)Ω0={1},C1(Hm,n;F)Ω1={ui,z*,ωj|1≤i≤2m,1≤j≤n},
C2(Hm,n;F)Ω2={ui,j,ωk,l,usz*,usωj,z*ωk|1≤i,j,s≤2m,i C2(Hm,n;F)Ω3={ui,j,k,ωr,s,t,ua,bz*,ua,bωe,ucωe,f,ucz*ωe,z*ωe,f|1≤i,j,k,a,b,c≤2m, i Hn的系数取自1维平凡模的上链复形的基底如下: C0(Hn;F)Ω0={1},C1(Hn;F)Ω1={vi,z*,ωj|1≤i,j≤n}, C2(Hn;F)Ω2={vi,j,ωk,l,z**,vsz*,vsωk,z*ωk|1≤i,j,s≤n,i C3(Hn;F)Ω3={vi,j,k,ωr,s,t,z***,va,bz*,vcz**,z**ωe,z*ωe,f,va,bωr,vcωe,f,vcz*ωe| 1≤i,j,k,a,b,c≤n,i Hm,n的系数取自1维平凡模的限制上链复形的基底如下: Hn的系数取自1维平凡模的限制上链复形的基底如下: 由(1)式直接计算可得如下引理: 结论(ⅱ)证明方法与结论(ⅰ)类似,此处略去. 故由引理2.1可知结论成立. 由(3)式有 结论(ⅱ)证明方法与结论(ⅰ)类似,此处略去. 引理3.1[14](ⅰ)设D是Hm,n的偶线性变换,则D是Hm,n的超导子,当且仅当D在标准基下的矩阵形式为 其中:A为任意m阶方阵;B,C为任意m阶对称矩阵;R为任意n阶反对称矩阵;M,E为任意1×m阶矩阵;λ∈F.并且有 (ⅱ)设D是Hm,n的奇线性变换,则D是Hm,n的超导子,当且仅当D在标准基下的矩阵形式为 其中J,K为任意n×m阶矩阵,并且有 经过简单计算易得到如下定理: 定理3.1 (ⅰ)在标准基下,Hm,n内导子的基底为 {e2m+1,i,e2m+1,i+m,e2m+1,f+2m+1|1≤i≤m,1≤f≤n}. (ⅱ)在标准基下,Hn内导子的基底为 {e2n+1,i+n,e2n+1,i|1≤i≤n}. 定理3.2 (ⅰ)系数取自伴随模的具有偶中心的Heisenberg李超代数的一维限制上同调为 (ⅱ)系数取自伴随模的具有偶中心的Heisenberg李超代数的一维限制上同调为 证明(ⅰ)设D∈Der(Hm,n),采用引理3.1中的符号.先证D是一个限制导子,当且仅当λ=0.当D∈Der(Hm,n)时由引理3.1有D(z)=2λz.D是一个限制导子,当且仅当 当D∈Der(Hm,n)时由引理3.1有D(z)=0,则 从而D是一个限制导子,结论成立. 故Hm,n的限制导子在标准基下的矩阵形式为 其中:A为任意m阶方阵;B,C为任意m阶对称矩阵;F为任意n阶反对称矩阵;M,E为任意1×m阶矩阵;λ∈F;F为任意1×n阶矩阵;J,K为任意n×m阶矩阵.故 Derres.(Hm,n)=spanF{ei,j-ej+m,i+m,es+m,t+et+m,s,es,t+m+et,s+m,ei,i+m,ei+m,i, ek,l-el,k,ef+2m+1,i-ei+m,f+2m+1,ef+2m+1,i+m+ei,f+2m+1,e2m+1,i, e2m+1,i+m,e2m+1,f+2m+1|1≤i,j≤m,1≤s,t≤m,2m+2≤k≤l≤2m+1+n,1≤f≤n}. 由引理3.2和定理3.1可得结论. 结论(ⅱ)证明方法与结论(ⅰ)类似.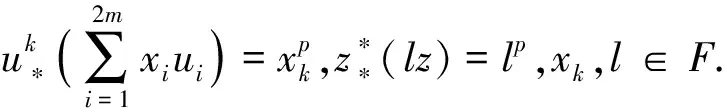
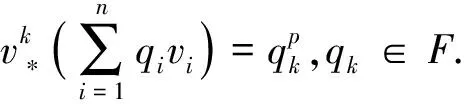

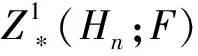


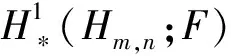

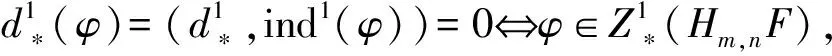
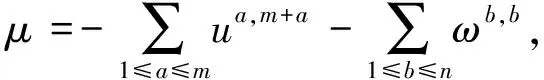
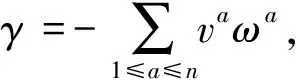
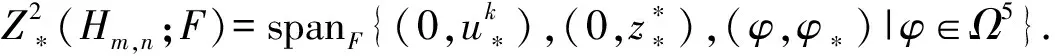

3 系数取自伴随模的限制Heisenberg李超代数的限制上同调

