基于模糊自适应PID的应急救援机器人电机控制系统设计
2023-01-16胡兴志刘伟佳李娟娟
胡兴志,刘伟佳,李娟娟
(1.华北科技学院 应急装备学院,北京 东燕郊 065201;2.河北省矿山设备安全监测重点实验室,北京 东燕郊 065201;3.华北科技学院 矿山安全学院,北京 东燕郊 065201)
0 引言
我国自然灾害和生产安全形势十分严峻,地震、山火、泥石流、水患多发,石油化工企业规模不断扩大,风险指数成倍上涨,灾后应急救援难度增加。现急需运用大数据、人工智能等新兴技术,全面提升现代化应急能力[1]。应急就是与时间的赛跑,现代化、智能化应急装备的配备使用至关重要,“机器换人”势在必行,无人系统装备不断完善,不仅提高应急救援效率,还可以减轻救援人员的伤亡情况。
随着科技水平的迅猛发展,依托各项综合技术成果研制的高灵活性能应急救援机器人,逐步走进大众视野,成为救援指战员的新宠。机器人加入应急救援的主战场,进入应急救援人员无法抵达的灾害事故现场,第一时间获取现场信息,开展救援工作,是提高应急救援能力的有效手段,在应急救援领域中得到了广泛关注与应用。日本福岛核事故,先后有30多种不同类型的机器人用于事故处置[2];四川雅安芦山地震,沈阳自动化研究所科研人员携带废墟可变形搜救机器人急赴灾区开展救援工作[3],这都展现出了应急救援机器人高效、灵活、精准的优势。
电机作为机器人的运动驱动装置,高精度的电机控制是衡量应急救援机器人性能的重要指标。目前,高精度机器人大多采用伺服电机驱动系统,但成本较高。近年来,步进电机以其结构简单、分辨率高、价格低等优势闯入研发人员的视野。但是,步进电机是非线性、时变的控制对象,环境干扰因素较多,传统PID控制很难达到理想控制效果[4]。为提高电机运行性能,确保应急救援机器人安全、稳定、高效、精准地运行,新型优化改进控制策略陆续出现,一种是变结构PID控制,另一种是智能控制,如神经网络控制、滑模控制、模糊控制等。对于非线性、时变的控制对象,模糊控制有良好的控制效果[5],鲁棒性也很好。但是单独采用模糊控制,很难完全消除稳态误差。将传统PID控制和模糊控制相结合,构成模糊自适应PID控制,能够达到动态性能好、稳态无偏差的控制效果,还解决了传统PID控制无法在运行过程中进行参数自整定的难题,拥有了更好的控制品质,系统也得到了进一步的优化。若系统中出现扰动时,PID参数也能自动修正[6]。
针对步进电机调速系统,设计模糊自适应PID控制器,运用MATLAB/Simulink软件,对传统PID电机控制系统和模糊自适应PID电机控制系统进行对比分析。
1 模糊控制
模糊控制系统如图1所示。模糊控制器由4个部分构成。
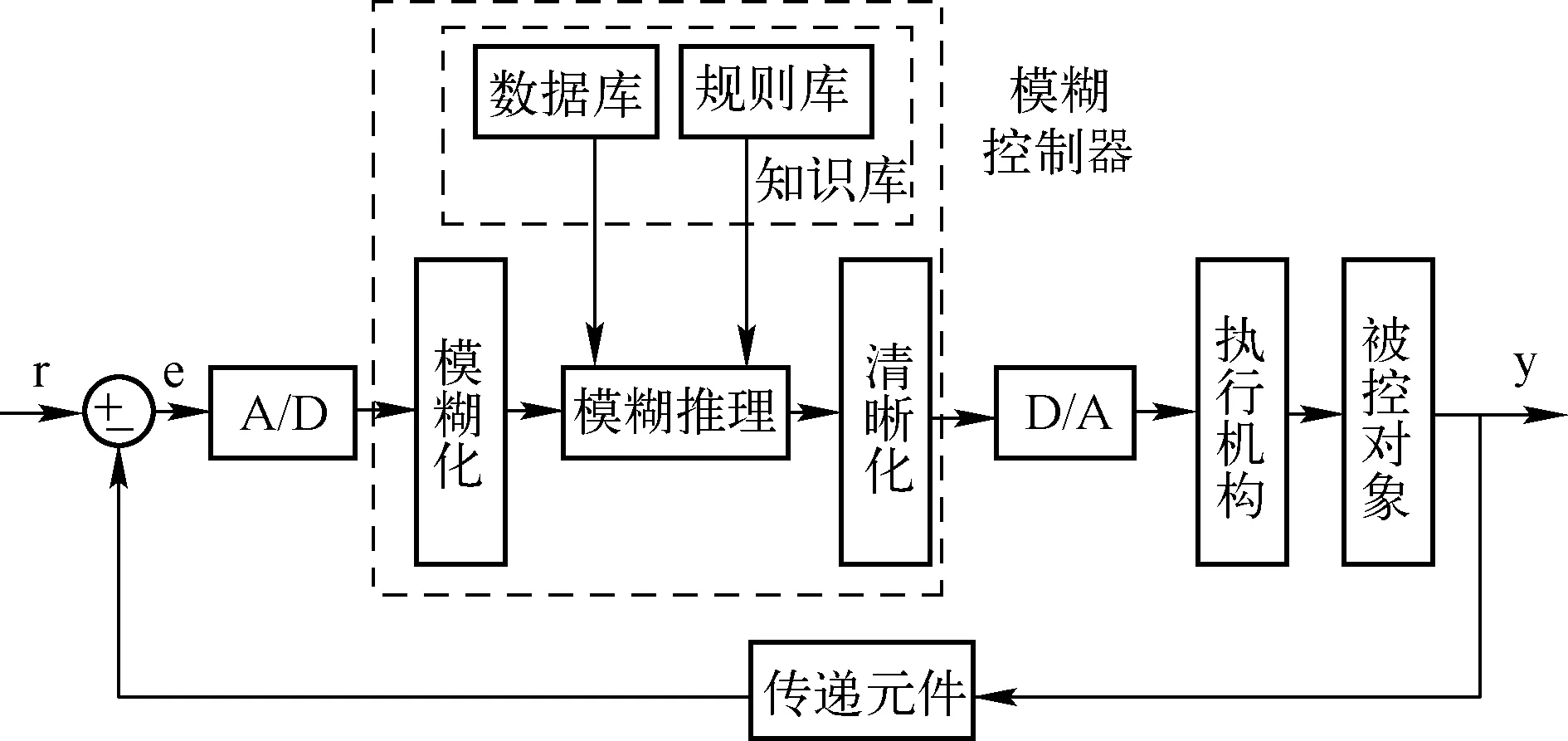
图1 模糊控制系统工作原理
(1) 模糊化
在选定的模糊论域内,将精确数值转变为模糊语言变量值,形成模糊集合。
(2) 知识库
知识库包括存放数据的数据库和存放模糊控制规则的规则库。
(3) 模糊推理
根据模糊规则,对输入信号进行模糊推理,得到相应的输出值。
(4) 清晰化
清晰化也称为解模糊化,相当于模糊化的逆运算,将用模糊语言表示的输出值转化为精确值。
2 模糊自适应PID控制
控制系统如图2所示。
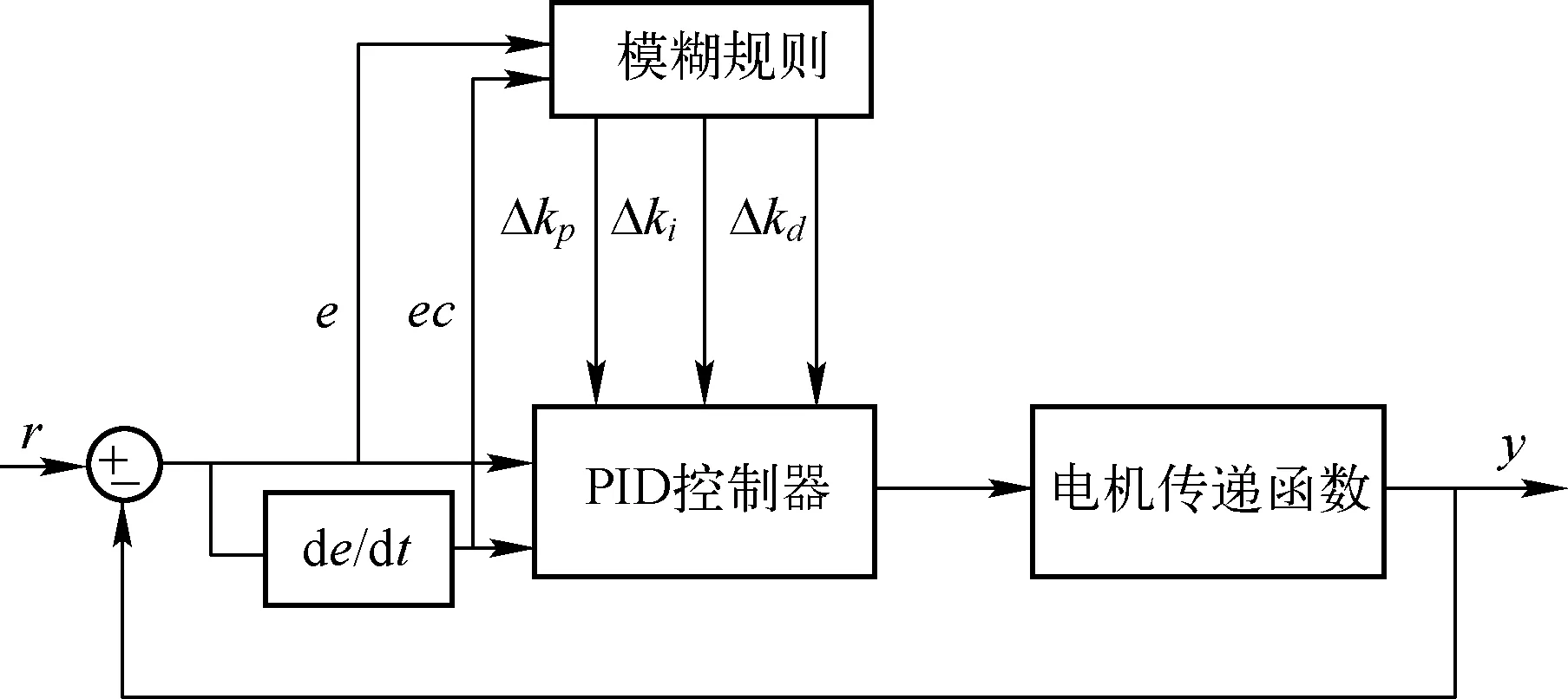
图2 模糊自适应PID电机控制系统
设计思想:利用选定的模糊规则,对实时检测到的输入,系统设定值r与系统输出值y之间的偏差e和偏差变化率ec,进行模糊推理,得到这一时刻的输出,Δkp、Δki、Δkd,在运行过程中实时在线整定PID控制器参数kp、ki、kd,以实现更好的控制效果。
PID参数整定原则为:
比例调节系数
kp=kp0+Δkp
(1)
积分调节系数
ki=ki0+Δki
(2)
微分调节系数
kd=kd0+Δkd
(3)
式中,kp0、ki0、kd0为PID控制器初始值。
e、ec为输入,Δkp、Δki、Δkd为输出,选用‘两输入三输出’结构。
(1) 模糊化
e、ec对应模糊变量E、EC,Δkp、Δki、Δkd对应模糊变量ΔKp、ΔKi、ΔKd,E、EC、ΔKp、ΔKi、ΔKd的模糊论域均选取[-6,6],将其划分为7个对称的模糊集合:NB、NM、NS、ZO、PS、PM、PB。模糊语言变量表示为:负大、负中、负小、零、正小、正中、正大,选取三角形隶属函数对其进行表示。
e的量化因子[7]为:
(4)
式中,xe为e的基本论域;n为e的模糊论域。
ec的量化因子[7]为:
(5)
式中,xec为ec的基本论域;m为ec的模糊论域。
(2) 模糊规则
模糊规则就是将操作人员们的实践经验,用模糊语言变量值进行归纳总结出来的规律。设计模糊规则应当遵循以下原则:当误差大时,要把消除误差作为首要任务,迅速减小误差;当误差小时,消除误差和保证系统稳定要同时兼顾。
控制规则用IF-THEN语句表达,ΔKp、ΔKi、ΔKd控制规则见表1[8]。
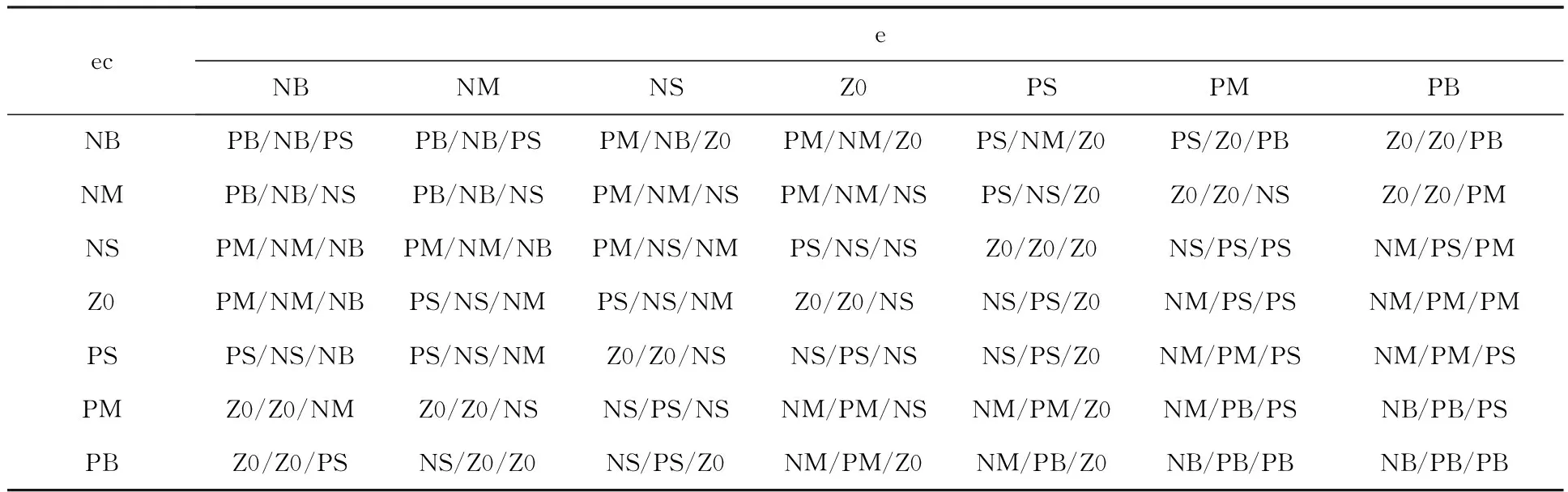
表1 ΔKp/ΔKi/ΔKd控制规则
(3) 模糊推理及清晰化
模糊推理采用Mamdani法,清晰化采用重心法。
输出变量的比例因子[7]为:
(6)
式中,yu为输出变量的基本论域;a为输出变量的模糊论域。
3 电机控制系统Matlab仿真实验
使用MATLAB软件中的Simulink进行仿真实验研究。选用57步进电机作为被控对象,传递函数如下[9]:
(7)
3.1 传统PID电机控制系统仿真
控制系统仿真如图3所示。对于PID控制系统的控制效果而言,kp、ki、kd三个参数值的整定是核心。根据kp、ki、kd对系统性能的影响,秉承着先比例,后积分,再微分的先后顺序,进行反复调整,直至最终整定出最佳的PID控制参数值kp=2.8、ki=5、kd=1,使系统实现最优控制,同时兼顾稳定性、准确性和快速性。
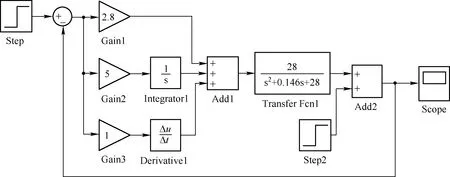
图3 传统PID电机控制系统仿真
3.2 模糊自适应PID电机控制系统仿真
控制系统仿真如图4、图5所示。将PID控制器初始值设为kp=2.8、ki=5、kd=1。
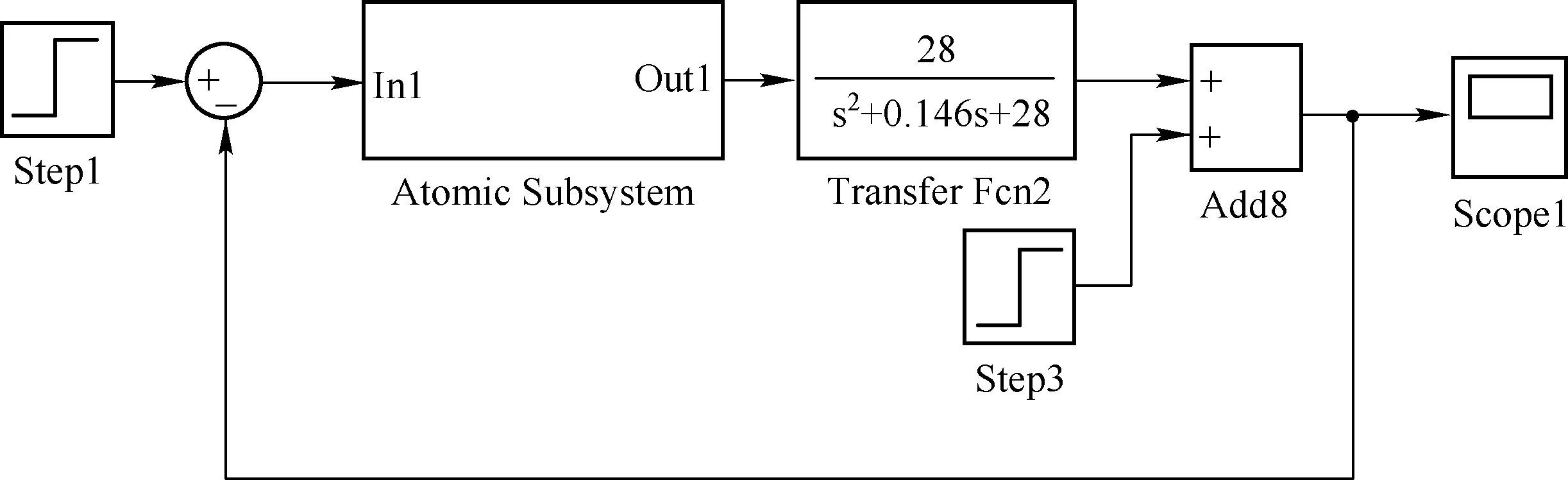
图4 模糊自适应PID电机控制系统仿真

图5 模糊自适应PID控制器子系统仿真
在MATLAB软件中运行fuzzy函数,弹出Fuzzy Logic Designer窗口,根据设计的模糊自适应PID控制器来编辑,首先设置两输入,三输出的模糊控制器结构,模糊推理选用mamdani方法,清晰化选用centroid方法,然后在Membership Function Editor窗口中,将模糊论域设置为[-6,6],添加7个类型选定为trimf的隶属函数,最后在Rule Editor中填入设计好的49条模糊规则。整体编辑过程如图6、图7、图8所示。
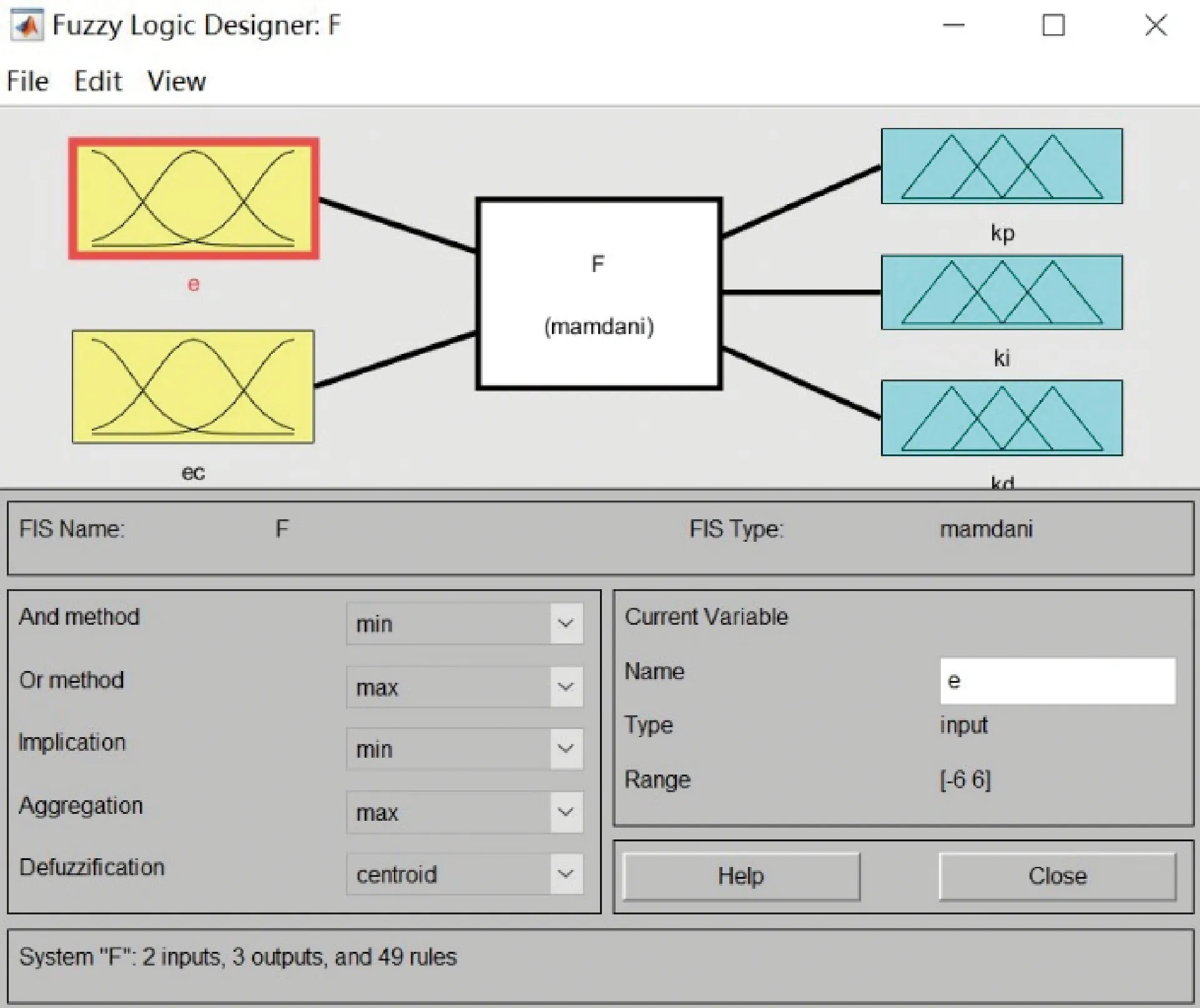
图6 模糊逻辑设计器
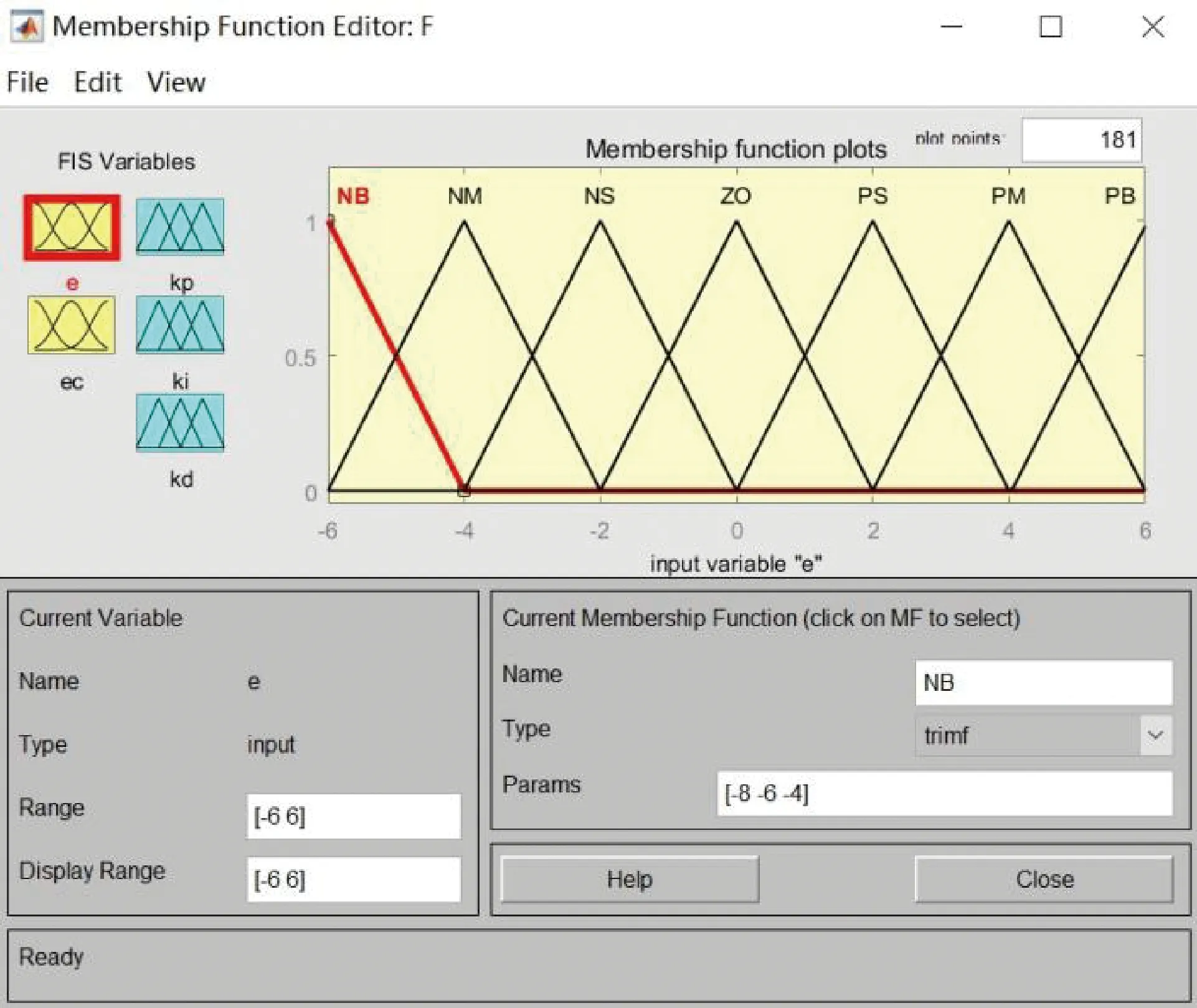
图7 隶属函数编辑器

图8 模糊规则编辑器
ΔKp、ΔKi、ΔKd模糊规则如图9、图10和图11所示。编辑完成后,保存至工作区,并加载至Fuzzy Logic Controller模块中。
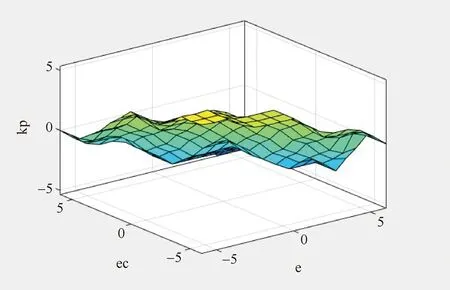
图9 ΔKp模糊规则
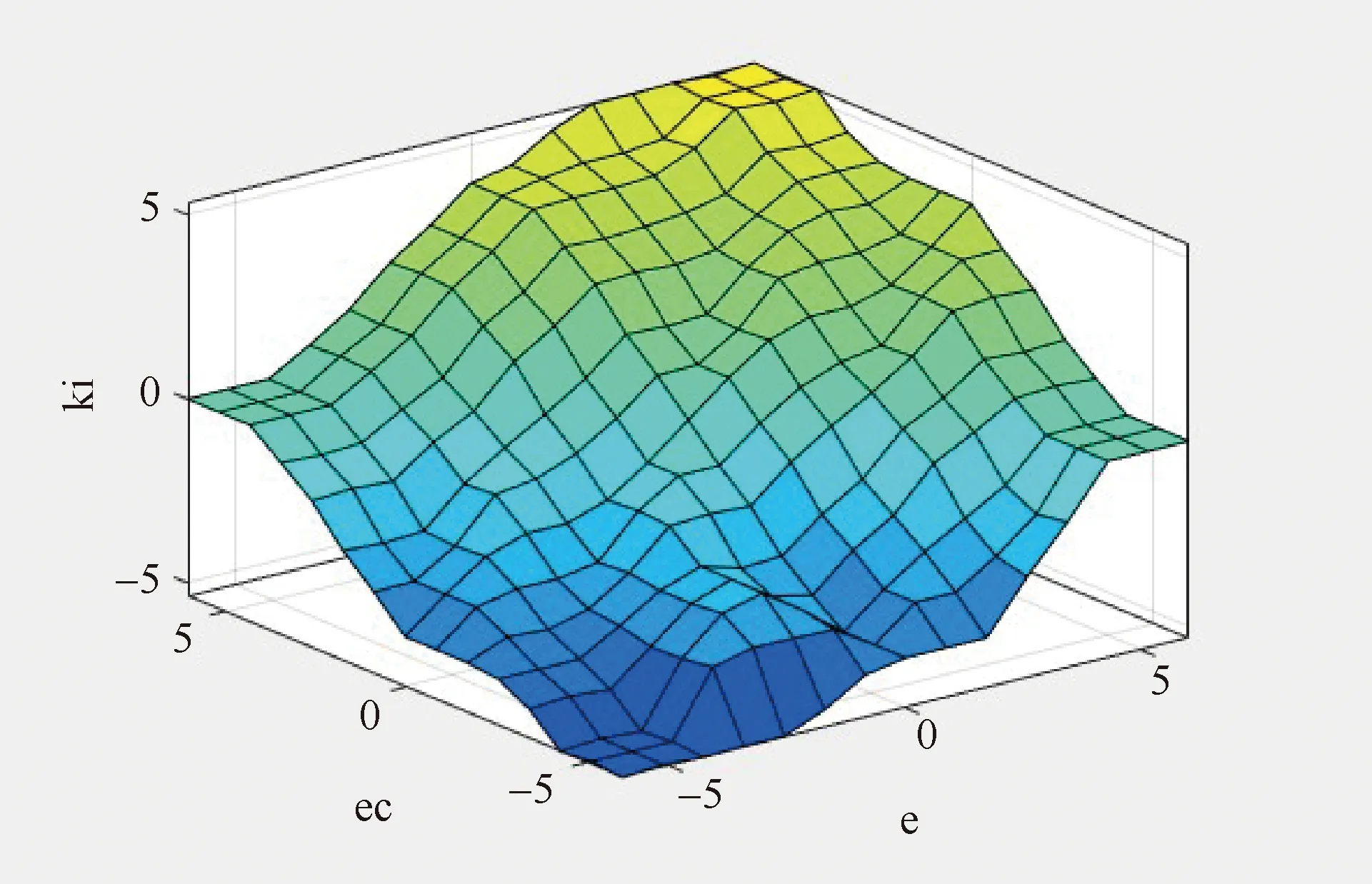
图10 ΔKi模糊规则
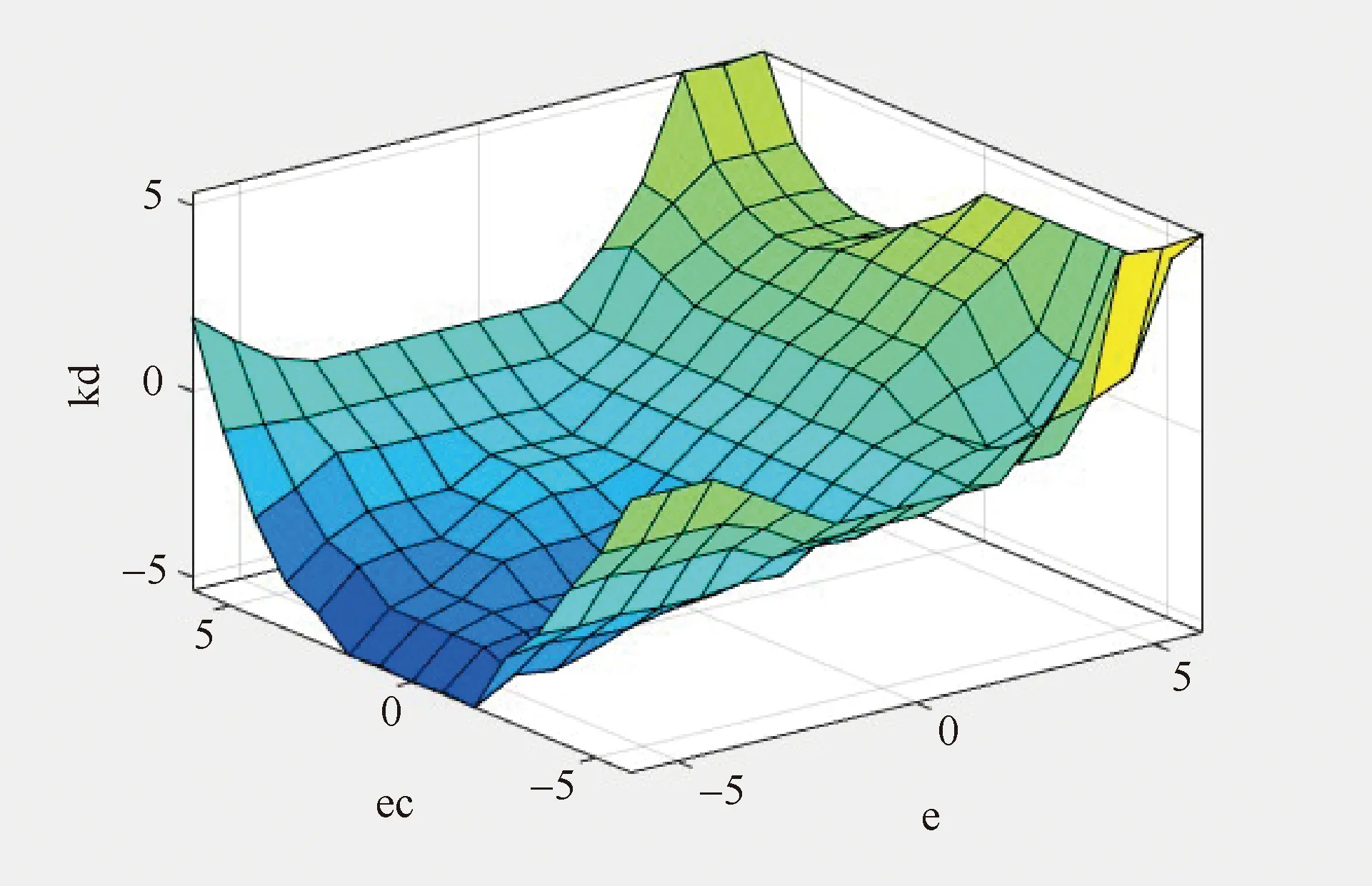
图11 ΔKd模糊规则
3.3 仿真结果对比
控制系统输出曲线如图12所示,性能指标见表2。
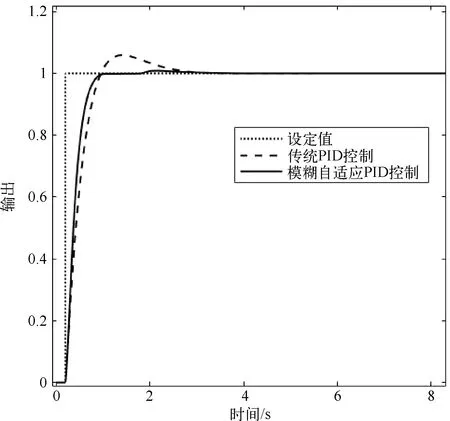
图12 控制系统输出曲线对比
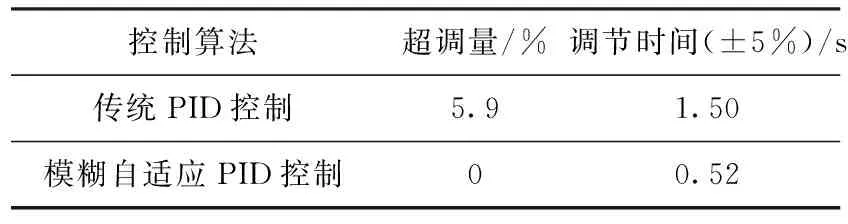
表2 性能指标对比
对比分析可得,模糊自适应PID电机控制系统拥有更好的控制效果,响应速度更快、超调量更小、调节时间更短。
不同于理想实验状态,应急救援机器人在真正投入使用时,应用场所环境复杂多样,有着很多干扰因素的存在。为验证系统的抗干扰能力,在仿真6s时,加入外部干扰信号,控制系统输出曲线对比如图13所示。从图13中可以看出,模糊自适应PID电机控制系统抗干扰能力更强,在系统有外部干扰信号的扰动时,有着更好的控制效果,响应速度更快、超调量更小、调节时间更短。
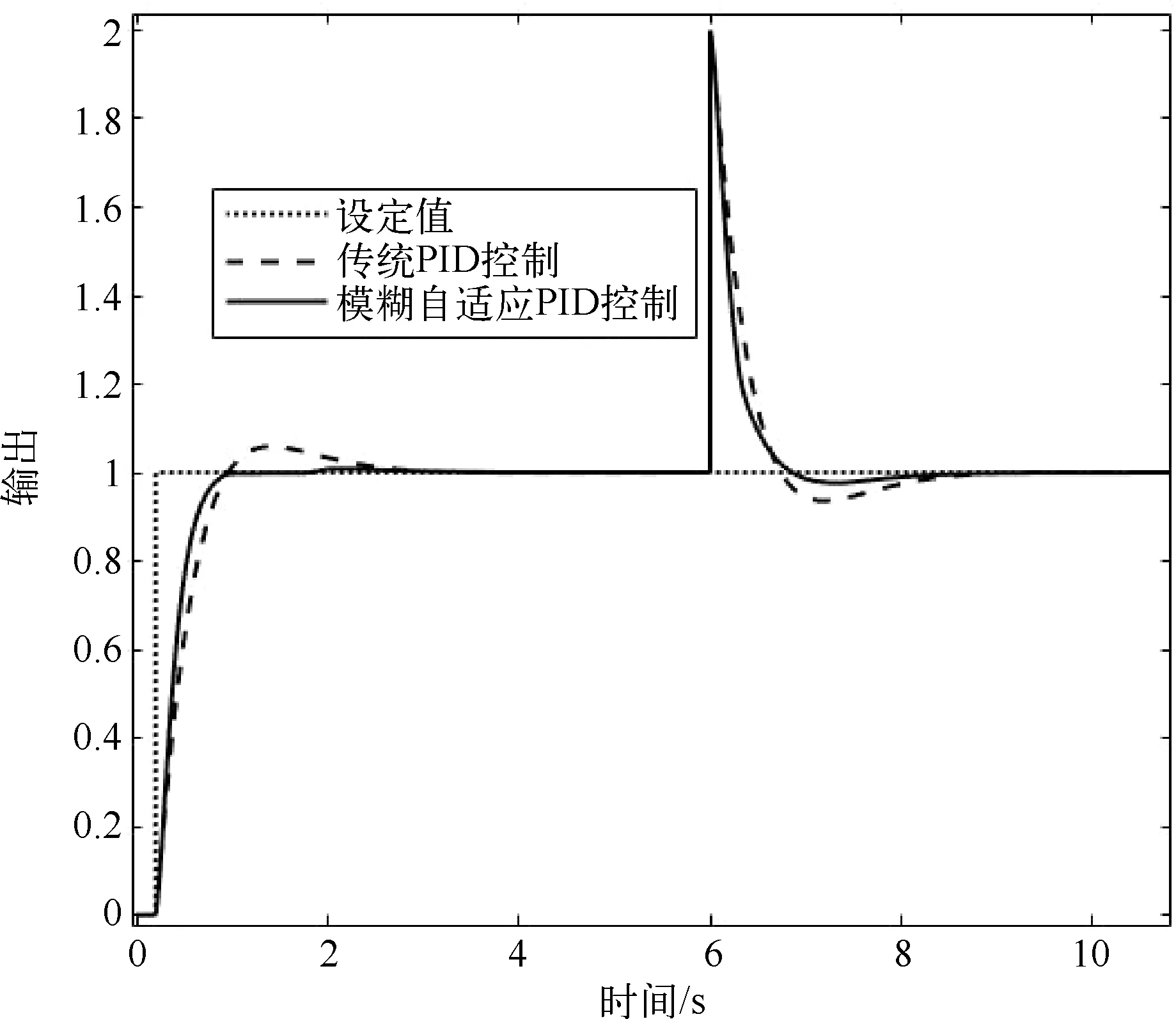
图13 加入干扰后的系统输出曲线对比
4 结论
(1) 步进电机是非线性、时变的控制对象,对于步进电机应用模糊自适应PID控制,不仅可以达到动态性能好,稳态无偏差的控制效果,而且还可以在运行过程中进行参数自整定。
(2) 针对应急救援机器人的步进电机控制系统,进行MATLAB仿真实验。结果表明,模糊自适应PID电机控制相比于传统PID电机控制,拥有更好的控制效果,响应时间更快、超调量更小、调节时间更短,抗干扰能力更强。
