基于自适应Boosting组合模型的空气质量预测*

徐海峰，黄小莉，张 政

(西华大学 电气与电子信息学院，四川 成都 610000)

0 引言

空气污染是当今世界面临的十分严峻的问题，不仅对人体健康存在严重威胁，还对户外活动产生限制。空气质量指数(Air Quality Index，AQI)，是衡量空气质量的关键指标。通常而言，AQI的数值越大，表明空气的污染越严重，对人体的危害愈大。

目前而言，许多高校和企业在空气质量预测方面做了大量的研究。例如，华中科技大学韦德志在2009年使用BP神经网络对华中某市空气质量进行预测，能准确分析出主要污染因子及其日平均浓度[1]；河北科技大学张冬雯团队在2020年提出了基于长短期记忆单元(LSTM)的神经网络模型，成功预报了美国休斯顿和印度德里地区的空气质量水平，结果优于使用BP神经网络[2]；中国科学院沈阳计算技术研究所祁柏林团队在2021年提出了基于GCN和LSTM的空气质量预测模型，分别提取小微型监测站之间的空间特征和特征并综合时空特征进行预测，结果要优于LSTM神经网络[3]；上海师范大学赵前矩等在2022年提出RF-CRNN模型预测上海市空气质量，使用随机森林(Random Forest，RF)算法选择特征，使用CRNN模型预测取得良好效果[4]；Du Shengdong等提出了一种基于一维CNNs和Bi-LSTM的联合混合深度学习框架，用于多元空气质量相关时间序列数据的共享表示特征学习，预测PM2.5具有较高的准确性[5]；Yan Rui等提出建立多时间多站点深度学习模型(LSTM，CNN，CNN-LSTM)预测北京每小时空气质量取得良好效果[6]。

上述研究中采用的大多是单一的或改进的神经网络模型，而单一的模型的优势与局限性各不相同，一定程度上会影响整体的预测效果。本文提出一种自适应Boosting组合模型应用于空气质量预测领域，对于充分发挥单一模型的优势，提高预测准确性具有重要意义。

1 模型框架

1.1 自适应Boosting组合模型

受到医院“会诊”机制的启发，提出一种自适应的Boosting组合模型。将Boosting模型中的XGBoost模型、LightGBM模型和AdaBoost模型作为基础模型，采用误差平方和倒数法等五种方法，根据三个模型在当前预测任务上的预测精度自适应地分配权重，如同医生会诊，医生的话语权根据病人病情和医生擅长的领域分配。自适应Boosting组合模型旨在充分利用三个模型优势，提高空气质量的预测精度。

将获取的实验数据输入，采用简单加权平均法、有效度确定权重系数法、误差平方和倒数法、标准差法、等权重法，根据三个基础模型的预测精度自动分配其所占权重，将三个模型的预测结果乘以权重再叠加，得到最终的预测值。自适应Boosting组合模型流程图如图1所示。

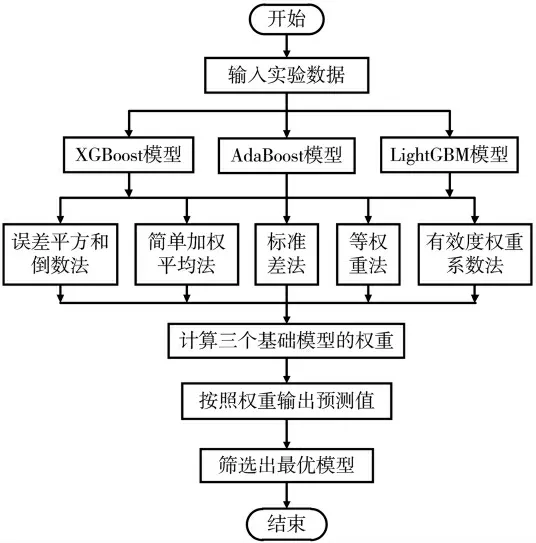
图1 空气质量组合预测模型流程图

XGBoost模型是由华盛顿大学陈天奇博士在2016年提出的一种Boosting模型。与传统GBDT算法相比，利用二阶泰勒公式展开损失函数、在目标函数中加入正则化项[7]等方法提升了运行速度和分类效果。LightGBM是微软在2017年发布的基于决策树算法的改进框架。相比于其他的Boosting集成方法，其训练速度更快，内存占用更少，在面对大样本高纬度数据时耗时较少。自适应增强算法简称AdaBoost算法，是目前被广泛使用的Boosting算法之一，具有较高的检测速率和不易出现过适应现象等优点[8]。

1.2 模型组合方法

1.2.1 误差平方和倒数法

误差平方和倒数法是指根据基础模型在预测任务误差平方和来确定基础模型权重，计算公式如式(1)所示，子模型的误差平方和越小，说明预测效果越好，所占的权重越高。

式中SSEk表示第k个子模型的误差平方和，ωk表示第k个子模型所占的权重。

1.2.2 简单加权平均法

将每个基础模型的误差平方和按照降序排列，误差平方和越大的模型排名越靠前，排名越靠前的模型分配的权重越小，计算公式如下：

式中ei表示第i个基础模型的排名，ωk表示第k个子模型所占的权重。

1.2.3 有效度确定权重系数法

预测有效度是反映预测精度的有效指标之一，根据模型精度大小对其预测能力进行有效度测定[9]。计算有效度需先求出子模型的预测精度序列，再分别求出精度序列的均值与标准差，如式(3)所示。

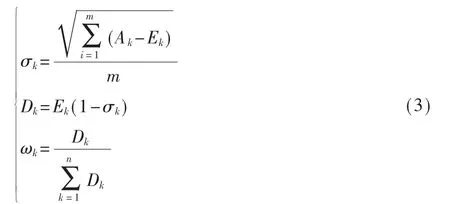
式中Ak表示第k个子模型的预测精度序列，Ek表示第k个子模型的精度序列的均值，而σk表示的是第k个子模型的精度序列的方差，Dk为第k个子模型的预测有效度，ωk为第k个子模型所占的权重。

1.2.4 等权重法

等权重法是指每个子模型的权重相同，如式(4)所示。

式中N表示基础模型的总数，ωk表示第k个子模型所占的权重。

1.2.5 标准差法

标准差是方差的均方根值，也代表着模型的预测值与真实值的偏离情况，根据标准差确定子模型的权重，标准差越小，所占的权重就越大，计算公式如下：

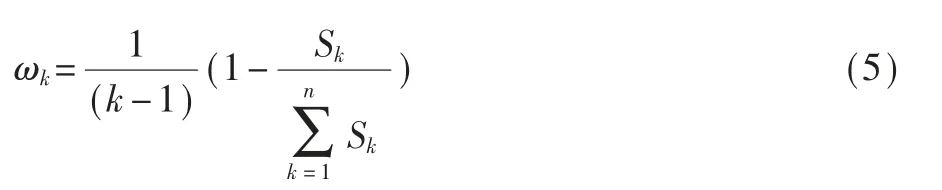
式中Sk代表第k个子模型的标准差，ωk表示第k个子模型所占的权重。

1.3 模型评价指标

为了直观反映自适应Boosting组合模型在空气质量预测领域的效果，选择平均绝对误差(MAE)、决定系数(R2)、均方根误差(RMSE)三个指标评价模型预测效果，计算公式如下。

式中y(i)表示样本实际值，y^(i)表示样本预测值，yˉ表示样本实际平均值。MAE、RMSE描述的是样本实际值与模型预测值的偏离程度，两者均越小越好；R2用于判断预测值与真实值的拟合情况，越接近于1越好。

2 实验设计

2.1 数据来源与实验环境

实验数据是从空气质量监测平台上获取到的中 国 某 城 市2020年7月13日0：00到2021年7月13日0：00的空气质量数据。去除缺失值后共计8 506条，数据集中的指标信息如表1所示。实验环境为电子信息实验室，仿真软件为Python 3.9，计算机处理器为i5-12400，内存为16 GB，操作系统为Windows 11。

表1 实验数据指标信息表

2.2 特征选择

特征选择能够提高学习算法性能和数据泛化能 力[10]。本 文 使 用RF、XGBoost和LightGBM三 种 模型对数据集的所有特征进行重要性排序，为了保证特征选取结果全面，将根据三种算法排序的综合结果进行选择特征，特征重要性排序如表2所示。

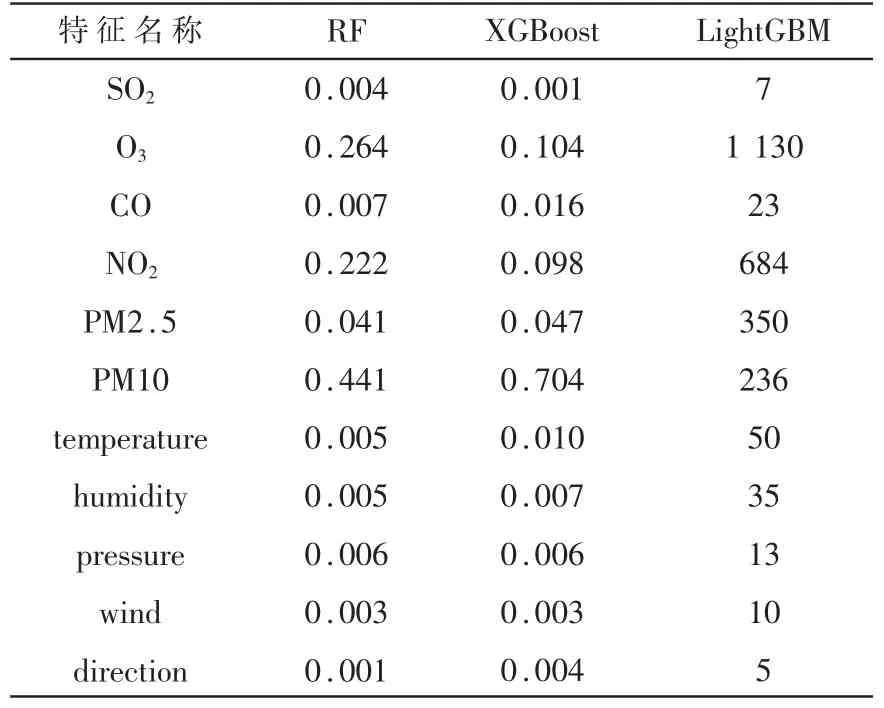
表2 特征重要性表

RF模型、XGBoost模型与LightGBM模型对数据集的所有特征进行重要性排序如图2、图3和图4所示。

图2为RF模型生成的特征重要性排序图，图3为XGBoost模型生成的特征重要性排序图，图4为LightGBM模型生成的特征重要性排序图，纵坐标为特征名称,横坐标为特征重要性值。分析图2、图3、图4 可知，三种模型对所有特征的重要性排序不尽相同，但是三种模型均是PM2.5、PM10、NO2、O3排在前四，因此可以认为PM2.5、PM10、NO2、O3是影响空气质量的主要因素。值得注意的是，RF模型的排序结果中direction(风向)与wind(风速)对空气质量影响最小，XGBoost模型的排序结果中是SO2与wind(风速)，而LightGBM模型认为是direction(风向)与SO2。为了提高数据的泛化能力以及模型的预测精度，本文选择PM2.5、PM10、NO2、O3、CO、SO2、temperature(温度)、direction(风向)、pressure(压强)、wind(风速)、humidity(湿度)作为特征。

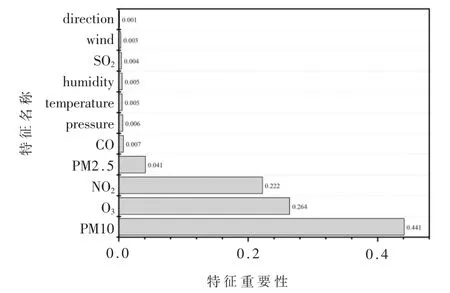
图2 RF模型特征重要性排序图

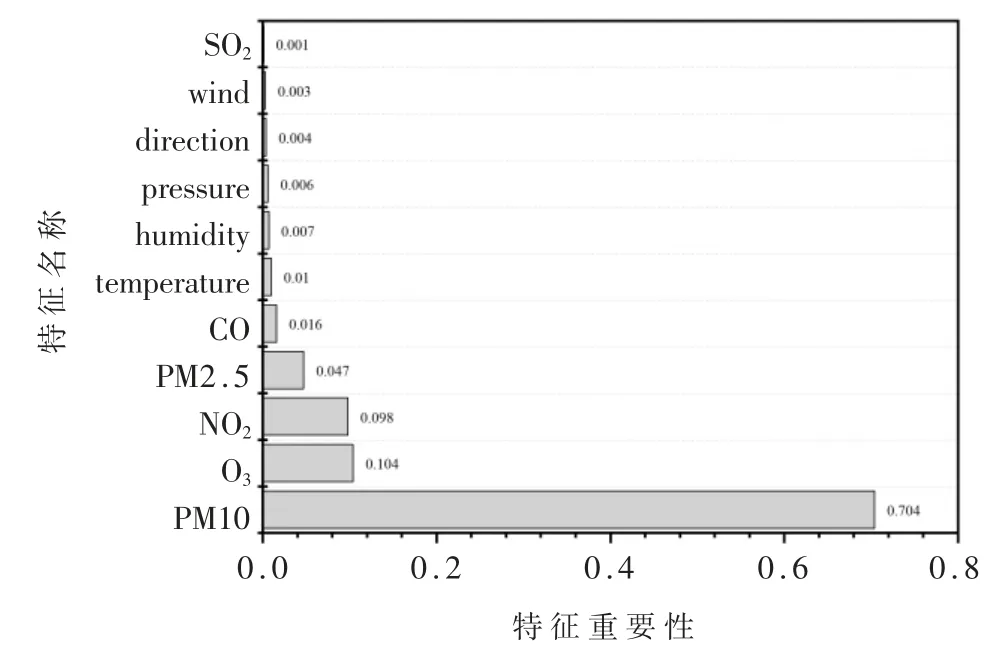
图3 XGBoost模型特征重要性排序图

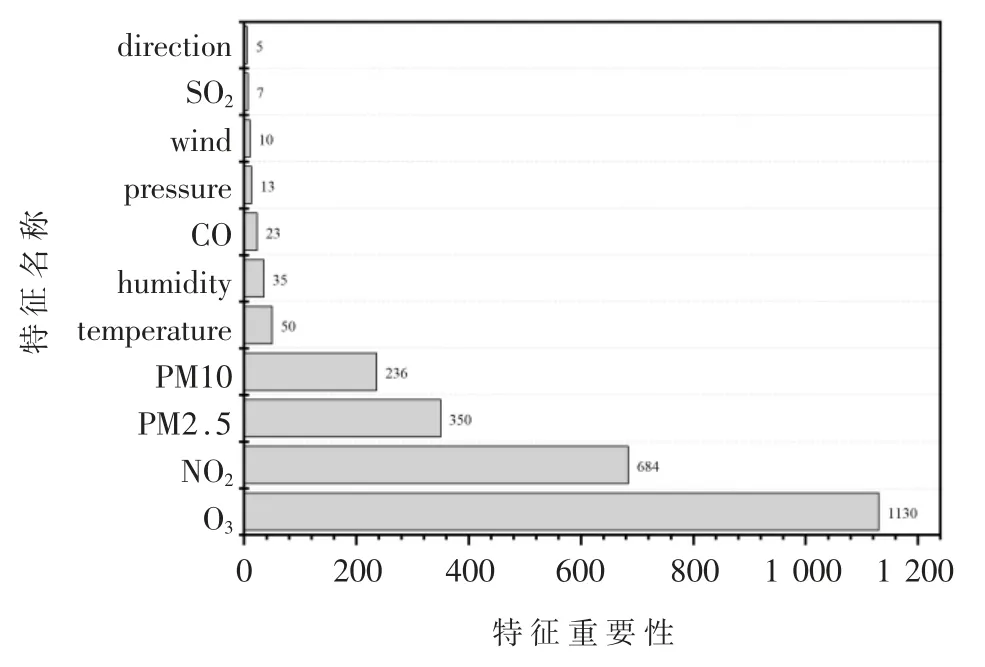
图4 LightGBM模型特征重要性排序图

2.3 实验测试

将选择好的特征以及实验数据按照训练集与测试集占比为7:3的比例划分，为了避免因每次数据集划分不同带来的误差，将前5 955条数据固定作为训练集，将剩余数据作为测试集送入到自适应Boosting模型进行训练，利用误差平方和倒数法等五种方法根据AdaBoost、XGBoost与LightGBM三个模型的表现自适应地分配权重，将三个模型的预测结果按照权重重构得到最终的预测结果。

3 实验结果

将数据送入模型中训练，AdaBoost、XGBoost与LightGBM三个单一模型以及五种权重计算方法下的组合模型的综合评价指标如表3所示。

由表3可以可知，在单一模型中，效果最好的是LightGBM模 型，MAE为8.108 7，RMSE为10.407 8，R2为0.849 6，三项指标均为单一模型中的最优。每种组合方法构造的自适应Boosting组合模型的RMSE与MAE均小于单一的模型，R2均大于单一模型。组合模型中精度最高的是采用误差平方和倒数法进 行 组 合，MAE为7.124 4，RMSE为9.367 1，R2为0.863 9，与单一模型相比，MAE平均减小了1.95，RMSE平均减小了2.26，R2平均提高了0.05，验证了自适应Boosting组合模型的有效性，同时也证明了自适应Boosting组合模型能提高空气质量预测精度。

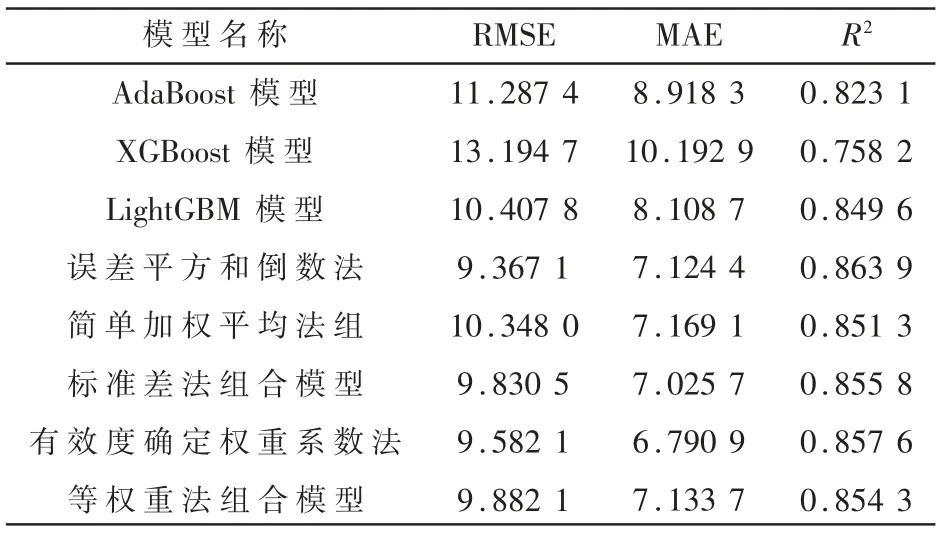
表3 模型综合指标对比表

将各种组合方法以及单一模型在2021年3月23日0：00至2021年3月23日23：00的AQI预 测曲线与真实值进行对比，如图5和图6所示。

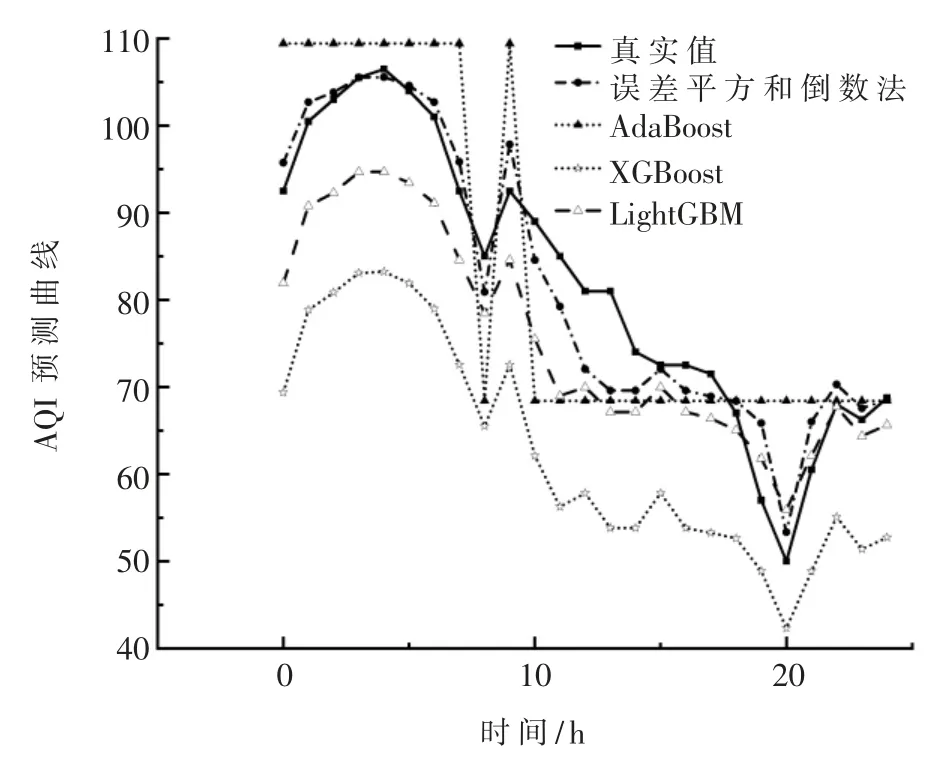
图5 单一模型预测曲线对比图

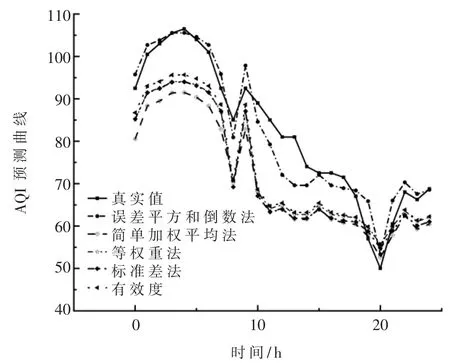
图6各种组合方法预测曲线对比图

图5 是三个单一Boosting模型、误差平方和倒数法组合模型与真实值的AQI曲线。分析图5可知，单一模型中LightGBM模型与XGBoost模型的预测值的走势与真实值基本一致但数值普遍偏低，AdaBoost模型的AQI预测值与真实值之间的误差最大。误差平方和倒数法组合模型的AQI预测曲线能准确地预测出AQI真实值的变化趋势并且预测值与真实值误差较小，综合表3和图5的结论，证明采用误差平方和倒数法进行自适应权重计算的组合模型预测效果优于单一的Boosting模型。

图6是五种权重计算方法的组合模型与真实值的AQI曲线。分析图6可知，每种权重计算法方法下的组合模型的预测值与真实值的趋势基本相同，但除误差平方和倒数法外的其他组合模型预测的AQI数值与真实值由较大偏差。误差平方和倒数法组合模型在大部分时间点上能精确地预测，对于相邻时间点AQI值剧烈变化的情况不易受到影响也能较好地适应，对峰值和谷值的预测存在着偏差但是并不影响AQI等级的划分，不会对空气质量预报产生较大影响。

4 结论

本文提出的自适应Boosting组合模型中，误差平方和倒数法组合模型在综合指标方面平均绝对误差、均方根误差以及决定系数均优于其他的组合模型和单一的Boosting模型，在与真实值的拟合程度方面曲线走势与真实值一致，预测的数值与真实值最为接近。从预测曲线可以看出，误差平方和倒数法组合模型对AQI的拟合效果最好，而且误差平方和倒数法组合模型不易受到相邻时间节点AQI值剧烈变化的影响。综上可以得出结论，自适应Boosting组合模型可以充分发挥单一Boosting模型的优势，提高预测精度。