顺层结构边坡稳定性一般性分析

王希宝, 袁 松, 黎良仆, 陈柯竹

(四川省交通勘察设计研究院有限公司， 四川 成都 610017)

0 引言

顺层岩质边坡是指坡体内的优势结构面与边坡具有相同倾向的层状岩质边坡。顺层岩质边坡破坏方式主要有：顺层滑动和溃屈破坏。顺层滑动是指前缘坡脚临空并具有明显、潜在的顺倾向滑动面而发生的整体失稳顺层下滑，这在顺层边坡开挖中经常出现。溃屈破坏是边坡前缘坡脚处受阻而发生的破坏形式，是顺层岩质高边坡的典型破坏模式。

顺层边坡滑动一般指顺沉积岩层面，有时也指顺岩浆岩或变质岩中倾向开挖坡面外的长大贯通的优势节理面，此类岩内部一般平整度较差，充填少。按沉积岩层面与自然山体交线出露位置，顺层岩质边坡可分为坡面出露型和坡背出露型两大类(见图1)，其边坡特征见表1。

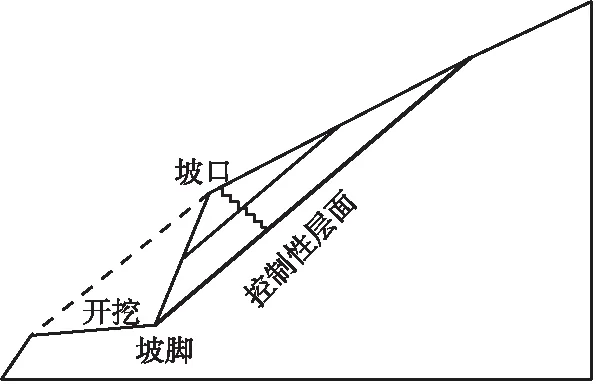
(a) 坡面出露型

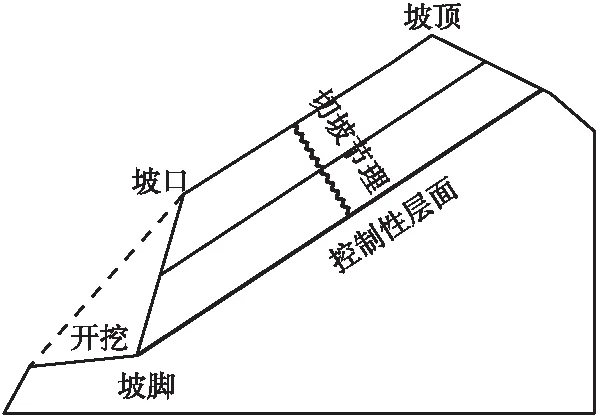
(b) 坡背出露型

表1 两种顺层边坡特征分类自然特征工程地质特征坡面出露型原始坡面坡角小于岩层倾角,岩层层面出露于地表地表水易于渗入坡背出露型原始坡面坡角大致与岩层倾角平行,大多数情况下坡面即为层面,表面见大面积基岩出露,植被稀少常见顺层滑动

工程实践中，顺层岩质边坡开挖后发生失稳破坏的情况很多[1]，具有滑移速度快、距离远、牵引式逐级滑动的特点，一旦启动后处治困难。顺层岩质边坡设计的难点在于如何确定滑移失稳的范围和层面抗剪强度[2]。关于滑移失稳范围的确定，行业内主要有3种意见，一是基于工程地质类比法取3～5倍开挖坡高，二是采用边坡变形监测确定影响范围，三是采用岩土数值法计算。方法一只考虑开挖坡高因素，简单易操作，但文献[3]模型试验结果表明影响范围受岩层倾角影响很大；方法二在勘察设计阶段无法应用；方法三对技术人员能力要求较高,存在较大的应用难度。文献[3]选择典型工点针对坡面出露型顺层岩质边坡开展的模型试验和数值分析表明，开挖变形影响范围沿层面长度与切层厚度之比为6.5～7.8，坡背出露型为4～6.5，该结论是根据典型工点研究得出，是否适用于一般情况还需要进一步研究。文献[4]建立了顺层边坡岩体失稳破坏长度的计算式，但理论性略强，不利于推广；文献[5]建议对于有裂缝未滑动的顺层边坡，防治范围取开挖深度的 2.0～3.0 倍，已变形滑动的则取为3.0～4.5倍，其具有一定参考价值，但过于笼统，且针对性不强。

本文以受沉积岩层面控制的顺层边坡为研究对象，根据前述2种顺层岩质边坡类型，采用极限平衡法分析讨论其稳定性计算方法与滑坡推力计算模型范围，推导得出了不同工况下稳定性计算公式，具有力学原理清晰、结构简单、便于使用的特点。

关于层面抗剪强度确定方法，除了传统的工程地质类比法、室内外试验法之外，文献[3]讨论了由结构面粗糙度确定其抗剪强度的方法，但现场操作较困难。本文进一步完善了采用纯摩试验获取结构参数的操作方法。

1 坡面出露型稳定性分析

1.1 受层面控制的顺层边坡

地层受构造作用不强烈、切层节理不发育、层面控制斜坡稳定性时，边坡稳定性受穿过坡脚的最不利层面控制。稳定性计算如式(1)所示，切层坡面见图2,其中α为边坡开挖坡角，β为斜坡坡角。

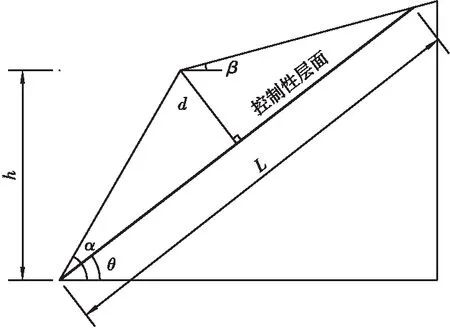
图2 切层坡面

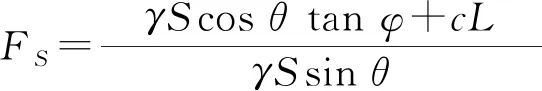
(1)

式中：FS为稳定性系数；γ为岩体重度；S为顺层滑动岩体面积，m2；θ为层面倾角(或视倾角)，°；c为层面内聚力，kPa；φ为层面内摩擦角，°；L为控制性层面长度，m。

假设由通过坡脚控制性层面切割的顺层滑动岩体为一理想三角形块体，通过三角形面积等效关系可将公式(1)整理成式(2)或式(3)。

(2)

(3)

式中：h为边坡开挖高度，m；d为顺层滑动岩体厚度，m。

据上述公式可见，受层面控制的坡面出露型简单顺层边坡稳定性系数只与边坡开挖高度或切层厚度这一几何参数有关，与坡口外自然斜坡倾向倾角无关，即无论坡口外自然斜坡是仰坡、平坡或下坡(见图3)，稳定性系数均相等。趋势上，该工况稳定性系数与开挖高度呈反比，开挖坡面越陡，稳定性越低。

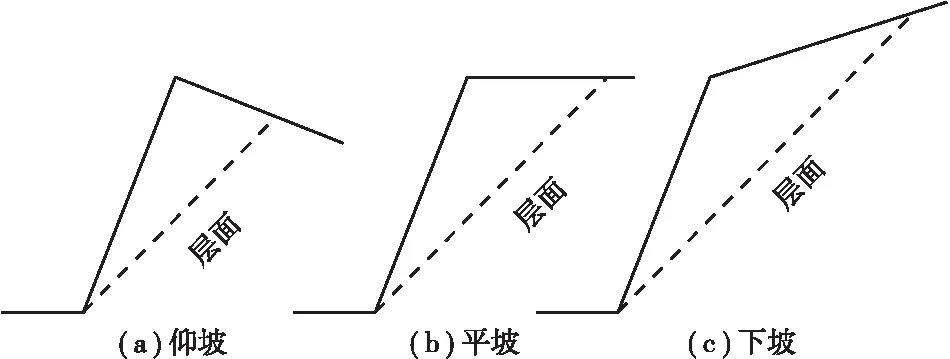
图3 不同斜坡坡面倾向

根据上述分析，可以得到两个有益的结论：

1) 层面抗剪强度包含黏聚力贡献时，稳定性随开挖坡高增大而降低，以无黏聚力稳定值为渐近值。工程设计时可通过降低坡高提高边坡稳定性达到设计规范要求。层面内聚力对水敏感时，宜采取有效措施防止控制性层面浸水。

2) 不规则坡体稳定性计算。按照体积(面积)等效的原则，将不规则自然坡面等效(BA′∥CA)为开挖坡高为h′的标准三角形后，即可根据式(3)计算稳定性(见图4)。采用该方法也可用于快速分析和比较同类边坡稳定性。

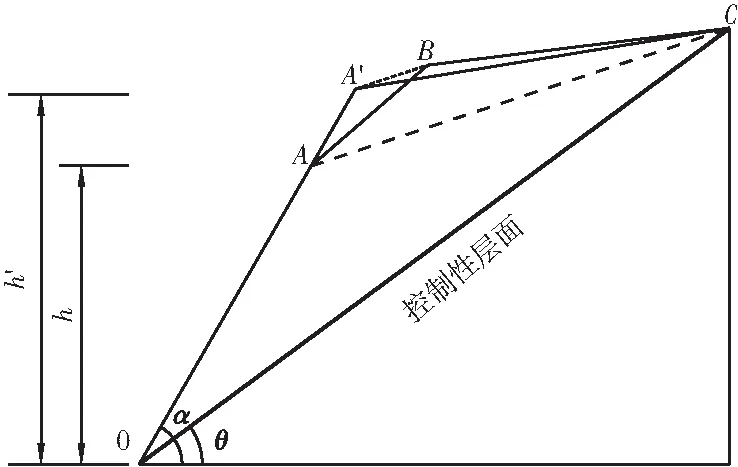
图4 不规则坡面的等效计算示意

1.2 受切层节理(共轭X节理)控制的顺层边坡

共轭节理(Conjugate joints)是指岩石受剪切应力破裂形成的裂隙，属于剪切节理的一种。理论上应变椭球体的两组最大剪切面的夹角为90°，在两组剪切面上同时发育两组剪切节理，称为共轭节理。沉积岩受单向压力作用时，易形成一组显著优势的垂直于层面的共轭节理。受节理控制的切层型顺层坡面具有不一样的性质(见图5)。

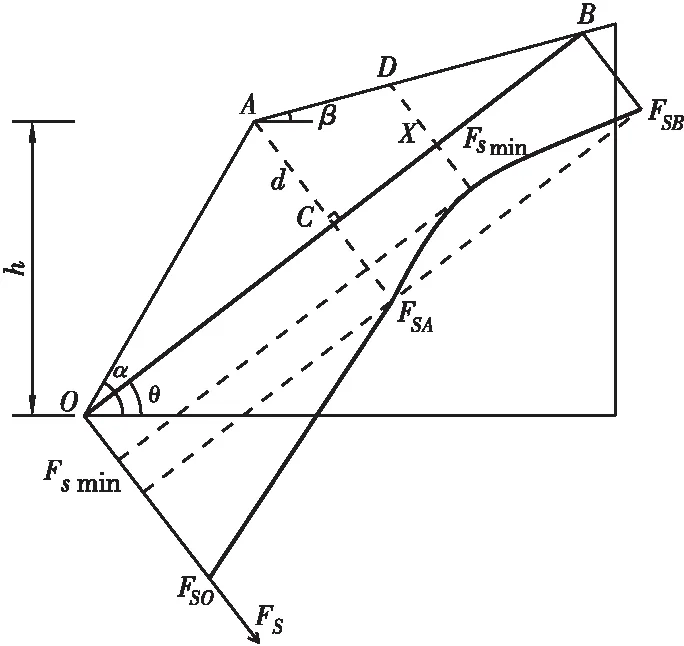
图5 受层面和切层节理控制的边坡稳定性系数

如图5所示，三角形OAB为通过坡脚的控制性层面与开挖坡面、自然斜坡构成的滑动岩体。根据前述结论，OAB与OAC的稳定性相同，以层面为x轴，O点到C点的稳定性呈线性降低。根据图4的等效原理，四边形OXDA稳定性小于OAB和OAC，即稳定性最小值位于CB段某处。设该处距离点C距离x[x≤dcot(θ-β)]，推导出四边形OXDA稳定性计算式为：

FS=cotθtanφ+

(4)

对上式求极值，可得稳定性系数最低位置并计算稳定性，也可采用Excel试算法或CAD作图法确定最不利切层节理(拉裂缝)位置。

作图法具体做法：设任意X点位置，DX为切层节理，过D点做XA的平行线与OA的延长线交于点E，如前所述，因OXDA的面积与OXEA相等，则根据OE的垂高可计算得到OXDA的稳定性系数。自CB连线方向依次作图，可逼近得到位置最高的E点，即为稳定性最低的裂缝位置(见图6)。

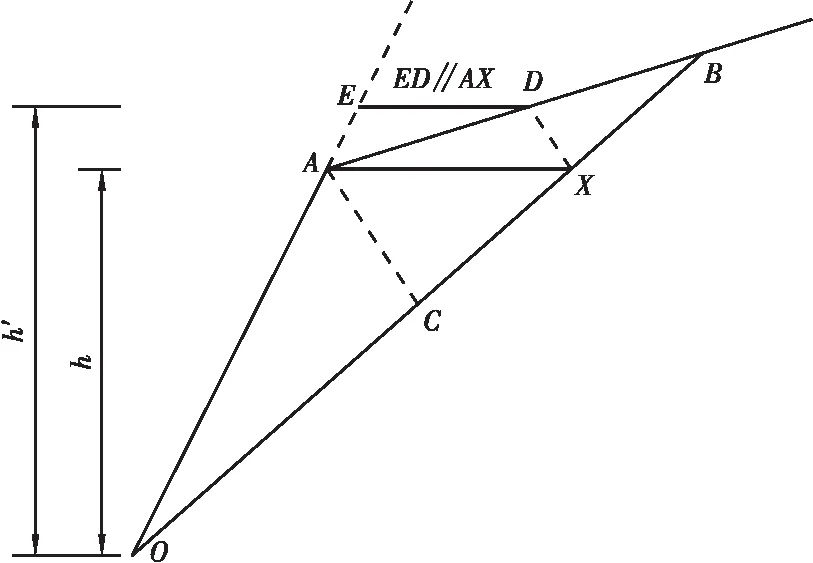
图6 作图法确定稳定性最不利拉裂缝位置

2 坡背出露型稳定性分析

选取自然坡面与层面平行的特殊情况，分析因坡脚开挖导致的顺层边坡稳定性。

2.1 天然工况

岩层发育切层节理裂隙情况，以最外缘节理裂隙为后缘情况(见图7)，顺层边坡稳定性系数见式(5)。随后缘切层节理裂隙距坡口越远，切割顺层岩体稳定性越低。对节理裂隙距坡口距离x求极限，可得此类边坡稳定性系数极小值如式(6)、(7)所示，其值与开挖切层厚度d或开挖坡高h呈反比。若计算极值小于1.0，则边坡将发生失稳。理论上，其失稳后缘可以发生在极限平衡(FS=1.0)点以上任意位置。

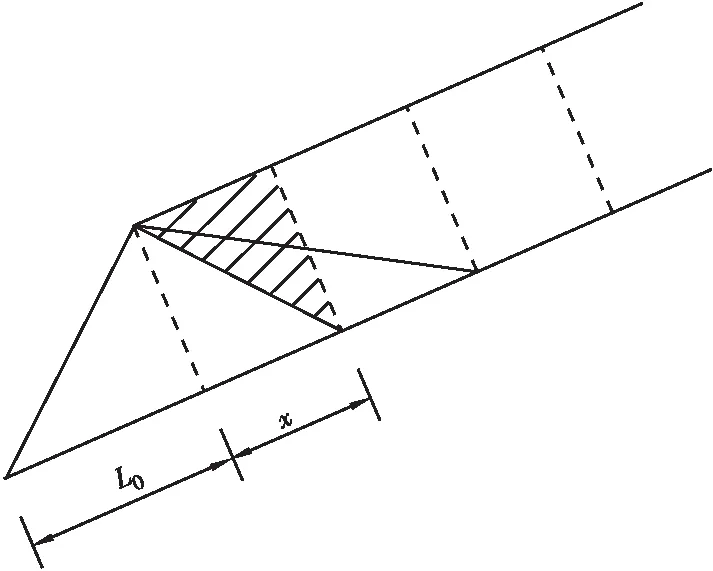
图7 等厚顺层坡面

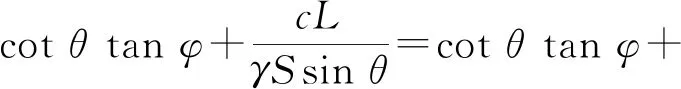
(5)

随边坡高度增加，稳定性系数降低，求极限(x→∞)可得最小值:

(6)

或

(7)

某符合图7构造特征的顺层岩质边坡典型算例，不同距离x处的的稳定性系数和设计工况下的剩余下滑力(不考虑降雨与地下水)如图8所示，随距离增加,稳定性逐渐降低并趋近于极小值，降低幅度前大后小，但剩余下滑力基本呈线性增加。从设计角度，以远距离节理裂隙作为后缘边界进行支挡设计没有必要,也是极其浪费的[6～7]。可以FS=1.0位置计算剩余下滑力作为支挡结构设计依据。

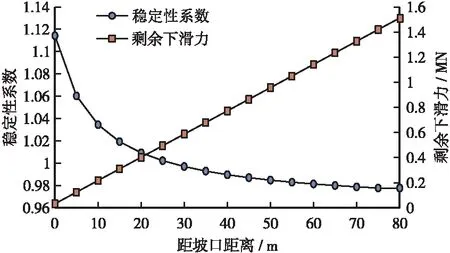
图8 稳定性系数、剩余下滑力与拉裂隙位置关系

2.2 降雨(裂隙充水)工况

降雨时，坡面地表径流自上而下渗入并充填节理裂隙，根据裂隙发育情况分为单裂隙和多裂隙。实际上单裂隙充水是多裂隙充水的特殊情况。

2.2.1单裂隙充水

单裂隙充水工况见图9,图中dh为裂隙静水压力高度。

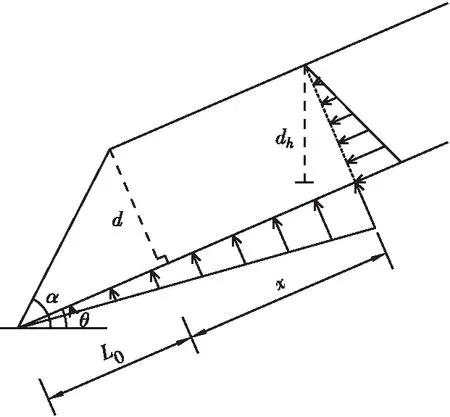
图9 单裂隙充水时滑体受静水压力

岩体同时承受拉裂隙静水压力和扬压力，则有稳定性系数FS：

(8)

式中：γw为水重度。

求极限(x→∞)，得

(9)

2.2.2多裂隙充水

多裂隙充水工况见图10。

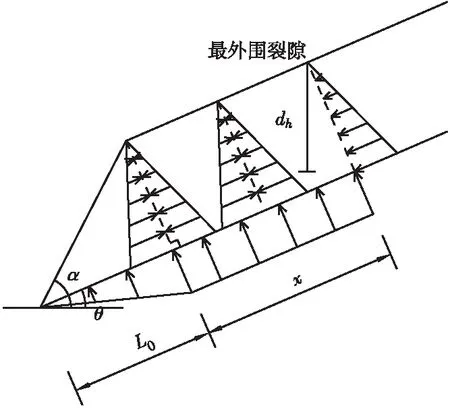
图10 多裂隙充水时滑体受静水压力

假设所有裂隙均完全充水，顺滑面方向静水压力除最外围裂隙处均为内力(上下抵消，不影响滑体整体受力)，则有稳定性系数FS：

(10)

求极限(X→∞)，得

(11)

一般在连续降雨工况下，构造切层裂隙极易充水，多裂隙充水是最不利情况。同样的，在进行该类顺层边坡处治设计时，也可以FS=1.0位置计算剩余下滑力作为支挡结构设计依据。

3 结构面参数确定

3.1 工程类比

类比分为类比规范查表法和现场同类型边坡类比法两种。前者是根据调查获得的层面发育特征，查规范表获得剪切强度；后者是根据现场调绘同类型自然边坡，反算获得抗剪强度。一般情况下，查表法准确度取决于设计人员的经验，偏差较大；而调绘类比法因假设自然斜坡稳定性系数较低，故反算参数一般偏低，容易造成工程浪费。

3.2 现场大型剪切试验[8]

现场大型剪切试验直接针对目标岩体岩层面构筑试验条件，因此较室内试验更能符合岩土体天然状态，得出的结果更加符合实际工程，但存在试验制样复杂，时间长、耗费高的特点。

3.3 纯摩试验

为了快速获得岩体节理特别是层面的抗剪强度，可以采用现场纯摩试验。试验具体操作方法和步骤如下。

1) 取样与制样：人工开挖切层取样，试样包含的结构面尺寸不小于30 cm×30 cm或同等面积，务必确保结构面接触状态不改变，结构面充填物不流失。

2) 搭建场地平台：搭建或选择一水平场地，准备试样底板(木板或铁板，带边棱，带固定测角装置，比如罗盘)。

3) 试验：记录将试样固定于底板上，以不大于0.5(°)/s的速度缓慢抬起底板，至上岩块滑动，记录倾斜角度。在上岩块绑缚重物(重物质量以上岩块质量1/3～1/2为宜)，上下岩块接触面原样重置后再次试验，记录倾斜角度。该岩块试验结束，称重上岩块重量与绑缚重物重量，米格纸描出结构面面积。

解联立方程组可获得每个剪切岩样的结构面黏聚力和内摩擦角，每组试验不少于3个岩样，取3组试验参数平均值作为结构面抗剪强度参数。

3.4 根据已滑坡边坡边界条件反算

根据地质调绘测量确定的地面线、滑动面特征要素、剪出口与首次滑动的后缘位置，可基于2个独立坡面建立稳定性计算方程，求解抗剪强度。

4 结语

1)受层面控制的坡面出露型简单顺层边坡，其稳定性与边坡开挖高度呈反比关系，以无黏聚力稳定值(cotθtanφ)为渐近值。

2)受层面与切层节理共同控制的坡面出露型顺层边坡，稳定性系数曲线以坡口与过坡脚层面的垂线交点为界，前段为线性下降，后段为凹曲线。导致边坡稳定性最不利的切层拉裂隙位置位于开挖坡口与过坡脚层面与自然斜坡交线之间，可通过求极值、试算或作图法确定。

3)坡背出露型顺层边坡，稳定性随自然斜坡坡高增加而降低，计算剩余下滑力选择的模型范围宜选择稳定性系数等于零的位置作为上边界。