往复压缩机出入口压力变化对级间压力的影响分析与模拟
2023-01-15梁华,陈超,徐辉
梁 华,陈 超,徐 辉
(1. 中国石化工程建设有限公司,北京 100101; 2. 山东裕龙石化有限公司,山东 烟台 256716)
往复压缩机作为最常用的气体增压设备,适用于中小流量、高压比的工况,广泛应用于炼化企业【1】。
往复压缩机在设计时往往按照特定的工况设计,而实际运行过程中,压缩机出、入口的压力往往是波动的,从而导致级间压力的重新分配。对于已有的压缩机,主要的结构尺寸是已知的,但是由于工艺流程等原因,进气压力、排气压力或容积流量发生了变化,这就需要重新计算其级间压力以及该压力下的其他参数,用以判断压缩机能否满足新的使用条件下的工况,这种复算称为压缩机的热力性复算【2】。
1 压缩机热力性复算
热力性复算需要知道压缩机的基本参数,如压缩机的每一级的缸径,行程,活塞杆直径,余隙容积,压缩机每一级的入口温度,压缩机的出、入口压力,以及压缩机的压力系数、温度系数、泄漏系数、析水系数、净化系数等参数。

表1 三级压缩的纯氢气压缩机相关参数
为简化计算,认为气体为理想气体,级间的冷却、分离及相关管路没有压降,前一级的出口压力就是下一级的入口压力。
初步计算入口压力变化前的吸气量如下(所有流量均换算到第一级入口状态):
V1=λP1λT1λL1λφ1λC1λV1Vh1
(1)
(2)
(3)
V1=V2=V3
(4)
式中:V1、V2、V3——分别代表一个往复行程下第一级~第三级气缸的吸气量,m3。
如果此时入口压力突然变成1.5 MPa(绝),而其他参数不发生变化,那么此时的级间压力就会重新分配。重新分配的要点就是:找到级间的压力分配,让新工况下的压缩机各级的吸气量保持平衡,即新工况下的吸气量V1′=V2′=V3′(均换算到第一级入口状态)。
为方便分析,假设新工况下的压缩机仍然按照等压比分配,每级压比约为2.2,则每级的压力如表2所示。

表2 新工况等压比下的压力分配
此时,新工况下的综合系数Kj′、相对余隙容积αj′、膨胀指数mj′可认为近似等于入口压力未变化前的数值,且行程容积Vhj没有变化,则此时每级的吸气量如下(均换算到第一级入口状态):
2.1 3组人群血清HE4、CA125表达水平及ROMA指数比较 3组人群血清HE4、CA125水平和ROMA指数均呈非正态分布,卵巢癌组人群血清HE4、CA125水平和ROMA指数的中位数分别为88.05 pmol/L、51.85 U/mL和31.17%,均高于卵巢良性肿瘤组和健康对照组的血清水平,差异具有统计学意义(P<0.05)。卵巢良性肿瘤组与健康对照组比较,血清CA125水平差异具有统计学意义(P<0.05),两组间HE4水平和ROMA指数比较,差异无统计学意义(P>0.05)。见表1。
(5)
(6)
(7)
由此可以看出,要想使V1′、V2′和V3′相等,必然要使得第一级压比ε1′在2~2.2之间、第二级压比ε2′在2.2附近、而第三级压比ε3′>2.2。
因此可以得出结论,即当入口压力变小(或出口压力变大)而其他参数不变的情况下,每级压比都会增加,第一级压比增加比例最小,后几级压比增加比例逐渐增大,且最末级压比增加的比例最大。
反之也可以得到相似的结论,即入口压力变大(或出口压力变小)而其他参数不变的情况下,每级的压比都会减小,且最末级的压比减小的比例最大。
事实上,真实的往复压缩机的热力性复算是比较复杂的,如式(1)~式(4)中,有6个未知数,6个方程,理论上可以求得级间的压力分配。但是,这些公式中的各个参数相互关联,直接求解往往比较困难,实际复算时经常要用试算迭代的方法进行求解。
2 出、入口压力变化时的HYSYS模拟
如前所述,压缩机的热力复算较为复杂,即使借助编程也存在不少弊端。主要是:1)很难解决实时变化的压缩系数;2)很难解决实时变化的过程指数;3)难以解决级间的大分子量或水蒸气的凝液析出;4)无法计算平衡破坏后,再次实现平衡的时间。而HYSYS的往复压缩机的动态模拟,完美地解决了以上问题。
以1台4M16的CO2压缩机为例,其主要参数如表3所示。
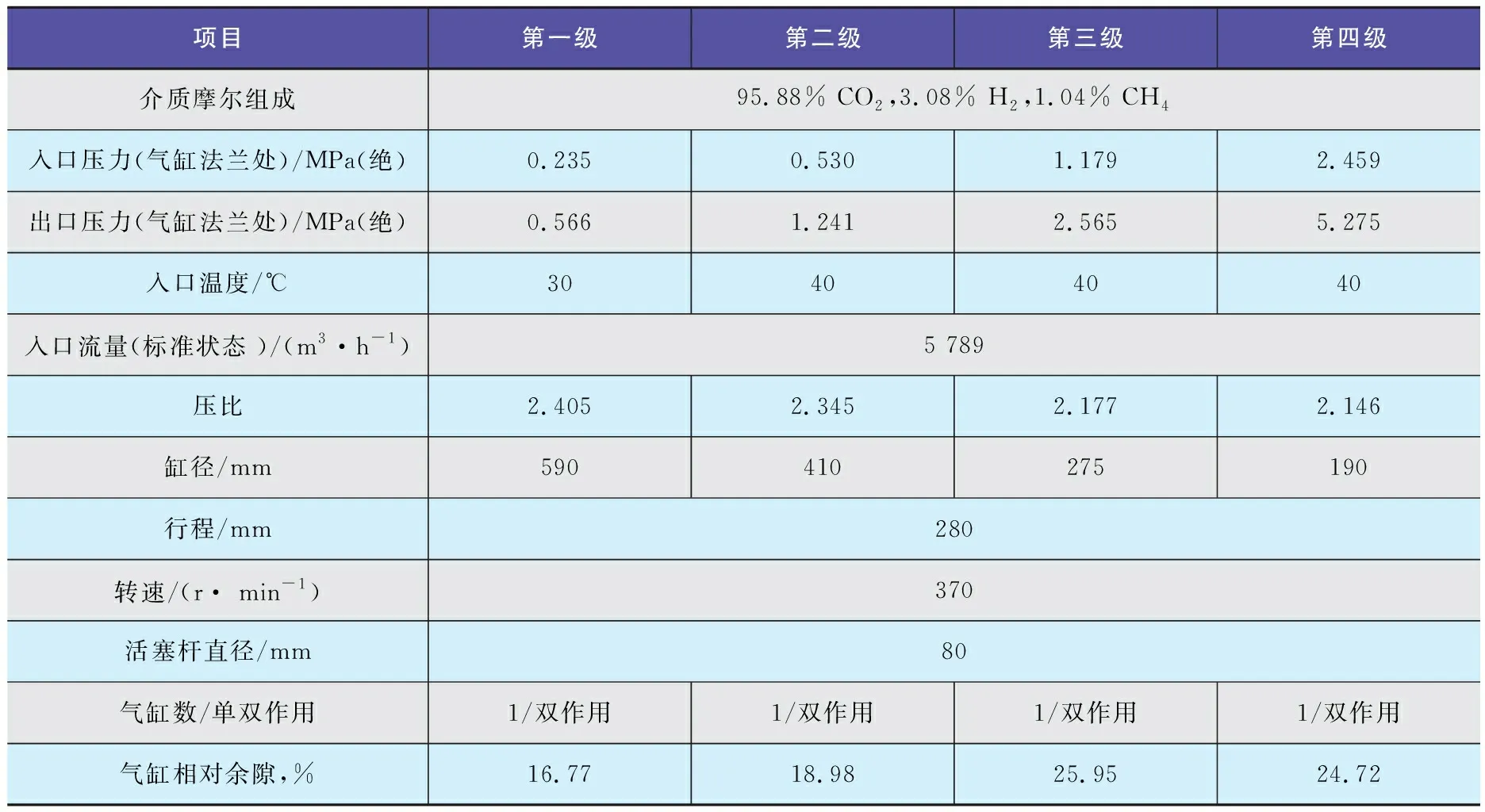
表3 4M16CO2压缩机的主要参数
先将物料信息输入到HYSYS中,选择常用的Lee-Kesler物性方法,并建立HYSYS模型,如图1所示。
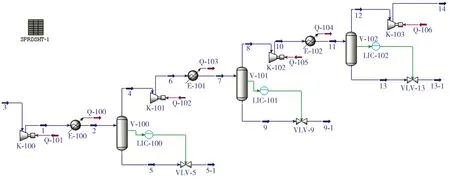
图1 HYSYS模型
将表3参数输入到HYSYS当中,HYSYS会自动计算每一级的压缩系数、过程指数以及是否有液相析出等。
为方便监测各出、入口压力变化以及各级压比的变化率,一方面设置曲线监测,另一方面将重要的结果输出到电子表格中。初始状态下的压缩机参数如图2所示。

图2 初始状态下的压缩机参数
压缩机运行一段时间后,将入口压力从235 kPa降低到180 kPa,再次平衡后的压缩机参数如图3所示。
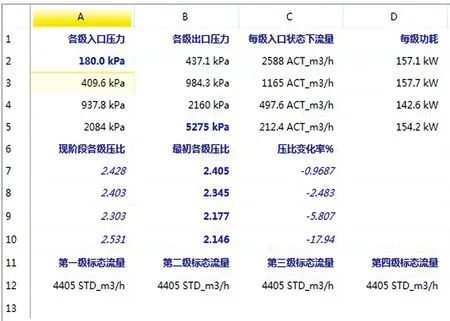
图3 再次平衡后的压缩机参数
从图3中可以看出,相对于初始状态,各级压比均有所上升,且第四级压比上升得最多,达到17.94%,验证了第1节中的结论。
这就要求在压缩机设计时,应充分考虑压缩机出、入口的压力变化情况,尤其是入口压力变小(或出口压力增大)的工况,以防止压缩机机械损坏或超温停车,且应着重校核末级气缸组件的可靠性。
图4是各级压比的变化情况。从图4中可以看出,变化的初始(图4中3 000 s的位置),第一级的压比突然改变为565.3/180=3.14,其他级压比不变,随着压缩机的运行,第一级压比迅速下降,而各级压力都经历了先上升后下降到均衡位置的一个过程。存在上升过程是由于级间罐的滞留效应引起的。

图4 各级压比的变化情况
虽然现实中的压力大都是缓慢波动的,但对于存在压缩机入口压力瞬间变小(或出口压力瞬间提高)工况的情况,仍应考虑机组的瞬时破坏和瞬时超温。
由图4可知,该机组从压力突然变为180 kPa开始,大约经过100 s系统即达到了再次平衡。
出口压力增大工况下的模拟结论与之前描述一致,在此不再赘述。
3 结语
多级往复压缩机出、入口压力波动时,往往最后一级的压比波动最大,这就要求压缩机在设计或校核时,应充分考虑出、入口压力波动带来的各级压比的波动,并校核波动时的机组可靠性。
HYSYS作为比较先进的模拟计算工具,可以快速准确地计算出、入口压力波动时的级间压力分配,并可模拟平衡过程和平衡时间,是非常实用且有效的模拟工具。
