考虑应变率效应的混凝土随机损伤本构模型研究1)

虢成功 李杰

(同济大学土木工程学院,上海 200092)

引言

混凝土材料是土木工程应用最广泛的建筑材料.但由于混凝土材料的高度复杂性,一些关键的科学问题尚未得到完善解决,混凝土材料的受力本构关系即是其中之一[1].

在受力过程中,混凝土材料表现出复杂的非线性力学行为,如刚度退化、强度软化、单边效应、卸载后存在不可恢复变形等[2-3].同时,由于多相介质材料的随机分布及各相材料自身力学性质的随机性,混凝土的受力力学行为具有不可避免的随机性[4-5].试验表明:随着加载速率的增加,混凝土材料强度会有不同程度的提升,相较静力作用,动力作用下的裂纹形态往往出现分岔、弥散分布的特点[6-8].非线性、随机性和应变率效应,构成了混凝土材料受力力学行为的三大基本特征[1].

损伤力学的出现与发展,为科学反映混凝土受力力学性质提供了基础[9].从20世纪80年代开始,经过如文献[10-14]等一批代表性学者的创造性工作,已经形成了确定性的损伤力学基本理论[15-18],为混凝土结构的非线性受力力学行为分析提供了科学基础.21 世纪初以来,李杰等[19-24]引入随机介质的基本概念,逐步建立了混凝土随机损伤力学的基本理论.在这一研究中,将混凝土材料中的骨料、砂浆、界面过渡区等视为随机介质,用随机介质假定替代经典连续介质力学中的均匀性假定,从而打破了混凝土多相复合介质材料中的“相”概念,实现了单一的综合介质材料的随机描述.基于随机介质和随机损伤的观点,从混凝土的微-细观缺陷入手,发展了微-细观随机断裂模型[19-22],为科学反映混凝土受力力学行为的非线性与随机性提供了基础.然而,无论是确定性损伤力学[25-28],还是随机损伤力学[29-30],对混凝土材料的应变率效应问题,均没有提供完整的解决方案.

鉴于上述背景,本文试图通过新的努力,基于速率过程理论分析混凝土代表性体积元RVE 受力过程中的能量耗散关系,通过假定裂纹间的相互作用与应变率相关,在微-细观随机断裂模型的基础上建立适用于中低应变率范围的随机损伤本构模型,以期为混凝土结构的动力非线性分析提供基础.

1 连续弹塑性损伤力学框架

弹塑性损伤本构模型可以表述为[1]

式中,σ,ε和εp分别为应力张量、应变张量和塑性应变张量;I,D和E0分别为4 阶单位张量、损伤张量和弹性刚度张量.

借助应变等效假定[31],可以将损伤和塑性解耦

针对混凝土受拉和受压的差异,将有效应力进行谱分解

式中,σi和n(i) 分别是有效应力张量的第i个特征值和对应的特征向量,H为Heaviside 函数.

同时,将损伤分为受拉损伤d+和受剪损伤d-两个部分,可将损伤张量表示为损伤标量与对应投影算子的乘积之和

为了描述损伤演化这一不可逆的能量耗散过程,引入材料的Helmholtz 自由能Ψ

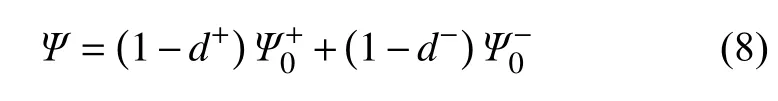
损伤能释放率Y±为Helmholtz 自由能关于损伤的对偶量

Wu等[14]基于Drucker-Prager 型势函数建立了的解析表达形式,并由此得到了损伤能释放率的显式表达

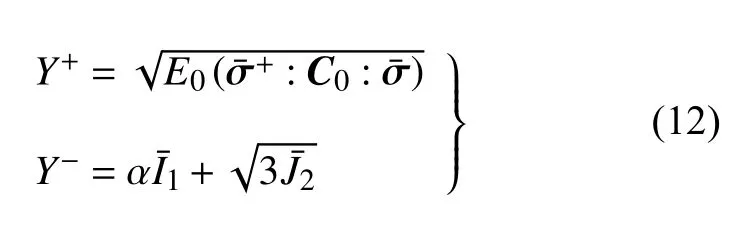
式中,E0为弹性模量,C0为4 阶柔度张量,和分别为有效应力张量的第一和第二不变量.

利用损伤能释放率建立的损伤准则具有热力学基础,损伤演化过程可以表述为损伤能释放率的函数

2 微-细观随机断裂模型

在上述确定性损伤力学的理论中,对于式(13)中的损伤演化函数G往往采用理性猜测或经验推广方式确定.这形成了确定性损伤力学理论中最大的缺陷.与之不同,随机损伤力学引入随机介质的概念反映非均质介质,开辟了综合反映混凝土受力力学行为非线性与随机性的科学道路.

从微观断裂的抽象物理模型出发,文献[19-22]逐步建立了基于抽象物理模型的随机损伤演化法则,形成了微-细观随机断裂模型.这一模型为综合反映准脆性材料的非线性与随机性打开了方便之门[1].

如图1 所示,将代表性体积单元抽象成微-细观并联弹簧模型.在该模型中,裂纹的产生、扩展和损伤的发展用微弹簧的随机断裂来表示.且每个微弹簧的应力-应变曲线假定服从弹-脆性关系.依据随机介质假定[1,23-24],随机损伤演化可表示为

图1 受拉微-细观随机断裂模型Fig.1 Tensile micro-meso stochastic fracture model

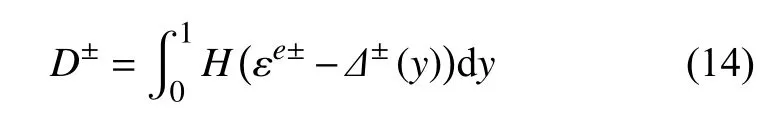
式中,H为Heaviside 函数; εe±为弹性应变,Δ±(y)为微弹簧断裂应变,可以假定为平稳随机场,其一维概率密度函数服从对数正态分布;y表示微弹簧的空间坐标.

令Z±(y)=lnΔ±(y),其均值为λ±,标准差为ζ±,则 λ±,ζ±与Δ±(y) 的均值和标准差满足如下换算关系

随机场Δ±(y) 的相关结构可以用指数型相关函数描述

式中,ω±为相关尺度参数,ϑ=|y1-y2|.

利用大量试验数据,文献[32]识别给出了不同等级混凝土对应的具体分布参数.结合概率密度演化理论[33],可以分析计算在给定应变时的应力概率密度演化过程[34].

3 纳-微-细观随机断裂模型

在上述微-细观随机断裂模型中,假定了微弹簧的应力-应变关系服从线弹性-断裂关系,即在微弹簧断裂前,不存在能量耗散,这并不符合真实的物理过程.事实上,关于微弹簧断裂物理的研究表明[35-36],在微观单元断裂前,存在不同尺度的能量耗散过程.

3.1 损伤发展的多尺度能量耗散

以单轴受拉为例,考虑微-细观随机断裂模型中的一个微弹簧单元.显然,微观单元内部存在更为细小的次级耗能单元.为此,首先考虑纳观尺度下一各向同性扩展的理想圆盘状裂纹(图2).由线弹性断裂力学可知,在加载过程中,纳观裂纹扩展单位距离δa的耗能ΔQ为[37-38]

图2 理想圆盘状裂纹Fig.2 Ideal planar crack

式中,ηa=2πra,Ga为纳观尺度的能量释放率.

假定存在与 δa相对应的损伤增量 δd,在这个过程中的能量耗散为[35]

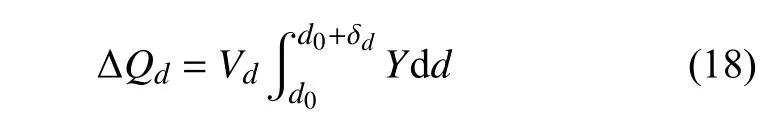
式中,Vd为损伤体积.

由于式(17)和式(18)描述的是同一个过程,显然有

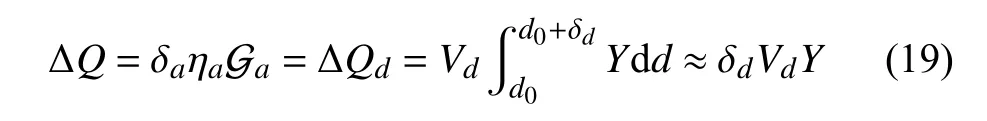
裂纹的扩展速率a˙ 记为单位扩展距离 δa和净能量势垒跨越频率f的乘积

如图3 所示,f可由速率过程理论[39]给出

图3 能量势垒跨越过程Fig.3 Energy barrier crossing process

式中,kB为Boltzmann 常数,h为Planck 常数,T为绝对温度,Q0为势垒高度.

速率过程理论适用的条件之一为ΔQ≫kT,所以可以对式(21)的双曲函数线性化.

设微观单元中各个尺度的裂纹分布可以用层级模型(图4)描述,且各尺度裂纹存在自相似特性,则纳观裂纹总数N可以表示为[35,38]

图4 裂纹层级模型Fig.4 Crack hierarchy model

式中,s表示从纳观到微观的裂纹层级数,ni表示第i个层级中的裂纹数量.

在不同尺度上,裂纹数量应该是裂纹驱动力的函数.在损伤力学框架内,裂纹驱动力即损伤能释放率Y

据此,文献[35]从函数 F 具有尺度不变性出发,推出其具体形式为幂函数

式中,qi为第i个尺度的分形参数.由此,裂纹总数N可以表示为

事实上,由于材料力学性能、缺陷和孔隙的随机分布,在外部作用下,准脆性材料的断裂在高应力区首先出现.随着载荷的增加,在已有的裂纹之间形成新的裂纹.而由于应力重分布,已有的裂纹也可能会发生闭合.当裂纹区域开始汇聚并形成局部化效应时,不同尺度的裂纹贯通、形成上一层级的裂纹.为考虑不同尺度裂纹之间的相互作用,可引入有效裂纹数Neff

式中,κ为表示应力屏蔽效应强弱的参数.

忽略纳米层级裂纹个体差异性,微观单元总能量耗散率可以用统计平均方法获得

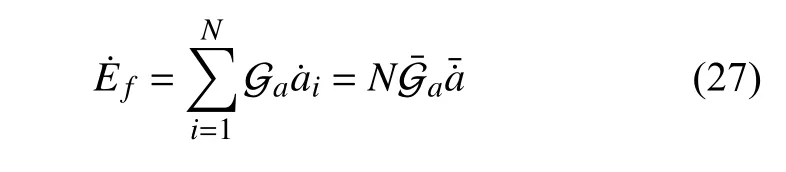
结合式(19)、式(20)和式(25),可求得微观单元总能量耗散率表达为

注意到损伤能释放率与应变之间的关系,结合式(28)可以发现微观单元的耗能与加载应变之间具有高度非线性关系.

3.2 随机损伤表达

将上述分析结果与微-细观随机断裂模型相结合,可以建立混凝土代表性体积单元的随机弹塑性损伤本构关系为

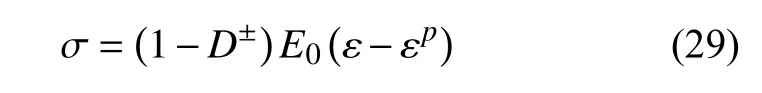
其中,随机损伤演化法则为

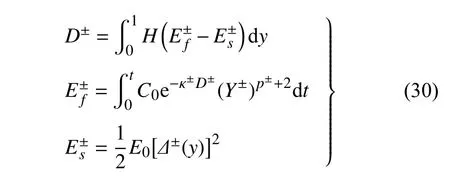
由此,便给出了可以反映混凝土多尺度损伤演化的纳-微-细观随机断裂模型.

借助应变等效假定,可以实现损伤子空间和有效应力子空间的解耦.由此,可以在有效应力空间引入塑性势函数,选用合适的流动法则计算塑性内变量的演化.为了避免在塑性子空间和损伤子空间迭代导致计算量过大的情况,也可以引入经验塑性模型[29,40]以适当简化计算,经验塑性模型一般表述为

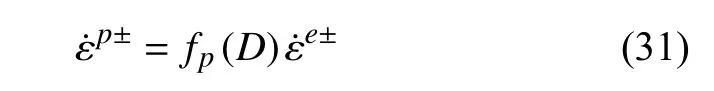
通常可选用文献[40]提出的经验塑性函数形式

3.3 考虑率效应的动力扩展

事实上,速率过程理论可以提供混凝土材料在不同加载速率下力学行为变化的解释.该理论认为材料的破坏问题可以视为粒子从亚稳态的逃逸问题:少数位于势阱底部的粒子通过热激活后跨越一个与外力和温度有关的能量势垒,从而对应粒子间键的破坏.在动力荷载作用下,强度的提高源自加载速率和原子键断裂速率的竞争机制[41-43].

以文献[41]经粗粒化处理后提出的倒N 型势为例(图5),求解不同加载速率下键的断裂速率.图中U为势能,δ表示原子键拉伸长度,k为键的刚度,A为初始无外力作用下的势垒高度,Eb为有效势垒高度,x表示反应坐标,当x=0时表示原子键完好,x=1 时完全断裂.

图5 倒N 型势垒Fig.5 Inverse N potential

势能U记为

键之间的力为

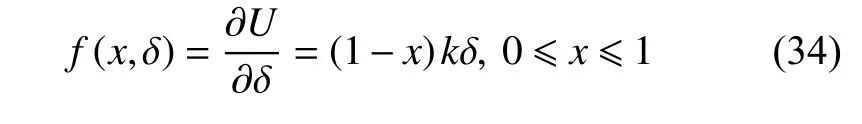
有效势垒高度为

当有效势垒为Eb=0时,可以求得临界伸长量δc=

假定x随时间的演化由Langevin 方程控制[41]

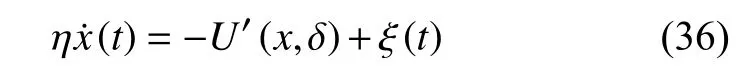
式中,η为黏性系数,U′(x,δ) 表示势能对反应坐标的导数,ξ(t)为随机力,通常可以假定为白噪声,其前二阶统计特征满足

式中,δD为Dirac 函数.

由于随机力的存在,需要求解x的概率密度函数p(x,t)随时间的演化.这一演化服从如下的Fokker-Planck-Kolmogorov(FPK)方程

由反应坐标x的物理意义可知:x=0处为反射边界,x=1处为吸收边界.

定义F(t)为被边界吸收的概率密度函数

显然,F(t) 的物理意义对应t时刻键断裂的概率.

利用特征值展开近似求解F(t).为此,对式(39)左右两边关于时间求导可得

将式(40)中概率密度函数关于时间的偏导数用一阶特征值近似[41,44]

式中,rx为该势垒形式对应的跨越频率.

将式(41)代入式(40),化简得到

跨越频率可以通过计算平均首次穿越时间(mean first passage time)获得[39].对于图5 的势垒形式

由此,跨越频率

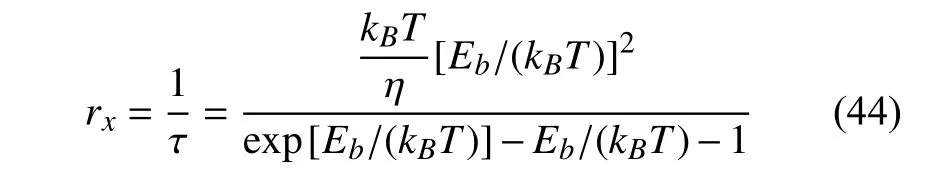
对式(33)、式(35)和式(44)进行无量纲化,得到

从图6 可以看出:随着加载速率的增大,F的演化变慢.由此表明,在同等拉伸长度下,加载速率高的键断裂概率小.显然,由于加载速率和键断裂速率存在竞争机制,在不同加载速率条件下,不同尺度裂纹的发展速度和闭合速度也是不一样的.依据这一分析,加载速率越高、裂纹扩展越慢,由此导致能量耗散相对减少,从而使得材料强度得到提高.进一步,依据相关试验[45-46],可假设式(26)中反映应力屏蔽效应强弱的参数 κ 与相对应变率的对数线性相关

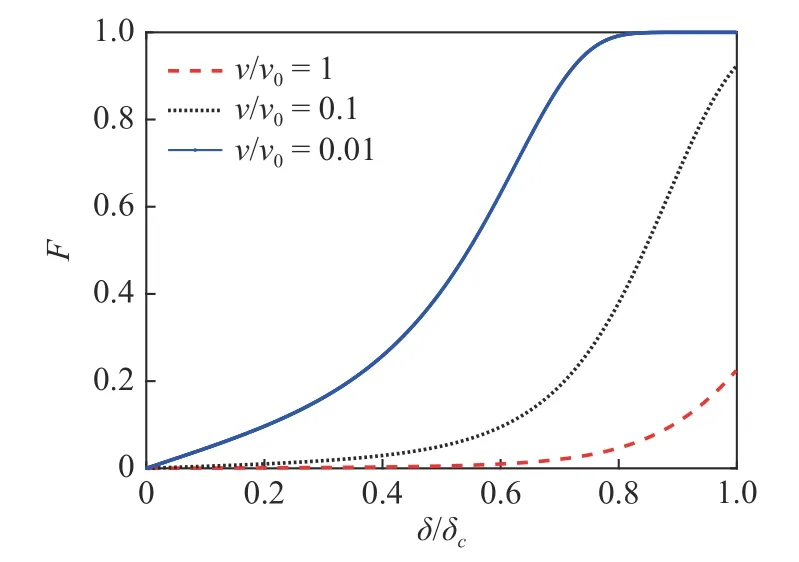
图6 不同加载速率下F 随 δ/δc的变化曲线Fig.6 Evolution of F with δ/δcunder different loading rates

通过引入了应力屏蔽参数 κ 与应变率的相关关系,前述纳-微-细观随机断裂模型扩展到可以适用于不同应变率条件下的分析.

值得指出,上述分析的基础,是将式(40)中概率密度函数关于时间的偏导数取一阶特征值近似.当加载速率较大时,高阶特征值的影响不可忽略[41],所以本文结果仅适用于中、小速率加载情况,不适用于高速率加载情况.

4 本构关系的数值算法

多维弹塑性损伤本构关系的数值计算方法采用Simo等[47]发展的算子分离法,在有限元分析框架中予以实现.这类算法一般分为3 个步骤:弹性预测、塑性修正和损伤修正.算法的基本任务是已知上一时刻tn的基本状态变量的条件下,给定应变增量Δε,求解tn+1时刻的基本状态变量σn+1,

4.1 弹性预测

在弹性预测步中,假定没有塑性演化和损伤演化,按弹性计算试算有效应力

利用损伤能释放率的单调递增标量函数g(Y) 表示损伤面,分别建立受拉和受剪损伤发生准则

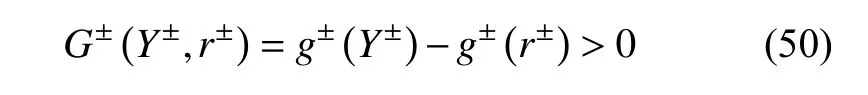
式中,r±决定了当前损伤面大小,表示从0时刻到当前时刻最大损伤能释放率.式(50)表明,只有当损伤能释放率Y±超过历史最大损伤能释放率时,才会导致材料的进一步损伤.

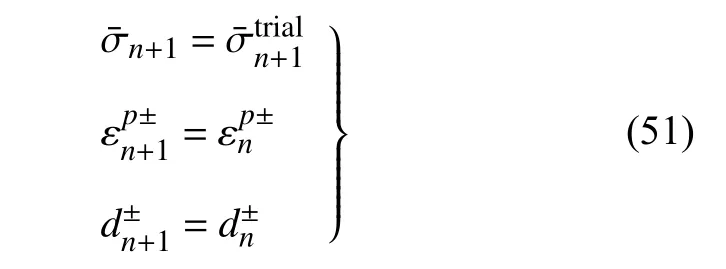
4.2 塑性修正

如果n+1 步的试算损伤能释放率大于历史最大损伤能释放率r±,则进行塑性修正.由于塑性应变和塑性应力间具有等价性,可以通过求解n+1步的塑性应力进行塑性修正,塑性应力定义为

n+1步的有效应力为

将式(55)代入式(54),可解得

由于当前步塑性应力的求解需要当前步的塑性因子,故式(56)为隐式方程,需迭代求解.考虑在每个时间增量步上损伤变量变化很小,可采用前进欧拉算法减少计算量.基于此,塑性应力求解可以表达为

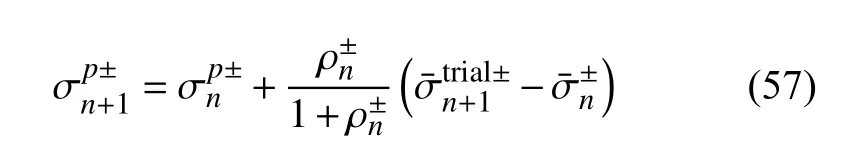
4.3 损伤修正

事实上,在[tn,tn+1] 时间段内Ef的计算中损伤变量和损伤能释放率都是时变的,本质属于隐式方程,可以用Newton-Raphson 方法进行求解.但由于时间增量很小,损伤变量在这一时间增量的变化很小,故可以采用前一步的损伤变量代入.即分析中仅考虑损伤能释放率的时变性.由于这一处理具有显式表达,不需要进行迭代计算,具有明显的算法优势.

5 模型验证

5.1 单轴受拉

取混凝土代表性体积单元进行单轴受拉数值模拟.实验数据取自文献[48].混凝土强度为C50,弹性模量E0=3.5×104N/mm2,试验中加载应变率分别为=1×10-5s-1,=1×10-4s-1和=0.01 s-1.微-细观随机断裂应变随机场分布参数取值来自文献[32],具体为λ+=4.869 6,ζ+=0.582 8,ω+=62.本文模型参数取值为=1×103,=15,=1,p+=18,ξ+=0.3,np+=3.分析中,采用概率空间剖分方法选取100个样本,数值模拟结果与试验数据对比见图7.图例中 m odel-mean和m odel-std 分别表示模型计算应力-应变曲线的均值和标准差.exp-mean和e xp-std 分别是试验数据的均值和标准差.

图7 不同应变率下单轴受拉应力应变曲线均值和标准差对比Fig.7 Comparison of mean and standard deviation of uniaxial tension stress-strain curves under different strain rates

在不同应变率条件下一个典型微弹簧单元载加载过程中的耗能与应变的关系曲线如图8 所示.可见随应变率的增加,微弹簧单元耗能速率降低,从而使得微弹簧断裂发生滞后,导致材料强度提高.

图8 不同应变率下一典型样本Ef随应变的演化Fig.8 Evolution of Efwith strain of a tipical sample under different loading rates

为验证数值算法,选取加载速率为 1×10-5s-1的一个RVE 样本进行了隐式和显式两种数值格式求解结果的对比(图9).可见两种解法给出的结果基本一致,说明显式求解可以兼顾计算精度和求解效率.

图9 隐式求解与显式求解对比Fig.9 Comparison between implicit solution and explicit solution

5.2 单轴受压

对单轴受压代表性体积单元进行与上述类似的数值模拟.试验数据取自文献[32].混凝土强度为C50,弹性模量E0=3.5×104N/mm2,试验中加载应变率分别为=1×10-5s-1,=1×10-4s-1和=3.5×10-2s-1.文献[32] 识别的C50微-细观随机断裂模型单轴受压参数为λ-=7.566 8,ζ-=0.254 6,ω-=84.本文模型参数取值微:=1×10-29,=11,α0-=1,p-=26,ξ-=0.3,np-=2.分析中,采用概率空间剖分方法选取100个样本.数值分析计算的统计特征与试验数据对比见图10,可见理论结果与试验数据符合良好.

图10 不同应变率下单轴受压应力应变曲线均值和标准差对比Fig.10 Comparison of mean and standard deviation of uniaxial compression stress-strain curves under different strain rates

上述分析表明:本文建议模型可以良好地反映混凝土受力力学特征地非线性、随机性与应变率效应.

5.3 动力强度提高因子

为了明确模型的适用范围,针对单轴受拉和单轴受压计算了动力强度提高因子DIF 并与试验数据点进行对比.DIF 定义为动力强度与静力强度的比值,图11 中试验数据点分别取自文献[49]和文献[50],计算中拟静力强度取为 1×10-5s-1.从图11 可以看出,模型不仅能反映强度随应变率增大而提高的趋势,而且计算的均值加减两倍标准差范围能覆盖大部分的离散数据点.从DIF 的对结果来看,模型的适用应变率范围大致在 1×10-7～10s-1,足以覆盖地震中经常出现的应变率范围.

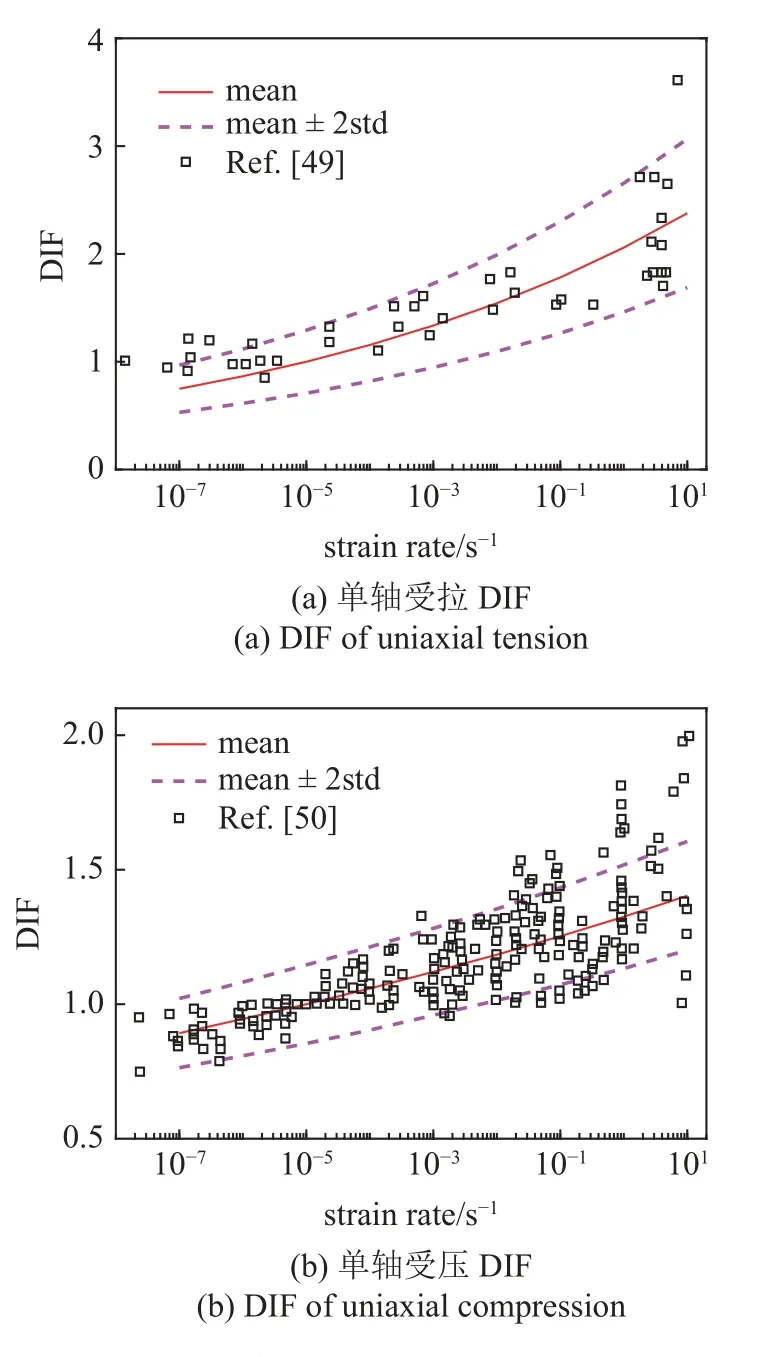
图11 DIF 对比Fig.11 Comparison of the DIF

6 结论

基于速率过程理论分析混凝土材料纳-微观裂纹扩展中的能量耗散过程,经由层级模型与微-细观随机断裂模型相衔接,并引入应变加载速率对裂纹扩展速度的影响,建立了能同时反映混凝土非线性、随机性和率敏感性的混凝土随机损伤本构关系.通过数值模拟与实验结果的对比分析,验证了本文模型的有效性.本文提出模型的适用应变率范围约为 1×10-7～10s-1,可为混凝土结构动力非线性分析、尤其是在地震作用下的分析提供基础.

应当指出:当加载的时间尺度与热激活的时间尺度相当的时候,速率过程理论所计算的逃逸速率不再准确.因此,速率过程理论在高应变速率条件下不再适用.在高应变速率条件下的混凝土动力本构关系,尚需进一步研究.