基于非线性分析的加肋板肋条位置无网格优化1)

彭林欣 李知闲 项嘉诚 覃霞

*(广西大学土木建筑工程学院,南宁 530004)

†(广西大学广西防灾减灾与工程安全重点实验室,工程防灾与结构安全教育部重点实验室,南宁 530004)

引言

建筑物筏形基础、混凝土刚性路面板、机场跑道、钢箱梁等板壳结构在不均匀载荷的长期影响下,结构易发生倾斜、变形、开裂等问题.筏形基础等结构本质上就是加肋板,如果在设计阶段通过优化肋条布置来调整结构的局部刚度,有针对性地适应载荷的局部不均匀性,可达到控制结构不均匀变形、改善结构力学性能等目的.

近年来各种优化理论已被普遍应用到结构工程中[1-14],如Yi等[1]基于有限变形弹塑性壳体结构,对球面曲壳进行了无网格法结构优化设计;彭细荣等[2]考虑了连续体在破损-安全下的结构拓扑优化问题,避免结构过于高效而缺少适当的冗余结构,因此对局部破坏过于敏感;陈炉云等[3]采用遗传算法对对称型复合材料板结构进行了结构-声辐射铺层的几何优化分析;李林远等[4]对矩形加肋板的肋条布置进行了无网格法优化,结合混合遗传算法,使横向载荷的作用下的加肋板中心点挠度最小;王选等[7]针对体积和应力约束下的最小柔顺性问题提出了一种改进的双向渐进结构优化方法.

基于单元的优化分析方法在每一次肋条位置改变时都需要重新划分单元,从而增加了优化的计算量.而无网格法[15]不需要划分单元,而是在一系列离散点上进行计算,是基于点的近似,摆脱了单元的限制.近年来无网格法在国内外学者的研究探索下得到进一步发展[15-29].彭林欣[21]提出一种求解矩形加肋板线性弯曲问题的移动最小二乘无网格法;杨柳和彭建设[24]采用常微分方程解法分析了平行四边形板的弯曲问题;方电新等[26]根据变分原理,采用罚函数法满足本征边界条件,得到平板弯曲计算的无网格法控制方程,分析求解了平板的弯曲问题;曾军才等[27]应用改进傅里叶级数方法,建立了正交各向异性矩形薄板的弯曲振动模型,并求出控制方程在各种边界条件下的解析解;Zhou等[28]使用移动最小二乘法研究分析菱形板的自由振动,解决了菱形板钝角处的应力奇异性导致收敛速度慢的问题.

由以上分析可知,目前多数无网格方法研究都集中在平板的拓扑优化分析,而基于几何非线性的加肋非矩形板肋条位置优化问题鲜见相关文献.为此,本文基于一阶剪切变形理论[29]和移动最小二乘法[15],提出加肋非矩形板无网格模型,并结合遗传算法根据实际需要优化加肋非矩形板的肋条位置,调整加肋板的局部刚度,以减小不均匀变形并增加其自振频率.以肋条在非矩形板上的位置为设计变量,依次以加肋非矩形板的最大频率、控制点的最小挠度为目标函数,对肋条的布置进行优化.文末以不同参数、载荷布置形式的加肋圆板和加肋平行四边形板的肋条最佳布置位置进行分析求解,研究结果表明,该方法能有效地分析考虑了几何非线性影响的非矩形加肋板优化问题,且在肋条位置改变时,不需要重新划分网格,极大地降低了计算量,具有一定的工程实用价值.

1 加肋非矩形板的无网格模型

1.1 近似场函数

本文将加肋非矩形板视为非矩形平板与肋条的组合结构,并用梁模型来模拟肋条.分别采用一系列的点来离散非矩形平板和肋条(记平板的离散节点数为np,肋条的离散节点数为ns),同时采用不同的坐标系分别建立圆形平板(x,y,z)和梁的无网格模型,如图1 所示.本文忽略肋条的扭转刚度和平面外刚度,并且假定肋条与平板的材料属性相同,其中R,hp,hs和ts分别为圆板平板半径、板厚、肋条高和肋条宽,如图2 所示.圆形平板和肋条为均质材料,弹性模量和泊松比分别记为E和μ.

图1 加肋圆板的无网格模型Fig.1 The meshless model of the circular stiffened plate

图2 加肋圆板Fig.2 The circular stiffened plate

为方便后续推导,假设平板上每个节点的自由度(DOF)为(up,vp,wp,φpx,φpy),up,vp和wp分别是沿x,y和z方向的平动位移.φpx和φpy分别是绕y和x轴的旋转角度.基于一阶剪切变形理论(FSDT),φpx,φpy与wp相互独立.另外,[u0pI,v0pI,wpI,φpxI,φpyI]T=ΔpI为平板离散节点I参数,u0pI,v0pI和wpI分别为离散节点I在中面上沿x,y和z方向的平动位移.

对于肋条,假设其DOF为(us,ws,φs),us和ws分别为沿着和的平动位移,φs为绕旋转的角度,并且与ws独立.另外,[u0sI,wsI,φsI]T=ΔsI肋条离散节点I的参数.u0sI为肋条离散节点I在中面上沿的平动位移.

根据一阶剪切变形理论[29]和移动最小二乘法[15],可以得到非矩形平板的位移场为

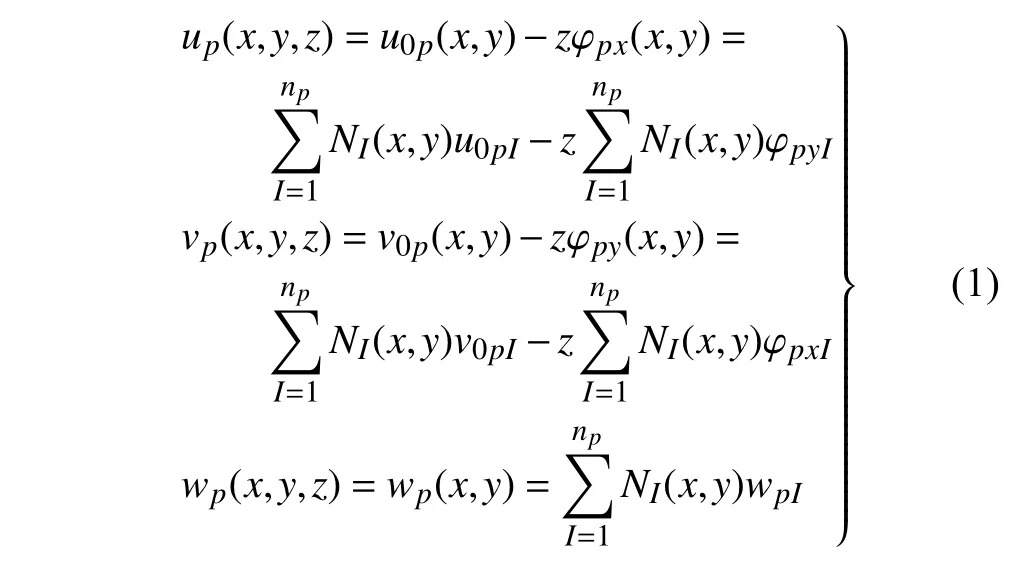
将式(1)写成矩阵形式,有

肋条的位移场为

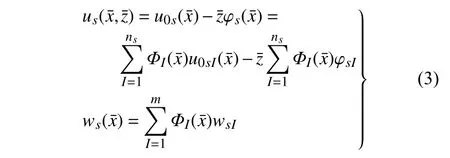
将式(3)写成矩阵形式,有

式中,scale为影响域系数;cI为影响域基数,取节点xI与距其最近节点的间距.

菱形板相对于圆板存在边界处的角度变换问题,使用变支撑半径的动态影响域能够更好对边界进行处理,因此本文针对加肋菱形板所出现的应力集中现象,选择变支撑半径的动态影响域,而对于加肋圆板,则采用等支撑半径的静态影响域.

由于式(1)和式(3)中的形函数不满足克罗内克条件,各节点未知量是节点参数而非节点真实位移,所以板与肋条的位移协调不能像有限元那样通过节点未知量直接施加,而需另寻途径.本文通过肋条和平板上两点连线和接触面的交点建立肋条节点和平板节点的位移协调条件,从而将肋条和平板的刚度矩阵进行叠加.如图4 所示,肋条上任一点S,必定在平板上存在对应点P(P点不一定是平板上的离散节点),使得P和C两点连线垂直于xy面,C点为P和S两点连线与板面的交点,同心肋条时三点重合.

图4 位移协调示意图Fig.4 Indication of displacement coordination

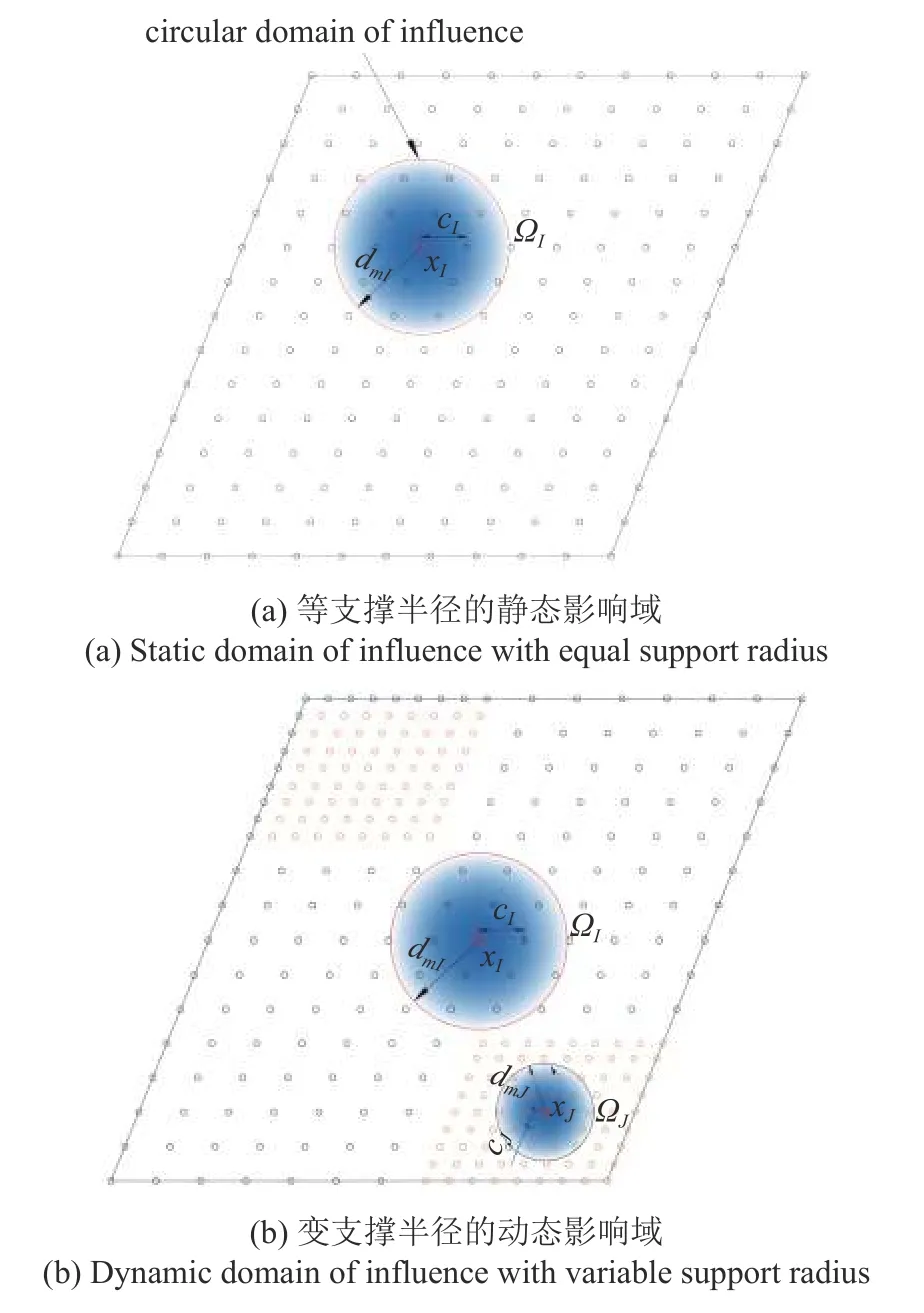
图3 圆形影响域Fig.3 Circular domain of influence

在C点有以下的位移协调关系

对于肋条上的每个离散节点(离散节点数为ns个),都可以在板上找到一个点与之对应.于是,式(7)、式(8)和式(9) 分别有ns个关系,并基于FSDT 有

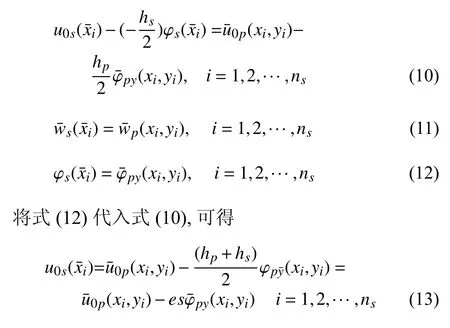
式中,es为肋条与板中心点间的距离,对于同心肋条,es=0.将式(11)、式(12)和式(13)写成矩阵形式,有

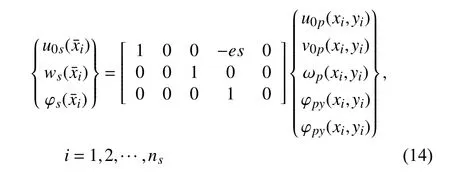
将式(6)代如式(14),有

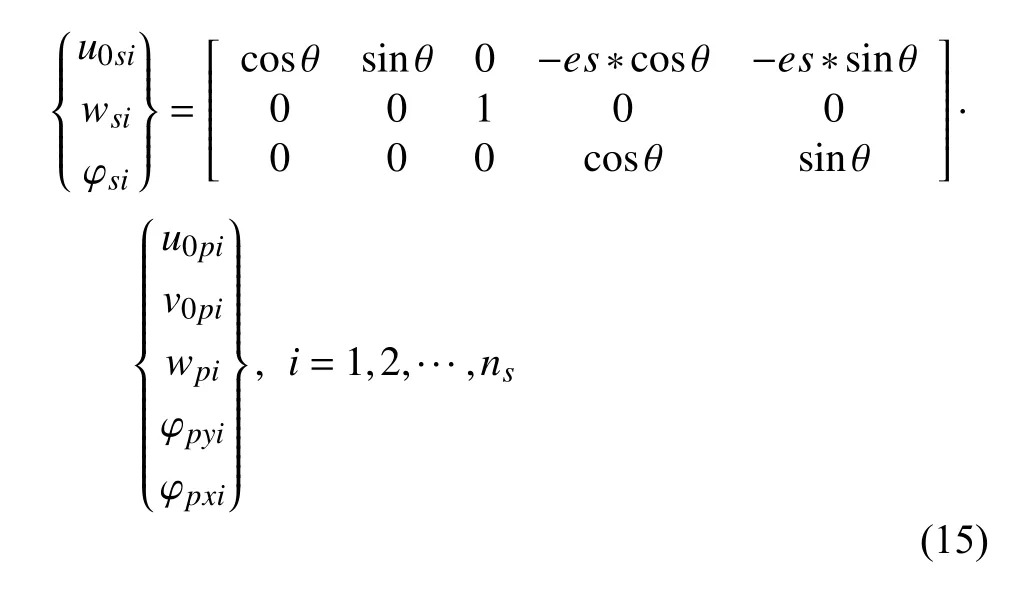
由移动最小二乘法可以知

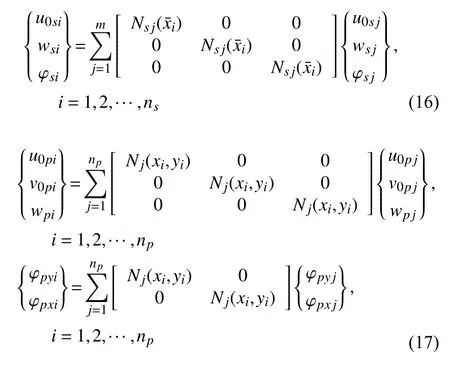
式(17)的np为非矩形平板的离散节点数,将式(16)和式(17)代入式(15),并写成矩阵形式,可以得到

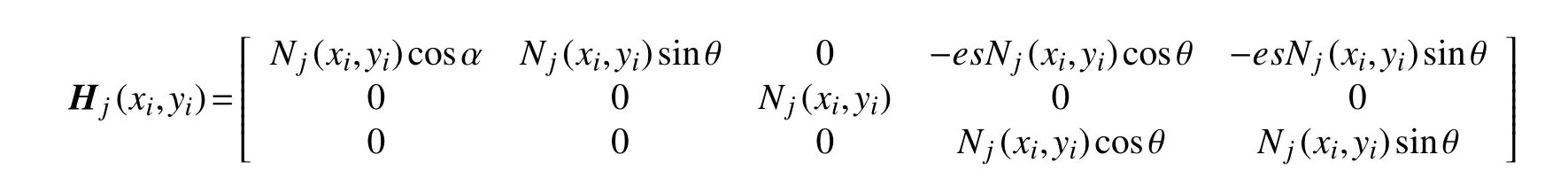
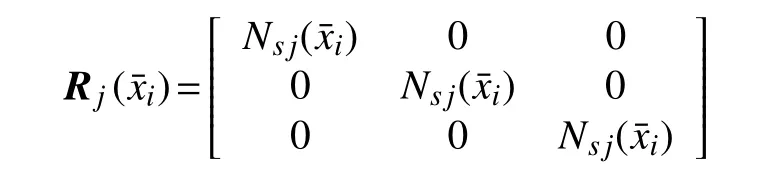
由式(18)可导出

矩阵Tsp即为节点参数转换矩阵,其与Ts及Tp有关.若肋条改变位置时,则肋条节点对应板上的点(xi,yi)发生变化,需要重新计算Nj(xi,yi)及Tp,但在肋条上的点的坐标不会发生变化,所以不需重新计算Rj()及Ts.通过矩阵Tsp可以成功地将肋条添加到平板上,从而得到加肋非矩形板(复合结构)的无网格模型.该无网格模型可以任意改变肋条位置,而不需要重新布置平板的节点,避免网格重构.

1.2 应力集中处的处理

如5 所示,在钝角处(变形及应力梯度太大)作扇形或规则网格形加密布置离散节点,以保证计算精度.带有加密区的非矩形板,其离散节点的影响域采用动态影响域,而所有肋条均采用静态影响域,以获得更精确的计算结果.对于动态影响域,本文通过固定影响域内离散节点数的方法确定其支撑半径.后续算例中,以控制影响域内离散节点数为20个为准.

图5 离散节点加密Fig.5 The encryption of discrete nodes

2 加肋非矩形板的几何非线性列式

2.1 非矩形板应变和应力

非矩形板的位移场如式(1),根据冯·卡门大挠度理论,可以得到非矩形板的应变如下

2.2 肋条的应变和应力

肋条的位移场如式(3),根据冯·卡门大挠度理论,可以得到肋条的应变

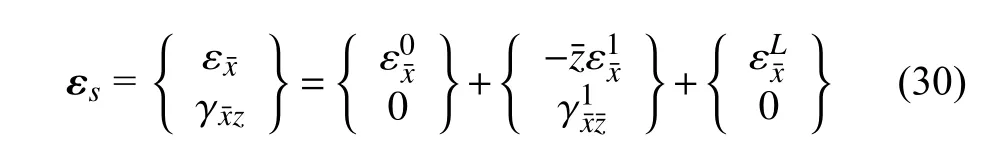
为方便说明,将式(30)写成

2.3 非线性问题的平衡微分方程

根据以上推导的非矩形板和肋条的应力、应变,以及外力的虚功,可以导出非线性问题的平衡微分方程

式中,F为载荷向量(例如,当加肋圆板受面外均布力q(x,y)和集中力P的作用时,见图6.如下

图6 受面外均布力和集中力P 作用的加肋圆板Fig.6 A circular stiffened plate subject to an out-plane force and concentrated force P

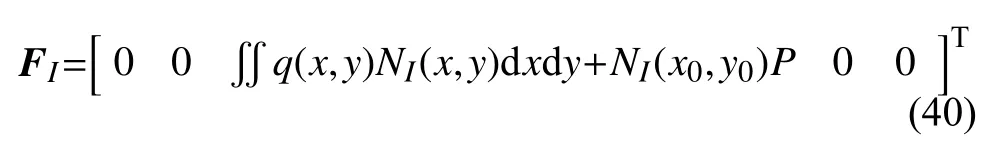
将式(19)、式(27)和式(36)一同代入式(39),可以得到

将式(19)、式(28)、式(29)、式(37)和式(38)代入式(43),可以得到

Ss=Asσ,As为肋条横截面面积.

从式(42)可以得到

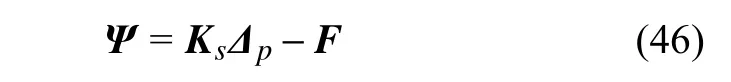
本文采用Newton-Raphson 方法[33]来求解非线性方程.

3 加肋非矩形板的自由振动列式

3.1 平板动能

基于一阶剪切变形理论[29]及移动最小二乘法[15],非矩形板以时间、空间为变量的位移场为式

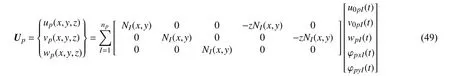
则其速度Vp为位移Up对时间t求导,即

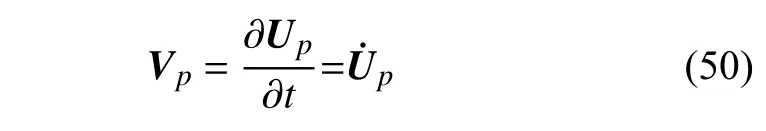
将式(49)代入式(50),可以得到

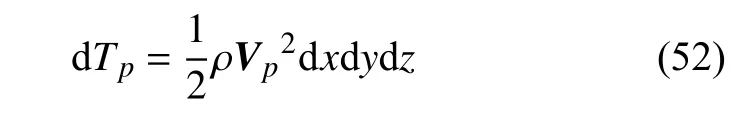
在整个非矩形板内进行积分,可以得到整块平板的动能为

将式(51)代入式(53),得平板的动能为

3.2 肋条动能

肋条以时间、空间为变量的位移场为式

则其速度Vs为位移Us对时间t求导,即

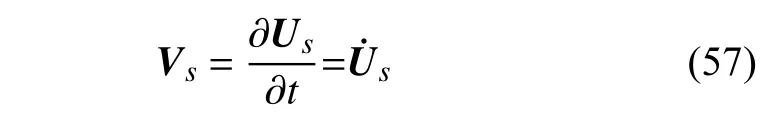
将式(56)代入式(57),可以得到

在整个肋条内进行积分,可以得到整个肋条的动能为

将式(59)代入式(60),得肋条的动能为

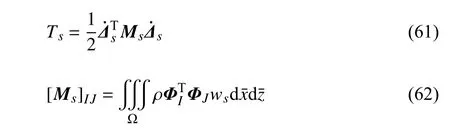
当非矩形板上有多个肋条时,可以按照类似的方法肋条的动能依次叠加到平板上.若是肋条的几何尺寸及材料没有改变,只是摆放位置不同,不需重复计算每根肋条的弹性刚度矩阵,只需计算Tp矩阵.

3.3 自由振动控制方程

结合文献[34],可以得到加肋板的应变势能为

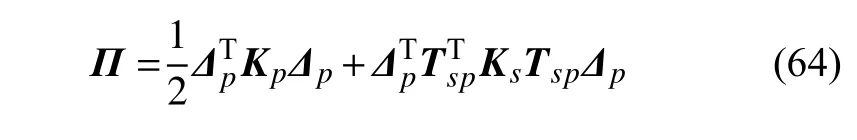
将式(54)和式(63)进行叠加,可以得到整个加肋板的动能

由Hamilton 原理,可以得到加肋非矩形板的自由振动问题的控制方程

通过完全转换法处理本质边界条件,可以得到以真实节点位移为未知量的加肋板自由振动控制方程

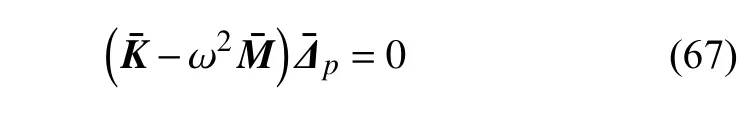
代入边界条件求解方程,可以得到结构的自振频率

4 算例分析

以菱形及加肋圆板(单肋条板及垂直双肋条板)为例,先通过受均布载荷作用的单肋条菱形板的肋条位置优化分析验证本文算法的准确性,再采用遗传算法[35]优化局部载荷作用下单肋、双肋菱形及圆形板的肋条位置,控制板中点挠度最小和最大化加肋板的自振频率.

在遗传算法优化中,本文使用rand 函数在非矩形板上随机生成肋条的20个初始位置,采用轮盘赌选择法,单点交叉算子(交叉概率Pc=0.5),基本位变异方式(变异概率Pm=0.1),并利用连续几代的个体适应度的平均值(或方差)作为终止准则,反复迭代计算找出最优解.

4.1 加肋菱形板控制点最小挠度肋条位置优化

4.1.1 本文优化方法的有效性分析

一四边铰支的加肋菱形板(图7),E=68 GPa,μ=0.27,hs=0.08 m,hp,ts均为0.01 m,l1=l2=1.5 m.加肋菱形板受均布载荷作用q=50kN/m²,显然在该载荷作用下使板中点挠度最小的肋条最优位置为x=0.75 m.现采用本文所述的方法进行10次优化分析:种群数选为20(编号为1 至20),遗传终止迭代的次数定为30,无网格方案为n=10.10次优化分析结果见表1,相应的波动曲线如图8 所示.

图8 均布荷载作用下本文解与理论解的对比Fig.8 Comparison of the presented solution and the theoretical solution

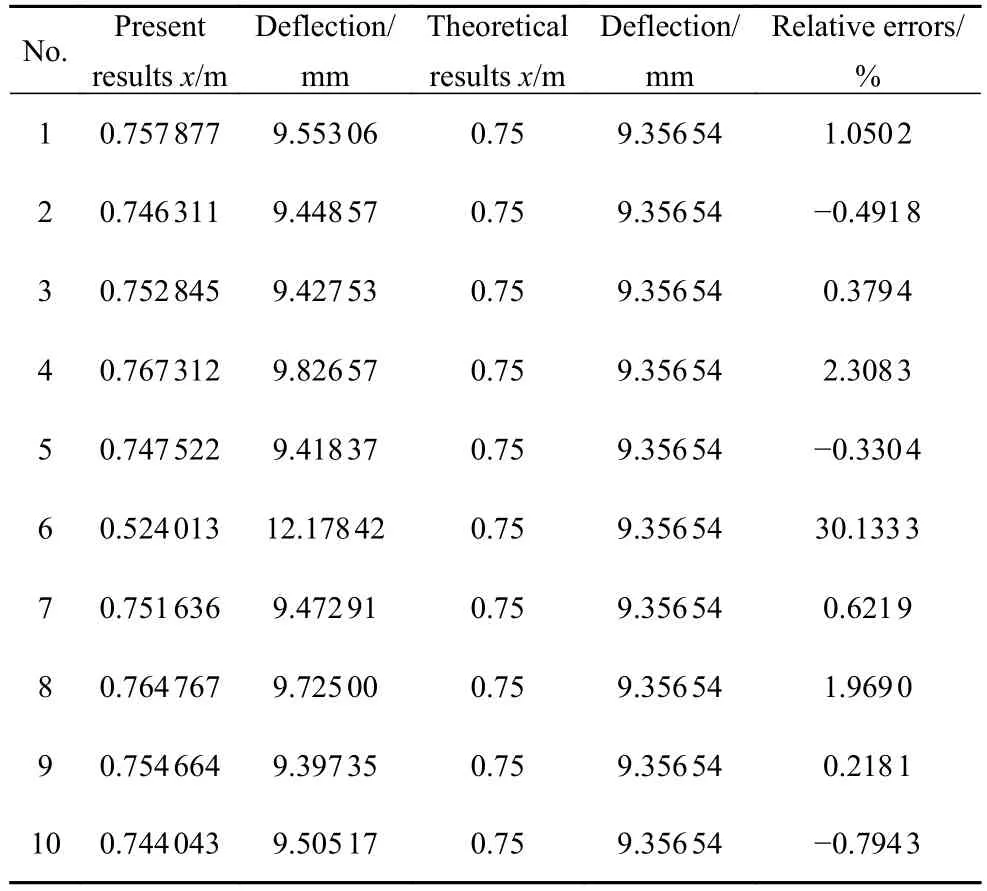
表1 均布荷载下加肋菱形板肋条位置10次优化结果Table 1 Results of rib position optimization of the skew stiffened plate under uniformly distributed load

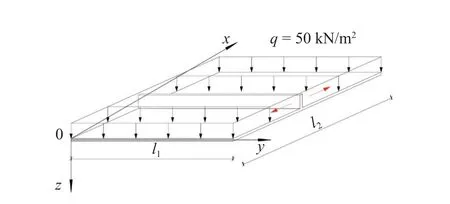
图7 受均布荷载作用的单肋菱形板Fig.7 Single stiffener stiffened plate subjected to uniformly distributed load

结果表明:在十次优化结果中,除第6 次优化结果误差相对较大(30.133 3%),其余的相对误差均在3%以内,其中第9 的优化结果最佳.第6 次计算结果误差相对较大的主要原因是:遗传算法在迭代过程中会出现陷入局部最优解的情况.以下分别就第9 次和第6 次的结果作详细分析:

(1) 第9 次计算结果分析:第9 组数据迭代1 次、10次、20次及30次的种群分布情况如图9所示(虚线位置x=0.75 m为本算例最优解),并以样本方差式描述肋条的位置与最优解之间的偏离程度.

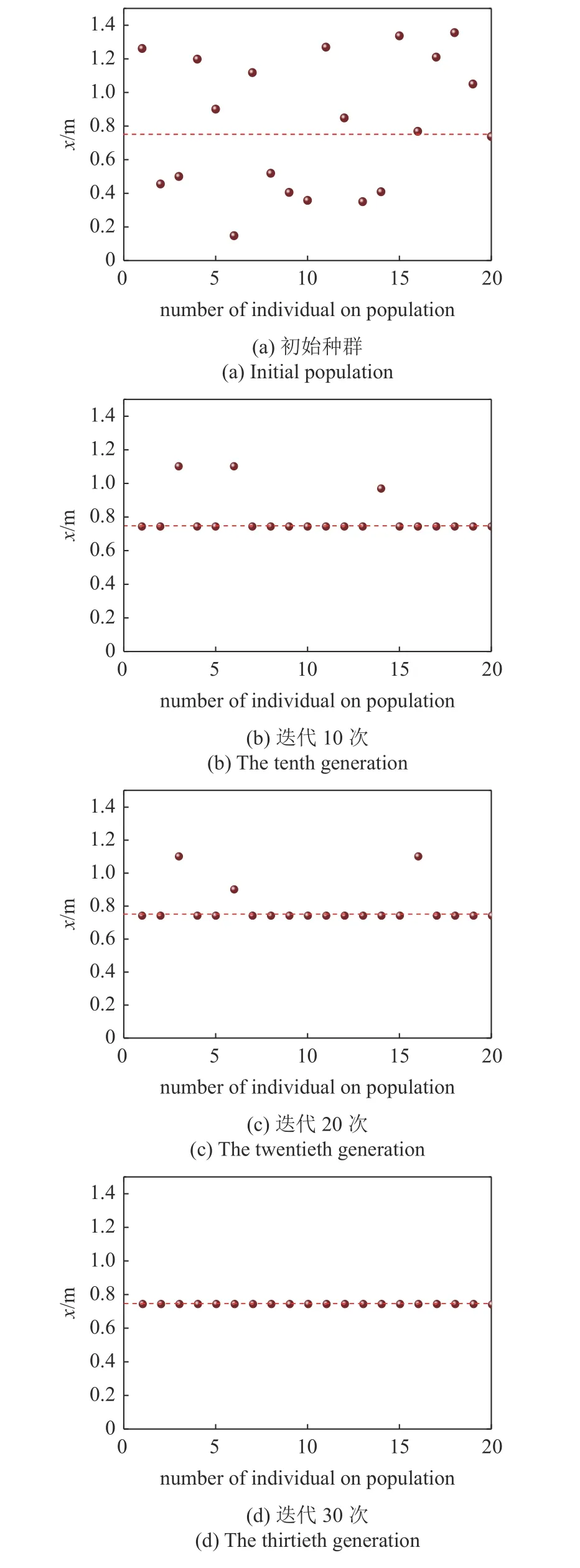
图9 均布荷载作用下单肋条优化迭代过程的种群分布(第9 次计算结果)Fig.9 Population distribution of single rib optimization iterative process under uniform load(the 9th result)

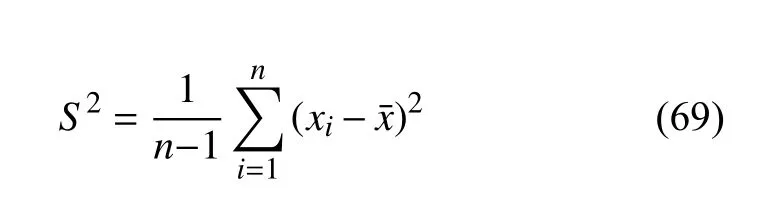
式中,n为样本容量,即种群个体的数目,取值为20,随机变量xi为肋条的位置,为最优解,本算例中=0.75 m,初始种群、迭代10次、20次及30次的方差分别为0.159 3,0.015 5,0.014 2,0.0018.

由图9 可知随着迭代次数的增加,种群中的优势个体逐渐增多,个体逐步向最优解靠近,当迭代次数达到一定值时结果收敛,证明了遗传算法的有效性.由第10代和第20代种群的分布发现,在同一代种群中(或者不同代种群之间)有些个体是相同的,这是由于在遗传算法的迭代中大概率是种群里适应度高的个体参与到下一步运算,从而引起部分个体重复出现.每一代的最优解逐渐向全局最优解(x=0.75 m)靠近,第10代的种群中已出现17 个相同且优质个体,直至第30代,种群中所有个体均相同且优质,即结果收敛于最优解.此外,由初始种群的分布图可知个体在0～ 1.5 m 范围内随机且分散分布,说明了遗传算法在优化过程中搜索的随机性和全局寻优性能.

(2) 第6 次计算结果分析:第6 组数据迭代一次、10次、20次及30次的种群分布情况如图10所示,方差计算结果分别为0.189,0.049,0.061,0.052.结果表明:随着迭代次数的增加,群体的总体分布趋势亦是逐渐向最优解靠近,但最终收敛于一个局部最优解(在最优解附近),且在进化过程中出现了优势个体丢失的情况,例如第一代出现了个体最优点x=0.762 m,却在第10代丢失.这主要是由于传统的遗传体制和根据适应度进行比例选择的保留策略,会让适应度值大的优势个体在下一代进化选择中得到相对较多的取样,而某些适应性较差的劣势个体则被过早丢弃,随着迭代代数的递增,产生了局部最优解.

图10 均布荷载作用下单肋条优化迭代过程的种群分布(第6 次计算结果)Fig.10 Population distribution of single rib optimization iterative process under uniform load(the 6th result)

以上研究表明:本文方法可以找出肋条的最佳位置,在特定载荷和边界的情况下使得加肋圆板的中点挠度最小.另外在寻优过程中可能出现收敛于局部最优解的现象,需要通过多次计算,对比所得结果找出最优解以保证准确性.

4.1.2 局部载荷作用的单肋条位置优化

在4.1.1 节算例的基础上将均布载荷改成局部载荷,载荷大小改为100kN/m²,其余参数不变,如图11 所示.进行十次优化计算,结果见表2,表明第10次计算结果最优,控制点(板中点) 的位移最小(5.057 41 mm),故选x=0.662 906 m为最优解.第10组初始种群、迭代10次、20次以及30次的种群分布情况图12(虚线位置x=0.662 906 m),其样本方差分别为0.057,0.036,0.022,0.014.结果表明:随着迭代次数的递增种群逐渐向最优点靠近,最终可求出在相应载荷作用下加肋菱形板使控制点挠度最小的肋条最佳摆放位置.

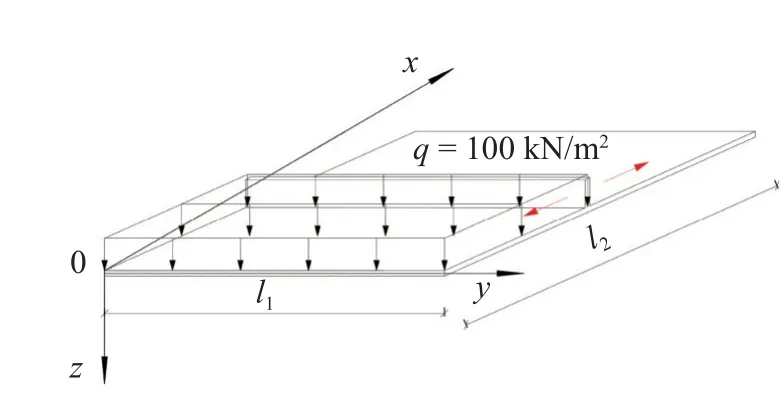
图11 局部荷载下单肋条菱形板Fig.11 Single-stiffened skew plate under local load

表2 局部布荷载下双肋条位置优化结果Table 2 Results of rib position optimization under local load

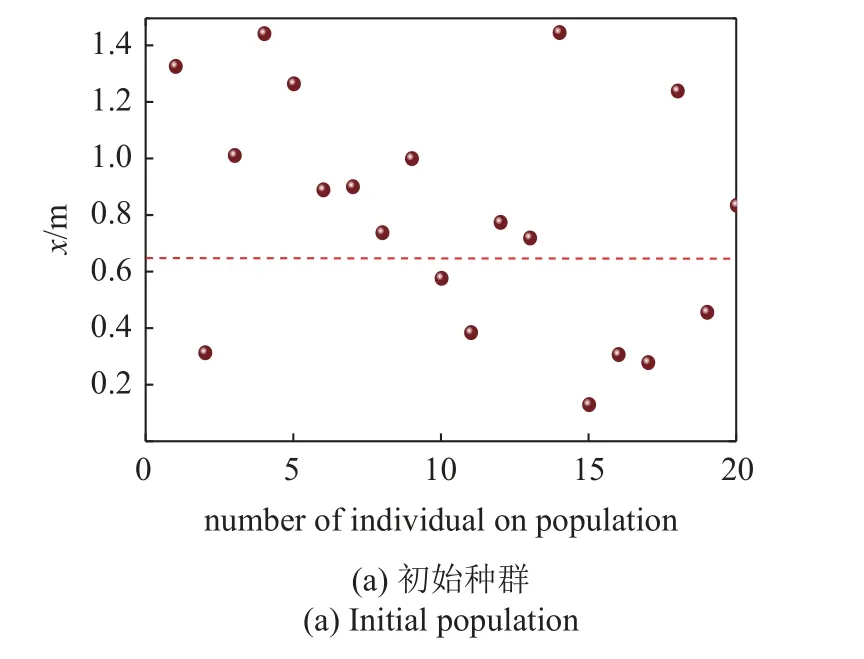
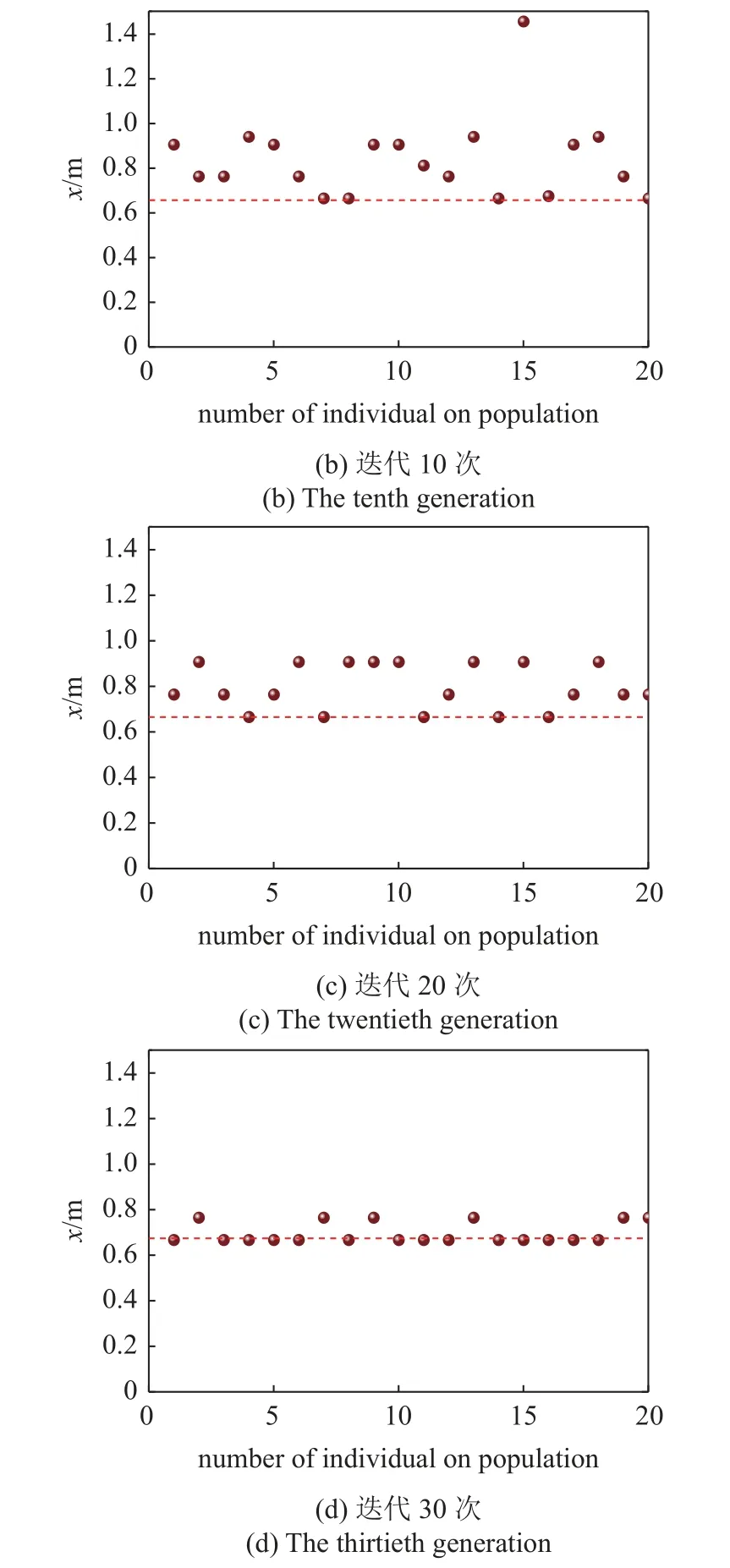
图12 局部荷载作用下单肋条优化迭代过程的种群分布Fig.12 Population distribution of single rib optimization iterative process under local load

4.1.3 局部载荷作用的双肋条位置优化

在4.1.2 节算例的基础上增加肋条(记为肋条Ⅰ和肋条Ⅱ),载荷变为180kN/m²,如图13 所示.考虑局部载荷作用对肋条Ⅰ(平行于底边)和肋条Ⅱ(平行于斜边)的位置进行优化(仅考虑平移).此时优化计算包含两个设计变量,即肋条Ⅰ的x1和肋条Ⅱ的x2,种群个数取为30个,十次优化计算结果见表3,表明第6 次计算结果最优,菱形板的控制点挠度位移最小(5.979 mm),故选肋条Ⅰx1=0.65012 m、肋条Ⅱx2=0.621 33 m为最优解.初始种群、迭代10次、20次及30次的种群分布如图14 所示(虚线位置x1=0.65012 m,x2=0.621 33 m),样本方差见分别为0.502,0.261,0.115,0.085.

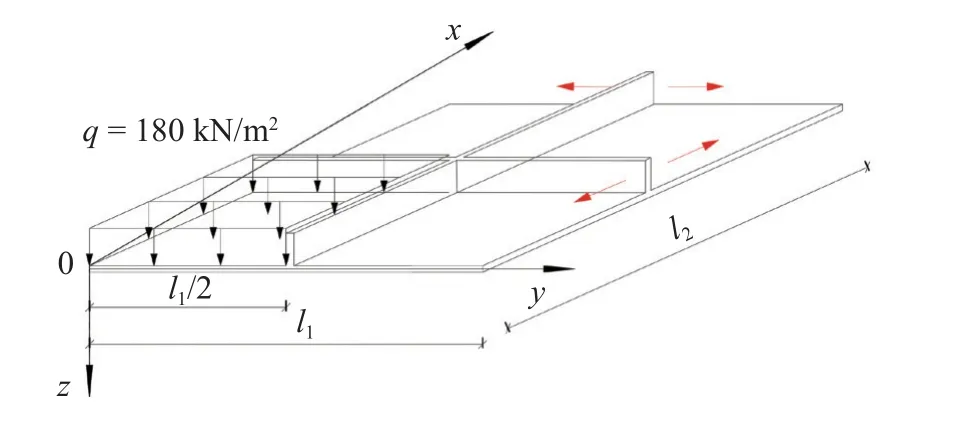
图13 局部荷载下双肋条菱形板Fig.13 Double-stiffened skew plate under local load

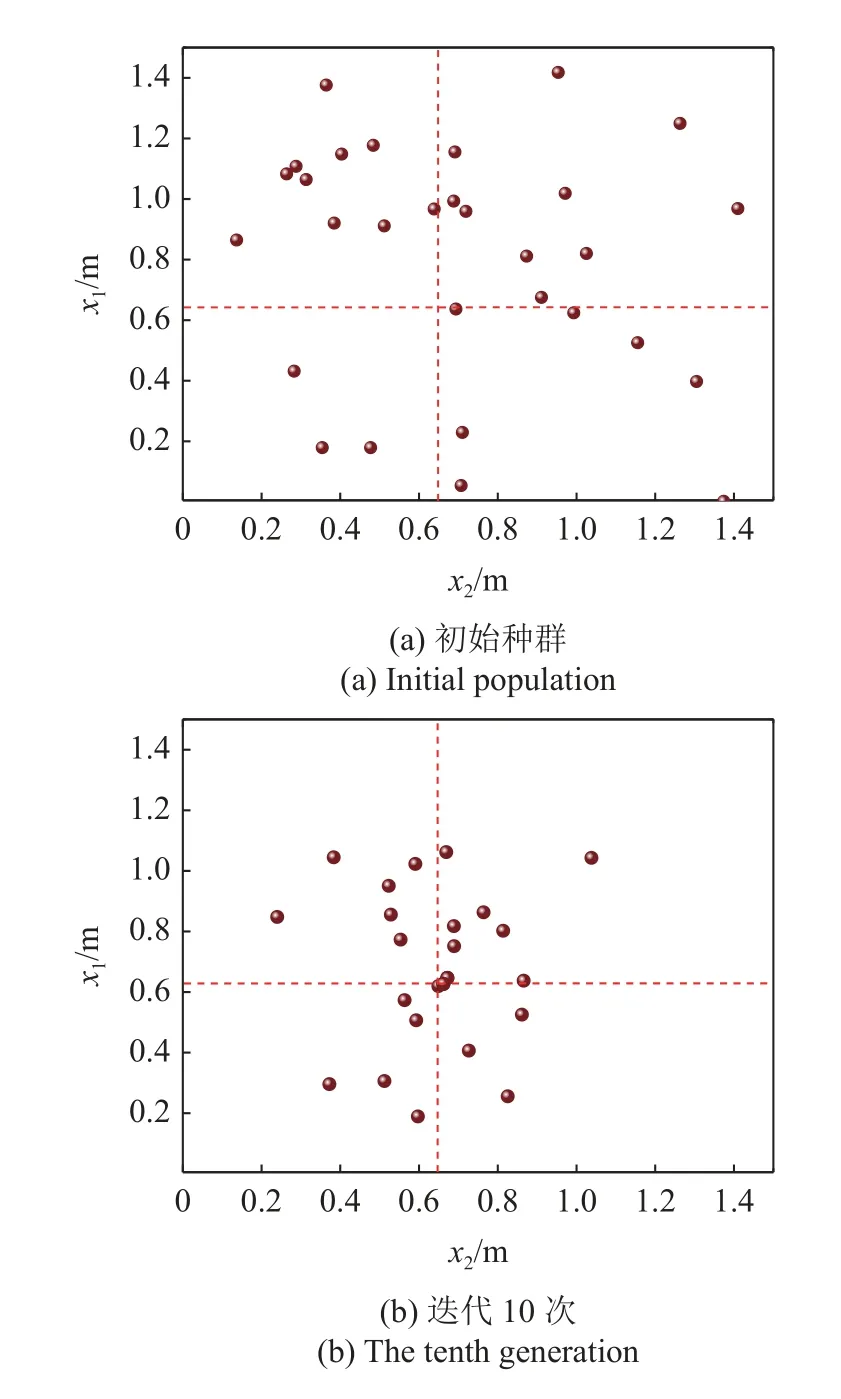
图14 局部荷载作用下双肋条优化迭代过程的种群分布Fig.14 Population distribution of double-rib optimization iterative process under local load

表3 局部布荷载下双肋条位置优化结果Table 3 Results of double ribs position optimization under local load

由种群分布图及方差结果可看出:随着迭代次数的递增种群逐渐向最优解靠近,最终求出局部载荷作用下肋条的最佳摆放位置,说明本文方法在包含多个变量的双肋条板优化方面亦是有效的.对比4.1.1和4.1.2 节算例的单肋优化结果及4.1.3 节的双肋优化结果,可以发现,对单肋的位置进行优化时,随着迭代次数的增加,种群的个体收敛更快,且最后收敛于同一位置的概率更大,对双肋的位置进行优化时,即使迭代到30代,种群个体中仍存在一些较差的个体,且收敛于同一位置的概率相对较小.主要是由于双肋的位置优化增加了设计变量,个体变异的随机性更大,且优化问题相对复杂.

4.2 加肋圆板最大频率肋条位置优化

4.2.1 单肋条位置优化

一周边铰支的加肋圆板如图15 所示(圆板中有一固定肋条Ⅰ),R=0.8 m,hs=0.08 m,hp和ts均为0.01 m,E=210GPa,μ=0.3,ρ=7800kg/m³.现优化肋条Ⅱ的(旋转)位置,使加肋圆板的一阶自振频率最大化.设计变量为肋条Ⅱ与x轴的夹角θ,约束条件为θ∈[0,π/2].采用本文所述的方法进行10次优化分析:种群数选为20(编号为1～ 20),遗传终止迭代的次数定为30,无网格方案为n=10,10次优化分析结果见表4.

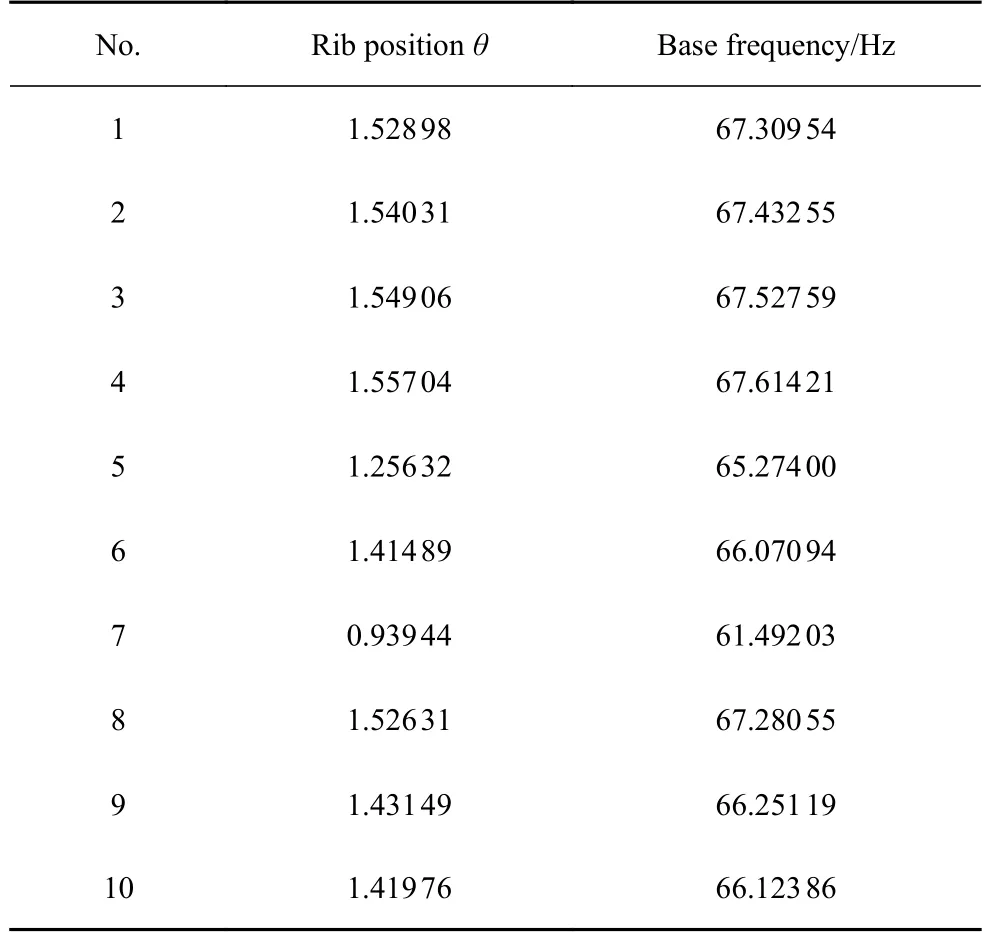
表4 加肋圆板单肋条位置优化结果Table 4 Results of rib position optimization of circular stiffened plate

图15 双肋条加肋圆板Fig.15 Circular stiffened plate with two stiffeners

表明第3 次计算结果最优,加肋圆板频率最大(67.527 59),故选肋条Ⅱθ=1.54906 rad为最优解.第3 次计算的初始种群、迭代10次、20次及30次的种群分布如图16 所示(虚线位置θ1=1.54906

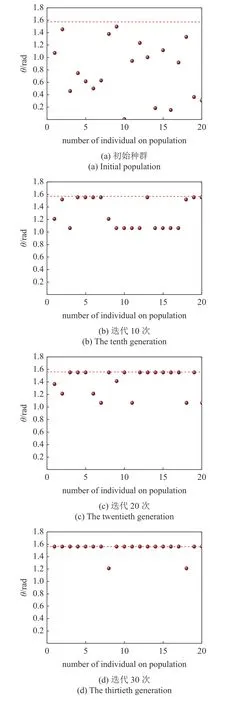
图16 加肋圆板单肋条优化迭代过程的种群分布Fig.16 Population distribution of single rib optimization iterative process of circular stiffened plate

rad),样本方差分别为0.813,0.123,0.064,0.012.由种群分布图及方差结果可看出:随着迭代次数的递增种群逐渐向最优解靠近,最终求出使加肋板的基频最大化的肋条最佳摆放位置.

4.2.2 双肋条位置优化

一直边固定的加肋半圆板如图17 所示,R=0.8 m,hs=0.06 m,hp,ts均为0.01 m,E=210GPa,μ=0.3.半圆形板上有肋条Ⅰ和肋条Ⅱ,现优化肋条Ⅰ和肋条Ⅱ的(旋转)位置,使加肋半圆板的一阶自振频率最大化.肋条Ⅰ和肋条Ⅱ的设计变量分别为θ1(肋条Ⅰ与x的夹角)和θ2(肋条Ⅱ与y的夹角),约束条件为θ1∈[0,π/2],θ2∈[0,π/2].采用本文所述的方法进行10次优化分析:种群数选为20(编号为1 至20),遗传终止迭代的次数定为30,无网格方案为n=10,10次优化分析结果表5.

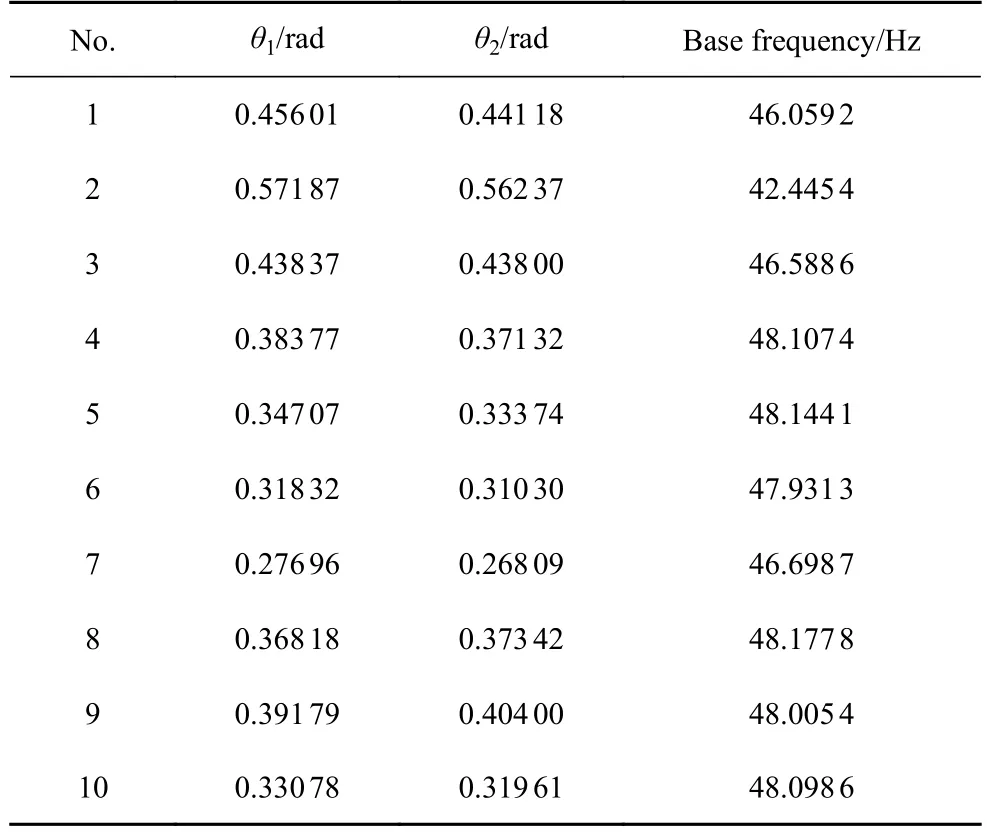
表5 加肋半圆板条位置优化结果Table 5 Results of double ribs position optimization of semicircular stiffened plate

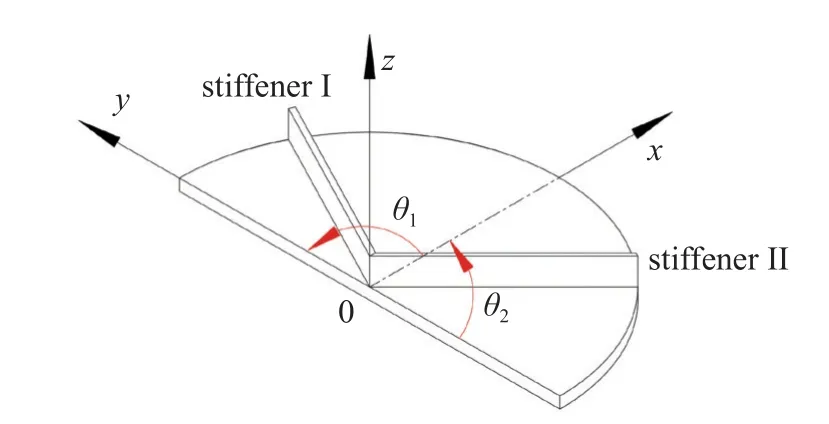
图17 双肋条加肋圆板Fig.17 Circular stiffened plate with two stiffeners

表明第8 次计算结果最优,菱形板的控制点挠度位移最小(48.177 8),故选肋条Ⅰθ1=0.368 18 rad和肋条Ⅱθ2=0.373 42为最优解.第8 次计算的初始种群、迭代10次、20次及30次的种群分布如图18 所示(虚线位置θ1=0.368 18 rad和肋条Ⅱθ2=0.373 42),样本方差分别为0.825,0.291,0.154,0.07.由种群分布图及方差结果可看出:随着迭代次数的递增种群逐渐向最优解靠近,且前10代的种群收敛速度相对较快,最终求出使半圆加肋板的基频最大化的肋条最佳摆放位置.

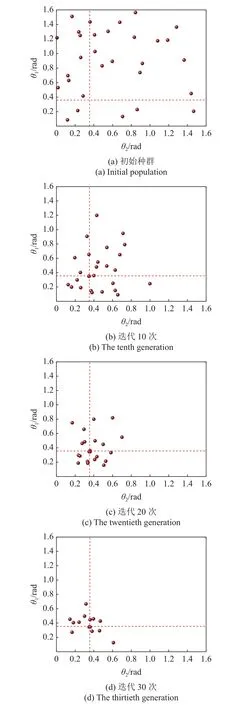
图18 加肋半圆板肋条优化迭代过程的种群分布Fig.18 Population distribution of double-rib optimization iterative process of semicircular stiffened plate

5 结论

本文提出了加肋非矩形板肋条位置优化的无网格分析方法,通过不同的算例分析,得出如下结论:

(1)基于遗传算法所提出的肋条位置无网格优化方法,可有效优化加肋非矩形板的肋条位置,使控制点的挠度最小或自振频率最大:在特定条件下(载荷、边界、加肋板形状),随着优化迭代次数的递增,最终可找出相应条件下肋条的最佳摆放位置.

(2)在优化计算中,遗传算法用来进行样本选择,再通过本文所建立的加肋非矩形板无网格模型进行计算,优化结果可能收敛于局部最优解,因此需要进行多次优化计算,通过对比分析来选出最优解.

(3)本文建立的肋条与非矩形板之间的节点参数转换方程,完全基于离散点得到问题的近似数值解,点与点之间没有单元或其他的直接连接,即使在优化过程中肋条位置不断改变也不会导致平板节点重新分布,因此,可以实现肋条在平板上按任意位置布置,且可在保证计算结果满足所需精度的情况下保持平板的离散方案不变.在每一次优化进程中,仅需要重新计算式(20)的Tp矩阵,在考虑几何非线性影响的前提下,成功省去了繁杂的网格重置工作,极大地减少了计算量,在工程实际上具有一定的优势.