近似不可压软材料动力分析的完全拉格朗日物质点法1)

章子健 刘振海 张洪武 郑勇刚

(大连理工大学工程力学系,工业装备结构分析国家重点实验室,辽宁大连 116024)

引言

软材料广泛存在于自然界和工程中,如水凝胶、形状记忆聚合物等一些非线性弹性体,以及人体或动物的组织和器官等一些生物材料[1].软材料往往具有高弹性、低模量、耐磨性、抗震性等优良特性,并且在经历极大的变形时没有能量耗散[2],因此在生活和工程中得到了广泛的应用.对于这些软材料力学行为的分析主要包括理论[3]、实验[4]和数值模拟[5]3 种,其中数值模拟相较理论方法适用范围更广,并且不受实验环境和设备的制约[6].因此,针对软材料力学行为分析的数值方法在近年来得到持续地发展和广泛地应用.

有限单元法FEM 作为模拟固体力学行为最常用的一种数值方法,被广泛地运用于模拟软材料的各种复杂变形[7-8].由于软材料往往具有不可压或近似不可压特性,因此在处理该类材料时需要对算法进行特殊处理.常见的处理方法包括位移-压强混合格式、B-bar和F-bar 方法等[9].然而这些方法大多都用于静力问题的计算,而对于不可压材料的显式动力学模拟,目前相关的算法还比较少.此外,由于软材料在受外界刺激或载荷作用时可能会产生极端的大变形[10],采用FEM 进行模拟时可能会产生网格畸变,导致模拟结果的误差较大或者难以收敛,甚至可能模拟失败[11].因此,FEM 在模拟大变形动力学问题时仍然具有一定的局限性.

为了更准确、有效地模拟大变形动力学问题,Sulsky等[12-13]于1994 年将流体力学中的质点网格法加以改进,提出了一种新的粒子类方法,即物质点法(MPM).MPM 将求解对象离散成物质点并设置独立于物质点的背景网格,这种处理方式结合了拉格朗日和欧拉描述的优势,使其在避免FEM 中可能出现的网格畸变的同时也无需处理欧拉描述中的对流项.因此近年来被广泛应用于高速冲击[14]、裂纹扩展[15]、边坡失稳[16]等诸多大变形强非线性问题的模拟中.

然而,传统的MPM 在模拟大变形问题时物质点会跨越背景网格,其所采用的线性插值函数的梯度不连续性会产生较大的跨网格误差[17].为了提升MPM 的精度,众多学者对MPM 进行了一系列改进,提出了广义插值物质点法[18]、对流粒子域插值物质点法[19]和B 样条物质点法[20]等方法.de Vaucorbeil等[21]基于B 样条插值提出了一种完全拉格朗日物质点法TLMPM,可以很好地消除这一误差并减小计算量.该方法已经被成功应用于模拟大变形准静态[22]和动力冲击问题[23].

与FEM 类似,MPM 在计算不可压材料时同样会产生体积自锁,也需要进行特殊处理.Kularathna等[24]与Zhang等[25]将Chorin 提出的投影方法应用到MPM 中,用于求解不可压流体;Coombs等[26]将F-bar 方法扩展到MPM 中用于克服不可压材料中出现的体积自锁现象;Iaconeta等[27]提出了一种位移-压强混合格式的隐式MPM 用于求解不可压材料的准静态大变形行为.然而目前在求解不可压软材料的大变形动力学问题时,显式MPM 仍然缺乏有效的途径克服体积自锁.

本文在TLMPM 理论框架下,基于近似不可压软材料的体积应变能形式,通过引入压强控制方程并进行离散,提出一种位移-压强混合格式的显式TLMPM,用于稳定求解近似不可压软材料的大变形动力学问题.此外还给出了若干算例,以验证所提出算法的准确性和有效性.

1 TLMPM 基本理论

1.1 控制方程

对于大变形问题,其初始构型上坐标为X的点在变形后移动到位置x.可以据此计算变形梯度为

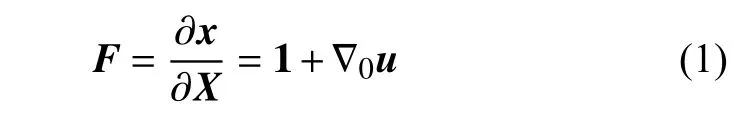
其中,1为2 阶单位张量,u=x-X表示位移,∇为梯度算子,下标0表示相对于初始构型的量.对于动力学问题,其拉格朗日格式的动量方程为[28]

其中,ρ为密度,ü 表示u对时间的2 阶导数,P为PK1 应力,b为体力.引入位移试函数wu并应用高斯散度定理,推导可得等效积分弱形式为

1.2 离散及变量更新

与在计算过程中不断更新构型的传统MPM 不同,TLMPM 在求解力学问题时不参考当前构型,而是将初始构型上的求解域离散成若干个物质点,离散后物体的质量、体积等属性集中在物质点上.同时在求解域范围内设置背景网格,于是背景网格的等效质量可以由物质点得到,即

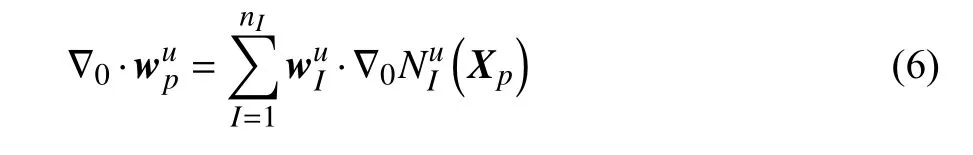
其中nI为背景网格节点的总数.类似地,位移、速度和加速度也同样可以采用类似的方法进行映射.

将插值映射格式带入弱形式方程(3),经整理可得每个节点的离散控制方程为

其中h0为边界层的厚度.

在时间积分方面,对于显式MPM,可以采用向前差分和中心差分两种格式[21,29].为了简便计算,考虑采用向前差分法进行积分,便可得到时间、空间离散后的TLMPM 离散求解格式,即

根据式(10)可以得到各个节点在t+Δt时刻的速度.而对于物质点上的变量,则需要根据节点上的变量进行逆映射,其具体形式为

2 位移-压强混合格式

2.1 压强控制方程及其离散

在对凝胶、生物材料等软材料进行数值求解时,由于其往往具有不可压特性,因此会产生体积自锁,对计算结果的精度造成很大影响.因此需要对当前的TLMPM 进行改进,以提升其精度.

在大变形框架下,近似不可压软材料的应变能密度可以写成[30-31]

其中C=FTF,Wdev和Wvol分别为应变能函数的偏量部分和体积部分.这里可以假设软材料符合Neo-Hookean 本构关系,其偏量应变能密度Wdev的形式为[9]

式中,µ为剪切模量,I1和I3分别为为C的第一和第三不变量.而对于近似不可压材料,Wvol可以取

其中,J=det(F),K为体积模量.

在采用TLMPM 求解时为了避免体积自锁,将应力分解成

其中p为静水压力.它与体积应变能存在如下关系

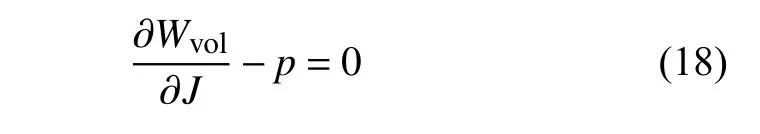
基于TLMPM 框架将该方程离散求解,便可对体应力进行修正以避免体积自锁,从而得到改进后的混合TLMPM 求解格式.为了离散方程(18),首先引入压强试函数wq以推导出它的弱形式

于是,物质点上的静水压力为

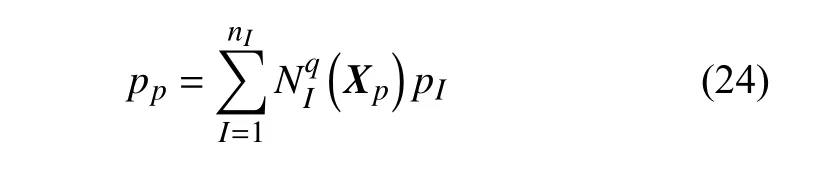
此外,为了满足混合格式中的LBB 条件[32]以保证算法的收敛性,需要考虑采用不同阶次的B 样条基函数分别对位移和压强进行插值.B 样条函数可以较为简单地实现高阶插值,并且易于改变插值的阶次,用其作为插值函数可以提升MPM 的精度,实现混合格式的物质点法时无需增加新的节点,程序实现较为简便[33].物质点法中具体的B 样条插值实施细节可以参考文献[20]的相关工作.在本文中,如无其他说明,位移和压强插值分别采用二次和线性B 样条插值,这种插值方法可以满足LBB 条件,保证算法的准确性和收敛性[34].

2.2 交错求解流程

为了同时考虑位移和压强场的求解,混合格式的TLMPM 采用交错求解的格式,在一个时间步内依次进行位移和压强场的求解,其流程如下.

(1) 位移场求解:

①将物质点的质量和体积映射到节点上;

②计算节点的内力、外力向量;

③求解位移场方程(7),更新节点速度;

④更新物质点速度、位移、变形梯度;

(2) 压强场求解:

①将体积变形重映射,计算物质点等效体积比;

②求解压强场方程(21),更新节点压强;

③更新物质点的压强;

(3) 应用本构关系,即式(17)更新应力.

3 数值算例

为了验证本文提出的针对近似不可压软材料动力学的完全拉格朗日物质点算法,本节给出了几个典型的数值算例.在各个算例的模拟中,为了消除时间步长对结果的影响,时间步长统一设置为

其中Δtcr为临界时间步长,其确定方法可以参考文献[17].

3.1 库克膜问题

首先考虑库克膜问题[34],该问题通常被用来验证算法处理体积自锁的能力.如图1 所示,模型左端固定,右端受到大小为0.25 N/m 的均匀剪力.模型采用近似不可压材料,其弹性模量和泊松比分别为1000Pa和0.499,密度为1 kg/m3.为了验证算法的网格收敛性,模拟时采用不同尺寸的背景网格并将模型离散成不同数量的物质点,初始时每个背景网格内包含4 个物质点,采用标准格式和混合格式的TLMPM 分别进行模拟,计算获得的t=3 s 时模型右上角点的竖直位移如图2 所示.可以看出标准的TLMPM 的模拟结果在物质点较密时逐渐趋近于混合格式的结果.图3 给出了两种算法在t=3 s 时的静水压力分布图,从图中可以看出混合格式的 TLMPM相比标准格式能得到更光滑的结果.这表明了本文提出的混合格式的TLMPM 可以更有效地避免体积自锁,得到更合理的应力结果.

图1 库克膜问题示意图(单位:mm)Fig.1 Schematic plot of Cook’s membrane(unit:m)

图2 库克膜:采用不同数量物质点离散的t=3 s 时右上角竖向位移模拟结果Fig.2 Cook’s membrane:simulation results of the vertical displacement of the top right corner at t=3 s using different numbers of material points

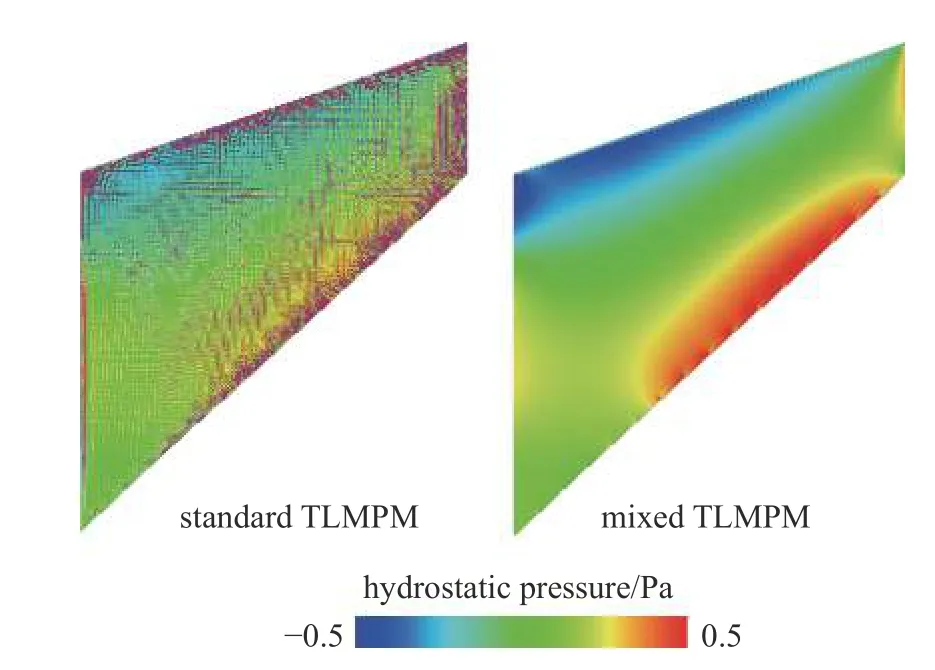
图3 库克膜:t=3 s 时的静水压力分布Fig.3 Cook’s membrane:hydrostatic pressure distribution at t=3 s

3.2 二维软梁的弯曲

考虑一个二维近似不可压软材料梁的大变形弯曲问题.模型的尺寸、边界条件如图4 所示,梁的下端固定,并整体给定初速度为10m/s.采用近似不可压Neo-Hookean 材料,对应的弹性模量和泊松比分别17 MPa和0.499,密度为1100kg/m3.将模型采用不同密度的背景网格进行离散,保持每个背景网格内包含4 个物质点,分别采用混合格式和标准格式的TLMPM 进行模拟并考虑不同阶次的插值函数,不同网格密度和插值函数的模拟结果分别如图5和图6 所示.图5(a)是不同网格尺寸的A点的位移时程曲线,表明了混合格式的 TLMPM 相比标准TLMPM收敛性更好.对于网格尺寸为0.1 m 的模型,将插值函数的阶次降低,分别得到线性位移插值的混合格式的 TLMPM和标准TLMPM 模拟结果与之前的模拟进行对比,其中线性位移插值的混合格式的TLMPM为满足LBB 条件压强采用0阶插值.结果如图5(b)所示,从图中可以看出混合格式的TLMPM即使降低了插值阶次仍然可以得到和二次位移插值较为相似的结果,而线性插值的标准TLMPM 结果与其他的相差较大.表明了混合格式的 TLMPM 在进行近似不可压软材料的大变形问题的模拟时比标准TLMPM 具有更好的效果.

图4 二维软梁的弯曲问题示意图Fig.4 Schematic plot of bending of 2D soft beam

图5 二维软梁的弯曲:A点x 方向位移变化曲线Fig.5 Bending of 2D soft beam:history curves of x-displacement of point A

分别提取了4 次模拟在t=0.5,1.0s 的静水压力分布,如图6 所示,可以看出线性的标准TLMPM的构型与其他3 种相差较大并且无法计算出合理的静水压力,而混合格式 TLMPM 在对近似不可压材料的体应力计算上可以得到理想的结果.

图6 二维软梁的弯曲:不同时刻的静水压力分布.(a)～(b) 标准格式线性插值;(c)～(d) 标准格式二次插值;(e)～(f) 线性-常数混合格式;(g)～(h) 二次-线性混合Fig.6 Bending of 2D soft beam:hydrostatic distribution at different times.(a)～(b) Standard linear interpolation;(c)～(d) standard quadratic interpolation;(e)～(f) linear-constant mixed formulation and(g)～(h) quadratic-linear mixed formulation

3.3 三维柱体扭转

最后,考虑一个三维柱体的扭转问题.一个方形截面柱底端受约束,整个柱体受到与其坐标相关的初速度而发生扭转,其构型如图7(a)所示,柱体尺寸为1 m×1 m×6 m,底面固定,将坐标原点取在底面中心,给柱体施加与位置坐标相关的初速度为:vx=-ysin(πz/12),vy=xsin(πz/12).材料参数与3.2 节的二维软梁相同.将模型离散成20×20×120个物质点,并设置网格尺寸为0.1 m,即模型内部的每个背景网格内有8 个物质点.采用标准和混合格式的TLMPM 进行模拟,得到0.1 s和0.3 s 的静水压力分布如图7(b)～图7(e) 所示.从图中可以看出,混合TLMPM 在模拟三维大变形问题时,静水压力结果在网格内和网格之间仍然只有很小的振荡,而标准的TLMPM 则受体积自锁影响,无法得到合理的静水压力结果.同时,得到A点的z方向位移时程曲线如图8 所示,同时考虑了混合格式的传统MPM,并将结果与改进单元技术的混合格式FEM 结果[30]进行对比,可以发现混合格式的TLMPM 与FEM 的结果相差很小,而标准TLMPM和混合格式的MPM的结果与它们有一定差距.

图7 三维柱体扭转:构型及静水压力分布.(a) 几何模型;(b) t=0.1 s,标准TLMPM;(c) t=0.3 s,标准TLMPM;(d) t=0.1 s,混合TLMPM;(e) t=0.3 s,混合 TLMPMFig.7 Twisting of a 3D column:configurations and distribution of hydrostatic pressure.(a) Geometry;(b) t=0.1 s,standard TLMPM;(c) t=0.3 s,standard TLMPM;(d) t=0.1 s,mixed TLMPM and(e) t=0.3 s,mixed TLMPM

图8 三维柱体扭转:A点z 方向位移变化曲线(参考解为文献[30]的计算结果)Fig.8 Twisting of a 3D column:history curves of z-displacement of point A(the reference results refer to Ref.[30])

通过以上几个算例,证明本文所提出的位移-压强混合格式的TLMPM 算法在模拟近似不可压软材料的大变形动力学问题时可以有效防止体积自锁,具有很好的收敛性和准确性.

4 结论

本文基于MPM 算法框架,发展了一种位移-压强混合格式的完全拉格朗日物质点法(TLMPM)用于模拟近似不可压材料软材料的大变形动力学问题.该方法通过体积应变能引入了关于静水压力的控制方程;进一步基于MPM 进行离散并采用完全拉格朗日格式以避免大变形问题中物质点跨网格所产生的误差;对位移场和压强场进行交错求解,并采用不同阶次的B 样条基函数对位移和压强分别进行插值.除此之外,还针对体积变形引入重映射技术以保证静水压力求解的准确性.通过几个二维和三维近似不可压问题的模拟,验证了本文提出的混合格式的TLMPM 可以有效避免体积自锁,具有很好的收敛性并能够得到光滑的应力结果,在模拟软材料大变形动力行为时效果相比标准TLMPM和混合格式的MPM 都更为有效.