基于多目标驱动的风管机电机支架优化设计
2023-01-15陈国平陈澎钰张进男张旭
陈国平 陈澎钰 张进男 张旭
1.海信家电集团有限公司 山东青岛 266100;
2.海信(山东)空调有限公司 山东青岛 266100
0 引言
风管机因具有制热量高、不占空间、安装美观等优点,已逐渐代替挂壁式空调及柜式空调走进消费者家中。但相较于壁挂式空调,风管机噪声太大,易导致用户投诉。因此对风管机进行减振降噪势在必行。在实际研究中发现,风管机噪声主要来源于电机的运转[1]。电机固定在电机支架上,电机轴安装有离心风扇做高速旋转,若电机支架的刚度不足引发变形,则会导致整个系统的剧烈振动,引起更大的噪声,所以对电机支架的刚度进行优化显得尤为重要。
响应面优化的分析方法采用多元二次回归方程来拟合变量与目标函数之间的关系。当存在两个以上变量时,输入结果以三维空间中的曲面表现[2-4]。响应面法在结构优化设计、参数优化方面有着绝对的优势。目前国内外学者利用响应面法进行了大量结构优化的研究。李伟[5]等针对变速箱壳体进行轻量化设计,以模型质量、变形、应力为优化目标,在应力和变形基本不变的前提下,对变速箱的壳体进行减薄设计。吕雷雷[6]等针对影响冷加工工艺的参数进行优化,对冲压速度、摩擦系数、冲头凸台斜角以及冲头凸台长度进行分析,得出一组加工效果最好的解。史尧臣[7]等针对精密同步带齿形测量装置的带轮轴进行分析,以滑动带轮轴的最大变形为目标函数,分析了滑动端轴长度及轴直径对最大变形的影响。
国内将响应面法应用于空调器领域的研究不多,国外学者主要应用响应面的理论对空调的性能进行优化[8-12]。Yiwei Xie[8]等将优化思想应用到地源热泵的参数协同上,在保证室内温度舒适的同时,在最大限度地提高系统性能和降低运行成本的前提下,找到最优的设计点组合。Se Min Park[9]等利用响应面优化进行空调室外机组的减振降噪研究,利用响应面法对风机孔板进气半径、孔板颈部长度、孔板出口角度三个几何参数进行了优化设计,提取最佳参数组进行验证,结果表明,优化后的参数在相同运行转速下,流量提高了2.1%,噪声降低了2.8 dB(A),功耗降低了4.0%。
本文针对风管机的电机支架进行优化设计,首先进行静力学分析,确定危险点的位置及影响因素;然后定义电机支架的结构参数为输入变量,定义最大应力、最大应变以及电机支架的质量为输出变量,通过灵敏度分析得到输入变量与输出变量之间的关系;最后通过设定优化目标,得到优化后的电机支架结构参数;通过优化前后输出结果的对比,得出对电机支架优化的可靠性。
1 静力学分析
静力学分析是有限元分析最基本、最常用的一个领域,一般分析结构的位移、应力及应变。在经典力学理论中,物体的动力学通用方程为:
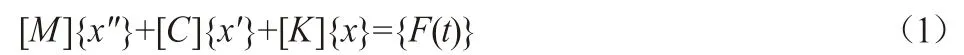
式中:[M]-质量矩阵;[C]-阻尼矩阵;[K]-刚度矩阵;{x}-位移矢量;{F(t)}-力矢量。
1.1 有限元模型的建立
本文针对某品牌F5D风管机空调的电机支架进行分析,结构如图1所示。主要由面板、电机轴、电机、电机支架、风扇蜗壳组成。离心风扇安装在电机轴上,隐藏在风扇蜗壳中。电机支架通过螺栓固定在面板上,电机通过卡钩固定在电机支架上。

图1 电机支架位置示意图
常用电机支架材料为304不锈钢,材料属性如表1所示,在ANSYS中完成对电机支架材料的属性设置。将带有参数的电机支架模型导入有限元分析软件后,对模型进行四面体网格划分,划分后的网格共有176199个单元,619757个节点,如图2所示。

表1 材料属性
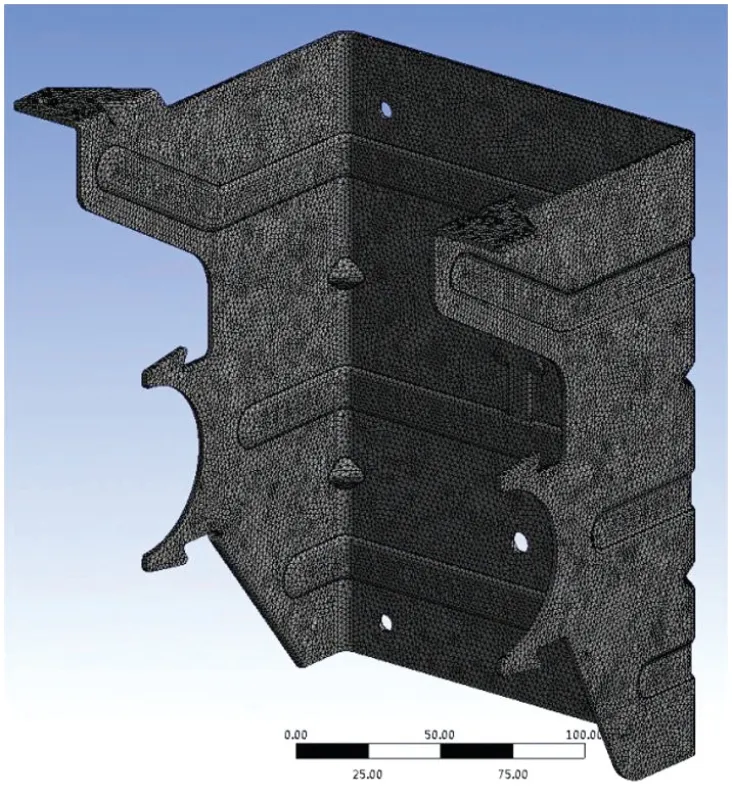
图2 网格划分
1.2 电机支架静力学分析
对电机支架进行静力学分析,在模拟工况的条件下,对电机支架背面施加固定约束,模拟电机支架固定在面板上;对电机支架的吊耳施加固定约束,模拟支架固定在顶板上。电机质量为6.11 kg,两个离心风扇质量为1.94 kg,固定卡钩部件的质量为0.28 kg。故向下施加85 N的均布力模拟电机、风扇对支架的压力。得到电机支架的应力和变形结果如图3所示。可以看出电机支架的最大应力集中在支架与卡钩接触的圆角处,最大应力为6.014 MPa;最大变形集中在固定电机圆环的上下边位置,最大变形为0.003 mm。
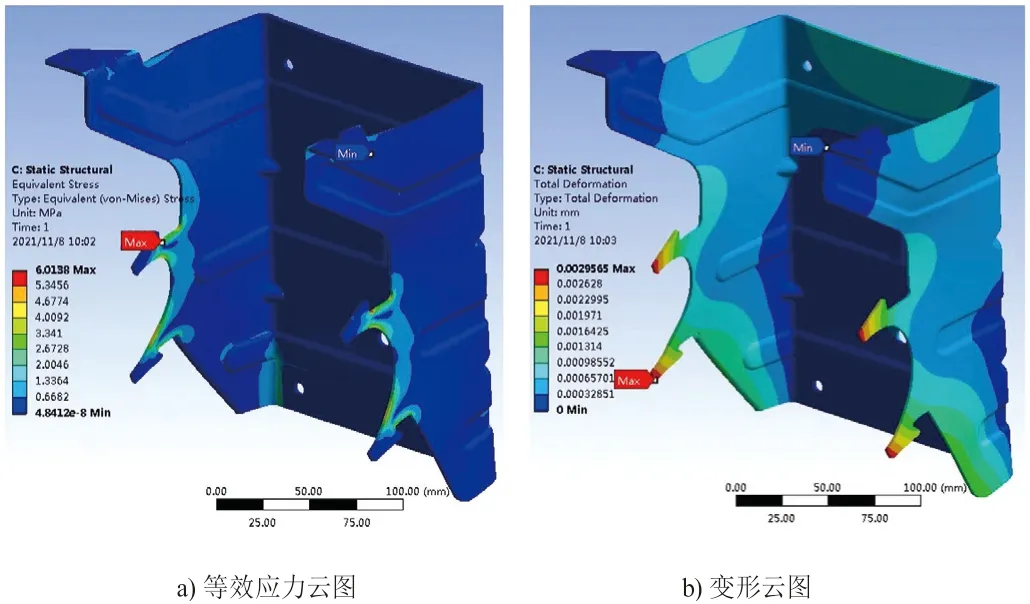
图3 电机支架静力学分析结果
2 响应面优化
响应面优化分析是通过对输入参数采用回归分析的方法拟合成与输出参数成一定关系的曲面,得到输入参数与输出参数之间的关系。响应面模型如下:
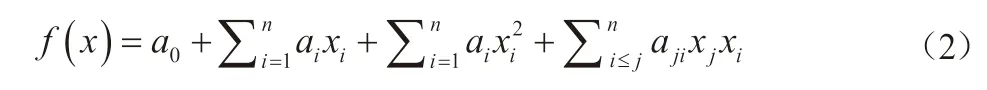
式中:a0、ai、aji为待定系数,输入数据为(x1……xn),输出数据g1(x1……xn),其中i等于1,2,……,k,xij为第i组数据中的第j个数据,可得矩阵如下:

2.1 参数灵敏度分析
灵敏度分析是通过统计学方法对输入参数与输出参数之间的关系进行分析,根据计算得到各个输入参数对输出参数的影响规律,设置对输出参数影响较大的输入参数为优化参数。设置电机支架的最大应力、最大变形、电机支架的质量为输出变量。本文共对电机支架的12个参数进行了变量输入,如图4所示。每个输入变量对结果的影响不同。故在进行响应面优化前对输入变量进行灵敏度分析,得到各输入变量对输出变量的影响。输入变量与输出变量之间的灵敏度关系如图5所示,图中横坐标为输出参数,包括质量、最大总变形、最大等效应力,纵坐标为参数敏感度。由图5可以看出:输入变量DS_1、DS_3、DS_6对电机支架质量的影响均为正值,且相关性系数大于10%,说明这三个参数对质量的关系为正相关,且对质量影响较大;输入变量DS_2、DS_7、DS_12对电机支架质量的影响均为负值,且相关性系数大于10%,说明这三个参数对质量的关系为负相关。其余参数对质量影响不大。同理DS_7、DS_12对电机支架最大变形的关系为正相关,DS_7对电机支架最大应力的关系为正相关。故本文将DS_1、DS_2、DS_3、DS_6、DS_7、DS_12这6个尺寸设置为优化参数。
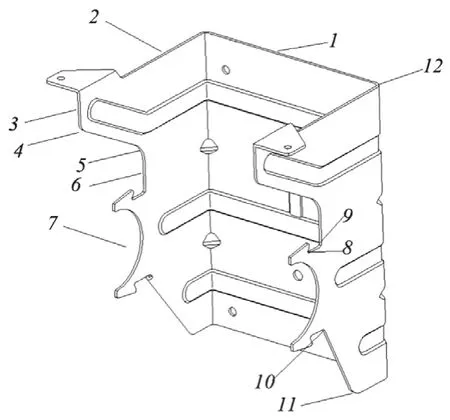
1-背板宽度;2-横梁长度;3-第一竖板长度;4-第一竖板圆角;5-第二竖板圆角;6-第二竖板长度;7-固定电机圆直径;8-第三圆角;9-第四圆角;10-固定支架圆角;11-底边圆角;12-竖板圆角
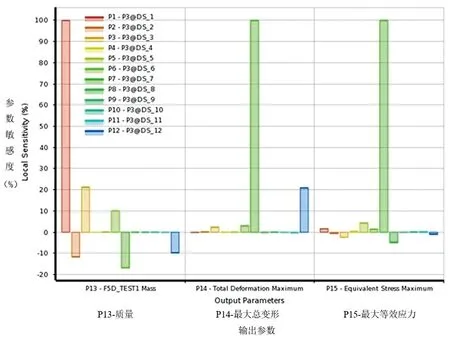
图5 输入变量与输出变量的灵敏度
2.2 响应面分析结果
根据对输入参数的灵敏度分析可知,对质量影响较大的参数有:DS_1、DS_2、DS_3、DS_6、DS_7、DS_12;对最大变形影响较大的参数有:DS_7、DS_12;对最大应力影响较大的参数有:DS_7。故针对6个输入参数进行优化。搭建Response Surface Optimization优化系统如图6所示。在DOE(Design of Experiments,实验设计方法)中建立一系列的取值点,通过拟合观察取值点的精度是否满足需求。选择Optinal Space-Filling Design的设计方式。生成样本数量为282,输入参数的变化范围为±10%。
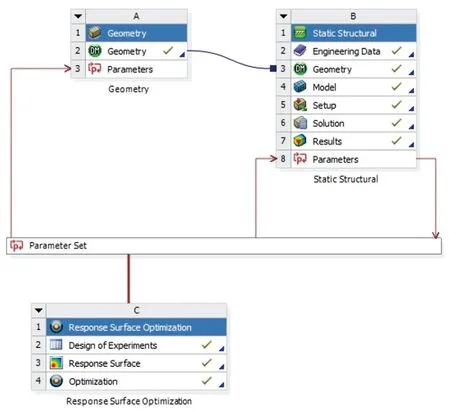
图6 响应面优化系统
由图7可以看出:各样本点对输入参数的拟合度较好,可以满足优化需求。因此可以通过观察响应面来具体分析各参数对输出变量的影响情况。各参数对最大变形的响应面如图8所示,对最大应力的响应面如图9所示,对支架质量的响应面如图10所示。可以看出,响应面的连续性、平滑性较好,可以满足优化需求。

图7 响应面优化参数拟合度
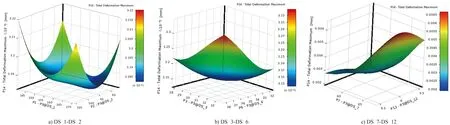
图8 最大变形的响应面云图
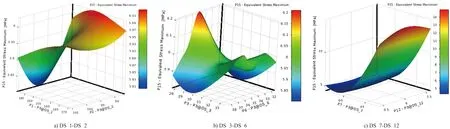
图9 最大应力的响应面云图
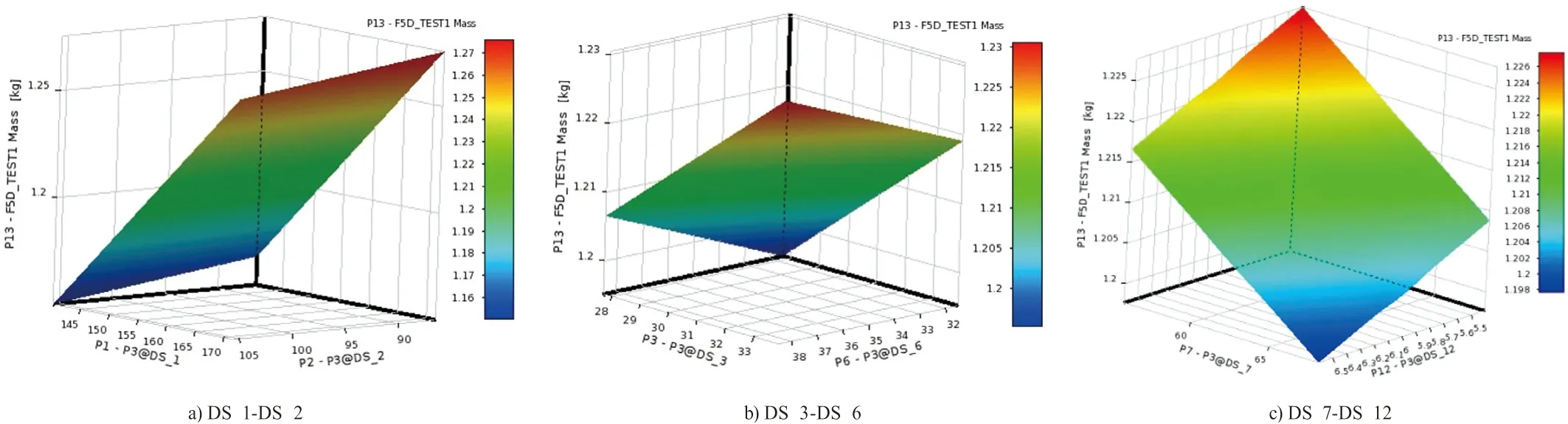
图10 支架质量的响应面云图
2.3 确定优化目标
输入参数的变化范围为±10%,故各参数的取值范围见表2,优化参数的取值范围如公式(7)所示。本文优化的目标是减轻电机支架的重量,同时强度仍能满足要求,故电机支架的最大应力和最大变形要分别小于静力学分析得到的数值,故优化目标如公式(8)所示。
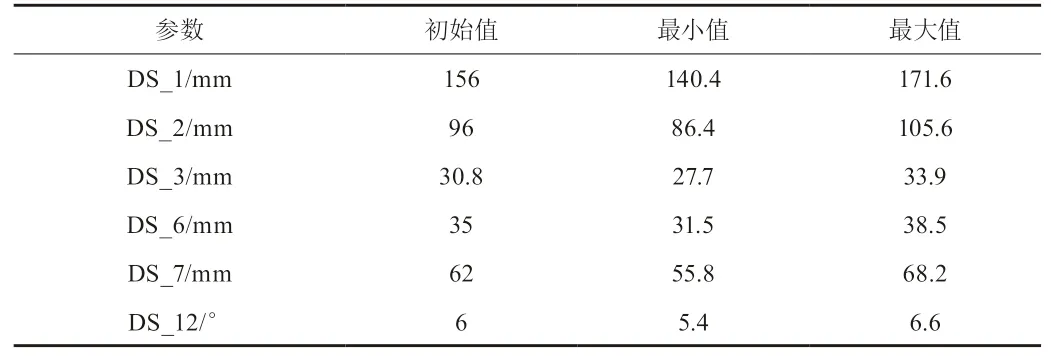
表2 优化尺寸变化范围

根据公式(8)设置目标和约束,设置3个候选点,优化后给出的3组优化方案如表3所示。对比给出的三组优化方案发现方案B的等效应力和变形最小,轻量化程度最高,故针对方案B给出的优化尺寸进行参数取整,按DS_1=151.5 mm,DS_2=97.5 mm,DS_3=30.1 mm,DS_6=34 mm,DS_7=61 mm,DS_12=5.5°进行重新建模与求解,得到优化后的电机支架静力学分析结果如图11所示。可以看出:最大应力集中在支架与卡钩接触的圆角处,最大应力为5.58 Mpa;最大变形集中在固定电机圆环的上下边位置,最大变形为0.0028 mm。与优化前的静力学结果相比,优化后的结构应力集中和最大变形的位置没有发生变化,但优化后的最大应力减小了7.3%,最大变形减小了6.7%,质量减轻了8.1%,做到轻量化的同时,电机支架的强度和可靠性得到了明显的提升。

图11 优化后的电机支架静力学分析结果

表3 优化方案对比
3 实验验证
为了验证优化方案的准确性,按2.3小节中优化方案B给出的结构尺寸制作电机支架的手板样件。根据胡克定律:在一定的比例极限范围内应力与应变成线性比例关系,故采用应变片分别测试原方案电机支架与优化方案电机支架的应变情况。测试结果为:原方案电机支架的应变为127 με,最大应变发生在支架与卡钩接触的圆角处;优化方案电机支架的应变为112 με,最大应变也发生在支架与卡钩接触的圆角处。实验结果表明:优化后的电机支架应变改善了11.8%,最大应变的位置没有改变。实验与仿真的对比结果为:最大应变发生位置与仿真结果一致,优化后的电机支架力学性能的确得到了提升,能够在一定程度上验证仿真分析结果的准确性。
4 总结与讨论
本文以风管机电机支架为研究对象,针对影响电机支架力学性能的结构参数进行分析,得到以下结论:
(1)影响电机支架最大应力和最大变形的主要因素为固定电机的圆环直径DS_7,且对应力、应变均为正向影响,对质量为负向影响。
(2)对电机支架结构参数优化,更改背板宽度为151.5 mm、横梁长度为97.5 mm、第一竖板长度为30.1 mm、第二竖板长度为34 mm、固定电机圆直径为61 mm,竖板圆角为5.5°,结构最大变形减小了6.7%,最大应力减小了7.3%,质量减轻了8.1%。优化后电机支架的强度和刚度均明显增强,电机支架的结构可靠性得到提升。
(3)利用响应面的方法进行结构优化,缩短了设计周期,降低开发费用,为结构件的优化设计提供了方法。
(4)文中对电机支架网格的划分、约束的施加方式、边界条件的设置等是否合理,以及优化设计模型的可靠性还需进一步实验验证。
